Цель работы: показать важную, исключительную роль принципа симметрии в научном познании мира и в человеческом творчестве.
Задачи: рассмотреть основные виды симметрии, показать связь между математикой, природой, искусством, научить различать многообразные проявления симметрии в окружающем мире; изучить научно-популярную литературу, исследовать проявление симметрии в различных науках, показать применение симметрии в решении задач. Обобщить материал в виде презентации для последующего использования на уроках математики и во внеурочной работе.
Гипотеза: в любой науке есть симметрия.
Если бы все окружающее обладало симметрией - мир был бы совершененным.
Методы: 1.Исследовательский метод изучения литературы, интернет - ресурсов и его анализ.
2. Наблюдение для выяснения, где используется симметрия, в каких науках применяется, какие из фигур и графиков имеют симметрию.
3.Прикладной метод. Показать применение симметричности в решении задач.
Практическое значение работы: создание презентации и подборка задач, решаемых с применением симметрии.
Этапы выполнения работы: на первом этапе выполнения работы выбрана тема, составлен список литературы, определены предметы изучения и проанализированы. На втором этапе при изучении литературы, интернет - ресурсов были определены виды симметрии, области наук, где используется симметрия. Наблюдал проявления симметрии в окружающем мире. На третьем этапе использован метод практического применения симметрии в решении задач.
Ожидаемые результаты: В процессе изучения расширяются и углубляются знания, формируются практические умения и навыки.
Введение.
“Симметрия является той идеей, посредством которой, человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство» (Г.Вейль)
Мир наш исполнен симметрии. С древнейших времен с ней связаны наши представления о красоте. Наверное, этим объясняется непроходящий интерес множества выдающихся мыслителей от Платона и Евклида до Эйлера и Коши. Наверное, каждый человек не раз задумывался над вопросом, почему природа способна создавать такие удивительные гармоничные структуры, восхищающие и радующие глаз. Почему художники, поэты, композиторы, архитекторы создают произведения искусства, остающиеся шедеврами из века в век? Попытаемся ответить на этот вопрос. Да, верно, но прошло много веков, прежде чем это понятие сформировалось.
С симметрией мы встречаемся везде: в природе, технике, искусстве, науке. Отметим, например, симметрию, свойственную бабочке и кленовому листу, симметрию форм автомобиля и самолета, симметрию в ритмическом построении стихотворения и музыкальной фразы, симметрию атомной структуры молекул и кристаллов.
Симметрия - закономерное расположение элементов формы относительно плоскости, оси или точки. Человек давно осмыслил симметрию в творениях природы и стал использовать её как средство организации искусственных форм. В Древней Греции слово "симметрия" было синонимом красоты, гармонии формы. Термин “симметрия” по-гречески означает “соразмерность, пропорциональность, одинаковость в расположении частейования.
Симметрия-это способ создания красоты. Симметрия пронизывает буквально все вокруг, захватывая, казалось бы, совершенно неожиданные области и объекты. Здесь уместно привести высказывание Дж. Ньюмена, который особенно удачно подчеркнул всеохватывающие и вездесущие проявления симметрии: «Симметрия устанавливает забавное и удивительное сродство между предметами, явлениями и теориями, внешне, казалось бы, ничем не связанными. Что же это за мир – мир симметрии? Это мир вокруг нас. Это особенно актуально, так как часто математика воспринимается учащимися как трудный предмет, оторванный от окружающих явлений. При рассмотрении темы «Симметрия» формируются не только математические
знания, но и расширяется кругозор, формируется эстетический вкус. Данная работа может послужить для учащихся толчком к самостоятельному изучению различных явлений и процессов, связанных с симметрией и может стать началом исследовательской работы.
В этом проекте я расширю представления о симметрии, научу различать многообразные проявления симметрии в окружающем мире; покажу важную, исключительную роль принципа симметрии в научном познании мира и в человеческом творчестве, покажу результаты исследования и проявления симметрии в различных науках, в решении задач. Но рассказать обо всем у меня не получится, так как этот мир невероятно велик.
Симметрия вокруг нас.
Обратимся к истории. Первые представления о симметрии идут к нам из глубины веков. Так, например, древнегреческий философ Платон говорил «Упорядочение целого есть превращение целого в гармонию, а определенное строение гармонии есть симметрия, пропорция, ритм». Платон считал симметрию одним из элементов гармонии. Да действительно, симметричные объекты часто выделяют как красивые, гармоничные.
Симметрия во все времена интересовала людей, причём не только математиков. Например, Л. Н. Толстой говорил: «Стоя перед черной доской и рисуя на ней мелом разные фигуры, я вдруг был поражен мыслью: почему симметрия понятна глазу? Что такое симметрия? Это врожденное чувство, отвечал я сам себе. На чем же оно основано?”. Действительно симметричность приятна глазу. Кто не любовался симметричностью творений природы: листьями, цветами, птицами, животными. Или творениями человека: зданиями, техникой, – всем тем, что нас с детства окружает, тем, что стремится к красоте и гармонии. Что же это симметрия?
Даль: Симметрия - соразмер, соразмерность, равно (или разно) подобие, равномерие, равнообразие, соответствие, сходность; одинаковость, либо соразмерное подобие расположения частей целого, двух…
Брокгауз: Симметрия - это такое расположение частей предмета или организма, при котором по обе стороны срединной линии все части представляют полное и точное повторение.
Википедия: Симметрия - соответствие, неизменность (инвариантность), проявляемые при каких-либо изменениях, преобразованиях (например: положения, энергии, информации, другого).
Математически строгое понятие симметрии сформировалось недавно – в 19 веке немецким математиком Германом Вейлем. По Г.Вейлю симметрия - это идея, с помощью которой человек веками пытался объяснить и создать порядок, красоту и совершенство. Всякий раз, когда мы, говорим о гармонии, красоте, эмоциональности воздействуя, мы тем самым касаемся симметрии.
Но для того, что бы таким образом изменять объекты, надо знать, как это делать. Несмотря на кажущуюся простоту формулировки в сочетании с современными теориями физики, химии и других естественных наук, а также новыми открытиями (например нейтрино) в этих областях симметрия пространства становится всё более запутанной. Но несомненно одно: Мир симметричен.
Виды симметрии.
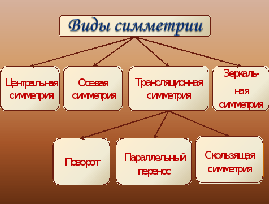
1.Осевая симметрия — тип симметрии, имеющий несколько отличающихся определений:
Отражательная симметрия. В евклидовой геометрии осевая симметрия — вид движения (зеркального отражения), при котором множеством неподвижных точек является прямая, называемая осью симметрии. Отсюда следует, что любой точке соответствует точка, находящаяся на том же расстоянии от оси симметрии, и лежащая на одной прямой с исходной точкой и их общей проекцией на ось симметрии. Например, плоская фигура прямоугольник в пространстве осесимметрична и имеет 3 оси симметрии (две — в плоскости фигуры), если это не квадрат, а параллелограмм общего вида имеет одну ось симметрии (перпендикулярно плоскости).
Вращательная симметрия. В естественных науках под осевой симметрией понимают вращательную симметрию (другие термины — радиальная, аксиальная, лучевая симметрии) относительно поворотов вокруг прямой. При этом тело (фигуру, задачу, организм) называют осесимметричными, если они переходят в себя при любом (например, малом) повороте вокруг этой прямой. В этом случае, прямоугольник не будет осесимметричным телом, но, например, треугольник будет.
2.Центральной симметрией (иногда центральной инверсией) относительно точки A называют преобразование пространства, переводящее точку X в такую точку X′, что A — середина отрезка XX′. Центральную симметрию можно перепутать с осевой симметрией. Другое названия этого преобразования — симметрия с центром A. Центральная симметрия в планиметрии является частным случаем поворота, точнее, является поворотом на 180 градусов.
3.Трансляционная симметрия — тип симметрии, при которой свойства рассматриваемой системы не изменяются при сдвиге на определённый вектор, который называется вектором трансляции. Например, однородная среда совмещается сама с собой при сдвиге на любой вектор, поэтому для неё свойственна трансляционная симметрия.
Трансляционная симметрия свойственна также для кристаллов. В этом случае векторы трансляции не произвольны, хотя их существует бесконечное число. Среди всех векторов трансляций кристаллической решётки можно выбрать 3 линейно независимых таким образом, что любой другой вектор трансляции был бы целочисленно-линейной комбинацией этих трёх векторов. Эти три вектора составляют базис кристаллической решётки.
4.Зеркальная симметрия — Оптическое отражение в луже гаражей и соседнего жилого дома Отражение, зеркальное отражение или зеркальная симметрия движение евклидова пространства, множество неподвижных точек которого является гиперплоскостью (в случае трехмерного пространства …
Фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре. Точка О называется центром симметрии фигуры. Говорят также, что фигура обладает центральной симметрией. Центр симметрии у фигур один. (Слайд)
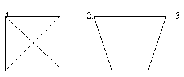
Фигура называется симметричной относительно прямой, если эта прямая делит эту фигуру на две равные части совпадающие при перегибании по этой прямой I (I – ось симметрии)
Например: А и В симметричны относительно прямой I.
а) АВ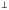 
I; б) АО=ОВ
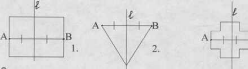
Ось симметрии и плоскость симметрии могут быть несколько. Бесконечное число плоскостей симметрии имеет шар, круговой цилиндр, круговой конус, и т.д.
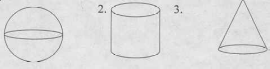
Правильный шестиугольник имеет 6 осей симметрии, круг множество осей симметрии.
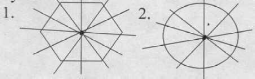
Примером зеркально симметричных объектов являются: а) одномерный объект ( О - центр симметрии) рис 1, б) двухмерный объект (I – ось симметрии) рис.2. в) трехмерный объект (a - плоскость симметрии) рис 3.
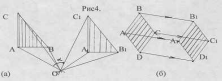
Приведем примеры поворотной симметрии рис.4(а) и параллельный перенос 4(б).
Зеркальная симметрия
Зеркальная симметрия- это симметрия окружающего нас мира. Построение изображения с помощью зеркальной симметрии сходно с отражением в зеркале.
Порассуждаем о зеркальной симметрии. Легко установить, что каждая симметричная плоская фигура может быть с помощью зеркала совмещена сама с собой. Достойно удивления, что такие сложные фигуры, как пятиконечная звезда или равносторонний пятиугольник, тоже симметричны. Как это вытекает из числа осей, они отличаются именно высокой симметрией. И наоборот: не так просто понять, почему такая, казалось бы, правильная фигура, как косоугольный параллелограмм, несимметрична. Несимметрична и спираль.
В то время как симметричные фигуры полностью соответствуют своему отражению, несимметричные отличны от него: из спирали, закручивающейся справа налево, в зеркале получится спираль, закручивающаяся слева направо
В трехмерном мире пространственных тел, где мы с вами живем, существуют плоскости симметрии. «Зеркало» всегда имеет на одно измерение меньше, чем мир, который оно отражает. При взгляде на круглые тела сразу видно, что они имеют плоскости симметрии, но вот сколько именно — решить не всегда просто.
Более двух тысячелетий традиционно отдается предпочтение геометрическим телам.
Из четырех правильных (равносторонних) треугольников получается тетраэдр (четырехгранник). Из восьми правильных треугольников можно построить октаэдр (восьмигранник) и, наконец, из двадцати правильных треугольников — икосаэдр. И только из четырех, восьми или двадцати одинаковых треугольников можно получить объемное геометрическое тело.
Конечно, все мы знаем, как отражает зеркало, но, если только потребуется описать это точно, несомненно возникнут трудности. Каждый ребенок, исполненный удивления перед окружающим миром, непременно заинтересуется, каким образом зеркало отражает его. Но взрослые обычно отвечают в подобных случаях: «Не задавай глупых вопросов!» Человек сникает, начинает стесняться, удивление его постепенно затухает, и он старается больше не проявлять его до конца жизни
Но вспомним о словах Бертольда Бреста: «Глупых вопросов не бывает, бывают только глупые ответы».
Закон отражения Снеллиуса объясняет явление зеркального отражения.
Каждой точке предмета соответствует её отражение в зеркале, и потому в нём наш правый глаз перемещается на левую сторону. Вследствие этого переноса точек предметы, расположенные дальше, в зеркале тоже кажутся уменьшенными в соответствии с законами перспективы...
В нём найдены в принципе зеркальное соответствие каждому изображению.
Симметрия в архитектуре.
Особенно блистательно использовали симметрию в архитектурных сооружениях древние зодчие. Древнегреческие архитекторы были убеждены, что в своих произведениях они руководствуются законами, которые управляют природой. Выбирая симметричные формы, художник тем самым выражал свое понимание природной гармонии как устойчивости, спокойствия и равновесия.
Стремление к красоте заложено в человеке природой. Наверное, поэтому человеческое творчество во всех своих проявлениях тяготеет к симметрии. Да архитектурные сооружения, построенные на законах симметрии, вызывают восхищение. (Слайд). А какие чувства испытываете вы, глядя на архитектурные здания, построенные на законах симметрии? (Спокойствие, умиротворение, близость с прекрасным, порядок). И это не случайно. Вот как обосновывает проявление этих чувств известный французский архитектор Ле Корбюзье, в своей книге «Архитектура 20 века»: «Человеку необходим порядок: без него все его действия теряют согласованность, логическую взаимосвязь. Чем совершеннее порядок, тем спокойнее и увереннее чувствует себя человек. Он делает умозрительные построения, основываясь на порядке, который продиктован ему потребностями его психики, - это творческий процесс. Творчество – есть акт упорядочения».
Глядя на эти величественные здания, хочется создать что-то красивое своими руками. Но, наверное, нам это не под силу. Нам не под силу построить архитектурный шедевр, но мы можем творить красоту своими руками в другом направлении – декоративно прикладном творчестве. (Слайд № 11). Вязаные салфетки, орнаменты на коврах, посуде и одежде, бордюры содержат элементы симметрии. В разные времена, у разных народов были свои особенности орнаментов. Поэтому по орнаменту можно определить время и страну, к которой относится изделие с орнаментом.
В современном мире тоже используют орнаменты для украшения интерьера: обои, салфетки, ковры, паркет и т.д. Для экстерьера - изделия из дерева с резьбой, металлические кованые предметы, бордюры. Во все времена человек стремился украсить своё жилище, а использование симметричных предметов и сейчас служит символом защиты домашнего очага от зла.
Тадж-Махал — мавзолей-мечеть, находящийся в Агре, Индия, на берегу реки Ямуна. Усыпальница имеет центральную симметрию относительно гробницы Мумтаз-Махал. Единственным нарушением этой симметрии является гробница Шах-Джахана, которую там соорудили после его смерти.
Симметрия в природе, физике.
Наверное, неслучайно безжизненный замок Снежной королевы из известной сказки Андерсона часто изображают как высшей степени симметричное сооружение. Каждая снежинка – это маленький кристалл замерзшей воды. Форма снежинок может быть очень разнообразной, но все они обладают симметрией, поворотной симметрией 6-го порядка и зеркальной симметрией.
Рис. 8. 
Камни, лежащие у подножия горы весьма беспорядочны, однако каждый камень является огромной колонией кристаллов, которые представляют собой в высшей степени симметричные постройки из атомов и молекул. Именно кристаллы вносят в мир неживой природы очарование симметрии. Кто из вас не любовался снежинками? Все твердые тела состоят из кристаллов. На рис №9 представлены кристаллы топаза, берилла, дымчатого кварца.
рис. 9.
Симметрия внешней формы кристаллов хорошо видна на рис 10, где показаны кристаллы каменной соли (а), кварца (б), арагонита ( в).
рис. 10
А на рис. 11 изображены три формы кристаллов алмаза: (а) октаэдр, (б) ромбический додекаэдр, (в) гексагональной октаэдр.
рис. 11
Вывод: Симметрия внешней формы кристалла является следствием его внутренней симметрии – упорядоченного взаимного расположения в пространстве атомов (молекул).
Иначе говоря, симметрия кристалла связана с существованием пространственной решетки из атомов так называемой кристаллической решетки.
Симметрия в быту.
(Слайд)
Симметрия в живописи.
Рис. 7.
На рисунках 1-7 хорошо видна симметрия.
Симметрия в музыке.
Душа музыки, ритм, состоит в правильном периодическом повторении частей музыкального произведения. Правильное повторение одинаковых частей в целом и составляет сущность музыки. Мы с большим правом можем приложить к музыкальному произведению понятие симметрии, что это произведение записывается при помощи нот. Самое непосредственное отношение имеет к симметрии композиция. Великий немецкий поэт И.В.Гете утверждал, что «Всякая композиция основана на скрытой симметрии. Владеть законами композиции – это значит владеть законами симметрии”.
Если взять простой пример: Песня “Песенка белочки” из музыкальной сказки “Дважды два-четыре”.
Каждый день без всякой спешки
Я в дупле грызу орешки:
Щелк-щелк-щелк
Щелк-щелк-щелк
Припев:
Я печальной не бываю,
Веселюсь и напеваю:
Ля-ля-ля
Ля-ля-ля
Всем видна моя сноровка,
Я скачу по веткам ловко
Скок-скок-скок
Скок-скок-скок
Припев:
Очень рыжая как осень,
Я мелькаю между сосен:
Прык-прык-прык
Прык-прык-прык.
Припев:
В этой песне чередуется куплет припев. Симметрию можно увидеть в стихотворениях – это чередование рифм, ударных слогов, т.е. ритмичность.
Например:
А.С. Пушкин.
В этот год осенняя погода
Стояла долго на дворе
Зимы ждала, ждала природа
Снег выпал только в январе.
Чередование рифм и чтение по интонации дает чувствовать прелесть (симметрии) Пушкинского стихотворения.
Симметрия в буквах
А; Д; Л; М; П; ; Ф; Ш. (вертикальная ось симметрии)
В; Е; З; К; С; Э; Ю. (горизонтальная ось симметрии)
Ж; Н; О; Х. (и вертикальные и горизонтальные оси симметрии)
Симметрия в литературе.
Примером зеркальной симметрии в литературе является всеми известный палиндром, или перевертень.
Палиндром-это фраза, читающаяся одинаково во всех направлениях
как слева направо, так и справа налево. Есть палиндромические имена собственные, как, например, Анна; существуют целые фразы-палиндромы. Классическим примером можно считать всем известную фразу А. Фета:
А роза упала на лапу Азора.
Но можно придумать и гораздо более длинные предложения:
Городничему в уме чин дорог.
Эти слова и фразы называют симметричными, хотя тут речь идет об особом виде симметрии. Это совершенно противоположно тому, что происходит с амбиграммами, где присутствует самая настоящая симметрия.
«Амбиграмма» происходит от англосаксонского термина, придуманного Дугласом Хофштадтером, профессором когнитивной психологии Университета Индианы. Слово АМА, например, считается амбиграммой, так как имеет осевую симметрию относительно вертикальной оси, делящей букву М на две равные части, что позволяет прочитать слово, поместив его половину рядом с зеркалом.
Слово OSO, наоборот, — пример центральной симметрии: оно прочитается, даже если слово повернуть на 180°. Слово СОСО — уже другой тип амбиграммы. Здесь мы видим центральную симметрию относительно горизонтальной оси: слово одинаково читается и в перевернутом виде, и у зеркала.
Четыре меня.
Моя зима из мёда и из мяты,
Приходит, как всегда, - вдвоём - с ангиной,
Истериками сны мои измяты,
А стены изрисованы сангиной.
Моя весна из молока и мела -
Бледна, как я. Мой голод невменяем:
И сколько бы любви я не имела, -
Я ем её, но будто не в меня ем.
Мне лето не дает страдать и злиться.
Мне лето - как близнец. Идем с ним в сквер, но
Ему не успеваю я излиться -
В затылок осень стужей дышит скверно.
Автор Челмакина Наталья – выпускница школы
.
Человек-существо симметричное.
Многие художники обращали пристальное внимание на симметрию и пропорции человеческого тела, во всяком случае до тех пор, пока ими руководило желание в своих произведениях как можно точнее следовать природе. Известны каноны пропорций, составленные Альбрехтом Дюрером и Леонардо да Винчи. Согласно этим канонам, человеческое тело не только симметрично, но и пропорционально. Леонардо открыл, что тело вписывается в круг и в квадрат. Дюрер занимался поисками единой меры, которая находилась бы в определенном соотношении с длиной туловища или ноги (такой мерой он считал длину руки до локтя).
Не станем пока разбираться, существует ли на самом деле абсолютно симметричный человек. У каждого, разумеется, обнаружится родинка, прядь волос или какая-нибудь другая деталь, нарушающая внешнюю симметрию. Левый глаз никогда не бывает в точности таким, как правый, да и уголки рта находятся на разной высоте, во всяком случае у большинства людей.
И все же это лишь мелкие несоответствия. Никто не усомнится, что внешне человек построен симметрично: левой руке всегда соответствует правая.
Полная безукоризненная симметрия выглядела бы нестерпимо скучно. Именно небольшие отклонения от нее и придают характерные, индивидуальные черты.
И в одежде человек тоже, как правило, старается поддерживать впечатление симметричности: правый рукав соответствует левому, правая штанина — левой.
Пуговицы на куртке и на рубашке сидят ровно посередине, а если и отступают от нее, то на симметричные расстояния.
Но на фоне этой общей симметрии в мелких деталях мы умышленно допускаем асимметрию, например расчесывая волосы на косой пробор — слева или справа.. Или надев кольцо на безымянный палец только одной руки.
Полная безукоризненная симметрия выглядела бы нестерпимо скучно. Именно небольшие отклонения от нее и придают характерные, индивидуальные черты.
Ассиметрия
Я хочу сказать, что в мире не все так симметрично, поэтому ученые ввели понятие ассиметрия.
Ассиметрия- отсутствие или нарушение симметрии. Чаще всего термин употребляется в отношении визуальных объектов и в изобразительном искусстве
Симметрия на шахматной доске
Рассмотрим шахматную доску. Итак, мы видим, что на шахматной доске есть координаты, также на ней есть и симметрия, геометрия тоже не обошла её стороной. Если каждую точку данной фигуры сместить каким-нибудь образом, то мы получим новую фигуру. Говорят, что эта фигура получена преобразованием из данной.
Симметрия.
Очень простой, но мощный и красивый метод решения игровых задач - симметричная стратегия. Суть его - делать каждый раз ход, симметричный ходу противника или дополняющий его до чего-либо. Доказательство правильности нашей стратегии будет пользоваться тем, что после каждого нашего хода позиция симметрична: раз так, то если противник сумел сделать свой ход, то и мы сможем сделать ход, симметричный ему.
Рассмотрим задачу.
Двое по очереди кладут пятаки на круглый стол так, чтобы они не накладывались друг на друга и не выступали за край стола. Проигрывает тот, кто не может сделать ход. Кто выиграет?
Решение. Нам нужно найти такую последовательность ходов, которая позволила бы, глядя на ходы соперника, делать ходы, которые привели бы к победе. Как же ходить после хода соперника? Стол круглый, поэтому первый ход так и просится — положить пятак в центр доски. А дальше? А дальше — по симметрии, относительно центра стола! И понятно, что первый выиграет.
Можно отметить, что если доска обладает центром симметрии (и не обязательно круглая), тогда первый сможет выиграть на ней действуя аналогичным образом: ставя свою фишку или монету в центр стола, а затем используя центральную симметрию.
Заметим, что симметрия бывает не только центральной, но и осевой. Рассмотрим одну из таких задач.
Двое по очереди ставят слонов в клетки шахматной доски 8x8 так, чтобы слоны не били друг друга. Проигрывает тот, кто не может сделать ход. Кто выиграет?
Решение. Здесь нет центральной клетки. А если бы и была, поставить симметрично относительно нее слона мы не можем, так как тогда слон вставал на поле, которое бьется слоном, который поставил соперник.
Но шахматная доска обладает другим свойством симметрии. У нее целых четыре оси симметрии. Используем симметрию относительно оси, которая проходит параллельно одной из сторон доски. Тогда, ставя своего слона симметрично относительно этой оси слону, поставленному первым игроком, выигрывает второй игрок.
Рассмотрим следующую задачу.
Имеется две кучки камней — по 7 в каждой. За ход можно взять любое количество камней, но только из одной кучки. Проигрывает тот, кто не может сделать ход. Кто выиграет?
Решение. Сначала опять используем метод малых задач.
Начнем игру с двух кучек, в каждой из которых по одному камню. Тогда, понятно, что первый проигрывает.
Если мы добавим в одну из кучек еще один камень, тогда понятно, что победит начинающий: он первым своим ходом возьмет из кучки, где два камня, один камень и получит позицию, которая получилась в рассмотренном выше случае, только сейчас он уже второй.
Если в кучках 3 и 1 камень, тогда вновь побеждает игрок, начинающий игру: он уравнивает число камней в кучках, т. е. берет два камня и получает, что число камней в кучках будет 1 и 1. И эта позиция, как уже рассматривалось выше, выигрышная для него.
Если число камней в кучках по 2, тогда вновь проигрывает начинающий: на любой его ход, противника может взять такое же число камней из другой кучки, которую первый игрок не тронул.
Сейчас несложно понять, как действовать игроку, делающему второй ход, чтобы победить в данной игре: он должен делать точно такие же ходы, как и первый, но только убирать камни он должен из той кучки, которую не тронул последним ходом его противник.
Как несложно понять, у победителя всегда есть ход после хода противника.
Несложно понять и общую стратегию выигрывающего, когда в кучках произвольное число камней:
если число камней в кучках равное, то необходимо уравнивать число камней в кучках после хода начинающего, выполняя симметричные ходы. Выигрывает второй игрок.
если же число камней в кучках неравное, тогда начинающий своим ходом уравнивает число камней в кучках и далее действует так же как, как и в первом случае. Здесь побеждает игрок, делающий первый ход.
В данной игре симметрия несколько необычная — вроде бы и не симметрия вовсе, однако, равенство камней в кучках, и «одинаковые» ходы, проводимые игроками очень ее напоминают.
Двое по очереди разламывают шоколадку 5 х 10. За ход можно сделать прямолинейный разлом любого из кусков вдоль углубления. Выигрывает тот, кто первым отломит дольку 1x1. Кто выиграет при правильной игре с обеих сторон?
Решение. Здесь идея использования симметрии очевидна. Ломаем шоколадку пополам, а далее первый из играющих «повторяет» ход второго игрока на равном куске, который не тронул своим ходом его соперник.
Повторение это длится до тех пор, пока после хода второго игрока не получится полоска вида 1 х k. Тогда первый отламывает от него кусочек 1 х 1 и выигрывает.
Понятно, что у первого игрока есть ход.
На окружности расставлено 20 точек. За ход можно соединить любые две отрезком, не пересекающим отрезки, проведенные ранее. Проигрывает тот, кто не может сделать ход. Кто выиграет при правильной игре?
Решение. Понятно, что сначала можно расположить точки на окружности так, как нам будет удобнее. Когда же мы расположим точки в вершинах правильного 20-угольника, то идея использования в решении симметрии сразу становится понятной. И первый отрезок можно провести таким образом, чтобы он делил нашу окружность пополам. А далее начинающий игрок отвечает строго по симметрии, относительно проведенного диаметра.
Отметим, что при решении задачи использовался новый прием, который называется «метод удобных фигур», т. е. сначала мы искали решение на удобной позиции, когда точки были в вершинах правильного 20-угольника.
Выводы. Заключение.
1.Изучив и исследовав тему «Симметрия вокруг нас», я узнал, что симметрией обладают объекты и явления живой природы и неживой природы.
2. Помимо осевой, зеркальной и центральной видов симметрии, которые мы изучаем в школьном курсе существуют и другие виды симметрии, которые могут сочетаться друг с другом.
3) Проблему симметрия – асимметрия следует понимать глубже. Симметрия и асимметрия настолько взаимосвязаны, что должны рассматриваться как две стороны единого понятия. Чем удачнее решает архитектор, композитор, поэт соотношение между симметрией и асимметрией, тем удивительней становится его творение.
4) Проектная работа расширила мой кругозор и помогла взглянуть на окружающий мир глазами исследователя. Рассматривая архитектуру зданий, предметы украшения и быта, технические изобретения, мы видим в них присутствие центральной, поворотной, переносной, осевой и зеркальной видов симметрии, которые дают ощущение спокойной уверенности и эстетической привлекательности.
5) Я на практике увидел межпредметные связи между математикой и физикой, русским языком и литературой, музыкой. Симметрия безгранична. Её проявления можно изучать бесконечно, поэтому я продолжу работать над этой проблемой и дальше исследовать. Я ещё раз убедился в том, что симметрия-это способ создания красоты. Таким образом, изучая симметрию законов природы, рано или поздно удается глубже проникнуть в сущность живого, объяснить ход эволюции и дать возможность человеку чаще применять данные законы симметрии в жизни.
Прекрасный, безграничный,
Наглядный и привычный,
Но всё же необычный,
Чудесный «симметричный»
Открылся мир вокруг. Я желаю вам успеха в его познании.
Литература:
1.Аммосова Н.В.; Коваленко В.В. Симметрии : теоретический и методический аспекты – Астрахань, 2012.
2.Вейль Г. Симметрия. Пер. с англ. - М.: Наука, 1968.
3.Гарднер М. Этот правый, левый мир. Пер. с англ. - М.: Просвещение, 1992.
4.Гильде В. Зеркальный мир. — М.: Мир, 1982.
5. Современный словарь иностранных слов. — М.: Русский язык, 1993.
6. Советский энциклопедический словарь — М.: Советская энциклопедия, 1980
7.Справочник школьника (раздел “математика”) М.Б.Волович – Москва “АСТ-ПРЕСС” 1999 года
8.Тарасов Л.В. Этот удивительный симметричный мир. Пособие для учащихся. – М.: Просвещение, 1982.
9. Шафрановский И.И. Симметрия в природе. –Л.: Недра, 1985.
10.Интернет.
14
Получите свидетельство
Вход
Материал к уроку по математике "Симметрия" (0.75 MB)
0
1642
29
Нравится
0
