Выступление
на заседании КМО
учителей математики
(руководитель Зубарева Т.В.)
«Эстетическая составляющая
урока математики»
учителя математики
ООШ с.Каменка
Ксенофонтовой Т.Н.
Пугачев
2012
Содержание
Введение
Умение заинтересовать математикой
Симметрия
"Красивые" задачи –
ключ к пониманию изящества математики
Математика в литературе
Задачи в литературных произведениях
Исследование учащихся по материалам произведений
Музыка и математика.
Понятие функции в жизни.
Заключение.
Эстетическая составляющая урока математики
Перед общеобразовательной школой во весь рост встает задача совершенствования системы получения знаний учащимся. Одним из эффективных путей решения этой важной проблемы является эмоциональная окрашенность всего процесса познания. Учебный процесс в школе пока что страдает сухостью. В нем много рациональности, но мало эмоциональности. А «знания вне чувства, по словам В. Г. Белинского, лишь светят, а не греют, не способны перейти в действие». Еще более категорично о необходимости эмоционального воздействия на воспитанников говорит А.В. Луначарский: «Не волнуя, не затрагивая нервную систему, нельзя даже просто агитировать, нельзя, например, даже собирать толпу и пойти тушить пожар. Тем более нельзя без этого воспитывать. Поэтому эмоциональной окраской учебного материала, вызвав эмоциональные порывы, вызвав эмоциями видоизменения в сознании учеников, можно придать воспитательный характер любому процессу восприятия того или другого внешнего воздействия». Итак, процесс познания немыслим без участия эмоций, то есть умственное воспитание невозможно без эстетического.
Слово «эстетика» в переводе с греческого означает чувственно воспринимаемый, имеющий отношение к чувственному восприятию. В этимологии слова, таким образом, раскрывается то важное обстоятельство, что эстетическое воспитание имеет главным объектом воздействия эмоции, чувства людей. Проблема эстетического воспитания не менее актуальна, чем проблема развития мыслительной деятельности, т.к. «человек утверждается в предметном мире не только через посредство мышления, а и через посредство всех чувств».
Эстетическое воспитание – целенаправленное формирование эстетических вкусов и идеалов личности, развитие ее способности к эстетическому восприятию явлений действительности и произведений искусства, а также к самостоятельному творчеству. Эстетическое воспитание – это своеобразное, специфическое средство решения общей задачи воспитания человека.
Эмоции ведут к более экономному познанию мира. О возможности эстетического воспитания на всех уроках без исключения говорил еще в свое время К.Д. Ушинский: «…во всякой науке более или менее есть эстетический момент, передачу которого должен иметь наставник». Высокое назначение урока - практически показывать детям, подросткам и юношам красоту человеческой мысли, эстетику самого поиска истины. А между тем, урок в его нынешнем состоянии далеко не всегда ориентирует ребят на постоянные поиски изящных решений и доказательств, не раскрывает красоту мысли, не ведет учеников по пути овладения процессом экономного и в тоже время правильного мышления. Красота в
науке – пока необязательное для школы попутное явление. Порой в рассказах учителей господствуют стершиеся, обезличенные выражения, не доходящие до сознания ученика.
Серый, бесцветный, невыразительный язык не создает в школе атмосферы «музыкальности в области мысли». Часто ли слышат ребята об увлекательности познания? Увы, нет! Мы толкуем им о красоте природы, о человеческой красоте, о поэзии и искусстве. Но они не слышат от учителя слов: «поэзия науки», «радость познания».
«Науку противопоставляют отчасти красоте, но это несправедливо. Если бы наука своими результатами могла действовать так же открыто и легко, как произведение художества, то она и была бы художеством. Астрономия, ботаника, история, математика, если содержание их вполне соответствует форме, художественны в высшей степени; но, чтобы наслаждаться этими художествами, - нужно много приготовлений, много посредствующих мыслей, и чувство убивается; пусть результаты астрономии сделаются доступны одному взгляду человека, и это будет высокая поэма».
Конечно, эстетика научного познания в действительности - трудная задача. Скажем, «радость природы» или «радость искусства» - более легкая радость, чем «радость умственного труда». Последняя дается в борьбе, в усилиях. Но дело не только в этом. Сама по себе наука содержит лишь предпосылки для получения учеником радости, понимания ее своеобразной красоты, проявления творческих сил.
Чтобы эти предпосылки реализовались, необходимо соответствующим образом построить процесс обучения.
Но в науке к этой мысли, глубокой, как море, светлой и радостной, как солнце, мы доходим долгим путем рассудка, а здесь одним взглядом, одним порывом вызываемого чувства. Вот разница между наукой и художеством». По словам Перрона «еще прекраснее, чем готовая истина, сами поиски истины». Познание, поиск истины, эксперименты представляют собой непрерывное творческое горение, приносящее человеку наивысшее наслаждение.
По образному выражению Л.Н. Толстого «Наука и искусство так же тесно связаны между собой, как легкие и сердце, так что, если один орган извращен, то и другой не может правильно действовать».
Эстетическое воспитание, особенно на таких уроках, как математика, русский язык, химия, физика, - это пока еще легкая «педагогическая целина». Сегодня уже никто не сомневается в могуществе математических методов познания мира, но не все чувствуют связь математики с красотой. Мы с восхищением смотрим на очертания современных самолетов, на ажурное плетение радиобашни, обтекаемые формы кораблей на подводных крыльях, но ведь все это появилось сначала в виде совершенных математических формул. У математики особая красота. Красота высот математического мышления начинается со школьного урока математики. Трудно встретить такого ребенка, который не тянулся бы к школе с ожиданием чудесной новизны.
Эта новизна обязательно должна включать продолжение детских забав и игр и быть в то же время частью настоящей жизни взрослых. Именно это сочетание и создает в большей мере эстетические нормы обучения. Когда же обстановка работы исключает игру, фантазию, когда фон мрачный гаснет радость познания. Поэтому все то, что делается в классе, школе, необходимо рассматривать и оценивать не только с точки зрения педагогики, но и эстетики, причем все это должно быть не только разумным и добрым, но и прекрасным. Пусть ученик ко всему, что изучает, относится эстетически, и тогда эрудиция, образованность, знания никогда не станут союзниками безнравственности и равнодушия.
Высокое назначение учителя – умело руководить процессом постижения прекрасного, раскрывать перед воспитанниками сущность эстетических элементов в научном познании действительности, практически показывать детям красоту человеческой мысли, эстетику самого поиска истины.
А между тем, влияние искусства на развитие эмоциональной сферы школьника, личностные качества, развитие фантазии, интуиции, воображения – доказывают и научные исследования и повседневная жизнь. Эмоционально развитый ребенок во много раз быстрее освоит науки, справится с любыми проблемами успешнее, чем человек – робот, многому обученный, но мало чувствующий. Искусство активизирует взаимодействие левого и правого полушария настолько, что снижается ассиметрия, возрастает творческий потенциал, повышается познавательная активность. Очень важно, чтобы способы познания мира научный и художественный гармонично сочетались в урочной и внеурочной деятельности. Только единство этих двух видов познания, их гармония могут дать нам мыслящую, чувствующую личность, способную к преобразованию жизни по законам красоты.
Математика с самого начала была связана с искусством. Долгое время затруднялись, куда ее отнести к естественным или гуманитарным наукам. Первые теоретические образы прекрасного и первые абстракции, понятия о прекрасном были связаны с математикой и созданы на основе математики.
Математика - это язык, на котором говорят не только наука и техника, математика – это язык человеческой цивилизации. Она практически проникла во все сферы человеческой жизни. Современное производство, компьютеризация общества, внедрение современных информационных технологий требует математической грамотности. Это предполагает и конкретные математические знания, и определенный стиль мышления, вырабатываемый математикой.
СОВЕРШЕНСТВО ЯЗЫКА – ещё один признак красоты математики. Математический язык – это по преимуществу язык символов и формул, чрезвычайно точный, ясный и вместе с тем предельно краткий; язык, который не утомляя нашего внимания, одной чертой выражает обширные понятия.
Любой урок математики – это урок по развитию речи учащихся, он должен быть направлен на совершенствование точности и последовательности выражения мыслей каждого участника образовательного процесса.
Основная задача школьного образования сегодня заключается в том, чтобы превратить процесс постижения эстетической стороны математики из процесса стихийного в осознанный, научно управляемый. Учитель должен быть находчив в показе красивого. Эмоциональная подача материала педагогом, эмоциональный урок в целом вызывают ответные эмоции учащихся, содействуют активизации умственной деятельности и успешному усвоению учебного материала. Наука математика!
Сколько романтики и красоты заключено в колонках абстрактных чисел и понятий! Хорошо бы раздвинуть контакты с математикой вширь и вглубь!
Красота – есть нечто общедоступное. Каждый человек знаком с нею по своему собственному чувственному опыту. Даже маленькие дети уверенно чувствуют различия между предметами красивыми и некрасивыми. Осмысливание красоты, выражение её в понятии произошло довольно рано в истории человечества и происходит в начальный период развития понятийного мышления каждого человека.
Уроки математики в этом смысле - великолепная возможность для решения задач умственного и эстетического воспитания учащихся.
Красоту математики (её простоту, симметрию, сжатость и полноту) можно и следует дать почувствовать даже очень малым детям. Когда этот предмет излагают должным образом и притом конкретно, то усвоение математики сопровождается эмоциями и наслаждением красотой.
Юнг
Одна из воспитательных задач учителя математики заключается в формировании эстетического вкуса школьников с помощью использования эстетического потенциала уроков математики, который призван повысить интерес обучающихся к предмету и формировать ценностный потенциал воспитанников, то есть их эмоциональную сферу и творческие способности через восприятие математики как тонкой изящной науки.
Потребность, которая вызвала необходимость обратиться к данному вопросу, обусловлена различным восприятием математики обучающимися и учителем.
Математика



(глазами обучающихся)

точная сложная скучная
при изучении нет места творчеству, изяществу, красоте
прагматическое отношение
(выучить, чтобы сдать экзамены, поступить в ВУЗ и т.д.)
обучающиеся не чувствуют внутрипредметную красоту математики,
силу её эмоционального воздействия
происходит притупление интереса к математике
как к изучаемому предмету и как к науке вообще
Математика




(глазами учителя)
точная интересная полезная красивая

изящная увлекательная
математика – главное звено,
направленное на интеллектуальное развитие обучающихся,
на воспитание нравственно-эстетических ценностей каждого человека,
на формирование логического и аналитического мышления,
пространственного воображения
математику нужно представлять не как систему истин,
которые надо заучивать,
а как систему рассуждений, требующих творческого мышления,
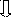
что в свою очередь приводит к развитию личности
необходимо заинтересовать предметом
через видение внутренней красоты математики,
через занимательность и привлекательность задач,
сделать математику более доступной
Успешность процесса изучения математики зависит, прежде всего, от желания обучающихся овладеть основами науки, а это возможно лишь при заинтересованности предметом. Важнейшим фактором успеха в обучении является интерес к предмету, следовательно, и учебник, и урок должны быть увлекательными. Обучение должно вызывать удовольствие. Математику можно представить в виде рассуждений, требующих творческого мышления. В процессе такого обучения появляется интерес, то есть желание учиться, а "где есть желание, найдется путь" (Д. Пойа).
Умение заинтересовать математикой – дело непростое, и в этом смысле личного мастерства учителя нельзя недооценивать. Многое зависит от того, как поставить даже очевидный вопрос, и от того, как вовлечь всех обучающихся в обсуждение сложившейся ситуации. Перед учителем математики стоит ряд задач: как привить вкус, интерес, видение красоты в математических задачах, как развивать творческую деятельность обучающихся. Творческая активность учеников, успех урока целиком зависят от методических приемов, которые выбирает учитель.
Эстетической привлекательностью математических объектов занимались многие ученые, исследуя красоту математики. В.Г. Болтянский, Г. Биркгоф и другие выводили формулы "математической эстетики". В них красота математического объекта обусловлена взаимодействием его обобщенного образа, созданного нашей психикой, и оригинальности, выделяющей этот объект из множества других.
Что можно рассматривать на уроках математики, предвещающих красоту, стройность, закономерность? И как это связать с искусством и живописью?
Симметрия является той идеей, посредством которой человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство. (Г.Вейгель)
Т.О., симметрия воспринимается человеком как проявление закономерности, порядка, царящего в природе. Итак, целесообразность симметрических форм была осознана человечеством в доисторические времена, а в сознании древних греков симметрия стала олицетворением закономерности, целесообразности, а следовательно и красоты.
Симметрия
(Презентация)
Важной мерой красоты является порядок, который выступает в различных формах. Наиболее распространенной из них является симметрия. Поэтому развитие интереса к предмету математики, а так же творчества обучающихся можно реализовать в процессе изучения темы "Симметрия".
"Красивые" задачи –
ключ к пониманию изящества математики
О красоте математики написано немало. Многие авторы видят её в гармонии чисел и форм, геометрической выразительности, стройности математических формул, решении задач различными способами, изяществе математических доказательств, порядке, универсальности математических методов. Под понятие красоты подводится широкий спектр различных объектов, начиная от схем зверушек, составленных из отрезков, до представления красивой модели, удовлетворяющей требованиям простоты, неожиданности, изоморфизма.
Ученые, исследуя красоту математики, давали различные формулы эстетической привлекательности математического объекта. Например, Г. Биркгоф дал следующую формулу: 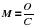 , где М – мера красоты объекта, О – мера порядка, С – мера усилий, затрачиваемых для понимания сущности объекта. А у В.Г. Болтянского своя формула "математической эстетики":
, где М – мера красоты объекта, О – мера порядка, С – мера усилий, затрачиваемых для понимания сущности объекта. А у В.Г. Болтянского своя формула "математической эстетики":
красота = наглядность + неожиданность + простота + …
И та, и другая формулы созвучны: в них красота математического объекта обусловлена взаимодействием его обобщенного образа, созданного нашей психикой, и оригинальности, выделяющей этот объект из множества других.
В качестве источников эстетической привлекательности математических объектов (понятий, теорем, задач, доказательств и т.д.) выступают категория порядка, проявляющаяся в гармонии отдельных частей, их симметрии, в логической стройности, и категория простоты, раскрывающаяся в неожиданности, обусловленной контрастом между трудностью проблемы и простотой методов, используемых для её решения.
Эффективное раскрытие эстетического потенциала математики возможно лишь в процессе творческой деятельности обучающихся. А в этой деятельности ведущая роль принадлежит задаче, "красивой" задаче, её изящному решению.
Красивое решение должно нас чем-то удивить, должно быть в чем-то неожиданным. Если мы хотим понять некоторое явление, яснее его представить, то мы прибегаем к наглядной модели изучаемого явления. Наглядная модель должна правильно отражать те основные черты явления, которые следует изучить.
Основным требованием к модели является её простота для восприятия, для оперирования с нею. Благодаря простоте модели, можно легче сделать необходимые выводы. При решении любой непростой задачи обучающиеся составляют для себя наглядную модель описываемого в задаче явления. В этот момент и происходит проявление творческого подхода к решению задачи. Удачный выбор наглядной модели нередко предопределяет успех дела, а необычность этой модели, её неожиданность воспринимаются как красота и изящество решения.
Каждая математическая задача служит конкретным целям обучения, но основная её роль – развитие творческого и математического мышления обучающихся, повышение их интереса к математике. Для того, чтобы обучающиеся осознали эстетику задачи, необходимо знакомить их с различными способами её решения, различными приемами доказательства одной и той же теоремы. Восприятие эстетической стороны задачи начинается с условия и чертежа. Поэтому содержание условия должно вызывать интерес, чертеж должен соответствовать значению слова "красивый", то есть доставляющий наслаждение, приятный внешним видом, гармоничностью, стройностью.
Итак, математическая задача способствует формированию и развитию эстетического вкуса учеников в том случае, если она отвечает определенным требованиям, а именно:
условие задачи должно быть интересно школьнику, если задача геометрическая, то чертеж должен быть "красивым";
задача может устанавливать интересный факт, порой неожиданный;
задача должна обладать большой степенью общности;
в решение задачи обязательно нужно спрятать "изюминку", чтобы оно было наглядно и удивительно просто;
желательно, чтобы было несколько способов решения задачи.
Формируя и развивая эстетический вкус обучающихся при решении "красивых" задач, учитель помогает школьникам более полно воспринять красоту математики вообще, старается повысить их математическую и общую культуру.
Математика в литературе
(Презентация)
Что любят, то находят повсюду, и было бы странно не встретиться с математикой в художественной литературе. Почему странно? Потому что, как верно заметил А.Блок, сама истинная поэзия, сами настоящие стихи – это «математика слова». Ничем иным является, в сущности, и настоящая проза. Так что, видимо, всякий действительный художник – немножко математик.
Потому что в жизни нет ничего такого, чего бы не было в романах, рассказах и стихах, а математика – слишком заметная тема жизни, чтобы не стать темой литературы. И не только сама она, её значение, отношение к ней, но и многое-многое другое связанное с математикой. Кажется, без математических фрагментов не получилось бы ни «Скифов» Блока, ни «Автобиографии» Нушича, ни «Персидских писем» Монтескье, ни сотен других прекрасных вещей.
Читая художественную литературу и неожиданно встречая математическое место у Пушкина или Толстого, воспринимаешь его с особым интересом уже потому, что здесь не требуется ни заучивать, ни решать, а всего лишь понять и почувствовать красоту мысли и слова великого художника. И покорённый этой красотой, смотришь на математику глазами автора и проникаешься его отношением к ней.
Я считаю, что интересно знакомиться с теми произведениями, авторы которых отзываются о математике положительно, потому что красота лирических слов помогает изменить мнение о том, что математика и литература несовместимы.
Тема математики в литературе интересна и неповторима.
Музыка и математика.
(Презентация)
Сегодня эти два слова редко стоят вместе. Между тем именно в музыке впервые была обнаружена таинственная направляющая роль чисел в природе.
Истоком разработки урока явились слова великого композитора Игоря Стравинского «Музыка математична». Поэтому, целью урока стало выявление родственности смыслов понятия функции в музыке и математике.
Выдержка из урока: «Функция. Какого цвета и как звучит таблица умножения?»
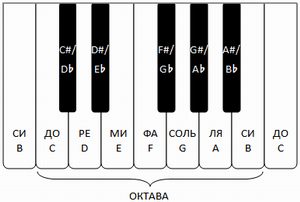
Сегодня на уроке мы с вами рассмотрим более широкое представление понятия «функция» и выявим интересную зависимость между натуральными числами, цветами радуги и нотами в музыкальной гамме. Ребята, сколько всего нот в музыкальной гамме? Кто перечислит их? Сколько цветов радуги?
Эти семь нот лежат в основе любой музыки. Самая разная и при разных обстоятельствах звучит в нашей жизни музыка. Она звучит по радио, телевидению, в кино, в грамзаписи; музыка заполняет концертные и театральные залы; мы слышим музыку в детских садах и школах, на спортивных соревнованиях, в цирке и на дискотеке.
Музыка, также как и литература, и живопись, и математика расширяет наше знакомство с окружающим миром.
Оказывается, можно установить зависимость между множеством всех натуральных чисел, цветами радуги и нотами.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| к | о | ж | з | г | с | ф |
1
2
Числу 1 соответствует нота «до», числу 2 – «ре» и далее по таблице. Начиная с числа 8, все повторяется. А как определить ноту для числа 29? Правильно, надо найти остаток от деления 29 на 7! Это будет 1. Значит, числу 29 соответствует нота «до». А как определить ноту для числа 35? Верно, число 35 делится нацело на 7, значит, ему соответствует нота «си».
В начальных классах мы с вами учили таблицу умножения (оказывается, она является трудом древнегреческого ученого Пифагора – в этом учебном году вам предстоит доказать его знаменитую теорему). Интересно то, что таблицу можно сыграть на музыкальном инструменте, но для этого ее надо переложить на ноты.(Презентация)
Пример работы учащихся. Функции в жизни.
В своей работе я привела лишь некоторые примеры, подтверждающие многие теоретические положения об эстетическом потенциале уроков математики. Сопровождая свои уроки различными методами и способами подачи математического материала, я стараюсь повышать его привлекательность. В результате такого обучения ученики начинают смотреть на задачи как на исследовательские объекты, в которых скрыта гармония и красота математики, наслаждаясь тем, что в процессе работы эти качества математики обнажаются, и красота математики становится для ребят доступной.
Эстетическая сторона математики раскрывается в использовании школьниками обобщения и аналогии, наглядности и выразительности математических объектов, всестороннего анализа изучаемых ситуаций, поиска и выбора наиболее изящного способа решения, логической обоснованности и доказательности.
Искренне считаю, что жизнь настоятельно требует сегодня сделать эстетику не гостьей на уроке, а эффективным средством превращения ученика в чувственного, гуманного, творческого человека.

 Получите свидетельство
Получите свидетельство Вход
Вход







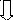
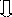
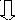
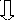




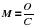 , где М – мера красоты объекта, О – мера порядка, С – мера усилий, затрачиваемых для понимания сущности объекта. А у В.Г. Болтянского своя формула "математической эстетики":
, где М – мера красоты объекта, О – мера порядка, С – мера усилий, затрачиваемых для понимания сущности объекта. А у В.Г. Болтянского своя формула "математической эстетики": 









 Доклад на МО учителей математики "Эстетическая составляющая урока математики" (66.06 КB)
Доклад на МО учителей математики "Эстетическая составляющая урока математики" (66.06 КB)
 0
0 2862
2862 396
396 Нравится
1
Нравится
1


