Шар. Сфера

Презентация по геометрии по теме "Шар. Сфера" включает в себя 30 слайдов к темам уроков: Сфера и шар, Применение сферы, Сечения шара плоскостью. Касательная плоскость, Площадь поверхности сферы. Объем шара, Решение задач.

«Сфера и шар»

http://lapinagv.jimdo.com/

• Сфера и шар, так же как окружность и круг, рассматривали еще в глубокой древности .
• Открытие шарообразности Земли, появление представлений о небесной сфере дали толчок к развитию специальной науки – СФЕРИКИ , изучающей расположенные на сфере фигуры.
• Автором первого сочинения о «сферике» был математик и астроном Евдокс Книдский (ок.408 – 355 до н.э.).

http://lapinagv.jimdo.com/

• Шаром называется тело, которое состоит из всех точек пространства, находящихся на расстоянии, не большем данного ( радиус шара ), от данной точки ( центр шара ).

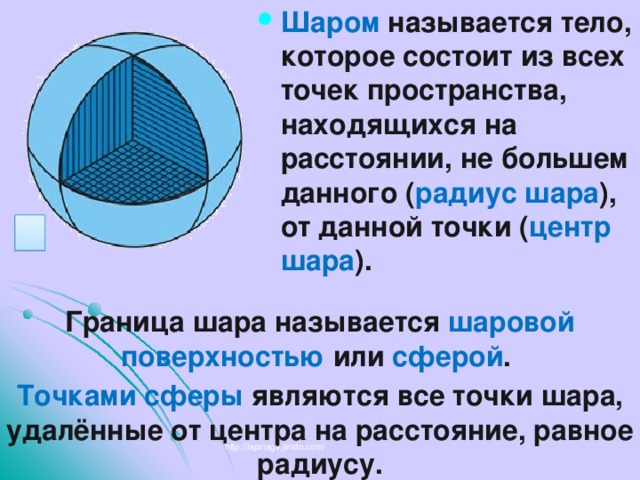
Граница шара называется шаровой поверхностью или сферой .

Точками сферы являются все точки шара, удалённые от центра на расстояние, равное радиусу.

http://lapinagv.jimdo.com/

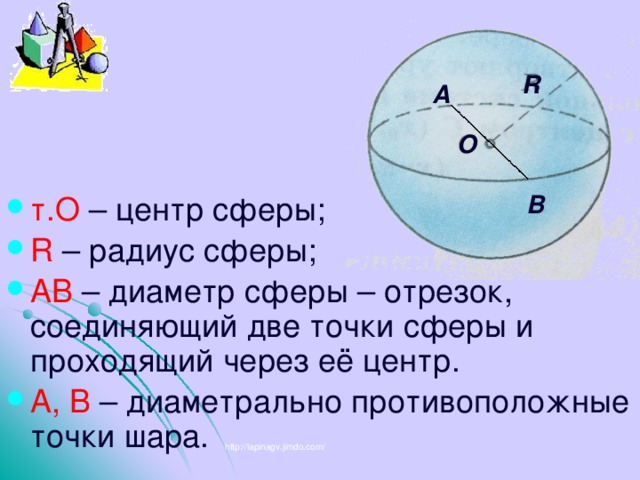
R

А

О

В

• т.О – центр сферы;
• R – радиус сферы;
• АВ – диаметр сферы – отрезок, соединяющий две точки сферы и проходящий через её центр.
• А, В – диаметрально противоположные точки шара.

http://lapinagv.jimdo.com/

Шар – тело вращения полукруга вокруг его диаметра как оси

http://lapinagv.jimdo.com/

Сфера – тело вращения полуокружности вокруг его диаметра как оси

http://lapinagv.jimdo.com/

Применение сферы

http://lapinagv.jimdo.com/

• Сферическая геометрия нужна не только астрономам , штурманам морских кораблей, самолетов, космических кораблей, которые по звездам определяют свои координаты, но и строителям шахт , метрополитенов , тоннелей , а также при геодезических съёмках больших территорий поверхности Земли, когда становится необходимым учитывать её шарообразность.

http://lapinagv.jimdo.com/

Сечения шара плоскостью.

Касательная плоскость.

http://lapinagv.jimdo.com/

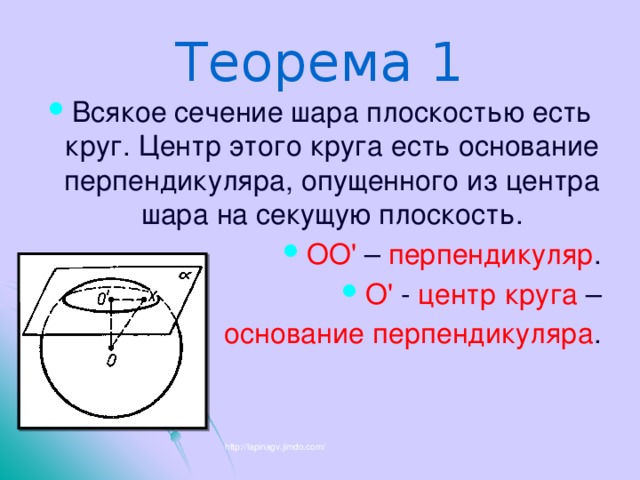
Теорема 1

• Всякое сечение шара плоскостью есть круг. Центр этого круга есть основание перпендикуляра, опущенного из центра шара на секущую плоскость.
• ОО' – перпендикуляр .
• О' - центр круга –

основание перпендикуляра .

http://lapinagv.jimdo.com/

Сечение шара

• Плоскость, проходящая через центр шара, называется диаметральной плоскостью .

• Сечение шара диаметральной плоскостью называется большим кругом , а сечение сферы - большой окружностью .

http://lapinagv.jimdo.com/

Теорема 2

• Любая диаметральная плоскость шара является его плоскостью симметрии. Центр шара является его центром симметрии.

http://lapinagv.jimdo.com/

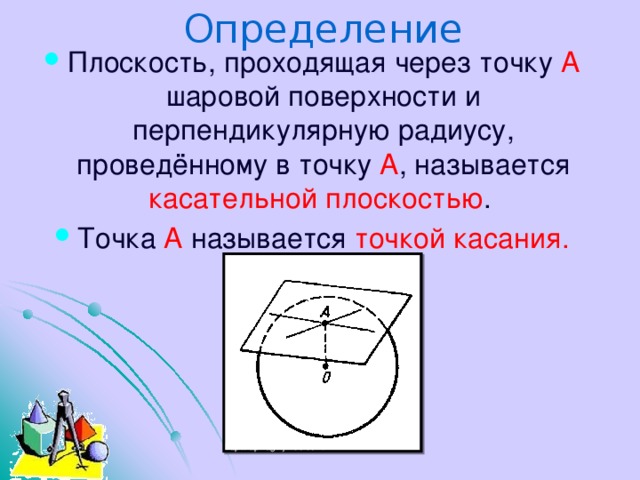
Определение

• Плоскость, проходящая через точку А шаровой поверхности и перпендикулярную радиусу, проведённому в точку А , называется касательной плоскостью .
• Точка А называется точкой касания.

http://lapinagv.jimdo.com/

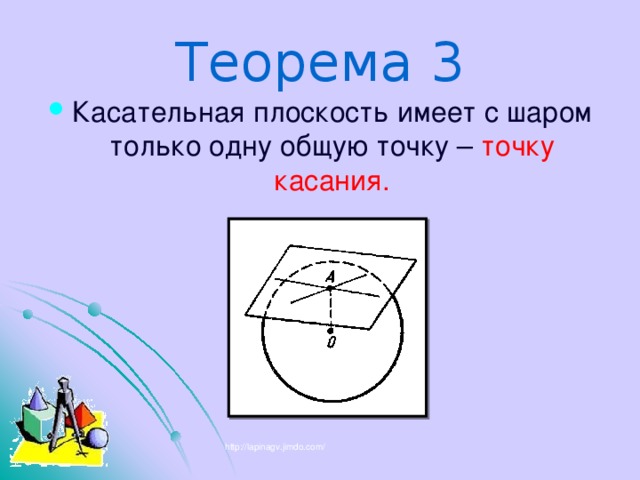
Теорема 3

• Касательная плоскость имеет с шаром только одну общую точку – точку касания.

http://lapinagv.jimdo.com/

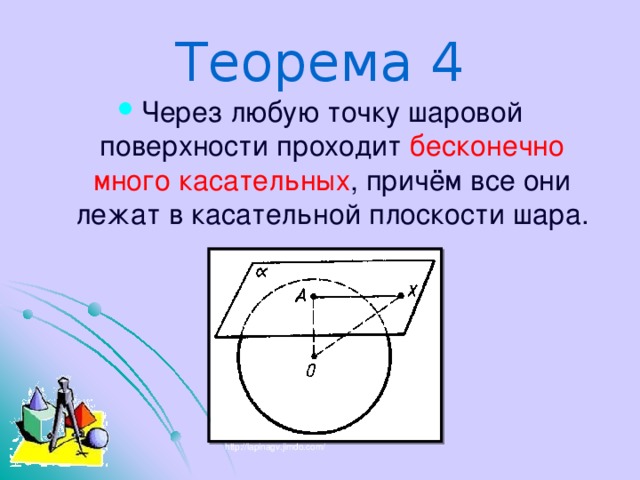
Теорема 4

• Через любую точку шаровой поверхности проходит бесконечно много касательных , причём все они лежат в касательной плоскости шара.

http://lapinagv.jimdo.com/

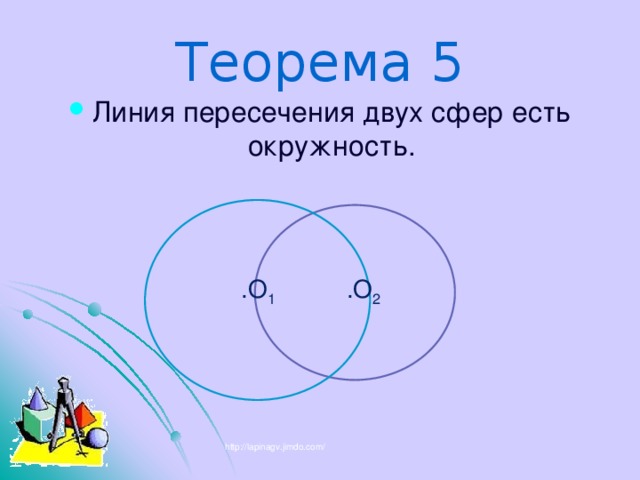
Теорема 5

• Линия пересечения двух сфер есть окружность.

.О 1

.О 2

http://lapinagv.jimdo.com/

Задача

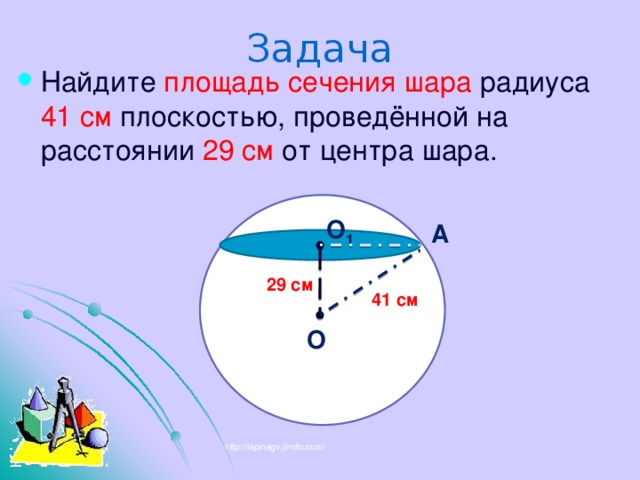
• Найдите площадь сечения шара радиуса 41 см плоскостью, проведённой на расстоянии 29 см от центра шара.

О 1

А

29 см

41 см

О

http://lapinagv.jimdo.com/

Площадь поверхности сферы,

объём шара.

http://lapinagv.jimdo.com/

Уравнение сферы

• Пусть центр сферы в т. А(a, b, c), радиус сферы – R.
• Квадрат расстояния от т. (x, y, z) до т. А:
• (x-a) 2 + (y-b) 2 + (z-c) 2 =R 2

• Уравнение сферы с центром в начало координат:
• x 2 + y 2 + z 2 =R 2

http://lapinagv.jimdo.com/

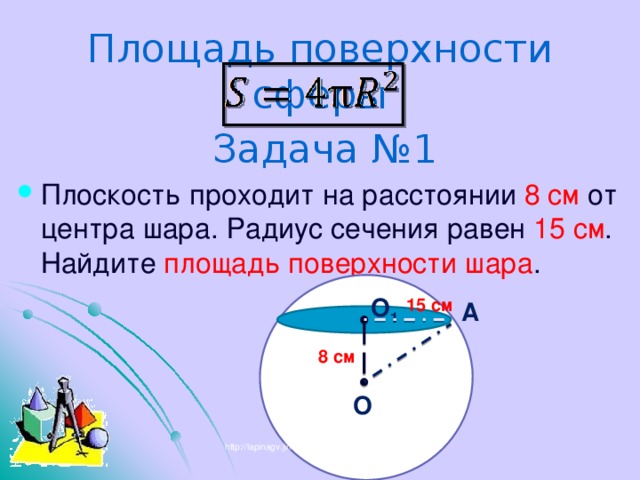
Площадь поверхности сферы

Задача №1

• Плоскость проходит на расстоянии 8 см от центра шара. Радиус сечения равен 15 см . Найдите площадь поверхности шара .

О 1

15 см

А

8 см

О

http://lapinagv.jimdo.com/

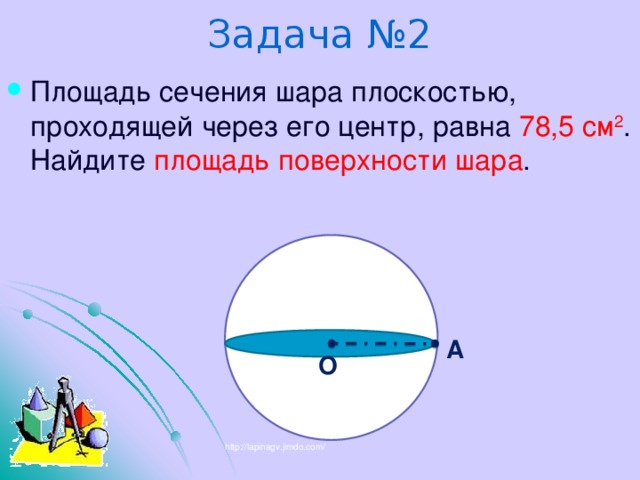
Задача №2

• Площадь сечения шара плоскостью, проходящей через его центр, равна 78,5 см 2 . Найдите площадь поверхности шара .

А

О

http://lapinagv.jimdo.com/

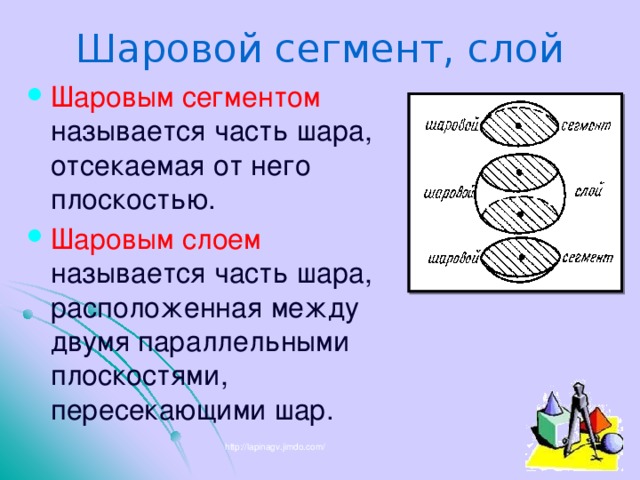
Шаровой сегмент, слой

• Шаровым сегментом называется часть шара, отсекаемая от него плоскостью.
• Шаровым слоем называется часть шара, расположенная между двумя параллельными плоскостями, пересекающими шар.

http://lapinagv.jimdo.com/

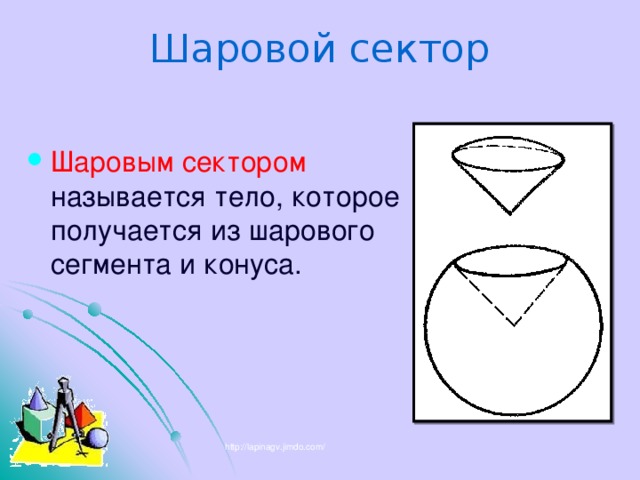
Шаровой сектор

• Шаровым сектором называется тело, которое получается из шарового сегмента и конуса.

http://lapinagv.jimdo.com/

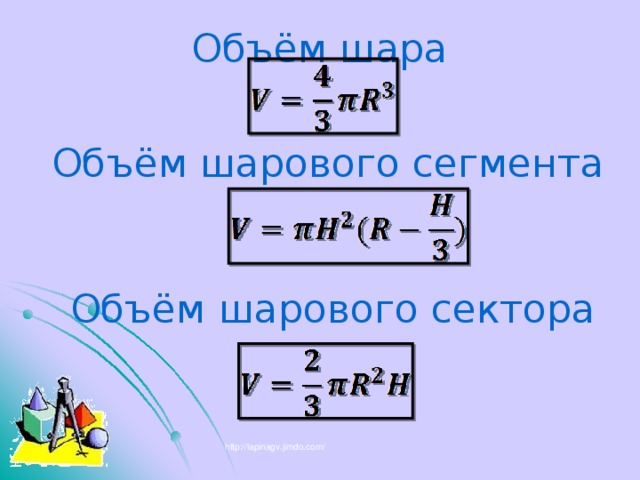
Объём шара

Объём шарового сегмента

Объём шарового сектора

http://lapinagv.jimdo.com/

Объем шара и площадь сферы.

• Архимед интерпретировал эти формулы так:
• объем и поверхность шара составляют 2/3 от объёма и полной поверхности описанного около шара цилиндра .

http://lapinagv.jimdo.com/

Решение задач

http://lapinagv.jimdo.com/

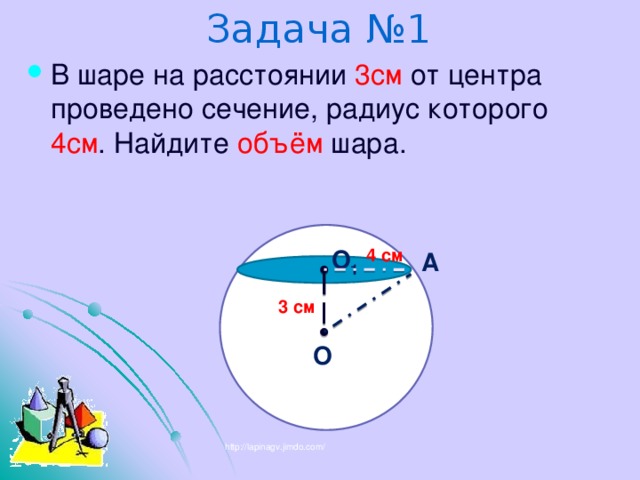
Задача №1

• В шаре на расстоянии 3см от центра проведено сечение, радиус которого 4см . Найдите объём шара.

4 см

О 1

А

3 см

О

http://lapinagv.jimdo.com/

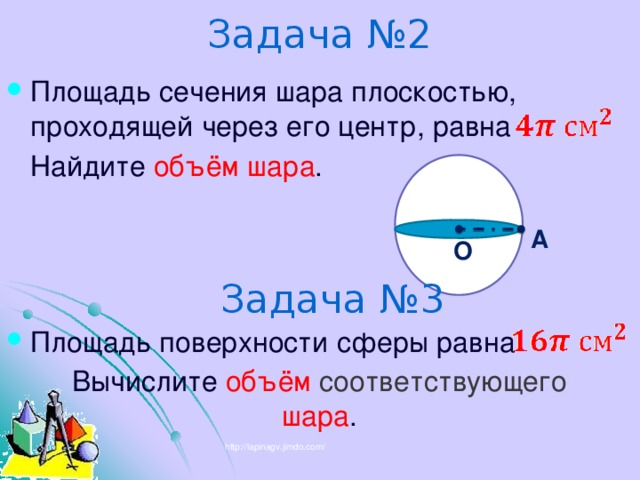
Задача №2

• Площадь сечения шара плоскостью, проходящей через его центр, равна

Найдите объём шара .

А

О

Задача №3

• Площадь поверхности сферы равна

Вычислите объём соответствующего шара .

http://lapinagv.jimdo.com/

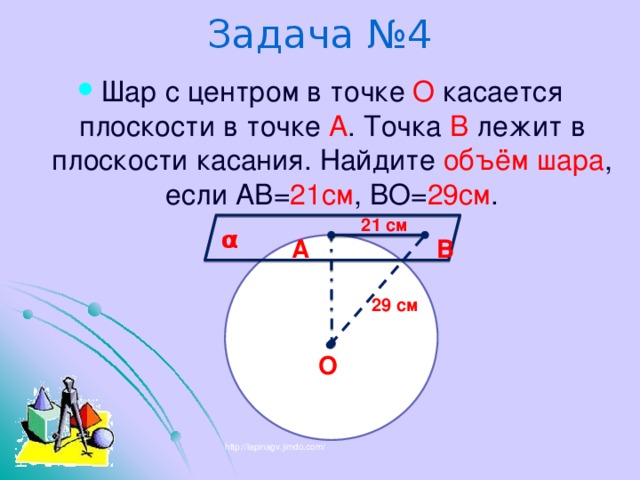
Задача №4

• Шар с центром в точке О касается плоскости в точке А . Точка В лежит в плоскости касания. Найдите объём шара , если АВ= 21см , ВО= 29см .

21 см

α

В

А

29 см

О

http://lapinagv.jimdo.com/

Задача №5

• Объём шара равен . Найдите площадь поверхности шара .

Задача №6

• Сумма площадей поверхностей двух шаров радиуса 4 см равна площади поверхности некоторого большего шара. Каков объём этого большего шара?

http://lapinagv.jimdo.com/