Получите свидетельство
Вход
Сандық функция. Функцияның берілу тәсілдері, функциялардың графигтерін қарапайым түрлендіру.
y=ax+b сызықтық функцияның графигі – түзу,
- y=ax2+bx+c квадраттық функцияның графигі – парабола,
- y=k/x кері тәуелділіктің графигі – гипербола екені көрсетіліп, фигураларды түрлендіру түрлері қарастырылды. Енді осылардың негізінде y=kf(ax+b)+d (мұндағы k, a,b, d – нөлден өзгеше сандар) функциясының графигін қарапайым түрлендірулер қолдану арқылы салу жолын қарастырайық.
облысында анықталған y=f(x) функциясының графигі қисық сызық болcын. Бұл графикке төмендегідей түрлендірулер қолдануға болады.
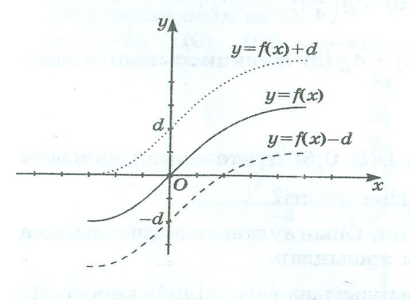
І. y=f(x)+d функциясының графигі y=f(x) функциясының графигін Оу ордината осінің бойымен, егер d0 болса, онда d бірлікке жоғары, ал d
1-мысал, а)
ә)
функцияларының графигін салайық.
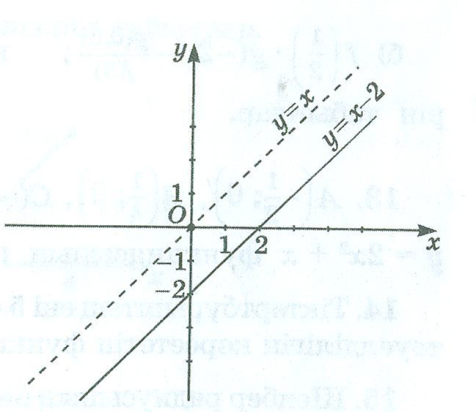
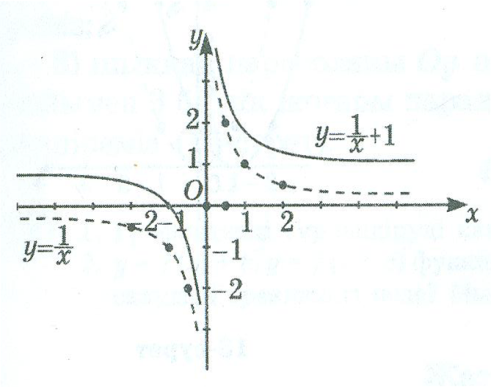
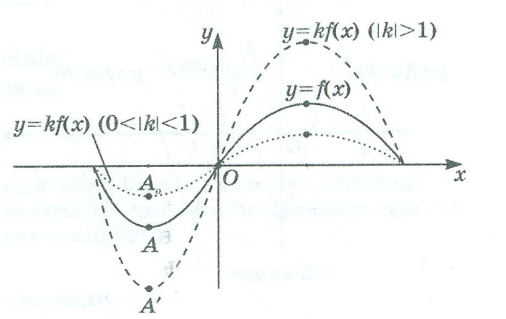
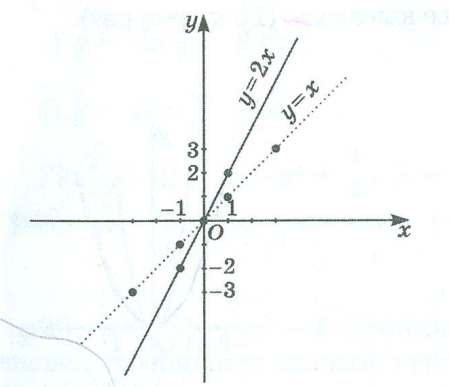
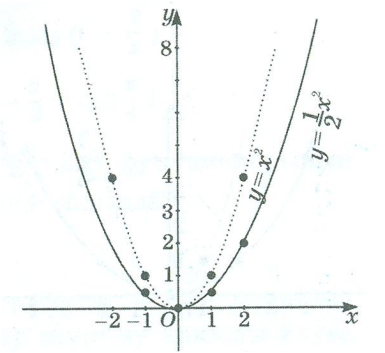
ІІ. y=kf(x) функциясының графигін салу үшін y=f(x) функциясының графигін Оу осінің бойымен 
болғанда, 
есе созу, 
болғанда 
–ға сығу (қысу) керек.
2-мысал. а )
ә)
функцияларының графигін салайық.
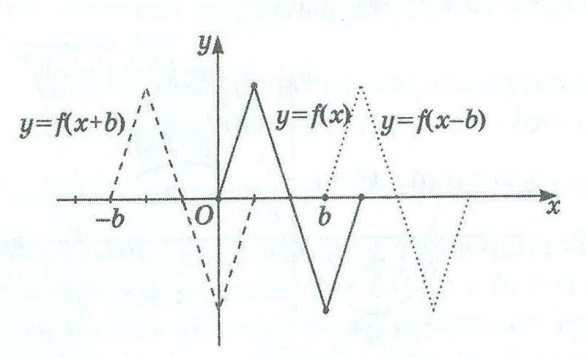
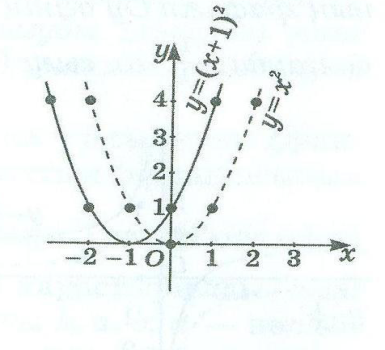
ІІІ. y=f(x+b) функциясының графигін y=f(x) функциясының графигінен Ох осінің бойымен b0 болғанда, теріс бағытта, b бірлікке параллель көшіру арқылы алуға болады.
3-мысал. 
функциясының графигін салайық.
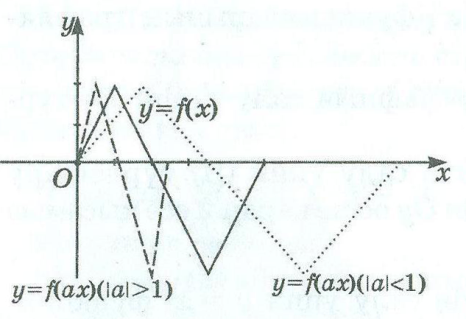
ІV. y=f(ax) функциясының графигін y=f(x) функциясының графигінен Ох осі бойымен
болғанда, 
есе рет сығу немесе 
болғанда, 
есе рет созу арқылы алады.
4-мысал. а) y=(1/2x)2 ,ә) 
функцияларының графигін салайық.
V. y=kf(ax+b)+d фуркциясының графигін салу үшін жоғарыда қарастырылған түрлендірудің төртеуін қолдану керек.
5-мысал. функциясының графигін салайық.
Тапсырмалар:
№1
1) f(x)=3x2-1, x=-2;4.5;1/3
2) f(x)=x3, x=-1;1/2;2 - х-тің мәнін қойып функция мәнін тап.
№2
Қарапайым түрлендірулер қолдану арқылы y=f(x) функциясының графигін салыңдар.
1) y=-3(x-4)2-1
2) y=2(x2-1)
3) y=
x2+5
Жеке тапсырма:
y=x2 функциясының графигін қолдана отырып y=-3x2+12x+8 функциясының графигін салу үшін қандай түрлендірулер орындау қажет?
Сандық функция. Функцияның берілу тәсілдері, функциялардың графигтерін қарапайым түрлендіру. (2.52 MB)
0
665
1
Нравится
0
