1 вариант.
Используя правило многоугольника, упростите выражение
![]()
Постойте не нулевой вектор а, и вектор равный 2а, -2,5а, -4а.
М, Н, О, Р, S – произвольные точки. Найти сумму
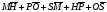 .
.
Начертите параллелограмм ABCD и постройте векторы
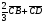 ,
, 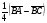 .
.Найти четырьмя разными способами сумму следующих векторов.
2 вариант.
Используя правило многоугольника, упростите выражение
![]()
Постойте не нулевой вектор а, и вектор равный -а, -1,5а, 4а.
А, В, С, D, Е – произвольные точки. Докажите, что
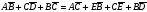 .
.Начертите треугольник АВС и постройте векторы
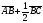 и
и 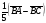
Найти четырьмя разными способами сумму следующих векторов.
вариант.
Используя правило многоугольника, упростите выражение
![]()
Постойте не нулевой вектор а, и вектор равный 2а, -2,5а, -4а.
М, Н, О, Р, S – произвольные точки. Найти сумму
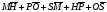 .
.
Начертите параллелограмм ABCD и постройте векторы
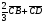 ,
, 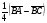 .
.Найти четырьмя разными способами сумму следующих векторов.
вариант.
Используя правило многоугольника, упростите выражение
![]()
Постойте не нулевой вектор а, и вектор равный -а, -1,5а, 4а.
А, В, С, D, Е – произвольные точки. Докажите, что
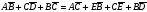 .
.Начертите треугольник АВС и постройте векторы
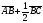 и
и 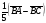
Найти четырьмя разными способами сумму следующих векторов.
1 вариант.
М, Н, О, Р, S – произвольные точки. Найти сумму
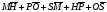 .
.
В параллелограмме ABCD диагонали пересекаются в точке М. Докажите, что
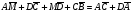 .
.Найти четырьмя разными способами сумму следующих векторов.
2 вариант.
А, В, С, D, Е – произвольные точки. Докажите, что
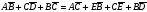 .
.
ABCD – прямоугольник. Диагонали его пересекаются в точке О. Докажите, что
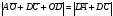 .
.Найти четырьмя разными способами сумму следующих векторов.
1 вариант.
М, Н, О, Р, S – произвольные точки. Найти сумму
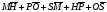 .
.
В параллелограмме ABCD диагонали пересекаются в точке М. Докажите, что
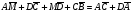 .
.Найти четырьмя разными способами сумму следующих векторов.
2 вариант.
А, В, С, D, Е – произвольные точки. Докажите, что
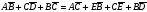 .
.
ABCD – прямоугольник. Диагонали его пересекаются в точке О. Докажите, что
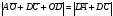 .
.Найти четырьмя разными способами сумму следующих векторов.
1 вариант.
В прямоугольнике ABCD AD=12, CD=5, О – точка пересечения диагоналей. Найти
.
Дан треугольник АВС. Постройте вектор
.
На стороне ВС параллелограмма ABCD взята точка К так, что ВК:КС=1:4. Выразите векторы
и
через векторы
и
.
(*)Даны параллелограмм ABCD и произвольная точка О. Выразите вектор
через векторы
,
,
.
2 вариант.
В ромбе ABCD AD=20, ВD=24, О – точка пересечения диагоналей. Найти
.
Дан треугольник АВС. Постройте вектор
.
На стороне НК ромба МНКС взята точка Е так, что КЕ=0,2НЕ. Т – середина стороны МН. Выразите векторы
и
через векторы
и
.
(*)В четырехугольнике ABCD выполняется
, где О – произвольная точка плоскости. Докажите, что ABCD – параллелограмм.
1 вариант.
В прямоугольнике ABCD AD=12, CD=5, О – точка пересечения диагоналей. Найти
.
Дан треугольник АВС. Постройте вектор
.
На стороне ВС параллелограмма ABCD взята точка К так, что ВК:КС=1:4. Выразите векторы
и
через векторы
и
.
(*)Даны параллелограмм ABCD и произвольная точка О. Выразите вектор
через векторы
,
,
.
2 вариант.
В ромбе ABCD AD=20, ВD=24, О – точка пересечения диагоналей. Найти
.
Дан треугольник АВС. Постройте вектор
.
На стороне НК ромба МНКС взята точка Е так, что КЕ=0,2НЕ. Т – середина стороны МН. Выразите векторы
и
через векторы
и
.
(*)В четырехугольнике ABCD выполняется
, где О – произвольная точка плоскости. Докажите, что ABCD – параллелограмм.
1 вариант.
В прямоугольнике ABCD AD=12, CD=5, О – точка пересечения диагоналей. Найти
.
Дан треугольник АВС. Постройте вектор
.
На стороне ВС параллелограмма ABCD взята точка К так, что ВК:КС=1:4. Выразите векторы
и
через векторы
и
.
(*)Даны параллелограмм ABCD и произвольная точка О. Выразите вектор
через векторы
,
,
.
Самостоятельная работа по теме «Умножение вектора на число, вычитание векторов.»
2 вариант.
В ромбе ABCD AD=20, ВD=24, О – точка пересечения диагоналей. Найти
.
Дан треугольник АВС. Постройте вектор
.
На стороне НК ромба МНКС взята точка Е так, что КЕ=0,2НЕ. Т – середина стороны МН. Выразите векторы
и
через векторы
и
.
(*)В четырехугольнике ABCD выполняется
, где О – произвольная точка плоскости. Докажите, что ABCD – параллелограмм.
1 вариант.
В прямоугольнике ABCD AD=12, CD=5, О – точка пересечения диагоналей. Найти
.
Дан треугольник АВС. Постройте вектор
.
На стороне ВС параллелограмма ABCD взята точка К так, что ВК:КС=1:4. Выразите векторы
и
через векторы
и
.
(*)Даны параллелограмм ABCD и произвольная точка О. Выразите вектор
через векторы
,
,
.
2 вариант.
В ромбе ABCD AD=20, ВD=24, О – точка пересечения диагоналей. Найти
.
Дан треугольник АВС. Постройте вектор
.
На стороне НК ромба МНКС взята точка Е так, что КЕ=0,2НЕ. Т – середина стороны МН. Выразите векторы
и
через векторы
и
.
(*)В четырехугольнике ABCD выполняется
, где О – произвольная точка плоскости. Докажите, что ABCD – параллелограмм.
Самостоятельная работа по теме «Умножение вектора на число, вычитание векторов.»
1 вариант.
В прямоугольнике ABCD AD=12, CD=5, О – точка пересечения диагоналей. Найти
.
Дан треугольник АВС. Постройте вектор
.
На стороне ВС параллелограмма ABCD взята точка К так, что ВК:КС=1:4. Выразите векторы
и
через векторы
и
.
(*)Даны параллелограмм ABCD и произвольная точка О. Выразите вектор
через векторы
,
,
.
2 вариант.
В ромбе ABCD AD=20, ВD=24, О – точка пересечения диагоналей. Найти
.
Дан треугольник АВС. Постройте вектор
.
На стороне НК ромба МНКС взята точка Е так, что КЕ=0,2НЕ. Т – середина стороны МН. Выразите векторы
и
через векторы
и
.
(*)В четырехугольнике ABCD выполняется
, где О – произвольная точка плоскости. Докажите, что ABCD – параллелограмм.
Контрольная работа по теме «Векторы».
1 вариант.
Начертите параллелограмм ABCD и постройте векторы
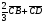 ,
, 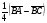 .
.В треугольнике АВС
- середина АС, М – точка пересечения медиан.
Выразите
через
и
.
Выразите
через
и
.
3) Выразите через
и
, если точка
лежит на ВС, причем
.
Используя векторы, докажите, что середина отрезка
лежит на прямой
, если
и
.
Контрольная работа по теме «Векторы».
2 вариант.
Начертите треугольник АВС и постройте векторы
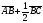 и
и 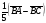 .
.Основания ВС и AD трапеции ABCD относятся как 1:2, Е – середина стороны CD, О – точка пересечения диагоналей.
Выразите
через
и
.
Выразите
через
и
.
Выразите
через
и
.
4) Используя векторы, докажите, что точка М, делящая отрезок АЕ в отношении 1:4, считая от точки Е, принадлежит прямой BD.
Контрольная работа по теме «Векторы».
1 вариант.
1. Начертите параллелограмм ABCD и постройте векторы 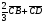 ,
, 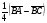 .
.
2.В треугольнике АВС - середина АС, М – точка пересечения медиан.
Выразите
через
и
.
Выразите
через
и
.
3) Выразите через
и
, если точка
лежит на ВС, причем
.
4)Используя векторы, докажите, что середина отрезка лежит на прямой
, если
и
.
Контрольная работа по теме «Векторы».
2 вариант.
1. Начертите треугольник АВС и постройте векторы 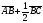 и
и 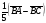 .
.
2.Основания ВС и AD трапеции ABCD относятся как 1:2, Е – середина стороны CD, О – точка пересечения диагоналей.
Выразите
через
и
.
Выразите
через
и
.
Выразите
через
и
.
4) Используя векторы, докажите, что точка М, делящая отрезок АЕ в отношении 1:4, считая от точки Е, принадлежит прямой BD.

 Получите свидетельство
Получите свидетельство Вход
Вход












 Самостоятельная работа по теме Вектор для 9 класса (150.72 KB)
Самостоятельная работа по теме Вектор для 9 класса (150.72 KB)
 0
0 23951
23951 1479
1479 Нравится
0
Нравится
0


