Решение уравнений

Модуль «АЛГЕБРА» №4

Решение уравнений

• Цель урока: Создание условий для представления учащимися целостной картины темы  «Решение уравнений».

• Образовательные задачи:
• ━  повторить виды уравнений и способы их решения;
• ━  способствовать восполнению существующих пробелов в знаниях    учащихся
• ━  помочь учащимся систематизировать знания по данной теме.
• Развивающие задачи:
• ━  развивать мыслительную деятельность;
• ━  развивать информационную компетенцию учащихся;
• ━ способствовать проявлению познавательной активности учащихся.
• Воспитательные задачи:
• ━  воспитывать культуру умственного труда;
• ━  воспитывать культуру речи.

Линейные уравнения: аx+b=0

Квадратные уравнения: ax 2 +bx+c=0

Дробно – рациональные уравнения:

Реши устно

-6+3 -25+5

-5+(-4) -18+(-12)

-8+3 -7+3

9+(-6)

-2+(-8)

-15+5

6-10

-15-3

18-(-2)

34-38

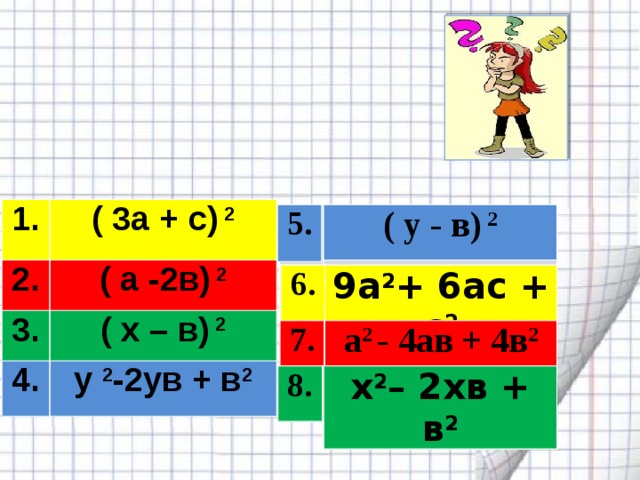
Соедините пары

тождественно равных выражений

1.

2.

( 3а + с) 2

( а -2в) 2

3.

( x – в) 2

4.

y 2 -2yв + в 2

( y - в) 2

5.

( y - в) 2

5.

9а 2 + 6ас + с 2

6.

9а 2 + 6ас + с 2

6.

7.

а 2 - 4ав + 4в 2

а 2 - 4ав + 4в 2

7.

8.

x 2 – 2xв + в 2

8.

x 2 – 2xв + в 2

x 2 – 2xв + в 2

8.

ЛИНЕЙНЫЕ

УРАВНЕНИЯ

Определение: уравнение вида а х = в (где х – переменная, а и в – некоторые числа) называется линейным уравнением с одной переменной.

Отличительная особенность такого уравнения – переменная х входит в уравнение обязательно в первой степени.

Уравнение вида ах=в ,где х переменная,а и в некоторые числа называется линейным уравнением с одной переменной.

• Алгоритм (решения линейных уравнений)
• 1. Раскрыть скобки в каждой части уравнения (если нужно).
• 2. Неизвестные собрать в левой части уравнения, известные в правой части уравнения. ( При переносе слагаемых из одной части уравнения в другую знак «+» меняем на “ –“,а знак “ – “ на «+».)
• 3. В каждой части уравнения приведи подобные слагаемые.
• 4. Неизвестное найди, как неизвестный множитель ( произведение подели на известный множитель).

Сколько корней может иметь

линейное уравнение ax=-b ?

Реши устно

2х=18 0х=5

-4х=20 0х=0

6х=-36 -3х=27

-8х=-64 8х=32

Реши в тетради и расскажи другу

1) -4х+8=-8

2) 9х+6=10х

3) -1+2х=10х+3

4) 7(-3+2х)=-6х-1

5) х-3(1-7х)=2х+2

Реши в тетради и расскажи другу

1) -4х+8=-8 ; х=4

2) 9х+6=10х ; х=6

3) -1+2х=10х+3; х=0,5

4) 7(-3+2х)=-6х-1; х=1

5) х-3(1-7х)=2х+2 ; х=0,25

Квадратные уравнения

ax 2 +bx+c=0

Квадратные уравнения:

Неполные квадратные уравнения:

ax 2 +c=0

ax 2 +bx=0

x(ax+b)=0

x=

x=0 или (ax+b)=0

x=-b:a

где ас

Неполные квадратные уравнения

х 2 -8х=0

2х 2 -18=0

Неполные квадратные уравнения:

Проверка

• 1. х=0 х=-5
• 2. х=о х=4,5
• 3. х=0 х=12
• 4.х=0 х=5\3
• 5.нет корней
• 6.х=2 х=-2
• 7.х=3 х=-3
• 8. нет корней

Видеоролик «Квадратные уравнения»

Квадратные уравнения

Решите уравнение:

Решение:

х = 0,5 и х = - 5.

Ответ: ___________

Квадратный трехчлен разложен на множители. Найдите а.

Разложение на множители

Трехчлен ax 2  + bx + c, имеющий корни x 1  и x 2 , можно разложить на множители по следующей формуле:

a(x – x 1 )(x – x 2 ).

Чтобы найти корни квадратного трехчлена  ax 2  + bx + c , надо приравнять его к нулю - то есть решить квадратное уравнение  ax 2  + bx + c =  0

Разложим на множители трехчлен 2 x 2  + 7x – 4. Мы видим: коэффициент  а  = 2. Теперь найдем корни трехчлена. Для этого приравняем его к нулю и решим уравнение 2 x 2  + 7x – 4 = 0.

• Наш трехчлен имеет два корня: x 1  = 1/2, x 2  = –4.

Подставим в нашу формулу значения корней, вынеся за скобки значение коэффициента  а , и получим:

2x 2  + 7x – 4 = 2(x – 1/2) (x + 4).

Полученный результат можно записать иначе, умножив коэффициент 2 на двучлен  x  – 1/2:

2x 2  + 7x – 4 = (2x – 1) (x + 4).

Квадратный трехчлен разложен на множители. Найдите а.

Квадратный трёхчлен разложен на множители. Найдите значение а.

• Х 2 +6х-27=(х+9)(х-а)

Разложите на множители квадратный трехчлен

Самостоятельная работа для учащихся 1 группы

Ответы к самостоятельной работе для взаимопроверки.

• 1. х=6
• 2. х=0,5 х=1
• 3. х=-9 х=2
• 4. х=22
• 5. х=-3
• 6.х=-3 х=6
• 7. х=0 х=-4
• 8. х=1,5
• 9. х=2 х=-8
• 10. х=0 х=-4

Задания для учащихся 2-ой группы

Просмотри видеоролик и реши уравнение видеоролик

Модуль «Алгебра»

Задание 21

Решите уравнение

• 1.Чем данный урок был полезен для вас?

• 2.Какие пробелы в знаниях помог восполнить?

Дома

• 1группа-ОГЭ-2016
• вариант 12-20 задание 4
• 2 группа ОГЭ-2016
• Вариант12-15 задание 4
• Вариант 22,25,26

задание 21