Тема: «Решение уравнений в 7 классе».
Составил учитель математики:
Супрунова Н. В. МБОУ СОШ № 29 г. Хабаровск
УМК - Макарычев Ю.Н. «Алгебра 7 класс».
Изучение темы «Уравнения с одной переменной» происходит в 7 классе на новом витке. По сравнению с 6-ым классом усиливается роль теории с целью обеспечения осознанного восприятия учащимися алгоритма решения уравнений. Вводятся важные определения, связанные с понятием уравнения, которые распространяются на уравнения любого вида, и в дальнейшем будут неоднократно использоваться. Исследуется вопрос о числе корней уравнения. Особое внимание уделяется решению уравнений вида «ах=в» при различных значениях коэффициентов «а» и «в», а также несложных уравнений, сводящихся к линейным уравнениям.
Цель: учащиеся будут уметь оценивать степень усвоения алгоритма решения уравнений с одной переменной в его применении для решения уравнений как минимум вида «ах=в», и как максимум уравнений, содержащих знак модуля и параметр.
Задачи:
-организовать самоконтроль учащихся по овладению основными понятиями темы «уравнение с одной переменной»,
-организовать взаимоконтроль учащихся по умению применять алгоритм решения уравнения первой степени с одним неизвестным,
-создать условия для возможности формирования универсальных учебных действий общения и сотрудничества с одноклассниками при решении уравнений как минимум вида «ах=в» и как максимум уравнений, содержащих модуль и параметр посредством интерактивной работы в группах,
- создать условия для развития творческого потенциала и интеллектуальных возможностей учащихся путём включения в классную и домашнюю работу нестандартных заданий.
Оборудование: мел, доска, проектор, раздаточный материал.
Ход урока
I. Вводная часть
Цель: учащиеся будут уметь проводить самооценку уровня усвоения основных теоретических положений и умения их применять к решению линейных уравнений, как следствие – создание мотивации на урок.
Реализуется: через самостоятельную работу, индивидуальную работу по составлению интеллект - карты зависимости числа корней уравнения от коэффициентов «а» и «в» и заполнение листа самооценки.
| Этапы урока | Деятельность учителя | Приращение в опыте ученика |
| I. Вводная часть | Организация самоконтроля ученика по овладению основными понятиями: линейное уравнение, корень уравнения, что значит решить уравнение, свойства уравнений, равносильные уравнения, от чего зависит количество корней линейного уравнения | Отличать линейное уравнение от других видов уравнений, классифицировать уравнение по количеству решений и оценивать свои умения |
Задания
Самостоятельная работа:
1.Какие из данных уравнений относятся к линейным уравнениям или уравнениям, сводящимся к линейным?
1. 0х=0
2. 2х – 5=3х – 4
3. 3х²=12
4. -10=5х – 2,5
5. Х +У - 9=0
6. 0,6а+2=12
7. х/3=6
8. 5х³+1= -6
9. У (У+1)=0
10. 2 - 2Х= -2х + 3
11. Х+3=5 + Х – 2
12. 5У-У=5У+4
Учащиеся выписывают в тетрадь номера уравнений, сверяют свои ответы с верными ответами на экране и заполняют первую строку листа самооценки.
Лист самооценки ученика
Класс: 7
ФИО:
Предмет: алгебра
Тема: линейное уравнение с одной переменной
| № | Виды работ | Отл. | Хор. | Мог бы лучше |
| 1 | Распознавание линейных уравнений и уравнений, сводящихся к линейным |
|
|
|
| 2 | Знание и понимание понятийного аппарата |
|
|
|
| 3 | Умение определять количество корней уравнения |
|
|
|
| 4 | Умение применять алгоритм сведения уравнения с одной переменной к линейному (оценивает напарник) |
|
|
|
| 5 | Умение выполнять нестандартные задания |
|
|
|
| 6 | Работа в группах |
|
|
|
| 7 | Решение теста |
|
|
|
2. Знание и понимание понятийного аппарата.
Ученикам предлагается собрать пазл, содержащий ответ на один из вопросов:
- какое уравнение называется линейным уравнением с одной переменной?
-что называется корнем уравнения?
-что значит решить уравнение?
-какими свойствами обладают уравнения?
- какие уравнения называют равносильными?
- от чего зависит количество корней уравнения вида « ах=в»?
Правильность собранного пазла проверяют в ходе обсуждения. Заполняют вторую строку в листе самооценки.
3. Умение определять количество корней уравнения.
а) Индивидуальная работа по созданию интеллект – карты (хорошо успевающим ученикам)
«Зависимость количества решений уравнения а∙х = в от коэффициентов».
| ах=в |


|
|



|
|
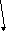
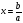 |


| множество решений |
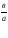
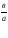
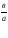
б) Остальные ученики выполняют задания по рядам (используя уравнения задания №1).
Задание 1 ряду.
Выписать уравнения, имеющие один корень.
Составьте свое уравнение, имеющее один корень.
Задания 2 ряду.
Выписать уравнения, имеющие множество корней.
Составьте свое уравнение, имеющее множество корней.
Задание 3 ряду.
Выписать уравнения, не имеющие корней.
Составьте свое уравнение, не имеющее корней.
Учащиеся выписывают в тетрадь номера уравнений, сверяют свои ответы с верными ответами, выведенными на экран. Составленные уравнения выборочно выписываются на классной доске и обсуждается правильность их составления. Аналогично, ученики, работающие индивидуально, сверяют с интеллект-картой, выведенной на экран, правильность выполнения задания. Заполняют строку №3 листа самооценки.
II. Основная часть
Цель: учащиеся будут уметь взаимооценивать правильность применения алгоритма решения уравнений первой степени с одним неизвестным, получат возможность выявлять пробелы, оказывать взаимопомощь, выстраивать личный образовательный вектор на урок, развить познавательную активность.
Реализуется: путём организации самостоятельной работы, работы в парах, решения нестандартного задания и заполнения листа самооценки.
| Этапы урока | Деятельность учителя | Приращение в опыте ученика |
| II. Основная часть | I. Организация работы в парах для проведения взаимоконтроля по умению применять алгоритм решения уравнения первой степени с одним неизвестным
| Применять алгоритм решения уравнений первой степени с одним неизвестным и оценивать уровень умений напарника по применению им данного алгоритма |
| II. Организация поисково-исследовательской деятельности учащихся с целью совершенствования умений выполнять нестандартные задания | Выявление уровня владения умением решать нестандартные задания и постановка задач по совершенствованию | |
| III. Проведение физкультминутки для снятия напряженности и усталости | Выполняют физические упражнения |
I Задание.
а) Собери пазл «Алгоритм решения уравнения».
Ученики выполняют взаимопроверку задания в парах, используя текст алгоритма из учебника.
Учитель предлагает учащимся образец решения уравнения по алгоритму на слайде.
2(3 х-1) = 4(х + 3)+2х
1. Раскроем скобки:
6х - 2= 4х+ 12+ 2х
2. Рассортируем:
6х - 4 х-2х= 2+12
3. Приведём подобные:
0х=14 , где а=0, в=14.
4.Очевидно, что при подстановке любого значения «х» получаем неверное числовое равенство 0=14.
Поэтому уравнение корней не имеет.
б) Работа в парах.
Решить уравнение 12-(4х-18)=(36+4х)+(18-6х) в своих тетрадях, обменяться тетрадями с соседом по парте, проверить работу друг друга.
На доске (закрытая информация)
1.Раскрываем скобки
12-4х+18=36+4х+18-6х
2.Переносим слагаемые с переменной в левую часть уравнения, а слагаемые без переменной – в правую часть уравнения, изменив при этом их знаки.
-4х-4х+6х=36+18-18-12
3.Приведем подобные.
-2х=24
4.Находим корень уравнения.
х=24:(-2)
х=-12
Ученики заполняют строку №4 листа самооценки.
II.Задание (мозговой штурм).
1. Найди корень уравнения 3х+5=7х-11.
2. Если я уберу два числа 5 и 7,то получу запись 3х + …=…∙х - 11.
Внимание. Запиши вместо убранных чисел такие числа, чтобы новое полученное уравнение имело корень 5.
3. «Если не получилось, не переживай, попробуй к этому заданию вернуться дома».
Ученики заполняют 5 строку в листе самооценки.
III. Физкультминутка.
III.Обобщающая часть.
Цель: ученик получит возможность совершенствовать навык решения уравнений с одной переменной, развить умение общаться, сотрудничать со сверстниками, оценивать свою работу в группе.
Реализация: групповая работа по выполнению дифференцированного задания, заполнение листа самооценки.
| Этапы урока | Деятельность учителя | Приращение в опыте ученика |
| III. Обобщающая часть | Организация интерактивной работы в группах для обеспечения формирования универсальных учебных действий: общения и сотрудничества со сверстниками при решении как минимум линейного уравнения вида «ах=b» и как максимум уравнений, содержащих модуль и параметр | Ученик сможет приобрести опыт общения и сотрудничества со сверстниками при обсуждении приемов решения предложенных уравнений. Получит возможность проявить свои способности при решении как минимум линейного уравнения вида «ах=b» и как максимум уравнений, содержащих модуль и параметр и оценить правильность решения уравнений различной степени сложности. |
Задание.
Работа в группах.
Реши уравнения:
1. 5х=45 (1 б.)
2. 5+2у=45 (1 б.)
3. 3(у-8)=6у-54 (2 б.)
4. Вырази из формулы J=U/R букву U. (2б.)
5. Реши уравнение │х+3│=15 (3 б.)
6. При каком значении « а» уравнение
(4а-1)∙х=1+16а имеет корень, равный 5? (3 б.)
3-4 б. - «3»
5-7 б. – «4»
8-12 б. – «5»
Группам выдаются карточки – подсказки для решения уравнения №5:
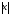 =4, х=-4, х=4
=4, х=-4, х=4
По завершению работы, группы проверяют правильность решения, сверяя свои ответы с верными ответами, выведенными на экран. Учитель подводит итоги работы групп. Учащиеся оценивают своё участие в работе группы в листе самооценки.
IV. Заключительная часть.
Цель: ученик получит возможность выявить уровень умения решать линейные уравнения, уравнения с одной переменной, сводящиеся к линейным и уравнения, содержащие модуль и параметр, а также умения оценивать себя.
Реализуется: путём проведения дифференцированной тестовой работы и заполнения листа самооценки.
| Этапы урока | Деятельность учителя | Приращение в опыте ученика |
| IV. Заключительная часть | I. Организация самооценивания учащихся по достижению цели урока посредством тестирования. | Оценивание уровня личных достижений цели урока |
| II. Напоминание о творческом домашнем задании: создание буклета по теме «Уравнение с одной переменной» и решении нестандартного задания по подбору коэффициентов уравнения. |
|
Задание.
а) Реши тест.
Тест:
Какое из чисел является корнем уравнения?
-3х=27 а) -7; б) -9; в) 9; г) -81. (1 б.)
5х+5=2х-7 а) 4; б) 1; в) 5; г) -4. (1 б.)
5х – (х-3)=5 а) 1,5; б) -2; в) 2; г) 0,5. (2 б.)
│х+4│=8 а) 4и-12; б) -4и12; в) 5и-12; г) 4. (3 б.)
При каком значении «с» уравнение сх = 5 не имеет корней?
а) 1; б) 0; в) 5; г) -5. (3 б.)
«3» - 2 - 4 б.
«4» - 5 – 7 б.
«5» - 8- 10 б.
По завершению работы, учащиеся проверяют правильность решения, сверяя свои ответы с верными, выведенными на экран. Заполняют лист самооценки.
б) Домашнее задание.
Учитель напоминает о творческом домашнем задании: создание буклета по теме «Уравнение с одной переменной» и решении нестандартного задания по подбору коэффициентов уравнения из «Мозгового штурма».
В конце урока учитель собирает тетради учащихся с домашней и классной работой и листы самооценки. На основании листов самооценки и проверенных работ учитель выставляет учащимся оценки за урок.
Используемая литература:
1.Учебник «Алгебра-7класс», авт. Ю.Н.Макарычев.
2.Дидактический материал «алгебра-7 класс», под ред. Л.И.Звавича.
3. «Занимательные задания в обучении математике» М.Ю.Шуба.
Анализ урока.
Урок рассчитан на общеобразовательный класс. Структура урока соответствует программе, поставленной цели, уровню подготовки учащихся.
Цель урока сформулирована исходя из потребностей ученика: уметь как минимум оценивать правильность применения алгоритма к решению уравнений с одной переменной вида «ах=в», и как максимум уравнения, содержащие знак модуля и параметр. Задачи урока сформулированы исходя из действий учителя, необходимых для обеспечения целей, поставленных учеником.
Соблюдены гигиенические требования к уроку: есть динамическая пауза. В течение урока учитель следит за осанкой учащихся и при необходимости делает им замечания.
Создана ситуация успеха: в листах самооценки вместо «3» и «2» написано: «Мог бы лучше». Предусмотрена творческая работа, как на уроке, так и при выполнении домашнего задания.
На каждом этапе урока ученик анализирует свою деятельность и оценивает её, что позволяет ему ставить перед собой задачи, выстраивая свою образовательную траекторию.
Цель урока достигается через применение различных технологий: технологию сотрудничества (учитель- ученик), технологию индивидуализации обучения (оказание индивидуальной помощи со стороны учителя и одноклассников), технология развивающего обучения, групповые формы работы, дифференцированное обучение, личностно- ориентированная технология, технология интерактивного обучения. Ведущей технологией является технология формирующего оценивания деятельности.
Урок соответствует системно - деятельностному подходу в обучении, способствует проявлению самостоятельности на репродуктивном и творческом уровне, активности, а также продвижению в умственном развитии. Учащиеся вырабатывают навык поведения при работе в парах и группами: учебное сотрудничество, умение договориться, распределять работу, оценивать свой вклад в результат общей деятельности, соревнование между группами. Каждый этап урока способствует возможности формирования универсальных учебных действий: личностных, регулятивных, познавательных, коммуникативных. На уроке предполагается непосредственная индивидуальная помощь учащимся со стороны учителя и одноклассников и опосредованная с помощью карт- подсказок.
Учащиеся на уроке получили возможность научиться контролировать и самооценивать свою деятельность, самостоятельно находить и исправлять ошибки, определять степень успешности.

 Получите свидетельство
Получите свидетельство Вход
Вход


 а≠0
а≠0
 в=0
в=0








 Решение уравнений (64.86 KB)
Решение уравнений (64.86 KB)
 0
0 736
736 13
13 Нравится
0
Нравится
0









