Решение треугольников

Решение треугольников

Урок 1

Задачи урока:

• Повторить теорему о площади треугольника, теоремы синусов и косинусов;
• Научиться применять теоремы к решению треугольников;
• Научиться выбирать метод решения треугольника по заданным условиям.

Повторение:

• Сформулируйте теорему синусов;
• Запишите формулу, выражающую теорему синусов.
• Сформулируйте теорему косинусов;
• Запишите формулу, выражающую теорему косинусов.
• Запишите теорему косинусов для двух других сторон.
• Выразите из формулы теоремы косинусов косинус угла.

Теорема синусов

Стороны треугольника пропорциональны синусам противоположных углов.

Теорема косинусов

Квадрат стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.

Теорема косинусов

Решить задачу:

B

Дано: a, b, C

Найти: с, A, B

a

Решение:

1. по теореме косинусов

A

b

C

2. по теореме синусов

3. Откуда:

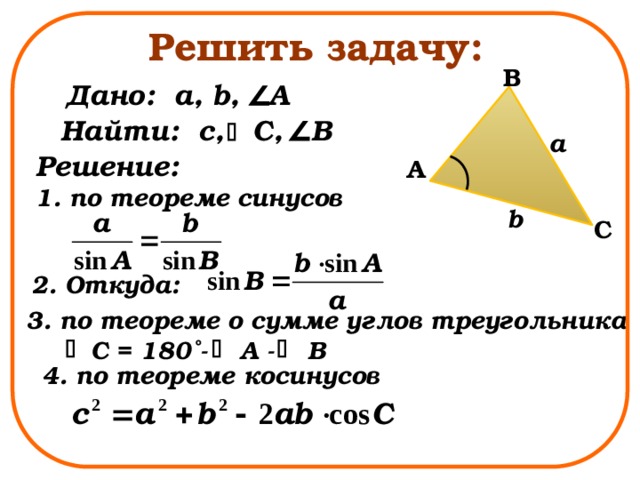
Решить задачу:

B

Дано: a, b, A

Найти: с, C, B

a

Решение:

1. по теореме синусов

A

b

C

2. Откуда:

3. по теореме о сумме углов треугольника

C = 180˚- A - B

4. по теореме косинусов

Решить задачу:

B

Дано: a, b, c

c

Найти: C, A, B

a

Решение:

1. по теореме косинусов

A

b

C

2. по теореме косинусов

3. по теореме о сумме углов треугольника

C = 180˚- A - B

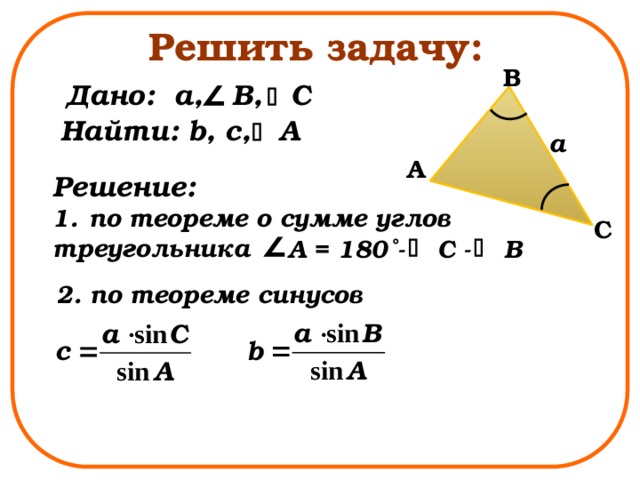
Решить задачу:

B

Дано: a, B, C

Найти: b, с, A

a

A

Решение:

• по теореме о сумме углов

треугольника

C

A = 180˚- C - B

2. по теореме синусов

Решить задачи:

№№ 116, 118, 120

Самостоятельно:

Найдите неизвестные стороны и углы треугольника ABC, если:

1)

2)

3)

4)

AC = 8 см, ∠B = 48° , ∠C = 56°;

AB = 4 см, BC = 5 см, ∠B = 110°;

AB = 4 см, BC = 6 см, ∠A = 100°;

AB = 8 см, BC = 9 см, ∠A = 40°.

Дома:

№№ 117, 119, 121.

Знать теорию, задачи