Решение треугольников.

РЕШЕНИЕ ТРЕУГОЛЬНИКОВ «ТЕОРЕМА СИНУСОВ» «ТЕОРЕМА КОСИНУСОВ»

Ты узнаешь:

• как применять теоремы синусов и косинусов для решения треугольников и прикладных задач.

Ты научишься:

• применять теоремы синусов и косинусов для решения треугольников и прикладных задач.

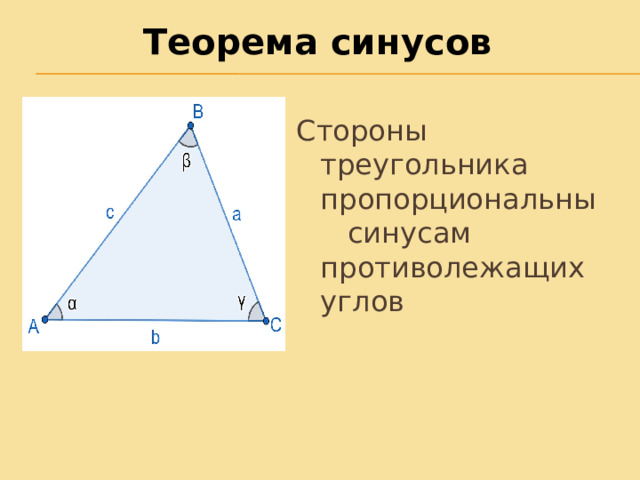
Теорема синусов

Стороны треугольника пропорциональны синусам противолежащих углов

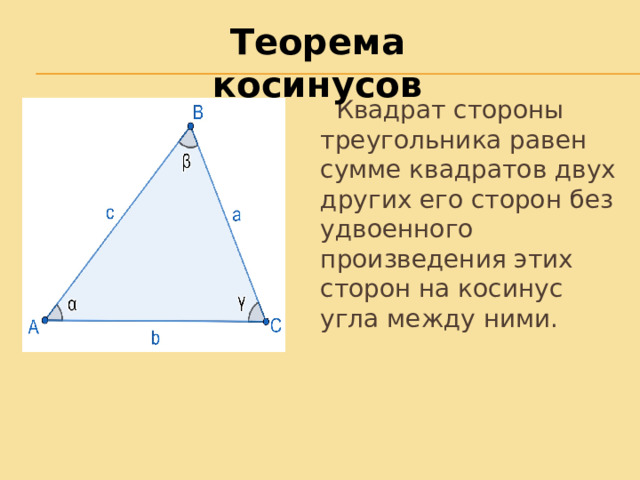
Теорема косинусов

Квадрат стороны треугольника равен сумме квадратов двух других его сторон без удвоенного произведения этих сторон на косинус угла между ними.

Следствие 1 из теоремы косинусов.

Для определения косинуса углов треугольника используются формулы:

, .

Следствие 2 из теоремы косинусов.

если , то угол – острый,

если , то угол – прямой,

если , то угол – тупой.

Следствие из теоремы синусов. .

С помощью данных теорем можно решить произвольный треугольник по трем основным элементам.

Задачи

4.      Смежные стороны параллелограмма равны 7 см и 8 см, а угол между ними равен 120 0 . Найти диагонали параллелограмма и его площадь.