Решение прототипов задания №21 части 2 ОГЭ – системы уравнений

Способы решения систем уравнений с двумя переменными : * способ подстановки, * способ алгебраического сложения, * способ замены или введения новой переменной.

Решением системы уравнений с двумя переменными называется множество пар в данном случае Х и У, при котором каждое из уравнений превращается в верное равенство.

Решение Решение. Решим первое уравнение и подставим его решение во 2-ое уравнение. Произведение двух сомножителей равно нулю. Оно равно нулю тогда и только тогда, когда хотя бы один из сомножителей равен нулю. А это значит, что 1-ое уравнение равносильно совокупности Получаем две новые системы: 1. 1-ая система не имеет решения. 2. Решение системы уравнений: (3;6). Ответ : ( 3;6).

2)

Решение ( способ подстановки)

Во 2-ое уравнение системы подставим (2х+3) 2 из 1-ого уравнения системы.

Решим полученное уравнение : (3х+2) 2 = (2х+3) 2

(3х+2) 2 – (2х+3) 2 =0

По формуле разности квадратов : ( 3х+2 - 2х-3)(3х+2+2х+3) = 0

( х – 1)(5х+5) = 0

х-1 = 0 или 5х+5 = 0

х=1 х= -1

Если х=1, то ( 2·1+3) 2 = 5у , 5у = 25, у=5.

Если х = -1 , то ( 2·(-1) +3) = 5у, 5у = 1, у = 0,2.

Решения системы уравнений : ( -1;0,2), (1;5).

Ответ: ( -1;0,2), (1;5).

3) 3х 2 +у = 4,

2х 2 – у =1.

Решение ( способ алгебраического сложения)

Почленно сложим уравнения системы.

Решим полученное уравнение : 5х 2 = 5

х 2 = 1

х = 1 и х = -1

Если х = 1, то 2 · 1 2 – у = 1 , у = 1.

Если х = -1 , то 2 · (-1) 2 – у = 1 , у = 1.

Решения системы : ( -1;1), ( 1;1).

Ответ: ( -1;1), ( 1;1).

Оформление :

4)

Решение ( способ замены или введения новой переменной)

Пусть

Получим систему линейных уравнений: 3а – 4в =1,

2а + 5в = 4,5.

Решим систему линейных уравнений способом алгебраического сложения.

Если а=1, то , х=1.

Если в=0,5, то , у=2.

Решение системы : (1;2).

Ответ: (1;2).

5)

Решение

Решения системы уравнений : (2;-5), (5;-2).

Ответ: (2;-5), (5;-2).

6)

Решение

Решения системы уравнений: (0;0) , (

Ответ: (0;0) , (

7)

Решение

1 случай: х≥0.

2 случай: х˂0.

Решение системы уравнений: (-3;-5).

Ответ: (-3;-5).

.

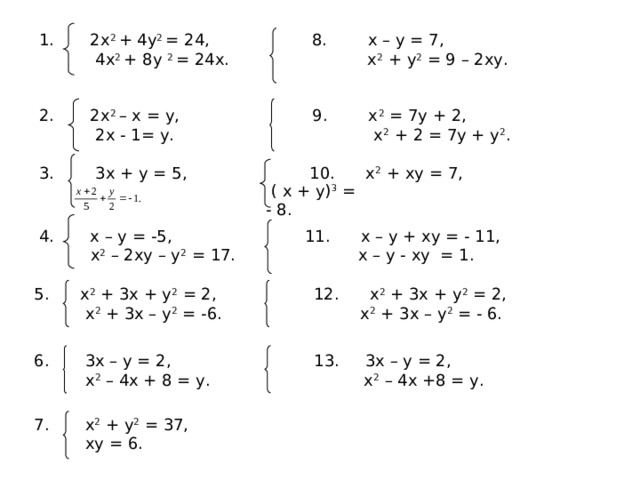
1. 2х 2 + 4у 2 = 24, 8. х – у = 7,

4 x 2 + 8 y 2 = 24 x . х 2 + у 2 = 9 – 2ху.

2. 2 x 2 – x = y , 9. х 2 = 7у + 2,

2 x - 1= y . х 2 + 2 = 7у + у 2 .

3. 3 x + y = 5, 10. х 2 + ху = 7,

( х + у) 3 = - 8.

4. х – у = -5, 11. х – у + ху = - 11,

х 2 – 2ху – у 2 = 17. х – у - ху = 1.

5. х 2 + 3х + у 2 = 2, 12. х 2 + 3х + у 2 = 2,

х 2 + 3х – у 2 = -6. х 2 + 3х – у 2 = - 6.

6. 3х – у = 2, 13. 3х – у = 2,

х 2 – 4х + 8 = у. х 2 – 4х +8 = у.

7. х 2 + у 2 = 37,

ху = 6.