
Теорема Виета
8 класс

Квадратное уравнение общего вида.
Квадратным уравнением
называют уравнение вида
где a, b, c –
действительные числа,
причём а ≠ 0.
a x 2 + b x + c = 0

Приведённое квадратное уравнение.
Квадратное уравнение вида
называется приведённым (а=1).
Квадратное уравнение общего вида можно привести к приведённому:
где

Установим связь между корнями приведенного квадратного уравнения и его коэффициентами.
Уравнение
Корни х 1 и х 2
х 2 – 2х – 3 = 0
х 2 + 5х – 6 = 0
х 2 – х – 12 = 0
х 2 + 7х + 12 =0
х 2 – 8х + 15 =0
х 1 + х 2
х 1 · х 2
х 1 = 3 , х 2 = - 1
2
- 3
- 6
- 5
х 1 = 1 , х 2 = - 6
х 1 = 4 , х 2 = - 3
1
- 12
х 1 = - 4 , х 2 = - 3
- 7
12
х 1 = 5 , х 2 = 3
8
15

Франсуа Виет
(1540 – 1603)
- Француз, жил в конце XVI - начале XVII веков, по профессии юрист, был адвокатом, советником королей Генриха III и IV. Во время войны Франции и Испании раскрыл шифры испанской тайной почты, за что испанская инквизиция приговорила учено--го к сожжению на костре, провозгласив, колдуном и вероотступником. К счастью Генрих IV его не выдал священникам. Математик. Им была сформулирована теория синусов, без доказательства сформулировал всю систему плоской и сферической тригонометрии. “Отец алгебры” - так называют его за введение в эту науку буквенной символики.

Теорема Виета.
Если ч исла х 1 и х 2
являются корнями уравнения
х 2 + р х+ q =0
то справедливы формулы
т.е сумма корней приведённого квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.
Знаменитая теорема, устанавливающая связь коэффициентов
приведенного квадратного уравнения с его корнями , была
обнародована в 1591 г. Теперь она носит имя ВИЕТА.

Обратная теорема

Выберите уравнение сумма корней которого равна – 6, а произведение равно – 11 .
1) х² - 6х + 11 = 0
2) х² + 6х - 11 = 0
з) х² + 6х + 11 = 0
4) х² - 11х - 6 = 0
5) х² + 11х - 6 = 0
х 2 + px + q = 0
x 1 + x 2 = - p
x 1 • x 2 = q

Если х1 = - 5 и х2 = - 1 корни уравнения х² + px + q = 0, то
1) p = - 6 , q = - 5
2) p = 5 , q = 6
з) p = 6 , q = 5
4) p = - 5 , q = - 6
5) p = 5 , q = - 6
х 2 + px + q = 0
x 1 + x 2 = - p
x 1 • x 2 = q

Найдите сумму и произведение корней уравнения х² - 3х – 5 = 0 ( выберите правильный ответ ).
1) х 1 + х 2 = - 3, х 1 • х 2 = - 5
2) х 1 + х 2 = - 5, х 1 • х 2 = - 3
З) х 1 + х 2 = 3, х 1 • х 2 = - 5
4) х 1 + х 2 = 5, х 1 • х 2 = - 3
х 2 + px + q = 0
x 1 + x 2 = - p
x 1 • x 2 = q
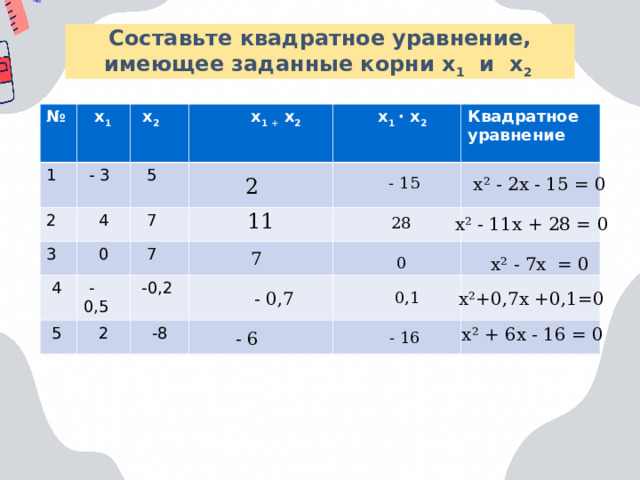
Составьте квадратное уравнение, имеющее заданные корни х 1 и х 2
№
1
х 1
- 3
2
х 2
х 1 + х 2
5
4
3
0
х 1 · х 2
7
4
Квадратное уравнение
7
- 0,5
5
2
-0,2
-8
2
- 15
х² - 2х - 15 = 0
11
28
х² - 11х + 28 = 0
7
0
х² - 7х = 0
- 0,7
0,1
х²+0,7х +0,1=0
х² + 6х - 16 = 0
- 6
- 16

ПРИМЕНЕНИЕ ТЕОРЕМЫ
- Проверяем, правильно ли найдены корни уравнения.
- Определяем знаки корней уравнения не решая его.
- Устно находим корни приведенного квадратного уравнения.
- Составляем квадратное уравнение с заданными корнями.
 0 q q 0 корни разного знака корни одного знака Корней нет p 0 p p p 0 « ─ » у меньшего модуля x 1,2 0 « ─ » у большего x 1,2 0 модуля " width="640"
0 q q 0 корни разного знака корни одного знака Корней нет p 0 p p p 0 « ─ » у меньшего модуля x 1,2 0 « ─ » у большего x 1,2 0 модуля " width="640"
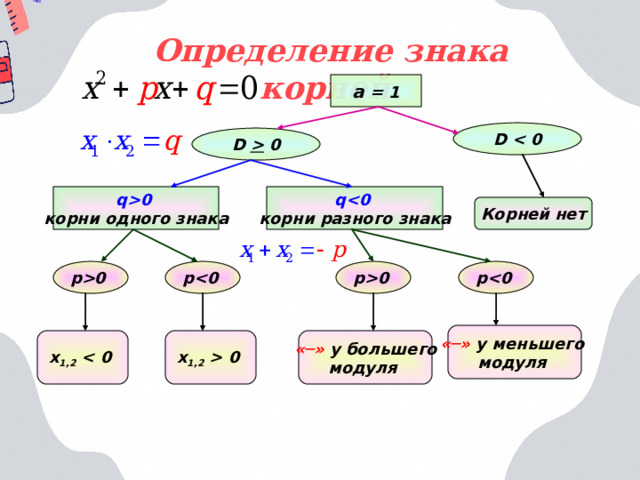
Определение знака корней.
а = 1
D
D 0
q
q 0
корни разного знака
корни одного знака
Корней нет
p 0
p
p
p 0
« ─ » у меньшего
модуля
x 1,2 0
« ─ » у большего
x 1,2 0
модуля

 Получите свидетельство
Получите свидетельство Вход
Вход












 Презентация на тему: "Теорема Виета" (3.02 MB)
Презентация на тему: "Теорема Виета" (3.02 MB)
 0
0 25
25 1
1 Нравится
0
Нравится
0



