Решение прямоугольных треугольников

Доверчивости я пою хвалу,

Но и проверка тоже не обуза…

В определенном месте, на углу

Встречались катет и гипотенуза.

У катета она была одна.

Гипотенузу он любил, не веря сплетням,

Но, в тоже время, на углу соседнем

С другим встречалась катетом она.

И дело все закончилось конфузом-

Вот после этого и верь гипотенузам.

Цель урока:

Совершенствовать навыки решения прямоугольных треугольников, решения прикладных задач;

Не стыдно чего-нибудь не знать,

но стыдно не хотеть учиться.

Сократ

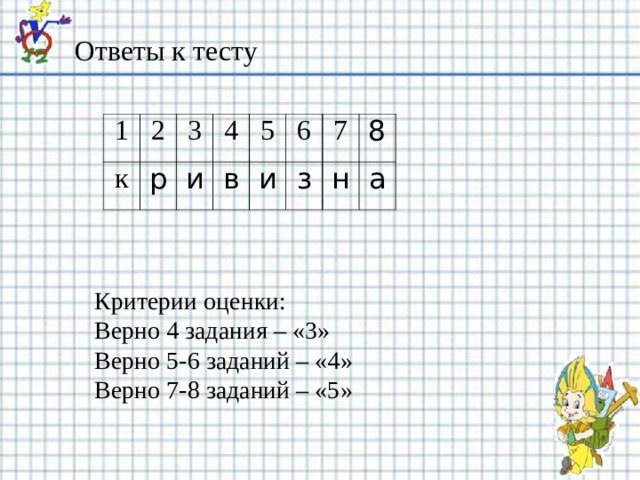
Ответы к тесту

1

к

2

р

3

4

и

в

5

6

и

з

7

8

н

а

Критерии оценки:

Верно 4 задания – «3»

Верно 5-6 заданий – «4»

Верно 7-8 заданий – «5»

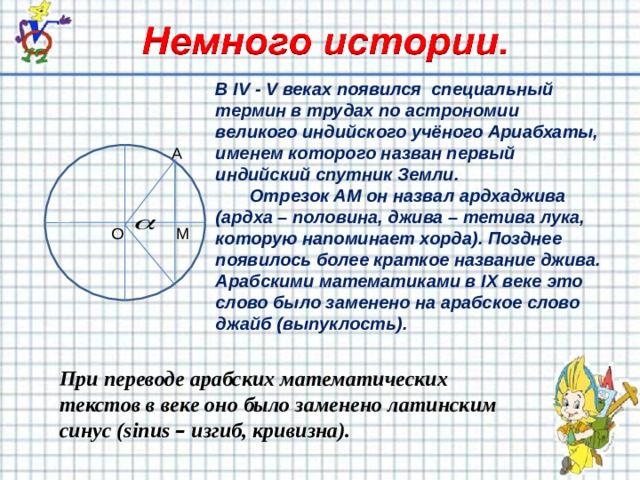
В IV - V веках появился специальный термин в трудах по астрономии великого индийского учёного Ариабхаты, именем которого назван первый индийский спутник Земли.

Отрезок АМ он назвал ардхаджива (ардха – половина, джива – тетива лука, которую напоминает хорда). Позднее появилось более краткое название джива. Арабскими математиками в IX веке это слово было заменено на арабское слово джайб (выпуклость).

А

О

М

При переводе арабских математических текстов в веке оно было заменено латинским синус (sinus – изгиб, кривизна).

Современный синус  , например, изучался как полухорда, на которую опирается центральный угол величиной  , или как хорда удвоенной дуги.

Косинус – это сокращение латинского выражения completely sinus , т. е. “дополнительный синус”

(или “синус дополнительной дуги”; cos  = sin ( 90 ° -  )).

Тангенсы возникли в связи с решением задачи об определении длины тени.

Тангенс (а также котангенс) введен в X веке арабским математиком Абу-ль-Вафой, который

составил и первые таблицы для нахождения

тангенсов и котангенсов.

Название « тангенс » , происходящее от латинского tanger (касаться), появилось в 1583 г.

Tangens переводится как « касающийся » (линия тангенсов – касательная к единичной окружности).

Термин « тригонометрия » означает дословно треугольникомерие или измерения в треугольнике.

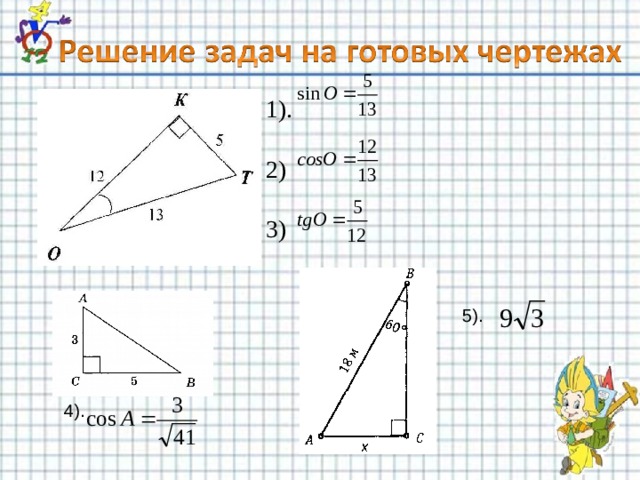
1).

2)

3)

5).

4).

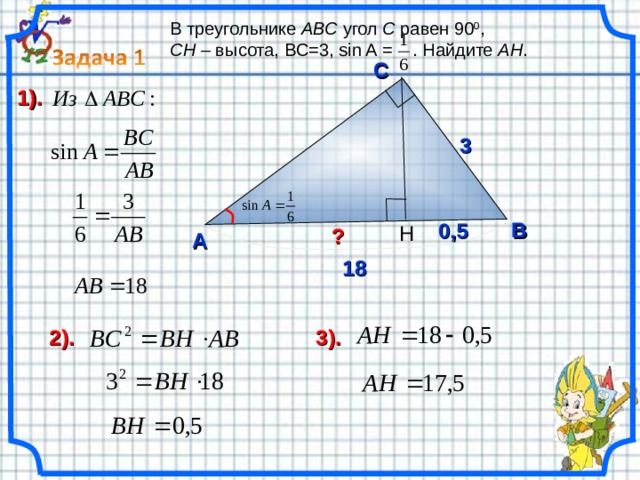
В треугольнике ABC угол C равен 90 0 ,

CH – высота, B С= 3 , sin A = . Найдите АH .

C

1) .

3

B

0,5

H

?

A

18

2 ) .

3 ) .

В параллелограмме АВС D сторона

А D =12 см, а  ВА D = 47 0 30 / .

Найдите площадь параллелограмма,

если его диагональ В D перпендикулярна к стороне АВ.

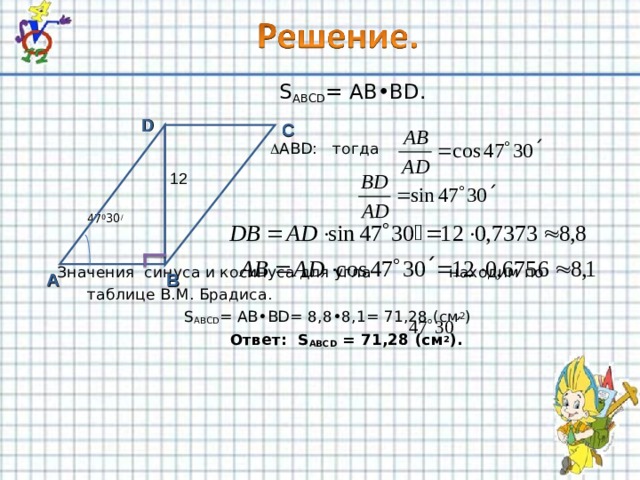
S ABCD = AB•BD.

 ABD: тогда

47 0 30 /

Значения синуса и косинуса для угла находим по

таблице В.М. Брадиса.

S ABCD = AB•BD = 8,8•8,1= 71,28 (см 2 )

Ответ: S ABCD = 71,28 (см 2 ).

D

С

12

В

А

Насыпь шоссейной дороги имеет в верхней части

ширину 60 м. Какова ширина насыпи в нижней части , если угол наклона откосов равен 60 0 , а высота насыпи равна 12 м?

Насыпь шоссейной дороги в разрезе

имеет форму равнобедренной

трапеции ABCD, в которой ВС=60 м,

ВН =12 м,  А =  D = 60 0 .

В  АВН (  Н=90 0 ) :

 АВН=  DCE .

HBCE – прямоугольник НЕ = 60 м.

AD= 2•AH + HE= 60 +

Ответ: 73,86 м.

С

В

D

E

H

А

73, 86 (м).

Критерии отметки :

Количество баллов

Отметка

30-27

Комментарий

26-21

20-15

«4»

Так держать!

«5»

Ещё чуть-чуть

и будет «5»!

«3»

Меньше 15

Будь внимательнее!

Не удовлетворительно

Сделай дома

работу над

ошибками.

Домашняя работа :

Придумать не менее трёх задач по готовым чертежам.

Могу решать задачи самостоятельно

Нужна помощь

Совсем не могу решать задачи

С тригонометрией сейчас

Знакомы даже звери.

Правила все говорят

Четко и уверенно.

И попросим мы зверят

Рассказать их для ребят.

Как мы косинус считаем,

Ты спроси медузу.

— Делим прилежащий катет

На гипотенузу.

• Как мы косинус считаем, Ты спроси медузу. — Делим прилежащий катет На гипотенузу.

Синус вычислить сумеет

Зверь любой из чащи:

На гипотенузу делит

Катет противолежащий.

Чтобы тангенс получить,

Нужно катеты делить.

Вы в числителе берете

Тот, что для угла напротив.

Тот, который прилежит,

В знаменателе пиши.

• Чтобы тангенс получить, Нужно катеты делить. Вы в числителе берете Тот, что для угла напротив. Тот, который прилежит, В знаменателе пиши.

http://im6-tub.yandex.net/i?id=313833065-30-72

http://img1.liveinternet.ru/images/attach/c/2/73/317/73317663_1b8597b9ee0bt.jpg

http://rusforumz.com/library/template/fon/number/67-1.jpg