Решение квадратных уравнений

Разработка урока по теме «Квадратные уравнения» (8 класс).

Тип урока: повторительно-обобщающий.

Цель: повторить и обобщить знания по теме «Квадратные уравнения».

Задачи урока:

* Образовательные:

-систематизировать определения, правила, формулы корней квадратного уравнения;

- рассмотреть различные задания, решаемые с помощью квадратного уравнения;

-проверить умения учащихся решать упражнения по данной теме.

* Развивающие:

- продолжить формирование навыка применения формул корней для решения различных квадратных уравнений;

- развить умение по рациональному использованию формул корней квадратного уравнения;

- привитие интереса учащихся к математике;

- развитие логического мышления.

* Воспитательные:

- повысить чувство ответственности за выполняемую работу;

- воспитание внимания, взаимоуважения и самооценки своего труда.

Оборудование: Интерактивная доска

Ожидаемые результаты.

В результате ученик :

- знает основные понятия и определения данной темы( квадратное уравнение, корень квадратного уравнения, что значит «решить квадратное уравнение»);

- понимает, что квадратное уравнение, как и уравнение в целом может не иметь корней, корнем может быть любое действительное число;

- знает основные формулы корней квадратного уравнения (формула корней квадратного уравнения общего вида, формула четного второго коэффициента, формулы Виета) и умеет их применять;

- осознает, что уравнение является одной из математических моделей явлений реальной действительности;

- знает способы решения биквадратных и дробно- рациональных уравнений.

Ход урока:

1.Мотивационно-ориентировочная часть.

(постановка цели и задач урока, исторические сведения).

Вступительное слово учителя.

Слайд1.

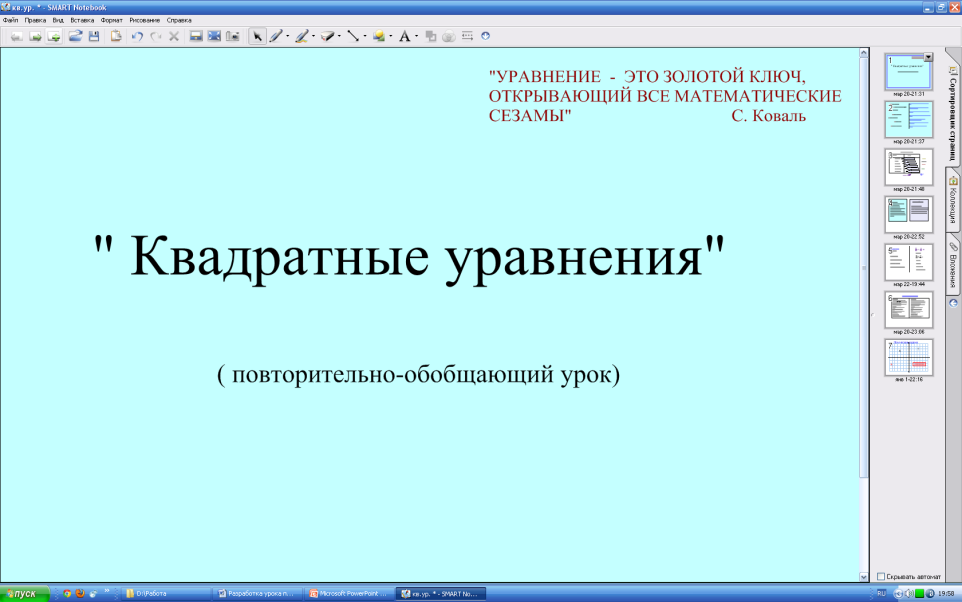
Квадратные уравнения умели решать ещё древние вавилоняне. «Уравнение – это золотой ключ, открывающий все математические сезамы» ( С. Коваль)

Какие ученые математики занимались изучением уравнений, их классификаций, способами решений? (Виет, Фибоначчи) .

Слайд 2.

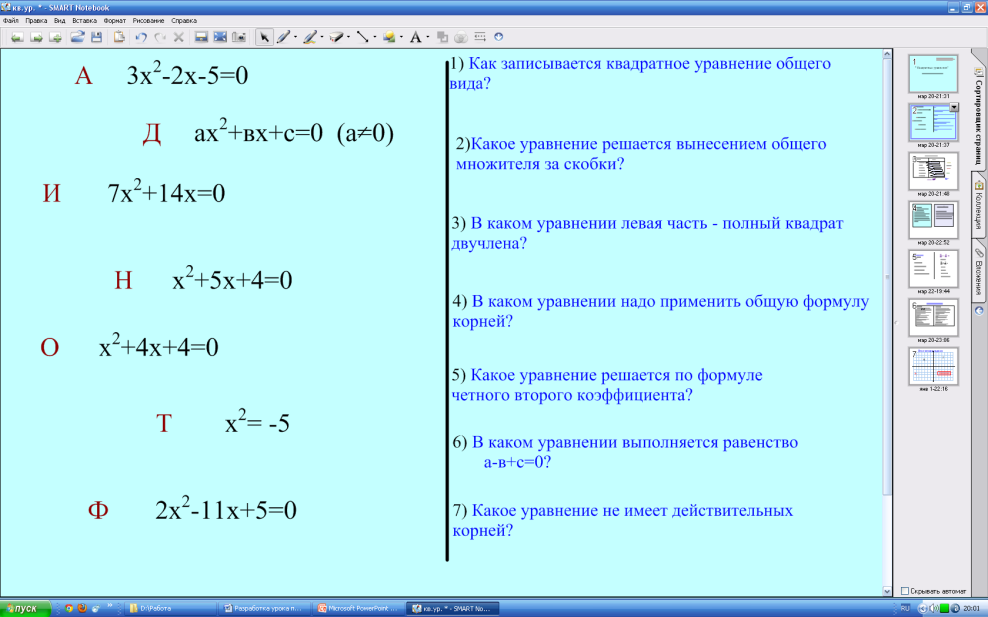
А сейчас мы узнаем имя еще одного математика. Перед вами 7 уравнений одного типа (какого?) Ваша задача – ответить последовательно на вопросы и в тетради отметить букву того уравнения, которое соответствует ответу на вопрос.

Какое получили слово? (Диофант)

Это и есть имя математика из Александрии, жившего в 3 веке нашей эры. Он прожил 84 года, до нас дошли только шесть оригиналов его «Арифметики»,в которых и наблюдается ряд задач, решаемые с помощью квадратных уравнений.

2. Операционно-познавательная часть.

Фронтальная работа с классом. Вопросы:

1. Ученики часто спрашивают: для чего нужно анализировать уравнение – можно сразу начать решение. Что бы вы им ответили?

2. С чего начинается решение квадратного уравнения?

3. От чего зависит количество корней квадратного уравнения?

Слайд 3.

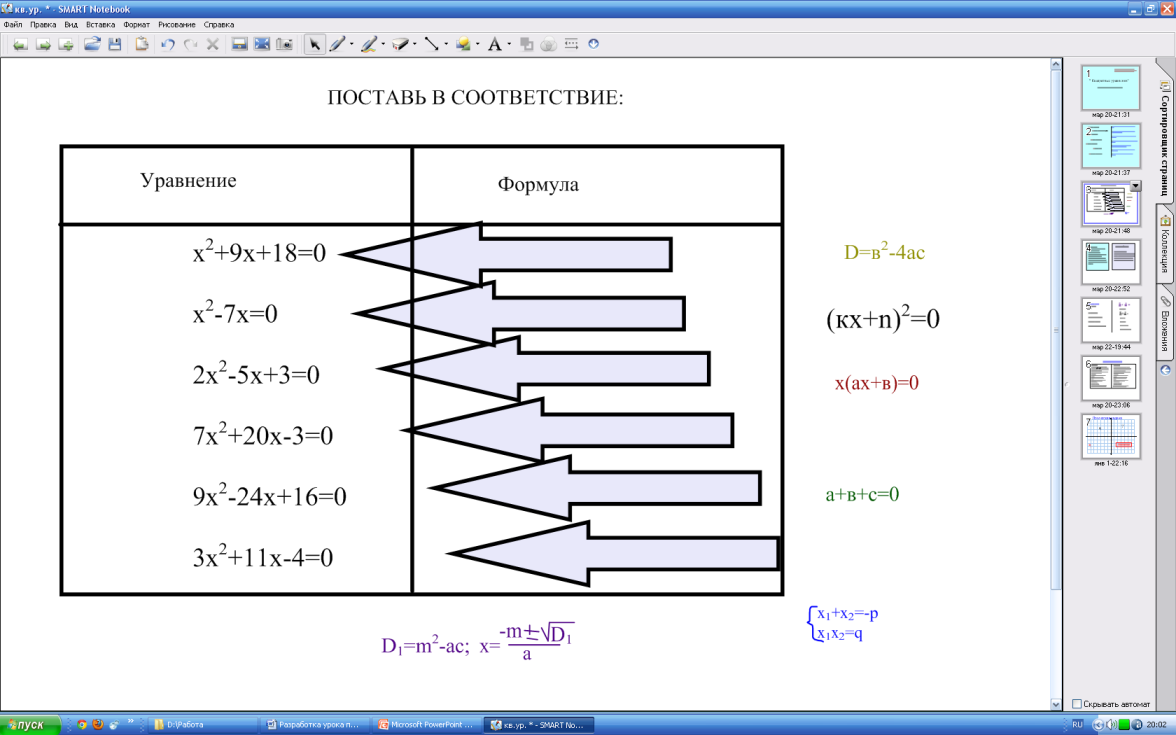
Определив, что уравнение имеет корни, анализируя коэффициенты, вы выбираете формулу корней квадратного уравнения. Итак, сейчас вам предстоит (обсуждая ответ с соседом по парте) определить соответствие формулы квадратному уравнению.

(проверяем результат: 1 ученик работает на интерактивной доске, двигая формулы к соответствующему уравнению)

Два последних уравнения решаются на доске и в тетрадях.

Слайд 4.

Знания решений квадратных уравнений применяются при решении других уравнений и задач. К доске приглашаются 2 ученика для работы по карточке 1 и карточке 2.

В это время фронтальная работа с классом:

1. Какие уравнения сводятся к решению квадратного? (биквадратные и дробно- рациональные)

2. Вспомните определение биквадратного уравнения и алгоритм его решения.

Слайд 5.

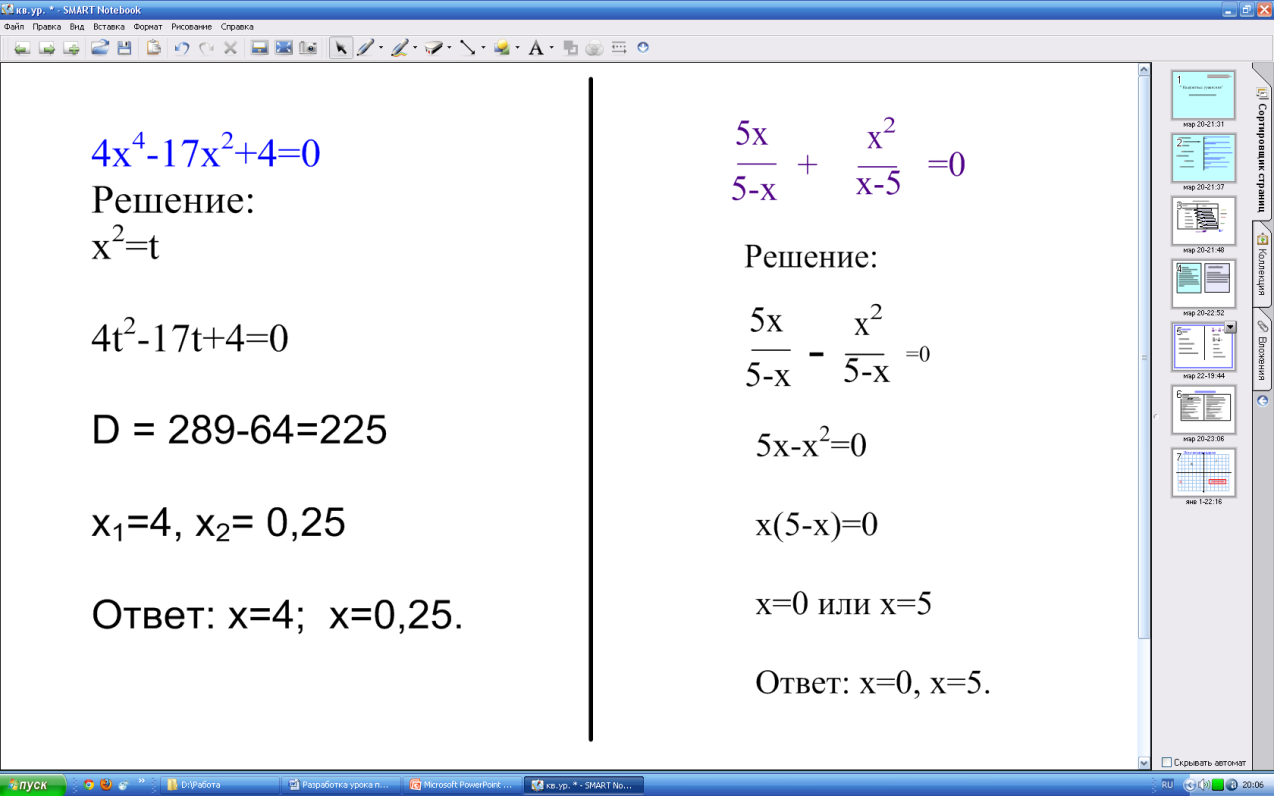
Перед вами решение биквадратного и дробно- рационального уравнения:

1. Согласны ли вы с решением биквадратного уравнения?

2. Найти ошибку в решении дробно-рационального уравнения.

Проверяется и обсуждается работа по карточке1 и карточке 2.

( используется команда «отодвинь и ты узнаешь решение»).

3. Рефлексивно- оценочная часть.

Самостоятельная работа(тестирование), взаимопроверка.(ключевое слово «ДЦ Лазурный).

Слайд 6.

Дополнительная логическая задача:

Слайд 7.

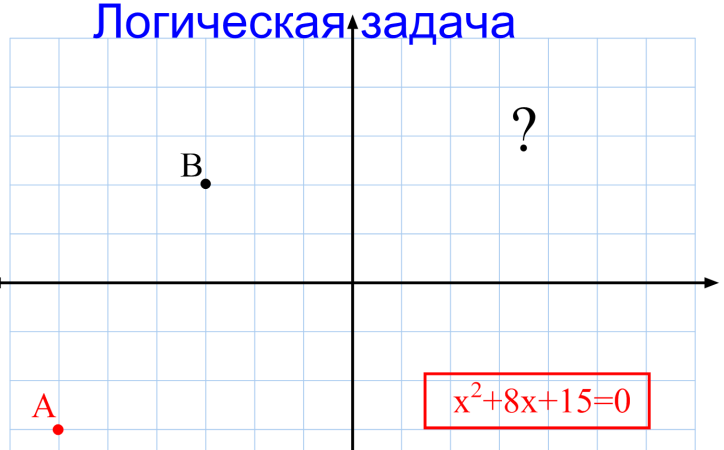
Подведение итога урока, выставление оценок.