Решение систем уравнений с двумя переменными

Презентация  предназначена для закрепления темы "Решение систем уравнений в 9 классе" Это 3 или 4 урок в теме.На первых слайдах решается кроссворд, позволяющий сформулировать тему урока, Затем вспоминаются графики элементарных функций и их формулы .Сообщается, что есть еще более сложные графики, которые изучаются в высшей математике, показываются некоторые из них. После идет проверка домашнего задания и выставляются баллы в лист самоконтроля.

На одном примере напоминается с подробным разбором как решаются системы уравнений. Далее следует групповая работа с последующей самопроверкой и выставлением баллов в лист самоконтроля. После дети пишут тест, состоящий из 3 заданий обязательной части и 1 задания второй степени сложности. Завершается работа над листом самоконтроля, который сдается на проверку. Дается домашнее задание. Урок насыщен новой для ребят информацией,рассматриваются раличные виды даботы. У ребят есть возможность выбора,что позволяет работать каждому.Работа в группе дает возможность выслушать мнение товарищей и аргументировать их и свои выводы.

Графический способ решения нелинейных систем уравнений

Учитель математики

МАОУ «СОШ №10» г. Пермь

Решите кроссворд:

4

2

Г

3

1

П

А

И

В

А

5

П

Р

Н

О

Р

6

А

Е

С

К

Ч

И

Ф

Р

Г

Й

И

К

И

А

Е

Г

Р

Р

З

У

Б

У

Б

М

О

Ж

Л

О

Е

Н

Н

А

Л

О

А

Т

С

Т

Ь

2. График квадратичной функции.

1.Независимая переменная.

4. График обратной пропорциональности.

3. Направление ветвей параболы при а

5 . График уравнения: х 2 +у 2 = R .

6. Способ решения систем уравнений .

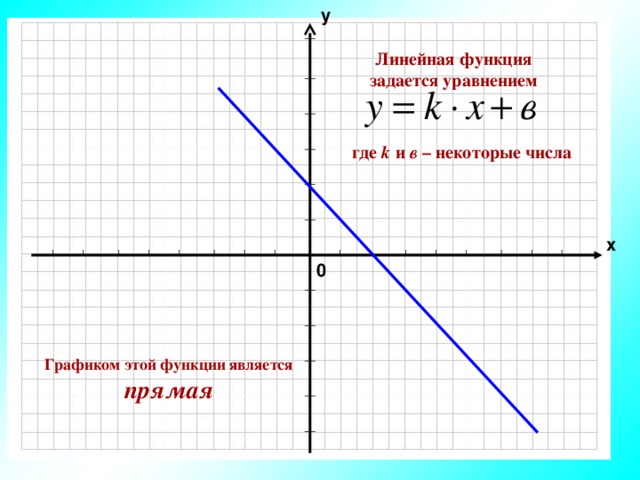
у

Линейная функция задается уравнением

где k и в – некоторые числа

х

0

Графиком этой функции является прямая

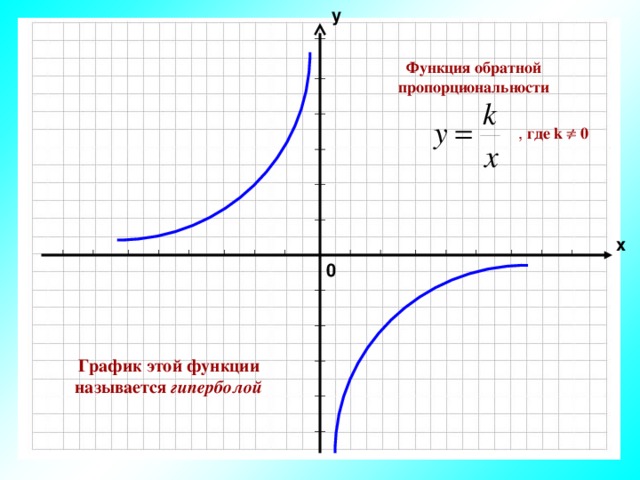
у

Функция обратной пропорциональности

, где k  0

х

0

График этой функции называется гиперболой

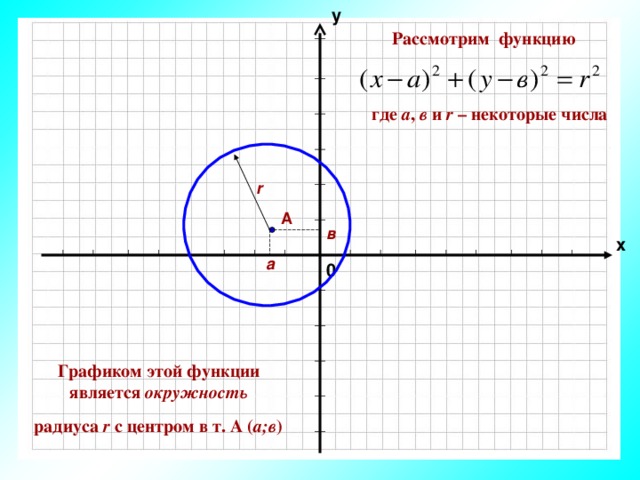
у

Рассмотрим функцию

где а , в и r – некоторые числа

r

А

в

х

а

0

Графиком этой функции является окружность

радиуса r с центром в т. А ( а;в )

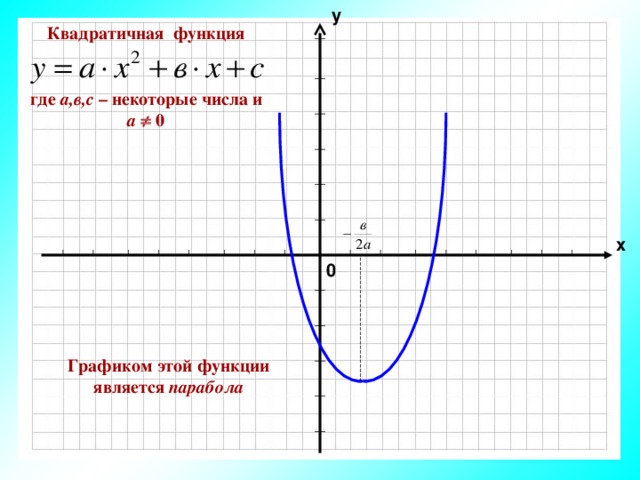
у

Квадратичная функция

где а,в,с – некоторые числа и а  0

х

0

Графиком этой функции является парабола

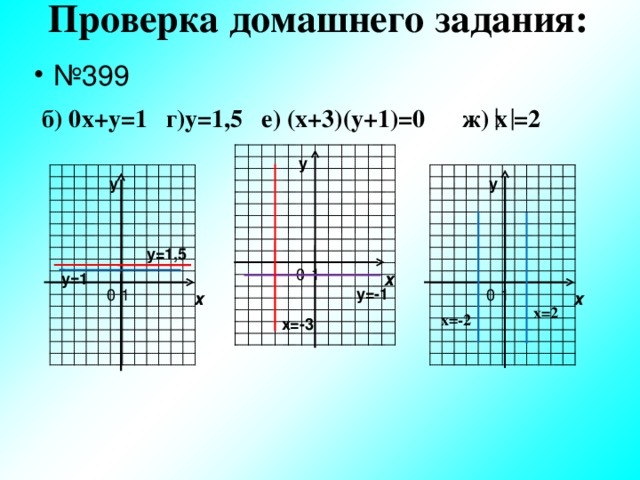
Проверка домашнего задания:

• № 399

б) 0х+у=1 г)у=1,5 е) (х+3)(у+1)=0 ж) х =2

у

у

у

у=1,5

х

у=1

у=-1

х

х

x=2

x=-2

х=-3

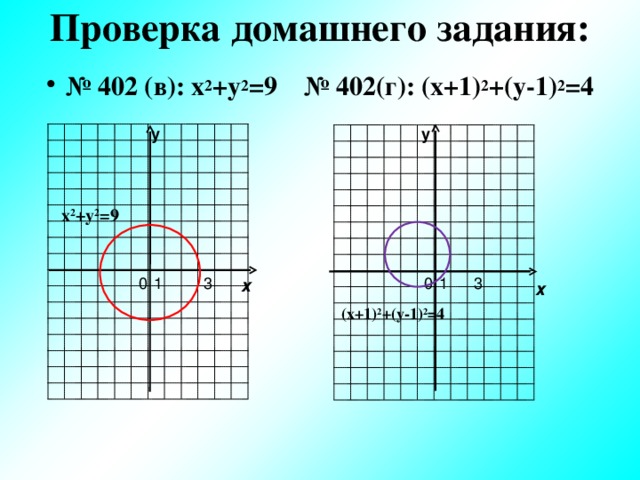
Проверка домашнего задания:

• № 402 (в): х 2 +у 2 =9 № 402(г): (х+1) 2 +(у-1) 2 =4

у

у

х 2 +у 2 =9

х

х

(х+1) 2 +(у-1) 2 =4

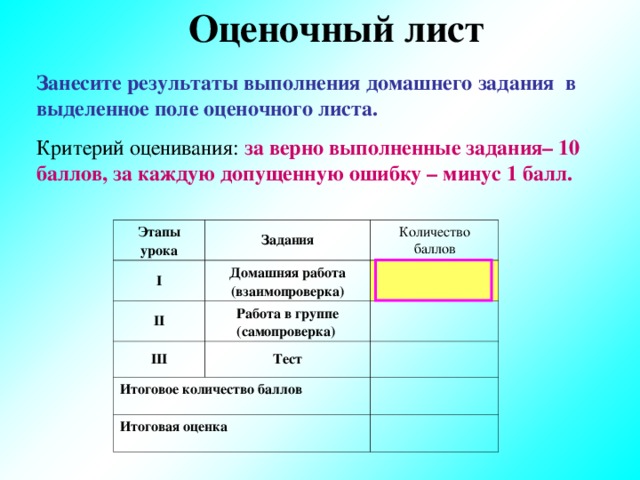
Оценочный лист

Занесите результаты выполнения домашнего задания в выделенное поле оценочного листа.

Критерий оценивания: за верно выполненные задания– 10 баллов, за каждую допущенную ошибку – минус 1 балл.

Этапы урока

I

Задания

Количество баллов

Домашняя работа (взаимопроверка)

II

III

Работа в группе (самопроверка)

Итоговое количество баллов

Тест

Итоговая оценка

Графиком уравнения с двумя переменными называется, как вы знаете, множество точек координатной плоскости, координаты которых обращают уравнение в верное равенство.

Причем иногда уравнения могут быть достаточно сложными, а графики таких уравнений – очень необычными по форме.

Давайте рассмотрим несколько примеров таких уравнений, используемых в высшей математике.

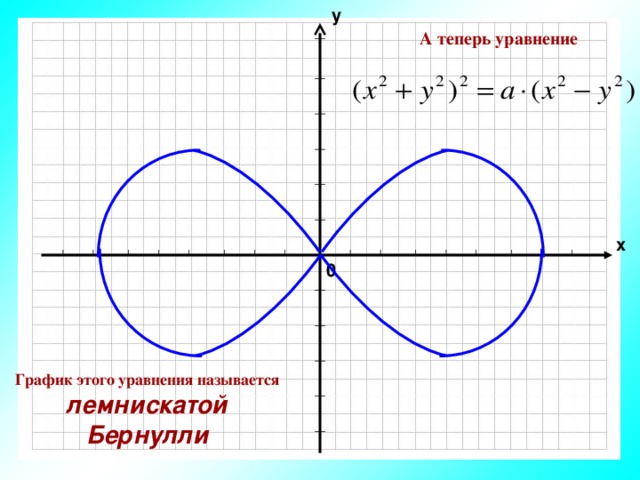
у

А теперь уравнение

х

0

График этого уравнения называется лемнискатой Бернулли

у

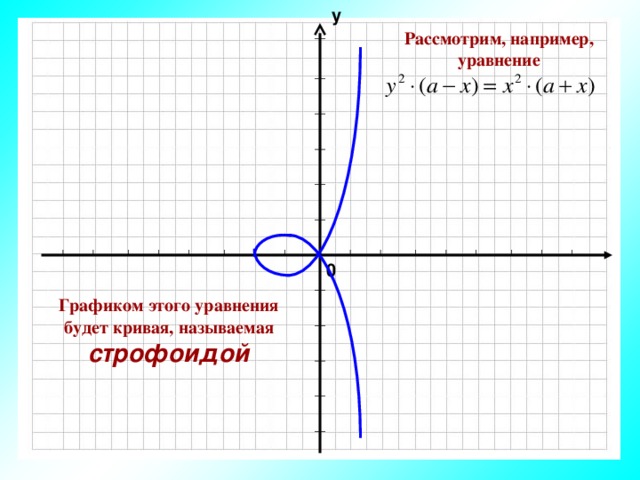
Рассмотрим, например, уравнение

0

Графиком этого уравнения будет кривая, называемая строфоидой

у

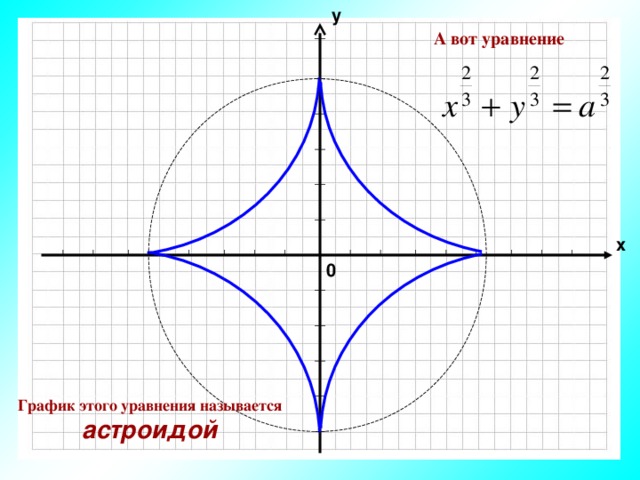
А вот уравнение

х

0

График этого уравнения называется астроидой

у

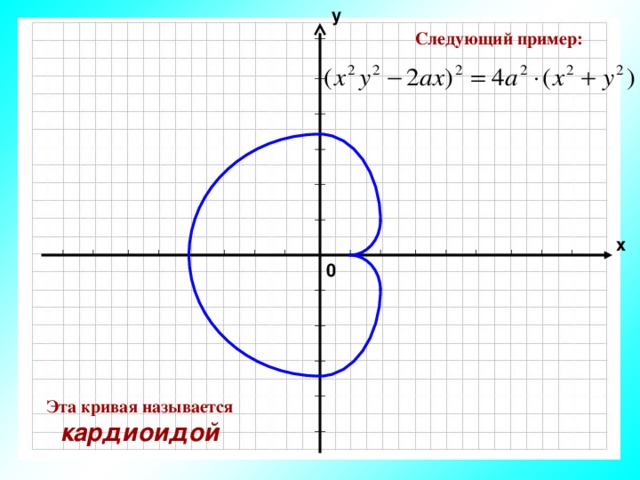
Следующий пример:

х

0

Эта кривая называется кардиоидой

Конечно, Вам придется иметь дело с уравнениями попроще, и, тем не менее, графики их нужно уметь строить.

!

А теперь к делу – учимся решать системы уравнений с двумя переменными графически!

!

?

Уравнение 1,

Уравнение 2;

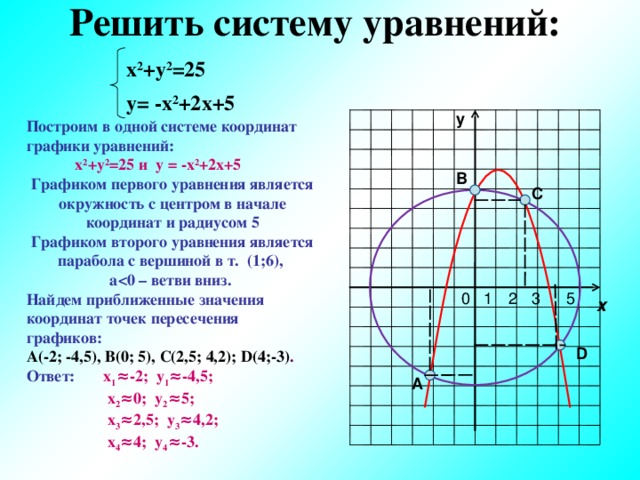
Решить систему уравнений:

х 2 +у 2 =25

у= -х 2 +2х+5

у

Построим в одной системе координат графики уравнений:

х 2 +у 2 =25 и у = -х 2 +2х+5

Графиком первого уравнения является окружность с центром в начале координат и радиусом 5

Графиком второго уравнения является парабола с вершиной в т. (1;6),

а ветви вниз.

Найдем приближенные значения координат точек пересечения графиков:

А(-2; -4,5), В(0; 5), С(2,5; 4,2); D (4;-3) .

Ответ: х 1 ≈-2; у 1 ≈-4,5;

х 2 ≈0; у 2 ≈5;

х 3 ≈2,5; у 3 ≈4,2;

х 4 ≈4; у 4 ≈-3.

В

С

х

D

А

Задания для групповой работы :

• Группа №1: Решите графически систему уравнений:

Группа №2: Решите графически систему уравнений:

• Группа №3: Решите графически систему уравнений:

• Дополнительно: №525

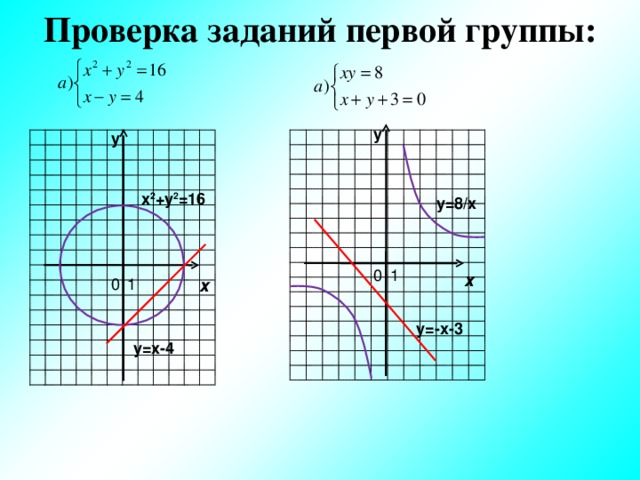
Проверка заданий первой группы:

у

у

х 2 +у 2 =16

y=8/x

х

х

y=-x-3

у=х-4

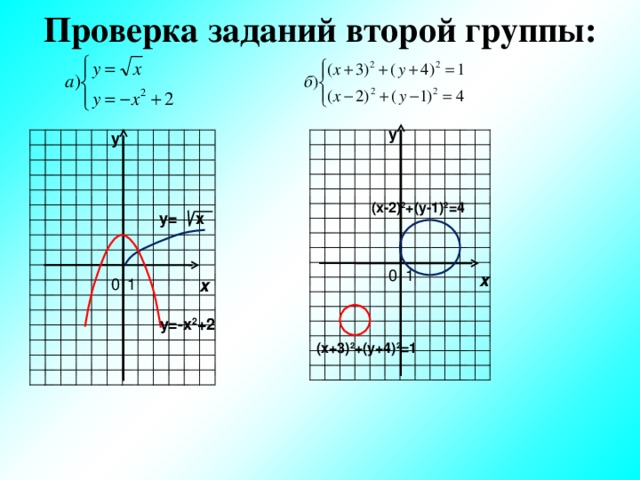
Проверка заданий второй группы:

у

у

(х-2) 2 +(у-1) 2 =4

у= х

х

х

у=-х 2 +2

(х+3) 2 +(у+4) 2 =1

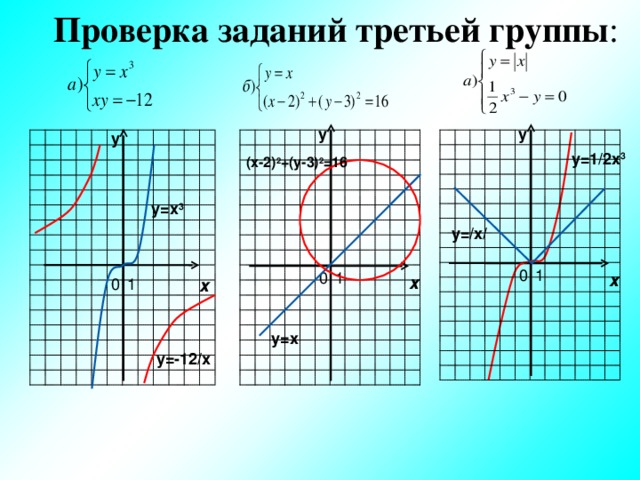
Проверка заданий третьей группы :

у

у

у

у=1/2х 3

(х-2) 2 +(у-3) 2 =16

у=х 3

у=/х/

х

х

х

у=х

y= -12 /x

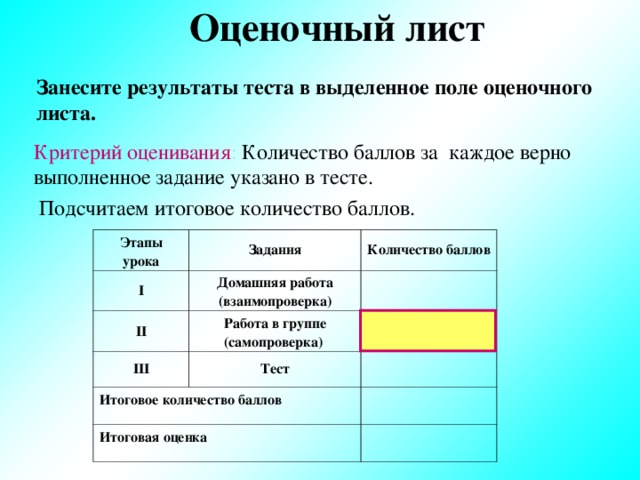
Оценочный лист

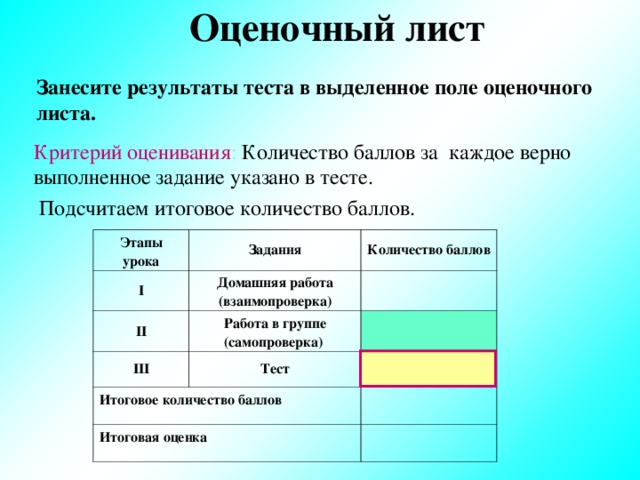
Занесите результаты теста в выделенное поле оценочного листа.

Критерий оценивания : Количество баллов за каждое верно выполненное задание указано в тесте.

Подсчитаем итоговое количество баллов.

Этапы урока

I

Задания

Количество баллов

Домашняя работа (взаимопроверка)

II

III

Работа в группе (самопроверка)

Итоговое количество баллов

Тест

Итоговая оценка

Тестовая работа

Вариант I Часть I

1.  (1 балл) Найти корни неполного квадратного уравнения 2х 2 +5х=0:

а) 0;-2,5; б) 2;5 ; в) 0; -0,4;

г) корней нет.

Тестовая работа

Вариант II Часть I

1.  (1 балл) Найти корни неполного квадратного уравнения 2х 2 - 18=0:

а) 2;18; б) 3;0 ; в) 3;-3;

г) корней нет.

2.  (1 балл) Укажите координаты центра окружности и радиус: х 2 +(у-5) 2 =9 .

Ответ ___ ______

3.  (1 балл) Сколько решений имеет система уравнений , изображенная на графике:

2.  (1 балл) Укажите координаты центра окружности и радиус: (х+3) 2 +у 2 =49 .

Ответ _______

3.  (1 балл) Сколько решений имеет система уравнений , изображенная на графике:

а) одно; б) два ; в) три; г) нет решений.

Часть II

4.  (2 балла) С помощью графиков определите, сколько решений имеет система уравнений:

Ответ____________

а) одно; б) два ; в) три; г) нет решений.

Часть II

4.  (2 балла) С помощью графиков определите, сколько решений имеет система уравнений:

Ответ________

Тестовая работа

Вариант I Часть I

1.  (1 балл) Найти корни неполного квадратного уравнения 2х 2 +5х=0:

а) 0;-2,5; б) 2;5 ; в) 0; -0,4;

г) корней нет.

Тестовая работа

Вариант II Часть I

1.  (1 балл) Найти корни неполного квадратного уравнения 2х 2 - 18=0:

а) 2;18; б) 3;0 ; в) 3;-3;

г) корней нет.

2.  (1 балл) Укажите координаты центра окружности и радиус: х 2 +(у-5) 2 =9 .

Ответ __ ( 0, -5) _R = 3 ______

3.  (1 балл) Сколько решений имеет система уравнений , изображенная на графике:

2.  (1 балл) Укажите координаты центра окружности и радиус: (х+3) 2 +у 2 =49 .

Ответ _(-3, 0)__ R =_7___

3.  (1 балл) Сколько решений имеет система уравнений , изображенная на графике:

а) одно; б) два ; в) три ; г) нет решений.

Часть II

4.  (2 балла) С помощью графиков определите, сколько решений имеет система уравнений:

Ответ __( три)__________

а) одно; б) два ; в) три; г) нет решений.

Часть II

4.  (2 балла) С помощью графиков определите, сколько решений имеет система уравнений:

Ответ _три

ответы

Оценочный лист

Занесите результаты теста в выделенное поле оценочного листа.

Критерий оценивания : Количество баллов за каждое верно выполненное задание указано в тесте.

Подсчитаем итоговое количество баллов.

Этапы урока

I

Задания

Количество баллов

Домашняя работа (взаимопроверка)

II

III

Работа в группе (самопроверка)

Итоговое количество баллов

Тест

Итоговая оценка

Домашнее задание:

• № 417, № 523 (а, г, е)

Д о п о л н и т е л ь н о :

№ 526.