| | Шиянова Татьяна Алексеевна, учитель математики МБОУ СОШ № 11 им. Г.С. Титова Щелковского МР МО |
|
|
|
МЕТОДИКА ОБУЧЕНИЯ
РЕШЕНИЮ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
ПРИ ПОДГОТОВКЕ
К ГОСУДАРСТВЕННОЙ ИТОГОВОЙ АТТЕСТАЦИИ
ПО МАТЕМАТИКЕ В 9-М КЛАССЕ В НОВОЙ ФОРМЕ
|
| Оглавление
|
|
-
| Введение | 2 |
-
| Общие рекомендации при организации работы по подготовке к ГИА-9 в новой форме | 3 |
-
| Методика обучения решению систем линейных уравнений | 5 |
-
| Заключение | 16 |
-
| Список литературы | 17 |
1. ВВЕДЕНИЕ
Введение государственной итоговой аттестации по математике в новой форме (ГИА) в 9 классе вызывает необходимость изменения в методах и формах работы учителя.
Эта необходимость обусловлена тем, что изменились требования к знаниям, умениям и навыкам учащихся в материалах экзамена по математике. Само содержание образования существенно не изменилось, но существенно сместился акцент к требованиям умений и навыков. Изменилась формулировка вопросов: вопросы стали нестандартными, задаются в косвенной форме, ответ на вопрос требует детального анализа задачи. И это всё в первой части экзамена, которая предусматривает обязательный уровень знаний. Содержание задач изобилует математическими тонкостями, на отработку которых в общеобразовательной программе не отводится достаточное количество часов. В обязательную часть включаются задачи, которые либо изучались давно, либо на их изучение отводилось малое количество времени (проценты, стандартный вид числа, свойства числовых неравенств, задачи по статистике, чтение графиков функций), а также задачи, требующие знаний по другим предметам, например, по физике. Кроме этого в общеобразовательных классах, как правило, уровень подготовки учащихся различный. И если для одних учащихся важно научиться решать задания I части, так как это обеспечивает получение удовлетворительной отметки на экзамене, то для других учащихся нужно и важно научиться решать более сложные задания.
2. ОБЩИЕ РЕКОМЕНДАЦИИ ПРИ ОРГАНИЗАЦИИ РАБОТЫ
ПО ПОДГОТОВКЕ К ГИА-9 В НОВОЙ ФОРМЕ
Можно предложить следующую систему работы по подготовке к ГИА по математике в 9 классе:
1. Изменить тематическое планирование таким образом, чтобы осталось достаточное количество часов на повторение всего учебного материала. Часы можно сэкономить на тех темах, которые не требуют выработки навыков, а проходят в плане ознакомления, а также сократить число часов на отработку навыков невостребованных тем. Это надо делать очень осторожно, тщательно проанализировав содержание экзаменационных работ.
2. Включать в изучение текущего учебного материала задания, соответствующие экзаменационным заданиям, начиная с первого изучения темы (например, тема «Системы линейных уравнений с двумя переменными» начинает изучаться в 7-ом классе).
3. В содержание текущего контроля включать экзаменационные задачи, как I, так и II части. При этом нужно, чтобы учащиеся при выполнении тестовых заданий не только писали ответы, но и в обязательном порядке записывали решение (там, где это необходимо). Это нужно, чтобы, во-первых, учитель видел причину допущения ошибок, а, во-вторых, для исключения массового списывания.
4. При организации итогового повторения для менее подготовленных учащихся продолжать отрабатывать умения и навыки, требующиеся для получения положительной отметки на экзамене, а с более подготовленными учащимися решать, в том числе и задания второй части.
5. Уроки итогового повторения строятся следующим образом. На уроке разбираются типовые задачи по 2-3 темам. На дом задаются аналогичные задачи. На следующем уроке выясняются затруднения, которые возникли у учеников, прорабатываются эти задачи. Затем даётся проверочная работа.
Подготовку ко второй части работы можно осуществлять как на уроках, так и во внеурочное время на элективных курсах. Для этого желательно использовать сборники для подготовки к экзаменам, рекомендованные ФИПИ и МИИО. Важным условием успешной подготовки к экзаменам является тщательность в отслеживании результатов учеников по всем темам и в своевременной коррекции уровня усвоения учебного материала.
3. МЕТОДИКА ОБУЧЕНИЯ РЕШЕНИЮ
СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
В 7-ом классе при изучении темы «Системы двух линейных уравнений с двумя переменными» мы знакомим учащихся с тремя способами решения систем уравнений: способом подстановки, способом сложения и графическим способом.
Решение систем линейных уравнений с двумя переменными x и y способом подстановки состоит в следующем:
Выразить одну переменную через другую в одном из уравнений;
подставить найденное выражение вместо переменной в другое уравнение;
решить полученное уравнение с одной переменной;
подставить найденный корень в выражение (п.1);
в ответе записать полученную пару (x0, y0).
Решение систем двух линейных уравнений с двумя переменными x и y способом алгебраического сложения состоит в следующем:
Умножением обеих частей одного уравнения или двух уравнений привести их к виду, когда коэффициенты при одной из переменных являются противоположными числами;
Записать систему, в которой одно уравнение получено сложением левых и правых частей полученных уравнений (полученное уравнение содержит только одну переменную), в качестве второго записать одно из уравнений данной системы;
Решить уравнение с одной переменной;
Подставить найденный корень во второе уравнение и найти его корень;
В ответе записать пару (x0, y0), где x0 и y0 – корни уравнений, найденные в пп. 3 и 4.
1. Решите систему уравнений 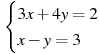 .
.
Решение (способ подстановки):
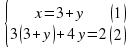
Решим уравнение 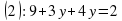
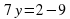
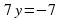
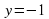
Подставим y= -1 в (1) уравнение системы
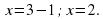
Ответ: (2; -1).
2. Решите систему уравнений 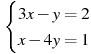 .
.
Решение (способ сложения):
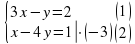
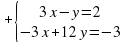
_________________
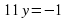
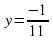
Подставим 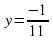 во (2) уравнение системы:
во (2) уравнение системы:
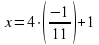
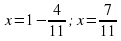
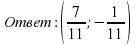
Отработку решения систем линейных уравнений можно осуществлять на заданиях, аналогичных заданиям из банка данных ГИА (прототип № 16), таких как задания № 3-6.
В заданиях № 3-4 появляется один дополнительный шаг: учащиеся должны сами составить систему уравнений, а затем ее решить.
3. Вычислите координаты точки пересечения прямых 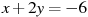 и
и 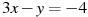 .
.
Решение:
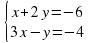
Решим способом подстановки.
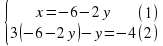
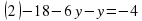
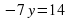
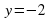
Подставим 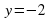 в уравнение (1):
в уравнение (1):
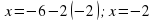
Ответ: (-2; -2).
4. Вычислите координаты точки пересечения прямых  и
и  .
.
Решение:
____________________

Подставляем  в уравнение (2):
в уравнение (2):
Ответ: 
В заданиях № 5-6 учащиеся должны вспомнить определение линейного уравнения, а лучше линейной функции y=kx+b, и составить два уравнения (систему уравнений) учитывая, что точки принадлежат данной прямой. Затем нужно решить эту систему уравнений относительно k и b и записать уравнение прямой, подставив полученные значения k и b в уравнение y=kx+b.
5. На координатной плоскости отмечены точки C и D. Какое уравнение задает прямую, проходящую через эти точки?
Решение:
Уравнение прямой y=kx+b.
Учитывая, что точки D (19;15) и C (14; 10) принадлежат прямой y=kx+b, получаем систему уравнений:
____________________


Найдем b из уравнения (2):

Запишем уравнение прямой: y = x - 4.
Ответ: y = x - 4.
6. На координатной плоскости проведена прямая CD. Укажите уравнение этой прямой.

Варианты ответа
Решение:
Решение этого задания точно такое же, как и задания № 5. Отличие состоит в том, что здесь нужно выбрать правильный вариант ответа, а в задании № 5 записать полученное уравнение прямой.
В задании № 5 получили уравнение y = x - 4. Запишем его по-другому: x - y = 4.
Выберем ответ № 3.
7. В какой координатной четверти находится точка пересечения прямых и
и  ?
?
Варианты ответа
| 1. | В I четверти |
| 2. | В II четверти |
| 3. | В III четверти |
| 4. | В IV четверти |
|
Решение:
При решении этого задания нужно составить систему
Решив ее, получим, что x = -2; y = 1, т.е. получим точку с координатами (-2; 1), которая лежит во II четверти. Это же задание можно выполнить графически.
Кстати, при решении систем двух линейных уравнений можно в качестве дополнительного вопроса спрашивать у учащихся, какой координатной четверти принадлежит точка с координатами (х; у).
8. Каким уравнением задается прямая, проходящая через точки A и B
и B ?
?
Варианты ответа
Решение:
Это задание решается аналогично заданиям № 5 и 6.
При отработке навыков решения систем линейных уравнений в 7-ом классе это задание и задание типа № 6 следует решать, составляя систему уравнений. А уже при изучении темы «Системы уравнений второй степени с двумя переменными» в 9-ом классе можно показать более простой способ решения: нужно просто подставить координаты точек А и В в уравнения, данные в ответе, и выбрать то уравнение, корнями которого являются координаты обеих точек. В данном случае это уравнение № 3.
9. Решите систему уравнений  с помощью графика
с помощью графика
Решение:
Решением является точка пересечения прямых.
Ответ: (2; 0).
Заданий второй части по теме «Системы двух линейных уравнений с двумя переменными» практически нет. В качестве примеров можно разобрать задания № 10 – 12 из сборника заданий для подготовки к государственной итоговой аттестации в 9-ом классе (см. список литературы с. 18 (1)).
10. Решить систему уравнений
Решение:
___________________


Подставим x=1 в уравнение (2)

Ответ: (1; -3).
11. Решить систему уравнений
Решение: Решим систему способом подстановки
Подставим x=-7y в уравнение (2)

x=-3.
Ответ: (- 3; 1).
12. Найти решения уравнения
Решение:
Сумма квадратов двух выражений равна нулю тогда и только тогда, когда каждое из выражений равно 0.
Т.е. решение данного уравнения сводится к решению системы уравнений:

_________________


Подставим  в (1) уравнение системы
в (1) уравнение системы
Ответ: 
ЗАКЛЮЧЕНИЕ
Решение всех рассмотренных заданий нужно по возможности разобрать и отработать их решение, как было уже сказано выше, в 7-ом классе. В 9-ом классе при работе над темой «Системы уравнений второй степени с двумя переменными» продолжить эту работу, решая аналогичные задания только уже для систем уравнений второго порядка. А при организации итогового повторения для менее подготовленных учащихся продолжать отрабатывать умения и навыки, требующиеся для получения положительной отметки на экзамене, а с более подготовленными учащимися решать, в том числе и задания второй части.
СПИСОК ЛИТЕРАТУРЫ
1. Алгебра: сб. заданий для подготовки к гос. итоговой аттестации в 9 кл./ [Л. В. Кузнецова, С. Б. Суворова, Е. А. Бунимович и др.]. – 5-е изд. -– М.: Просвещение, 2010. – 239с. : ил. – (Государственная итоговая аттестация).
2. Алгебра. 7 класс. Тематические тесты. Промежуточная аттестация / Под редакцией Ф.Ф. Лысенко, С.Ю. Кулабухова. – Ростов-на-Дону: Легион-М, 2011. – 173 с. – (Тематические тесты).
3. ГИА по математике. 9 класс : учебное пособие / Л.О. Денищева [ и др.]. – М. : учебное пособие БИНОМ. Лаборатория знаний, 2011. – 264 с. : ил. – (Готовимся к итоговой аттестации).
4. Открытый банк заданий по математике ГИА. http://mathgia.ru:8080/or/gia12/Main.html?view=Pos

 Получите свидетельство
Получите свидетельство Вход
Вход



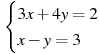 .
.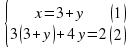
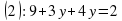
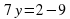
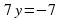
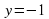
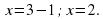
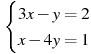 .
.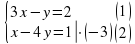
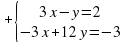
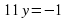
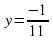
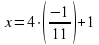
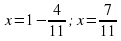
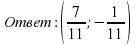
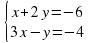
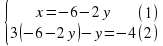
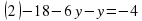
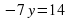
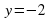
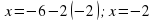









 Методика обучения решению систем линейных уравнений при подготовке к ГИА по математике в новой форме (0.1 MB)
Методика обучения решению систем линейных уравнений при подготовке к ГИА по математике в новой форме (0.1 MB)
 0
0 1709
1709 132
132 Нравится
0
Нравится
0


