Степанова Р.А., учитель информатики МБОУ «Кюсюрская СОШ»
Тема урока: «Основы логики».
Цели урока:
систематизация и обобщение знаний учащихся по основам логоки;
формирование навыков решения заданий ЕГЭ по информатике с использованием элементов алгебры логики.
Задачи урока:
Образовательная – закрепление теоретических знаний учащихся по логическим операциям и законам, практическое их применение для решения задач, составления таблиц истинности, преобразования логических выражений.
Развивающая – совершенствование внимания, логического и алгоритмического мышления учащихся;
Воспитательные – формирование у учащихся методологического подхода к познавательной и практической деятельности, настойчивости и инициативности в преодолении трудностей.
Тип урока: Урок закрепления знаний.
Учащиеся: 11 класс.
Учебная деятельность учащихся: индивидуальная, групповая.
Оборудование: компьютер, проектор, интерактивная доска.
Программное обеспечение: Microsoft Office Power Point;
Презентация «Основные понятия логики»
План урока:
Организационный момент, мотивация – 1 минута;
Актуализация опорных знаний – 6 минут;
Решение задач на основе изученного материала – 20 минут;
Выполнение практической работы – 10 минут;
Постановка домашнего задания – 2 минуты;
Подведение итогов урока – 1 минута;
Ход урока
Организационный момент, мотивация.
На сегодняшнем уроке мы завершаем тему “Основы логики”. Алгебра логики изучает строение сложных логических высказываний и способы установления их истинности с помощью алгебраических методов.
Наша задача – научиться применять основные логические операции, логические законы, законы преобразования для решения задач. ЕГЭ по информатике включает несколько типов логических задач, решение некоторые из них сегодня рассмотрим на уроке.
Актуализация опорных знаний и их коррекция.
Для успешного выполнения заданий по основам логики необходимо
знать и помнить основные логические операции, их обозначения и таблицы истинности.
Какие логические операции вы знаете?
Давайте подробно вспомним их.
(Показ слайдов: «Отрицание», «Конъюнкция», «Дизъюнкция», «Импликация»)
Решение задач на основе повторение изученного материала.
Решим задачу на анализ таблицы истинности. В нашем примере используется только четыре переменные, в задачах ЕГЭ (B2) их может быть больше, но логика решения подобная.
Задача1: Ученик заполнил лишь частично таблицу истинности для выражения Z.
| X1 | X2 | X3 | X4 | Z |
| 1 |
|
| 0 | 1 |
|
| 1 | 0 |
| 0 |
Каким может быть выражение Z?
x1/\ ¬x2/\ ¬x3/\ ¬x4
x1 \/ x2 \/ x3 \/ ¬x4
¬x1 /\ x2 /\ ¬x3 /\ x4
x1 \/ ¬x2 \/ x3 \/ ¬x4
Решение:
Давайте проанализируем каждое выражение.
X1/\ ¬x2/\ ¬x3/\ ¬x4
Три операции логического умножения,
Z= 1 может быть только при единичном значении каждого операнда. Так как x1=1 и ¬x4 =1, то возможно Z=1 при ¬x2=1,
Z=0, если хотя бы один операнд выражения равен 0: ¬x2=0
Выражение подходит
x1 \/ x2 \/ x3 \/ ¬x4
Три операции логического сложения.
Z=1, если хотя бы один операнд равен 1. x1=1
Z=0, если все операнды равны 0. Но ¬x3=1.
Выражение не подходит
3) ¬x1 /\ x2 /\ ¬x3 /\ x4
Три операции логического умножения,
Z= 1 только при единичном значении каждого операнда. Т.к. x1=1, x4 =0, то Z≠ 1.
Выражение не подходит
4) x1 \/ ¬x2 \/ x3 \/ ¬x4
Три операции логического сложения. Z=1, если хотя бы один операнд равен 1.
x1=1; ¬x4=1
Z=0, если все операнды равны 0: x3=0, ¬x2=0
Выражение подходит
Ответ: 1) 4)
Кто может предложить свой ход решения этой задачи?
(Рассматриваются варианты учащихся)
Порядок действий в арифметических и алгебраических выражениях вы хорошо знаете из уроков математики. Давайте вспомним порядок выполнения логических операций, он очень напоминает алгебраический. (Показ слайда «Порядок следования операций»
Рассмотрим задачу поиска длины отрезка. ( ЕГЭ - B18)
Задача 2: На числовой прямой даны два отрезка: P = [24; 55] и Q = [40; 61]. Укажите наименьшую возможную длину такого отрезка A, что формула (x P) → ((x Q) /\ ¬(x A) ) истинна при любом значении переменной х, т.е. принимает значение 1 при любом значении переменной х.
Решение:
Чтобы выражение было всегда истинно для операции импликации второй операнд (x Q) /\ ¬(x A) не должен быть ложным (≠0). Логическое умножение всегда истинно, если оба операнда истинны, т.е. (x Q)=1 и ¬(x A)=1, т.е. (x Q)= ¬(x A). A∉ Q, но, AP, значит A лежит в их общей области (24; 40)
Ответ: A=(24; 40)
Предлагаю вам в тетрадях решить подобную задачу. На доске её будет решать Ф. И. ученика.
Задача3: На числовой прямой даны два отрезка P(2, 12) и Q (7,23), укажите наименьшую возможную длину такого отрезка A, при котором формула тождественно истинна, т.е. принимает значение 1 при любом значении переменной X.
P Q
2 7 A 12 23
¬ (X ∈ P) V (X ∈ Q )& ( X ∈ A)
Решение:
¬ (X ∈ P) – ложь (0)
Выражение будет истинно, если (X ∈ Q )& ( X ∈ A) истинно, т.е. должно ( X ∈ A) =1, одновременно X ∈ Q и X ∈ P, значит, A лежит в их общей области (7,12)
Ответ: A ( 7, 12)
Логические выражения (высказывания) можно преобразовывать, для этого необходимо знать логические законы. Какие законы вы помните?
Показ слайдов «Логические законы"
Задача 4: Упростить логическое выражение X&Y v X&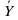 & Zv
& Zv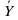 & X &
& X &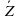 v X &
v X &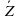
Решение: Для удобства преобразования выражения, можно поменять v (логическое сложение) на + и & ( логическое умножение) на *
X*Y+X*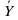 *Z+
*Z+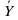 *X*
*X*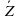 +X*
+X*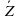 = X*Y+X
= X*Y+X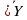 *(Z+
*(Z+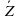 ) + X*
) + X*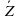 = X*Y+ X
= X*Y+ X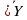 *1+ X*
*1+ X*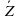 =
=
X*( Y+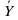 +
+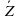 )=X*
)=X*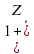 =X
=X
Выполнение самостоятельной работы.
Вариант 1 Вариант 2
((XvY) & 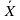 ) v ((
) v ((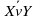 ) &
) & 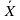 ) (X&Y)v(
) (X&Y)v(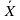 &
&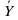 )&(Xv
)&(Xv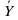 )
)
Проверка на интерактивной доске после решения в тетради.
5. Постановка домашнего задания.
Решить задачу:
Александра заполняла таблицу истинности для выражения F. Она успела заполнить лишь небольшой фрагмент таблицы:
| X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | F |
|
| 0 |
|
|
|
|
| 0 | 0 |
| 1 |
|
| 0 |
|
|
|
| 1 |
|
|
|
| 1 |
|
|
| 1 | 1 |
Каким выражением может быть F?
1) x1 /\ ¬x2 /\ x3 /\ ¬x4 /\ x5 /\ x6 /\ ¬x7 /\ ¬x8
2) x1 \/ x2 \/ x3 \/ ¬x4 \/ ¬x5 \/ ¬x6 \/ ¬x7 \/ ¬x8
3) ¬x1 /\ x2 /\ ¬x3 /\ x4 /\ x5 /\ ¬x6 /\ x7 /\ x8
4) x1 \/ ¬x2 \/ x3 \/ ¬x4 \/ ¬x5 \/ ¬x6 \/ ¬x7 \/ ¬x8
6. Подведение итогов урока.
Сегодня мы завершили изучение основ логики, что позволит вам быть успешными при решении задач ЕГЭ по информатике в этом разделе.
Оценка знаний учащихся, аргументация выставленных оценок.
Литература
Семакин И.Г. Информатика и ИКТ: учебник для 10-11 классов – М.: Бином. Лаборатория знаний, 2008.
Семакин И.Г., Хеннер Е.К. Информатика и ИКТ. Задачник-практикум. Ч. 1, 2. – М.: Бином. Лаборатория знаний, 2009
Демонстрационный вариант контрольных измерительных материалов единого государственного экзамена 2015 года по информатике и ИКТ.

 Получите свидетельство
Получите свидетельство Вход
Вход











 Разработка урока информатики "Основы логики" 11 класс (41.15 KB)
Разработка урока информатики "Основы логики" 11 класс (41.15 KB)
 0
0 1275
1275 143
143 Нравится
0
Нравится
0




