Раздаточный материал (для каждого ученика)
Фамилия Имя ученика _______________________класс____
| Номер учебного элемента, время | Учебный материал с указанием заданий | Руководство по усвоению учебного содержания | |||||||||||||||||
| Блок 1. Аксиомы стереометрии
5 минут
6 минут
4 минуты | 1. Сформулируйте три аксиомы о взаимном расположении точек, прямых и плоскостей. 1. Аксиомы стереометрии
2. Как формулируются следствия из этих аксиом? Следствия из аксиом стереометрии.
Задание 1. Как в пространстве можно однозначно задать плоскость? Способы задания плоскостей.
- Почему штатив фотоаппарата имеет три ножки, а не более?
| Учащиеся вспоминают учебный материал (при необходимости пользуются учебником) и составляют опорный конспект.
Учащиеся составляют таблицы.
Учащиеся самостоятельно выполняют задание Пары обмениваются решениями и проверяют работы друг друга, сверяясь со слайдом Критерии: всё правильно – 3 балла, 1 ошибка– 2 балла, более 2 ошибок – 0 баллов. | |||||||||||||||||
| После обсуждения теоретических вопросов закрепление полученных знаний. Задание 2. Ответьте на вопросы Сколько плоскостей можно провести через выделенные элементы?
г) д) е) |
Учащиеся самостоятельно выполняют задание Пары обмениваются решениями и проверяют работы друг друга, сверяясь со слайдом Критерии: Всё правильно – 3 балла, | ||||||||||||||||||
| Задание 3. Определите: верно, ли утверждение?
| Учащиеся самостоятельно выполняют задание Пары обмениваются решениями и проверяют работы друг друга, ученики по очереди объясняют свое решение, сверяясь со слайдом Всё правильно – 3 балла, | ||||||||||||||||||
| Задание 4. (3 балла) Три вершины параллелограмма лежат в некоторой плоскости. Можно ли утверждать, что и его четвертая вершина лежит в этой плоскости? | Учащиеся самостоятельно выполняют задание Пары обмениваются решениями и проверяют работы друг друга, ученики по очереди объясняют свое решение по чертежу на слайде. | ||||||||||||||||||
| Задание 5. Докажите, что все вершины четырехугольника АВСD лежат в одной плоскости, если его диагонали АС и ВD пересекаются. | дополнительное
(4 балла) | ||||||||||||||||||
| Блок– 2. Параллельные прямые в пространстве.
5 минут 6 минут 4 минуты | Актуализация опорных знаний. Проведем теоретическую разминку.
- Взаимное расположение в пространстве двух прямых. - Какие прямые в пространстве называются параллельными? - Сформулируйте признак параллельности прямых в пространстве. - Сформулируйте свойство параллельных прямых в пространстве. - Какие прямые в пространстве называются параллельными? - Доказать признак параллельности прямых в пространстве, свойство параллельных прямых в пространстве
| Учащиеся вспоминают учебный материал (при необходимости пользуются учебником) и составляют опорный конспект. Один ученик доказывает признак параллельности прямых в пространстве, второй ученик доказывает свойство параллельных прямых в пространстве по чертежу на слайде.
| |||||||||||||||||
| После обсуждения теоретических вопросов закрепление полученных знаний.
Задание 1 Вставьте пропущенные слова
1) Единственную плоскость можно задать через три точки, при этом они … на одной прямой. 4) Прямые являются … в пространстве, если они не пересекаются и … в одной плоскости. 5) Если прямая a лежит в плоскости α, прямая b не лежит в плоскости α, но пересекает ее в точке В | Учащиеся самостоятельно выполняют задание Пары обмениваются решениями и проверяют работы друг друга, ученики по очереди объясняют свое решение, сверяясь со слайдом Критерии: Всё правильно – 3 балла,
| ||||||||||||||||||
| Задание 2 Определите: верно, ли утверждение?
| Учащиеся самостоятельно выполняют задание Пары обмениваются решениями и проверяют работы друг друга, сверяясь со слайдом
Критерии: всё правильно – 3 балла,
| ||||||||||||||||||
| Задание 3. Тест. 1.Прямые а и b скрещиваются с прямой с. Что можно сказать о прямых а и b? а) взаимное расположение точно определить нельзя; б) скрещиваются или параллельны; в) параллельны или пересекаются; г) совпадают; д) пересекаются или скрещиваются. 2. Выберите верное утверждение. а) Две прямые называются параллельными, если они не имеют общих точек; б) две прямые, параллельные третьей прямой, параллельны; в) две прямые, перпендикулярные третьей прямой, параллельны; 3. Прямая а, параллельная прямой b, пересекает плоскость α. Прямая с параллельна прямой b, тогда: а) прямые а и с пересекаются; б) прямая с лежит в плоскости α; в) прямые а и с скрещиваются; г) прямая b лежит в плоскости α; д) прямые а и с параллельны. 4. Каким может быть взаимное расположение прямых а и b, если через прямую а можно провести плоскость, параллельную прямой b? а) скрещиваются или пересекаются; б) пересекаются или параллельны; в) скрещиваются или параллельны; г) только скрещиваются; д) только параллельны. 5. Если две прямые не скрещиваются, то они а) лежат в одной плоскости; б) только пересекаются; в) совпадают; г) только параллельны. | Учащиеся самостоятельно выполняют задание
Пары обмениваются решениями и проверяют работы друг друга, ученики по очереди объясняют свое решение.
Критерии: всё правильно – 3 балла, | ||||||||||||||||||
| З Дано: ВС=АС, СС1 АА1, АА1=22 см Найти: СС1 адание 4.
| Учащиеся самостоятельно выполняют задание
Пары обмениваются решениями и проверяют работы друг друга, ученики по очереди объясняют свое решение, сверяясь со слайдом Задача (3 балла) | ||||||||||||||||||
| Задание 5. Отрезок АВ не пересекается с плоскостью α. Через концы отрезка АВ и его середину точку М проведены параллельные прямые, пересекающие плоскость α в точках А1, В1 и М1. а) Докажите, что точки А1, В1 и М1 лежат на одной прямой. б) Найдите АА1, если ВВ1 = 12см, ММ1= 8см. | дополнительное
Задача (4 балла) | ||||||||||||||||||
| Блок – 3. Взаимное расположение в пространстве прямой и плоскости. 5 минут 3 минуты 6 минут | Актуализация опорных знаний.
- Взаимное расположение в пространстве прямой и плоскости. - Какие прямая и плоскость называются параллельными? -Сформулируйте признак параллельности прямой и плоскости в пространстве. - Доказать признак параллельности прямой и плоскости в пространстве по чертежу на слайде. | Учащиеся вспоминают учебный материал (при необходимости пользуются учебником) и составляют опорный конспект. | |||||||||||||||||
| После обсуждения теоретических вопросов закрепление полученных знаний. Задание 1 Тест. 1. Прямые а и b параллельны одной плоскости . Как расположены прямые а и b относительно друг друга? а) параллельны б) пересекаются в) скрещиваются 2. Прямые а и b параллельны. Через каждую из них проведено по плоскости, которые пересекаются по прямой с. Как расположена прямая с по отношению к прямым а и b? а) параллельно б) пересекает в) перпендикулярно 3. Прямая а лежит в плоскости . Как расположена относительно плоскости прямая b, если b параллельна а? а) перпендикулярно б) параллельно в) пересекает 4. Сколько плоскостей можно провести через две данные точки? а) одну б) две в) много 5. Если одна из двух параллельных прямых пересекает плоскость, то другая прямая а) параллельна плоскости б) пересекает плоскость в) перпендикулярна плоскости 7. Точка А принадлежит плоскости α, точка В не принадлежит плоскости α. Принадлежит ли плоскости середина отрезка АВ. а) да б) нет в) не всегда 8. Прямая а параллельна прямой в, а прямая в параллельна с плоскостью . Взаимное расположение прямой а и плоскости . а) параллельны б) пересекаются в) скрещиваются г) совпадают | Учащиеся выполняют задание самостоятельно.
Пары обмениваются решениями и проверяют работы друг друга, ученики по очереди устно объясняют свое решение. Критерии: Всё правильно – 3 балла, | ||||||||||||||||||
| З Дано: а çç α а β; β ∩ α = в Доказать: а çç в
| Учащиеся самостоятельно выполняют задание Пары обмениваются решениями и проверяют работы друг друга | ||||||||||||||||||
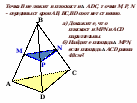
| Задание 3 (3 балла) Плоскость проходит через сторону АС D АВС. Точки D и E - середины отрезков АВ и BC соответственно. Докажите, что DE çç α.
| Учащиеся самостоятельно выполняют задание Пары обмениваются решениями и проверяют работы друг друга | ||||||||||||||||||
| Задание 4 | дополнительное Задача (3 балла) | ||||||||||||||||||
| З В адание 5 А 7см
α  D С
8см
К | дополнительное Задача (4 балла) | ||||||||||||||||||
| Блок – 4. Взаимное расположение в пространстве двух плоскостей. 15 минут 5 минут 6 минут | Актуализация опорных знаний. Проведем теоретическую разминку.
α - Взаимное расположение в пространстве двух плоскостей. - β β α Какие плоскости называются параллельными?- На практике в столовой, где встречаетесь с параллельными плоскостями? - Сформулируйте признак параллельности плоскостей в пространстве - Сформулируйте теорему о существовании плоскости, параллельной данной плоскости. - Доказать признак параллельности плоскостей в пространстве, теорему о существовании плоскости, параллельной данной плоскости по чертежу на слайде - Сформулируйте свойства параллельных плоскостей. - По чертежу на слайде доказать свойства параллельных плоскостей.
а β | Учащиеся вспоминают учебный материал (при необходимости пользуются учебником) и составляют опорный конспект. | |||||||||||||||||
| После обсуждения теоретических вопросов закрепление полученных знаний.
Задание 1 Тест. 1. Плоскость α параллельна прямой в, а прямая в параллельна плоскости . Взаимное расположение плоскостей α и . а) параллельны б) пересекаются в) совпадают 2. Плоскость пересекает плоскости α и β по параллельным прямым а и в. Взаимное расположение плоскостей α и β. а) параллельны б) пересекаются в) совпадают 3. Каждая из плоскостей α и β параллельна плоскости . Взаимное расположение плоскостей α и β. а) параллельны б) пересекаются в) совпадают 4. Каждая из плоскостей α и β параллельна прямой а. Взаимное расположение плоскостей α и β. а) параллельны б) пересекаются в) совпадают | Учащиеся выполняют задание самостоятельно.
Пары обмениваются решениями и проверяют работы друг друга, ученики по очереди устно объясняют свое решение.
Критерии: Всё правильно – 3 балла, | ||||||||||||||||||
| Задание 2 Верно ли, что
| Учащиеся выполняют задание самостоятельно. Пары обмениваются решениями и проверяют работы друг друга, ученики по очереди устно объясняют свое решение. Критерии: Всё правильно – 3 балла,
| ||||||||||||||||||
| Задание 3 Задача 1. Через данную точку А провести плоскость, параллельную данной плоскости α, не проходящей через точку А.
3 балла
| Учащиеся выполняют задание самостоятельно. Пары обмениваются решениями и проверяют работы друг друга | ||||||||||||||||||
| Задание 4 Задача2. Докажите, что через каждую из двух скрещивающихся прямых можно провести плоскость так, чтобы эти плоскости были параллельны.
4 балла
| Учащиеся выполняют задание самостоятельно. Пары обмениваются решениями и проверяют работы друг друга | ||||||||||||||||||
| Задание 5 Задача 3. Через данную прямую а провести плоскость, параллельную другой данной прямой b. | дополнительное Задача (4 балла) | ||||||||||||||||||
| | Критерии: 35 – 46 баллов - 5, Дополнительные задачи оцениваются отдельно. | Учащиеся подсчитывают свои баллы и выставляют себе оценки.
Тетради сдаются учителю для коррекции оценок. | |||||||||||||||||
| 4. Контроль знаний и способов действий 15 минут | Самостоятельная работа 1. Средняя линия трапеции лежит в плоскости α. Пересекают ли прямые, содержащие ее основания, плоскость α? (Нет, т.к. средняя линия трапеции параллельна основаниям. Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна самой плоскости - признак параллельности прямой и плоскости в пространстве.) 2. Докажите, что если данная прямая параллельна двум пересекающимся плоскостям, то она параллельна линии их пересечения 3.
| Задание выполняется на подготовленных подписанных листочках. Оценки за самостоятельную работу объявляются на следующем уроке. | |||||||||||||||||
| 5. Рефлексия. |
| Выберите нужный смайлик. | |||||||||||||||||
| 6. Задание на дом. | Домашнее задание зависит от качества работы на уроке. Если ученик отработал все учебные элементы и набрал максимальное количество баллов, то ему нет необходимости выполнять домашнее задание. Если же в ходе классной работы допускались ошибки, то рекомендуется повторить тот или иной учебный материал и решить оставшиеся задачи. | |

 Получите свидетельство
Получите свидетельство Вход
Вход



 а) б) в)
а) б) в)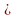 α, то прямые а и b …
α, то прямые а и b …














 Раздаточный материал по теме "Параллельность прямых и плоскостей" (5.69 MB)
Раздаточный материал по теме "Параллельность прямых и плоскостей" (5.69 MB)
 0
0 301
301 5
5 Нравится
0
Нравится
0


