Рабочие программы по алгебре для 7 – 11 классов
Учебник - Алимов Ш.А.
Оглавление
Пояснительная записка к рабочей программе по предмету «АЛГЕБРА» в 7 классе
Цели и задачи
Требования к уровню подготовки учащихся
Технологии обучения и формы уроков
Место учебного предмета «АЛГЕБРА» в учебном плане школы
Содержание программы по разделам с указанием контрольных и самостоятельных работ, презентаций с применением ИКТ, количества часов по разделам
Тематическое планирование.
Формы и средства контроля.
Перечень учебно-методических средств обучения
Формы периодического контроля знаний
Нормы оценки знаний
ПРИЛОЖЕНИЕ 1
Уровень подготовки
Пояснительная записка
Рабочая программа по курсу «АЛГЕБРА» составлена на основе федерального компонента государственного стандарта среднего(полного) общего образования приказом МО РФ № 1312 от 09.03.2004 г.
Нормативная основа программы
Закон РФ «Об образовании в РФ» от 4 января 2013 г.
Приказ Министерства образования и науки Российской Федерации от 17 декабря 2010 г. N 1897 "Об утверждении федерального государственного образовательного стандарта основного общего образования»,
«Требования к структуре основной образовательной программы основного общего образования» ФГОС основного общего образования, раздел III, пункт 18.2.2 Приказа Министерства образования и науки от 17.12.2012 № 1897,
Приказ Министерства образования и науки Российской Федерации от 17 мая 2012 года № 413 «Об утверждении федерального государственного образовательного стандарта среднего (полного) общего образования».
Цели и задачи
Школьное математическое образование ставит следующие цели обучения:
овладение конкретными математическими знаниями, необходимыми для применения в практической деятельности, для изучения смежных дисциплин, для продолжения образования;
интеллектуальное развитие учащихся, формирование качеств мышления, характерных для математической деятельности и необходимых для повседневной жизни;
формирование представлений об идеях и методах математики, о математике как форме описания и методе познания действительности;
формирование представлений о математике как части общечеловеческой культуры, понимания значимости математики для общественного прогресса.
При этом решаются следующие задачи:
развитие представление о числе, роли вычислений в человеческой практике; формирование практических навыков выполнения устных, письменных, инструментальных вычислений, развитие вычислительной культуры;
овладение символическим языком алгебры, выработка формально-оперативные алгебраических умений и применение их к решению математических и нематематических задач;
изучение свойств и графиков элементарных функций, научиться использовать функционально-графические представления для описания и анализа реальных зависимостей;
развитие пространственных представлений и изобразительных умений, освоение основных фактов и методов планиметрии, знакомство с простейшими пространственными телами и их свойствами;
получение представления о закономерностях в реальном мире и о различных способах их изучения.
развитие логического мышления и речи – умения логически обосновывать суждения, проводить несложные систематизации, приводить примеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства;
Требования к уровню подготовки учащихся
В рабочей программе представлено тематическое содержание курса алгебры для 7 класса по учебнику Алимова Ш.А.(, Алимов Ш.А. и др. Алгебра. Учебник для 7 класса общеобразовательных учреждений. М., «Просвещение», 2008.).
Для каждого раздела указываются конкретные требования к обязательному и возможному уровню подготовки обучающегося, виды контроля, примеры и задачи.
Уровень обязательной подготовки обучающегося для прохождения курса алгебра в 7 классе.
Уметь выполнять действия с натуральными числами.
Уметь выполнять действия с обыкновенными дробями.
Уметь выполнять действия с десятичными дробями.
Уметь решать текстовые задачи.
В РЕЗУЛЬТАТЕ ОБУЧЕНИЯ УЧЕНИК ДОЛЖЕН:
уметь
составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, выражать из формул одну переменную через другую;
выполнять основные действия со степенями с натуральным показателями; с многочленами; выполнять разложение многочленов на множители; выполнять тождественные преобразования целых выражений;
решать линейные уравнения, системы двух линейных уравнений;
решать задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;
определять координаты точки плоскости, строить точки с заданными координатами;
находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;
строить графики изученных функций;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
выполнения расчетов по формулам, для составления формул, выражающих зависимости между реальными величинами; для нахождения нужной формулы в справочных материалах;
моделирования практических ситуаций и исследовании построенных моделей с использованием аппарата алгебры;
интерпретации графиков реальных зависимостей между величинами;
Технология обучения и формы уроков
Система уроков условна, но все же выделяются следующие виды:
Урок-лекция. Предполагаются совместные усилия учителя и учеников для решения общей проблемной познавательной задачи. На таком уроке используется демонстрационный материал на компьютере, разработанный учителем или учениками, мультимедийные продукты.
Урок-практикум. На уроке учащиеся работают над различными заданиями в зависимости от своей подготовленности. Виды работ могут быть самыми разными: письменные исследования, решение различных задач, изучение свойств различных функций, практическое применение различных методов решения задач. Компьютер на таких уроках используется как электронный калькулятор, тренажер устного счета, виртуальная лаборатория, источник справочной информации.
Урок-исследование. На уроке учащиеся решают проблемную задачу исследовательского характера аналитическим методом и с помощью компьютера с использованием различных лабораторий.
Комбинированный урок предполагает выполнение работ и заданий разного вида.
Урок решения задач. Вырабатываются у учащихся умения и навыки решения задач на уровне обязательной и возможной подготовке.
Урок-тест. Тестирование проводится с целью диагностики пробелов знаний, контроля уровня усвоения материала учащимися, тренировки технике тестирования. Тесты предлагаются как в печатном, так и в компьютерном варианте.
Урок-зачет. Устный опрос учащихся по заранее составленным вопросам, а также решение задач разного уровня по изученной теме.
Урок-самостоятельная работа. Предлагаются разные виды разноуровневых самостоятельных работ.
Урок-контрольная работа. Проводится на двух уровнях:
уровень обязательной подготовки - «3», уровень возможной подготовки - «4» и «5».
Компьютерное обеспечение уроков.
В разделе рабочей программы «Компьютерное обеспечение» спланировано применение имеющихся компьютерных продуктов: демонстрационный материал, задания для устного опроса учащихся, тренировочные упражнения, а также различные электронные учебники.
Демонстрационный материал (слайды).
Создается с целью обеспечения наглядности при изучении нового материала, использования при ответах учащихся. Изучение многих тем в математике связано с знанием и пониманием свойств элементарных функций. Решение уравнений, неравенств, различных задач предполагает глубокое знание поведения элементарных функций. Научиться распознавать графики таких функций, суметь рассказать об их свойствах помогают компьютерные слайды .
При решении любых задач использование графической интерпретации условия задачи, ее решения позволяет учащимся понять математическую идею решения, более глубоко осмыслить теоретический материал по данной теме.
Задания для устного счета.
Эти задания дают возможность в устном варианте отрабатывать различные вопросы теории и практики, применяя принципы наглядности, доступности. Их можно использовать на любом уроке в режиме учитель – ученик, взаимопроверки, а также в виде тренировочных занятий.
Электронные учебники.
Они используются в качестве виртуальных лабораторий при проведении практических занятий, уроков введения новых знаний. В них заключен большой теоретический материал, практических и исследовательских заданий, справочного материала. На уроках возможно использование компьютерных устных упражнений, применение тренажера устного счета.
Использование компьютерных технологий в преподавании математики позволяет непрерывно менять формы работы на уроке, постоянно чередовать устные и письменные упражнения, осуществлять разные подходы к решению математических задач, а это постоянно создает и поддерживает интеллектуальное напряжение учащихся, формирует у них устойчивый интерес к изучению данного предмета.
Место предмета «АЛГЕБРА» в учебном плане школы
Согласно школьному базисному учебному плану для изучения алгебры в 7 классе отводится не менее 68 часов из расчета 2 часов в неделю. Независимо от профильной направленности школы и класса алгебра является обязательным предметом, в виду необходимости сдавать экзамен за 9, а затем и 11 классы.
Содержание программы
Тема 1 Повторение. Краткое повторение основных разделов математики 5 и 6 классов.. Действие с дробями и методы решения задач на движение, производительность труда и др., 3 часа,
Тема 2 Алгебраические выражения. Численные вычисления. Преобразование простых алгебраических выражений. 7 часов. 2 С.р., 1 К.р.
Тема 3 Уравнения с одним неизвестным. Решение линейного уравнения. Решение текстовых задач на составление линейного уравнения. 5 часов. 1 К.р.
Тема 4 Одночлены и многочлены. Степень одночленов. Раскрытие скобок. Приведение подобных слагаемых. Сложение многочленов. Умножение одночленов. Умножение многочленов, 12 часов. 2 С.р. , 1 К.р.
Тема 5 Разложение многочленов на множители. Разложение многочлена на простые множители методом группировки. Вывод формул сокращенного умножения и их применение при разложении многочлена на множители. 7 часов. 2 С.р., 1 К.р.
Тема 6 Алгебраические дроби. Сложение, вычитание, умножение и деление алгебраических дробей. 9 часов. 4 С.р., 1 К.р.
Тема 7 Линейные функции и их графики. Декартова система координат. Связь независимой зависимой переменными. Общая запись линейной функции. Построение графиков линейной функции по координатам точек. 7 часов.» С.р.
Тема 8 Системы дух линейных уравнений с двумя переменными. Методы решения систем линейных уравнений: подстановка, выравнивание коэффициентов, графический способ. 8 часов, 2 С.р., 1 К.р.
Тема 9 Введение в комбинаторику. Первичное понятие вероятности события. Способом переборки вариантов нахождение количества положительных событий при выборке из общего числа К-элементов по М-элементов, где М меньше К. 2 часа
Тема 10 Повторение. 11 часов, 1 С.р., 1 К.р.
Контрольные работы по темам приведены в ПРИЛОЖЕНИИ 2 к Рабочей программе
Тематическое планирование (учебник АЛГЕБРА для 7 класса общеобразовательных учреждений. Авт.: Ш.А. Алимов и др.).
| № урока | Темы | контроль | № учебной недели |
|
| Тема 1 Повторение 3 часа |
|
|
| 1 | Основные разделы математики 5 и 6 классов. |
| 1 |
| 2 | Все действия с дробями. |
| 1 |
| 3 | Задачи на движение и производительность. |
| 2 |
|
| Тема 2 Алгебраические выражения. 7 часов |
|
|
| 4 | Числовые и алгебраические выражения. |
| 2 |
| 5 | Алгебраические равенства. |
| 3 |
| 6 | Формулы. Самостоятельная работа. | С.р. | 3 |
| 7 | Арифметические действия с буквенными выражениями. |
| 4 |
| 8 | Правила раскрытия скобок. Самостоятельная работа. | С.р. | 4 |
| 9 | Решение примеров. |
| 5 |
| 10 | Контрольная работа №1 | К.р. | 5 |
|
| Тема 3 Уравнения с одним неизвестным. 5 часов |
|
|
| 11 | Уравнения и его корни. |
| 6 |
| 12 | Решение линейных уравнений. |
| 6 |
| 13 | Решение текстовых задач на составление уравнения. |
| 7 |
| 14 | Решение примеров и задач. |
| 7 |
| 15 | Контрольная работа №2 | К.р. | 8 |
|
| Тема 4 Одночлены и многочлены. 12 часов |
|
|
| 16 | Степень с натуральным показателем. |
| 8 |
| 17 | Свойства степени с натуральным показателем. |
| 9 |
| 18 | Стандартный вид одночлена. |
| 9 |
| 19 | Умножение одночленов. Самостоятельная работа. | С.р. | 10 |
| 20 | Многочлены. |
| 10 |
| 21 | Приведение подобных членов. |
| 11 |
| 22 | Сложение и вычитание многочленов. |
| 11 |
| 23 | Умножение одночлена на многочлен. |
| 12 |
| 24 | Умножение многочлена на многочлен. Самостоятельная работа. | С.р. | 12 |
| 25 | Деление на одночлен. |
| 13 |
| 26 | Решение примеров. |
| 13 |
| 27 | Контрольная работа № 3 | К.р. | 14 |
|
| Тема 5 Разложение многочленов на множители. 7 часов |
|
|
| 28 | Вынесение общего члена за скобки. |
| 14 |
| 29 | Способ группировки. |
| 15 |
| 30 | Разность квадратов. Вывод формулы. Самостоятельная работа. | С.р. | 15 |
| 31 | Квадрат суммы и квадрат разности. Вывод формул. Самостоятельная работа. | С.р. | 16 |
| 32 | Разложение на множители разными способами. |
| 16 |
| 33 | Решение примеров. |
| 17 |
| 34 | Контрольная работа №4 | К.р. | 17 |
|
| Тема 6 Алгебраические дроби. 8 часов |
|
|
| 35 | Алгебраическая дробь. |
| 18 |
| 36 | Сокращение дробей. Самостоятельная работа. | С.р. | 18 |
| 37 | Приведение дробей к общему знаменателю. |
| 19 |
| 38 | Сложение и вычитание алгебраических дробей. |
| 19 |
| 39 | Умножение и деление алгебраических дробей. Самостоятельная работа. | С.р. | 20 |
| 40 | Совместные действия с алгебраическими дробями. |
| 20 |
| 41 | Решение примеров. |
| 21 |
| 42 | Контрольная работа №5 | К.р. | 21 |
|
| Тема 7 Линейные функции и их графики. ? часов |
|
|
| 43 | Прямоугольная система координат. |
| 22 |
| 44 | Понятие функции и аргумента. |
| 22 |
| 45 | Координаты точек в системе координат. |
| 23 |
| 46 | Функция Y = kX . График функции. |
| 23 |
| 47 | Графики линейных функций. |
| 24 |
| 48 | Решение примеров и задач. |
| 24 |
| 49 | Контрольная работа №7 | К.р. | 25 |
|
| Тема 8 Системы дух линейных уравнений с двумя переменными. 6 часов |
|
|
| 50 | Системы линейных уравнений. |
| 25 |
| 51 | Методы решения систем линейных уравнений. Способ подстановки. Самостоятельная работа. | С.р. | 26 |
| 52 | Способ сложения и вычитания или метод выравнивания коэффициентов. Самостоятельная работа. | С.р. | 26 |
| 53 | Графический способ решения системы линейных уравнений. |
| 27 |
| 54 | Решение примеров. |
| 27 |
| 55 | Контрольная работа №8 | К.р. | 28 |
|
| Тема 9 Введение в комбинаторику. 2 часа |
|
|
| 56 | Первичное понятие вероятности события. |
| 28 |
| 57 | Способом переборки вариантов нахождение количества положительных событий. |
| 29 |
|
| Тема 10 Повторение. 11 часов
|
|
|
| 58 | Сложение и вычитание многочленов. |
| 29 |
| 59 | Умножение многочлена на многочлен. |
| 30 |
| 60 | Деление многочлена на одночлен. |
| 30 |
| 61 | Формулы сокращенного умножения. |
| 31 |
| 62 | Разложение многочлена на множители. |
| 31 |
| 63 | Действия с алгебраическими дробями. |
| 32 |
| 64 | Линейные функции. Графики. Самостоятельная работа. | С.р. | 32 |
| 65 | Решение систем линейных уравнений. |
| 33 |
| 66 | Решение примеров. |
| 33 |
| 67 | Решение текстовых задач. |
| 34 |
| 68 | Итоговая контрольная работа. | К.р. | 34 |
| 69-70 | Резерв времени |
| 35 |
Самостоятельных работ - 10
Контрольных работ - 9
Формы и средства контроля.
Основными методами проверки знаний и умений учащихся по алгебре являются устный опрос, письменные работы. К письменным формам контроля относятся: математические диктанты, самостоятельные и контрольные работы, тесты. Основные виды проверки знаний – текущая и итоговая. Текущая проверка проводится систематически из урока в урок, а итоговая – по завершении темы (раздела), школьного курса. Варианты проверочных работ по каждой теме дан в ПРИЛОЖЕНИИ 2
Типы индивидуальных консультаций и прием зачетов
Выявление и ликвидация пробелов в знаниях обучающихся
Подготовка к изучению нового материала
Решение задач практического содержания и задач повышенной трудности
Подготовка к контрольной работе
Формы и методы проведения зачета:
Устно-индивидуальный опрос по карточкам-заданиям
Тест
Групповое собеседование
Письменный зачет
Устно-письменный зачет
Письменные ответы на вопросы
Перечень учебно-методических средств обучения
Для учащихся:
Алимов Ш.А. и др. Алгебра. Учебник для 7 класса общеобразовательных учреждений. М., «Просвещение», 2008.).
Для учителя:
Коваленко В.Г., Дидактические игры на уроках математики. Книга для учителя. М.: «Просвещение», 1990
Макарова Л.В. Математические диктанты в VII-VIII классах «Математика в школе»,1999. №3,с.27
Буланова Л. М., Дудницын Ю. П. Проверочные задания по математике для учащихся 5-8 и 10 классов. – М.: Просвещение, 1998.
Жохов В. И., Макарычкв Ю. Н., Миндюк Н. Г. Дидактические материалы по алгебре, 7 класс. – М.: Просвещение, 2000
Денищева Л.О и др. Зачёты в системе дифференцированного обучения математике.- М.: Просвещение, 1993.
Зив Б.Г. и др. Задачи по геометрии для 7-11 классов.- М.: Просвещение, 1991.
Выгодский М.Я. Справочник по элементарной математике — М.: ООО «Издательство Астрель»: ООО «Издательство АСТ», 2003.
Никольский С.Н. Математика: Школьная энциклопедия — М.: Большая Российская энциклопедия; Дрофа, 1997.
Список дополнительной литературы по вопросам комбинаторики и теории вероятностей.
Бунимович Е. А., Булычев В. А. Основы статистики и вероятность. — М., 2004.
Виленкин Н. Я. Комбинаторика. — М., 1969.
Гмурман В. Е. Теория вероятностей и математическая статистика. — М., 1997.
Гнеденко Б. В., Хинчин А. Я. Элементарное введение в теорию вероятностей. М., 1982.
Лютикас B. C. Факультативный курс по математике. Теория вероятностей. — М., 1990. 7. Мостеллер Ф. Пятьдесят занимательных вероятностных задач с решениями. М., 1985.
Плоцки А. Вероятность в задачах для школьников. — М., 1996.
Ткачева М. В., Федорова Н. Е. Элементы статистики и вероятность. Учебное пособие для учащихся 7—9 кл. — М., 2005.
Тюрин Ю. Н. и др. Теория вероятностей и статистика. — М., 2004.
Для информационной поддержки учебного процесса предполагается использовать следующие веб-узлы и учебные СД- диски
Министерство образования РФ: http://www.ed.gov.ru/ ; http://www.edu.ru
Тестирование online: 5 - 11 классы: http://www.kokch.kts.ru/cdo
Педагогическая Сеть «Методисты.ру» Математика в школе
Новые технологии в образовании: http://edu.secna.ru/main
Путеводитель «В мире науки» для школьников: http://www.uic.ssu.samara.ru
Мегаэнциклопедия Кирилла и Мефодия: http://mega.km.ru
сайты «Энциклопедий»: http://www.rubricon.ru/; http://www.encyclopedia.ru
сайт для самообразования и он-лайн тестирования: http://uztest.ru/
досье школьного учителя математики: http://www.mathvaz.ru/
Сайт учителя математики Шапошникова И.М.
ПРИЛОЖЕНИЕ 1 к РП по алгебре 7 класс. Уровень подготовки
Уровень обязательной подготовки
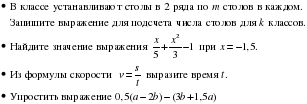
Уровень обязательной подготовки 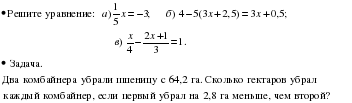
Уровень возможной подготовки 
Уровень обязательной подготовки 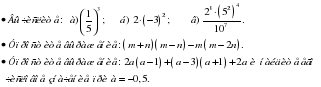
Уровень возможной подготовки 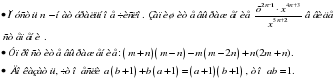
Уровень обязательной подготовки
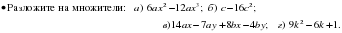
Уровень возможной подготовки
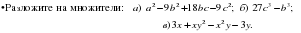
Уровень обязательной подготовки
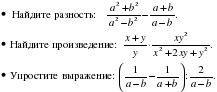
Уровень возможной подготовки
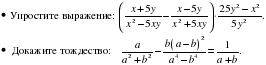
Уровень обязательной подготовки 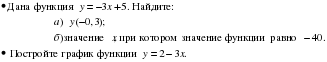
Уровень возможной подготовки
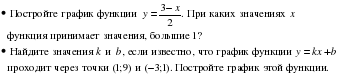
Уровень обязательной подготовки
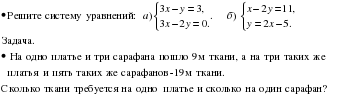
Уровень возможной подготовки 
Уровень обязательной подготовки
Сколькими способами могут разместиться 3 человека в салоне автобуса на трех свободных местах?
Сколько трехзначных чисел, в которых нет одинаковых цифр, можно составить из цифр 1, 2, 3, 4?
Из 6 членов туристической группы надо выбрать двух дежурных. Сколькими способами можно сделать такой выбор?
Уровень возможной подготовки
Из села Дятлова в село Михайловское ведут три дороги, а из села Михайловское в село Першино – четыре дороги. Сколькими способами можно попасть из Дятлова в Першино через Михайловское?
В седьмом классе изучается 15 предметов. Сколькими способами можно составить расписание на понедельник, если известно, что в этот день должно быть 6 уроков.
Обязательный минимум курса алгебра 7 класс
Уравнение с одной переменной.
Линейное уравнение
Корень уравнения.
Система двух линейных уравнений с двумя переменными; решение подстановкой и алгебраическим сложением.
Решение текстовых задач алгебраическим способом.
Уровень обязательной подготовки
Уровень возможной подготовки
Уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни для выполнения расчетов по формулам, составления формул, выражающих зависимости между реальными величинами.
Понимать, что уравнения – это математический аппарат решения разнообразных задач из математики, смежных областей знаний, практики.
Понимать, что функция – это математическая модель, позволяющая описывать и изучать разнообразные зависимости между реальными величинами.
Уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни для интерпретации графиков реальных зависимостей между величинами.
Уровень обязательной подготовки

Уровень возможной подготовки выпускника
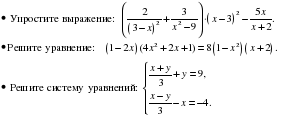

Оглавление
Пояснительная записка к рабочей программе по предмету «АЛГЕБРА» в 8 классе
Цели и задачи
2 Требования к уровню подготовки учащихся
3 Технологии обучения и формы уроков
Место учебного предмета «АЛГЕБРА» в учебном плане школы
5 Содержание программы по разделам с указанием контрольных и самостоятельных работ, презентаций с применением ИКТ, количества часов по разделам
6 Тематическое планирование.
7 Формы и средства контроля.
8 Перечень учебно-методических средств обучения
ПРИЛОЖЕНИЯ
Поурочное планирование
Применение тестов и контрольных работ по предмету «АЛГЕБРА»
Формы периодического контроля знаний
Нормы оценки знаний
Пояснительная записка
Рабочая программа по курсу «АЛГЕБРА» составлена на основе федерального компонента государственного стандарта среднего(полного) общего образования приказом МО РФ № 1312 от 09.03.2004 г.
Нормативная основа программы
1 Закон РФ «Об образовании в РФ» от 4 января 2013 г.
2 Приказ Министерства образования и науки Российской Федерации от 17 декабря 2010 г. N 1897 "Об утверждении федерального государственного образовательного стандарта основного общего образования»,
3 «Требования к структуре основной образовательной программы основного общего образования» ФГОС основного общего образования, раздел III, пункт 18.2.2 Приказа Министерства образования и науки от 17.12.2012 № 1897,
Приказ Министерства образования и науки Российской Федерации от 17 мая 2012 года № 413 «Об утверждении федерального государственного образовательного стандарта среднего (полного) общего образования».
Цели и задачи
Школьное математическое образование ставит следующие цели обучения:
овладение конкретными математическими знаниями, необходимыми для применения в практической деятельности, для изучения смежных дисциплин, для продолжения образования;
интеллектуальное развитие учащихся, формирование качеств мышления, характерных для математической деятельности и необходимых для повседневной жизни;
формирование представлений об идеях и методах математики, о математике как форме описания и методе познания действительности;
формирование представлений о математике как части общечеловеческой культуры, понимания значимости математики для общественного прогресса.
При этом решаются следующие задачи:
развитие представление о числе, роли вычислений в человеческой практике; формирование практических навыков выполнения устных, письменных, инструментальных вычислений, развитие вычислительной культуры;
овладение символическим языком алгебры, выработка формально-оперативные алгебраических умений и применение их к решению математических и нематематических задач;
изучение свойств и графиков элементарных функций, научиться использовать функционально-графические представления для описания и анализа реальных зависимостей;
развитие пространственных представлений и изобразительных умений, освоение основных фактов и методов планиметрии, знакомство с простейшими пространственными телами и их свойствами;
получение представления о закономерностях в реальном мире и о различных способах их изучения.
развитие логического мышления и речи – умения логически обосновывать суждения, проводить несложные систематизации, приводить примеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства;
Требования к уровню подготовки учащихся
В рабочей программе представлено тематическое содержание курса алгебры для 8 класса по учебнику Алимова Ш.А.(, Алимов Ш.А. и др. Алгебра. Учебник для 8 класса общеобразовательных учреждений. М., «Просвещение», 2008.).
Для каждого раздела указываются конкретные требования к обязательному и возможному уровню подготовки обучающегося, виды контроля, примеры и задачи.
Уровень обязательной подготовки обучающегося для прохождения курса алгебра в 7 классе.
Уметь выполнять действия с натуральными числами.
Уметь выполнять действия с обыкновенными дробями.
Уметь выполнять действия с десятичными дробями.
Уметь решать текстовые задачи.
В РЕЗУЛЬТАТЕ ОБУЧЕНИЯ УЧЕНИК ДОЛЖЕН:
уметь
составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, выражать из формул одну переменную через другую;
выполнять основные действия со степенями с натуральным показателями; с многочленами; выполнять разложение многочленов на множители; выполнять тождественные преобразования целых выражений;
решать линейные уравнения, системы двух линейных уравнений;
решать задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;
определять координаты точки плоскости, строить точки с заданными координатами;
находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;
строить графики изученных функций;
использовать приобретенные знания и умения в практической деятельности для:
выполнения расчетов по формулам, для составления формул, выражающих зависимости между реальными величинами; для нахождения нужной формулы в справочных материалах;
моделирования практических ситуаций с использованием аппарата алгебры;
интерпретации графиков реальных зависимостей между величинами;
Технология обучения и формы уроков
Система уроков условна, но все же выделяются следующие виды:
Урок-лекция. Предполагаются совместные усилия учителя и учеников для решения общей проблемной познавательной задачи. На таком уроке используется демонстрационный материал на компьютере, разработанный учителем или учениками, мультимедийные продукты.
Урок-практикум. На уроке учащиеся работают над различными заданиями в зависимости от своей подготовленности. Виды работ могут быть самыми разными: письменные исследования, решение различных задач, изучение свойств различных функций, практическое применение различных методов решения задач. Компьютер на таких уроках используется как электронный калькулятор, тренажер устного счета, виртуальная лаборатория, источник справочной информации.
Урок-исследование. На уроке учащиеся решают проблемную задачу исследовательского характера аналитическим методом и с помощью компьютера с использованием различных лабораторий.
Комбинированный урок предполагает выполнение работ и заданий разного вида.
Урок решения задач. Вырабатываются у учащихся умения и навыки решения задач на уровне обязательной и возможной подготовке.
Урок-тест. Тестирование проводится с целью диагностики пробелов знаний, контроля уровня усвоения материала учащимися, тренировки технике тестирования. Тесты предлагаются как в печатном, так и в компьютерном варианте.
Урок-зачет. Устный опрос учащихся по заранее составленным вопросам, а также решение задач разного уровня по изученной теме.
Урок-самостоятельная работа. Предлагаются разные виды разноуровневых самостоятельных работ.
Урок-контрольная работа. Проводится на двух уровнях:
уровень обязательной подготовки - «3», уровень возможной подготовки - «4» и «5».
Компьютерное обеспечение уроков.
В разделе рабочей программы «Компьютерное обеспечение» спланировано применение имеющихся компьютерных продуктов: демонстрационный материал, задания для устного опроса учащихся, тренировочные упражнения, а также различные электронные учебники.
Демонстрационный материал (слайды).
Создается с целью обеспечения наглядности при изучении нового материала, использования при ответах учащихся. Изучение многих тем в математике связано с знанием и пониманием свойств элементарных функций. Решение уравнений, неравенств, различных задач предполагает глубокое знание поведения элементарных функций. Научиться распознавать графики таких функций, суметь рассказать об их свойствах помогают компьютерные слайды .
При решении любых задач использование графической интерпретации условия задачи, ее решения позволяет учащимся понять математическую идею решения, более глубоко осмыслить теоретический материал по данной теме.
Задания для устного счета.
Эти задания дают возможность в устном варианте отрабатывать различные вопросы теории и практики, применяя принципы наглядности, доступности. Их можно использовать на любом уроке в режиме учитель – ученик, взаимопроверки, а также в виде тренировочных занятий.
Учебный материал на электронных носителях.
Используются для практических занятий и получения новых знаний. В них заключен большой теоретический материал, практических и исследовательских заданий, справочного материала. На уроках возможно использование компьютерных устных упражнений, применение тренажера устного счета.
Использование компьютерных технологий в преподавании математики позволяет непрерывно менять формы работы на уроке, постоянно чередовать устные и письменные упражнения, осуществлять разные подходы к решению математических задач, а это постоянно создает и поддерживает интеллектуальное напряжение учащихся, формирует у них устойчивый интерес к изучению данного предмета.
Место предмета «АЛГЕБРА» в учебном плане школы
Согласно школьному базисному учебному плану для изучения алгебры в 8 классе отводится не менее 68 часов из расчета 2 часов в неделю. Независимо от профильной направленности школы и класса алгебра является обязательным предметом, в виду необходимости сдавать экзамен за 9, а затем и 11 классы.
Формы и средства контроля.
Основными методами проверки знаний и умений учащихся по алгебре являются устный опрос, письменные работы. К письменным формам контроля относятся: математические диктанты, самостоятельные и контрольные работы, тесты. Основные виды проверки знаний – текущая и итоговая. Текущая проверка проводится систематически из урока в урок, а итоговая – по завершении темы (раздела), школьного курса. Варианты проверочных работ по каждой теме был приведен выше.
Типы индивидуальных консультаций и прием зачетов в отд. НИИФ
Выявление и ликвидация пробелов в знаниях обучающихся
Подготовка к изучению нового материала
Решение задач практического содержания и задач повышенной трудности
Подготовка к контрольной работе
Формы и методы проведения зачета:
Устно-индивидуальный опрос по карточкам-заданиям
Тест
Групповое собеседование
Письменный зачет
Устно-письменный зачет
Письменные ответы на вопросы
Содержание программы по разделам
Повторение Числовые и алгебраические дроби. Приведение подобных членов. Умножение многочленов. Разложение многочленов на простые множители. Решение линейных уравнений. Решение систем двух линейных уравнений. Графики линейных функций. 3 часа.
Неравенства. Виды неравенств. Действия с неравенствами. Решение неравенств. Неравенства с модулем. Решение систем неравенств с одной переменной. 17 часов. 5 С.р. и 2 К.р.
Приближенные вычисления. Виды погрешностей. Оценка погрешности при вычислении величин. 5 часов. 1 С.р.
Решение задач. Типы текстовых задач и способы их решения. 3 часа. 1 С.р.
Иррациональные числа. Смысл квадратного корня из числа. Свойства арифметического корня. Степени и корни числа и действия с ними. 8 часов, 1 С.р., 1 К.р.
Квадратные уравнения. Виды квадратных уравнений. Корни квадратного уравнения . Вывод формулы корней квадратного уравнения. Теорема Виета. Решение текстовых задач на составления квадратного уравнения. 14 часов, 2 С.р., 3 К.р.
Системы уравнений 2-й степени с двумя неизвестными. Методы решения: подстановка, замена переменных, графический метод. 2 часа, 1 С.р.
Квадратичные функции. Определение квадратичной функции и ее свойства. Варианты квадратичных функций. Построение графиков. 7 часов, 1 С.р., 1 К.р.
Квадратичные неравенства. Решение квадратичных неравенств. Метод разложения на множители. Метод интервалов. 4 часа, 1 С.р., 1 К. р.
Повторение. Множество действительных чисел. Квадратичные функции и неравенства. Решение типовых задач на составление квадратного уравнения. 4 часа, Заключительная контрольная работа
Тематическое планирование (алгебра 8 класс)
| № урока | Тема | контроль | № учебной недели |
|
| Тема 1 Повторение 3 часа |
|
|
| 1 | Алгебраические дроби и все действия с ними. | | 1 |
| 2 | Разложение многочленов на простые множители. | | 1 |
| 3 | Решение линейных уравнений и их систем. | | 2 |
|
| Тема 2 Неравенства 17 часов |
|
|
| 4 | Числовые неравенства и их свойства | | 2 |
| 5 | Решение числовых неравенств. Самостоятельная работа | С.р. | 3 |
| 6 | Правила сложения и умножения неравенств. | | 3 |
| 7 | Сложение и умножение неравенств. Самостоятельная работа. | С.р. | 4 |
| 8 | Примеры строгих и нестрогих неравенств. | | 4 |
| 9 | Строгие и нестрогие неравенства Самостоятельная работа. | С.р. | 5 |
| 10 | Решение неравенств с одной переменной | | 5 |
| 11 | Решение неравенств. Самостоятельная работа | С.р. | 6 |
| 12 | Система неравенств. Числовые промежутки. | | 6 |
| 13 | Контрольная работа №1 Неравенства | К.р. | 7 |
| 14 | Решение систем линейных уравнений. | | 7 |
| 15 | Решение систем. Самостоятельная работа | С.р. | 8 |
| 16 | Решение практических задач | | 8. |
| 17 | Геометрическая интерпретация решений неравенств. | | 9 |
| 18 | Уравнения и неравенства с модулем | | 9 |
| 19 | Решение уравнений и неравенств с модулем | | 10 |
| 20 | Контрольная работа. №2 | К.р. | 10 |
|
| Тема 3 Приближенное вычисление 5 часов |
|
|
| 21 | Приближенное вычисление величины. | | 11 |
| 22 | Погрешность приближения | | 11 |
| 23 | Оценка погрешности. Относительная погрешность | | 12 |
| 24 | Самостоятельная работа. Погрешность. | С.р. | 12 |
|
| Тема 4 Решение текстовых задач 3 часа |
|
|
| 25 | Основные типы текстовых задач | |
|
| 26 | Решение задач на составление уравнения | |
|
| 27 | Решение задач на составление уравнения. Самостоятельная работа. | С.р. |
|
| | Тема 5 Иррациональные числа 8 часов | |
|
| 28 | Понятие квадратного корня. | |
|
| 29 | Арифметический квадратный корень. Самостоятельная работа. | С.р. |
|
| 30 | Квадратный корень из степени | |
|
| 31 | Примеры квадратного корня из степени. Самостоятельная работа | С.р. |
|
| 32 | Квадратный корень из произведения | |
|
| 33 | Примеры квадратного корня из произведения. Самостоятельная работа | С.р. |
|
| 34 | Квадратный корень из дроби | |
|
| 35 | Контрольная работа №3 | К.р. |
|
|
| Тема 6 Квадратные уравнения 14 часов |
|
|
| 36 | Типы квадратных уравнений. | |
|
| 37 | Квадратное уравнение и его корни | |
|
| 38 | Неполные квадратные уравнения. Самостоятельная работа. | С.р. |
|
| 39 | Метод выделения полного квадрата | |
|
| 40-41 | Решение квадратных уравнений | |
|
| 42 | Контрольная работа №4 | К.р. |
|
| 43 | Приведенное квалратное уравнение. Теорема Виета | |
|
| 44 | Решение квадратных уравнение по теорема Виета. | |
|
| 45 | Контрольная работа №5 | К.р. |
|
| 46 | Биквадратное уравнение. | |
|
| 47 | Уравнения, сводящиеся к квадратному уравнению. Самостоятельная работа | С.р. |
|
| 48 | Решение задач с помощью .квадратного уравнения. | |
|
| 49 | Контрольная работа № 6 | К.р. |
|
|
| Тема 7 Системы уравнений 2 часа |
|
|
| 50 | Системы уравнением 2-йстепени | |
|
| 51 | Системы уравнением 2-йстепени. Самостоятельная работа. | С.р. |
|
|
| Тема 8 Квадратичные функции 7 часов |
|
|
| 52 | Квадратичная функция.. y = x2 | |
|
| 53-54 | Функция y=ax2 | |
|
| 55 | Функция y=ax2+bx+c | |
|
| 56 | Контрольная работа № 7 | К.р. |
|
| 57 | Построение графика квадратичной функции | |
|
| 58 | Построение графика квадратичной функции. Самостоятельная работа | С.р. |
|
| | Тема 9 Квадратичные неравенства 4 часа | |
|
| 59 | Квадратичные неравенства | |
|
| 61 | Решение квадратичных неравенств. Самостоятельная работа. | С.р. |
|
| 62 | Метод интервалов | |
|
| 63 | Контрольная работа № 8 | К.р. |
|
|
| Тема 10 Повторение 4 часа | |
|
| 65 | Действительные числа. Квадратичные функции | |
|
| 66 | Квадратичные уравнения и неравенства | |
|
| 67 | Решение примеров и задач. | |
|
| 68 | Итоговая контрольная работа | К.р. |
|
Резерв времени – 2 часа
Итого: самостоятельных работ – 13
контрольных работ – 9
Формы и средства контроля.
Основными методами проверки знаний и умений учащихся по алгебре являются устный опрос, письменные работы. К письменным формам контроля относятся: математические диктанты, самостоятельные и контрольные работы, тесты. Основные виды проверки знаний – текущая и итоговая. Текущая проверка проводится систематически из урока в урок, а итоговая – по завершении темы (раздела), школьного курса.
Типы индивидуальных консультаций и прием зачетов в отд. НИИФ
Выявление и ликвидация пробелов в знаниях обучающихся
Подготовка к изучению нового материала
Решение задач практического содержания и задач повышенной трудности
Подготовка к контрольной работе
Формы и методы проведения зачета:
Устно-индивидуальный опрос по карточкам-заданиям
Тест
Групповое собеседование
Письменный зачет
Устно-письменный зачет
Письменные ответы на вопросы
Перечень учебно-методических средств обучения
Для учащихся:
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.Н., Суворова С.Б. Алгебра. Учебник для 7 класса общеобразовательных учреждений, под ред. Теляковского С.А. - М.: «Просвещение», 2010
Алимов Ш.А. и др. Алгебра. Учебник для 8 класса общеобразовательных учреждений. М., «Просвещение», 2008.).
Для учителя:
Коваленко В.Г., Дидактические игры на уроках математики. Книга для учителя. М.: «Просвещение», 1990
Макарова Л.В. Математические диктанты в VII-VIII классах «Математика в школе»,1999. №3,с.27
Буланова Л. М., Дудницын Ю. П. Проверочные задания по математике для учащихся 5-8 и 10 классов. – М.: Просвещение, 1998.
Жохов В. И., Макарычкв Ю. Н., Миндюк Н. Г. Дидактические материалы по алгебре,8 класс. – М.: Просвещение, 2000
Денищева Л.О и др. Зачёты в системе дифференцированного обучения математике.- М.: Просвещение, 1993.
Выгодский М.Я. Справочник по элементарной математике — М.: ООО «Издательство Астрель»: ООО «Издательство АСТ», 2003.
Никольский С.Н. Математика: Школьная энциклопедия — М.: Большая Российская энциклопедия; Дрофа, 1997.
Список дополнительной литературы по вопросам комбинаторики и теории вероятностей.
Бунимович Е. А., Булычев В. А. Основы статистики и вероятность. — М., 2004.
Виленкин Н. Я. Комбинаторика. — М., 1969.
Гмурман В. Е. Теория вероятностей и математическая статистика. — М., 1997.
Гнеденко Б. В., Хинчин А. Я. Элементарное введение в теорию вероятностей. М., 1982.
Лютикас B. C. Факультативный курс по математике. Теория вероятностей. — М., 1990. 7. Мостеллер Ф. Пятьдесят занимательных вероятностных задач с решениями. М., 1985.
Плоцки А. Вероятность в задачах для школьников. — М., 1996.
Ткачева М. В., Федорова Н. Е. Элементы статистики и вероятность. Учебное пособие для учащихся 7—9 кл. — М., 2005.
Тюрин Ю. Н. и др. Теория вероятностей и статистика. — М., 2004.
Для поддержки учебного процесса предполагается использование следующих информационных средств:
Министерство образования РФ: http://www.ed.gov.ru/ ; http://www.edu.ru
Тестирование online: 5 - 11 классы: http://www.kokch.kts.ru/cdo
Педагогическая Сеть «Методисты.ру» Математика в школе
Новые технологии в образовании: http://edu.secna.ru/main
Путеводитель «В мире науки» для школьников: http://www.uic.ssu.samara.ru
Мегаэнциклопедия Кирилла и Мефодия: http://mega.km.ru
сайты «Энциклопедий»: http://www.rubricon.ru/; http://www.encyclopedia.ru
сайт для самообразования и он-лайн тестирования: http://uztest.ru/
досье школьного учителя математики: http://www.mathvaz.ru/
Сайт учителя математики Шапошникова И.М.
Оглавление
Пояснительная записка к рабочей программе по предмету «АЛГЕБРА» в 9 классе
Цели и задачи
Требования к уровню подготовки учащихся
Технологии обучения и формы уроков
Место учебного предмета «АЛГЕБРА» в учебном плане школы
Содержание программы по разделам с указанием контрольных и самостоятельных работ, презентаций с применением ИКТ, количества часов по разделам
Тематическое планирование.
Формы и средства контроля.
Перечень учебно-методических средств обучения
ПРИЛОЖЕНИЯ
Поурочное планирование
Применение тестов и контрольных работ по предмету «АЛГЕБРА»
Формы периодического контроля знаний
Нормы оценки знаний
Пояснительная записка
Рабочая программа по курсу «АЛГЕБРА» составлена на основе федерального компонента государственного стандарта среднего (полного) общего образования приказом МО РФ № 1312 от 09.03.2004 г.
Нормативная основа программы
Закон РФ «Об образовании в РФ» от 4 января 2013 г.
Приказ Министерства образования и науки Российской Федерации от 17 декабря 2010 г. N 1897 "Об утверждении федерального государственного образовательного стандарта основного общего образования»,
«Требования к структуре основной образовательной программы основного общего образования» ФГОС основного общего образования, раздел III, пункт 18.2.2 Приказа Министерства образования и науки от 17.12.2012 № 1897,
Приказ Министерства образования и науки Российской Федерации от 17 мая 2012 года № 413 «Об утверждении федерального государственного образовательного стандарта среднего (полного) общего образования».
Учебный план ГБОУ школа № на учебный год.
Образовательная программа ГБОУ школа №
Цели и задачи
Школьное математическое образование ставит следующие цели обучения:
овладение конкретными математическими знаниями, необходимыми для применения в практической деятельности, для изучения смежных дисциплин, для продолжения образования;
интеллектуальное развитие учащихся, формирование качеств мышления, характерных для математической деятельности и необходимых для повседневной жизни;
формирование представлений об идеях и методах математики, о математике как форме описания и методе познания действительности;
формирование представлений о математике как части общечеловеческой культуры, понимания значимости математики для общественного прогресса.
При этом решаются следующие задачи:
развитие представление о числе, роли вычислений в человеческой практике; формирование практических навыков выполнения устных, письменных, инструментальных вычислений, развитие вычислительной культуры;
овладение символическим языком алгебры, выработка формально-оперативные алгебраических умений и применение их к решению математических и нематематических задач;
изучение свойств и графиков элементарных функций, научиться использовать функционально-графические представления для описания и анализа реальных зависимостей;
развитие пространственных представлений и изобразительных умений, освоение основных фактов и методов планиметрии, знакомство с простейшими пространственными телами и их свойствами;
получение представления о закономерностях в реальном мире и о различных способах их изучения.
развитие логического мышления и речи – умения логически обосновывать суждения, проводить несложные систематизации, приводить примеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства;
Требования к уровню подготовки учащихся
В рабочей программе представлено тематическое содержание курса алгебры для 8 класса по учебнику Алимова Ш.А.(, Алимов Ш.А. и др. Алгебра. Учебник для 9 класса общеобразовательных учреждений. М., «Просвещение», 2007.).
Уровень предварительной подготовки обучающегося для прохождения курса алгебра в 9 классе соответствует знаниям курсов алгебры 7 и 8 классов. Ученик должен знать и уметь:
Числовые и алгебраические дроби. Приведение подобных членов. Умножение многочленов. Разложение многочленов на простые множители. Решение линейных уравнений. Решение систем двух линейных уравнений. Графики линейных функций. 3 часа.
Виды неравенств. Действия с неравенствами. Решение неравенств. Неравенства с модулем. Решение систем неравенств с одной переменной.
Типы текстовых задач и способы их решения.
Смысл квадратного корня из числа. Свойства арифметического корня. Степени и корни числа и действия с ними.
Виды квадратных уравнений. Корни квадратного уравнения . Вывод формулы корней квадратного уравнения. Теорема Виета. Решение текстовых задач на составления квадратного уравнения.
Методы решения систем уравнений: подстановка, замена переменных, графический метод.
Определение квадратичной функции и ее свойства. Варианты квадратичных функций. Построение графиков.
Решение квадратичных неравенств. Метод разложения на множители. Метод интервалов.
В РЕЗУЛЬТАТЕ ОБУЧЕНИЯ УЧЕНИК ДОЛЖЕН:
уметь
составлять квадратные уравнения по условиям текстовых задач;
осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, выражать из формул одну переменную через другую;
выполнять основные действия со степенями с рациональными показателями; с многочленами; выполнять разложение многочленов на множители; выполнять тождественные преобразования целых выражений;
решать линейные и нелинейные уравнения, системы двух уравнений;
решать задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;;
находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;
строить графики изученных функций;
находить значение тригонометрической функции для острых и тупых углов;
использовать приобретенные знания и умения в практической деятельности для:
выполнения расчетов по формулам, для составления формул, выражающих зависимости между реальными величинами; для нахождения нужной формулы в справочных материалах;
моделирования практических ситуаций с использованием аппарата алгебры;
интерпретации графиков реальных зависимостей между величинами;
Технология обучения и формы уроков
Система уроков условна, но все же выделяются следующие виды:
Урок-лекция. Предполагаются совместные усилия учителя и учеников для решения общей проблемной познавательной задачи. На таком уроке используется демонстрационный материал на компьютере, разработанный учителем или учениками, мультимедийные продукты.
Урок-практикум. На уроке учащиеся работают над различными заданиями в зависимости от своей подготовленности. Виды работ могут быть самыми разными: письменные исследования, решение различных задач, изучение свойств различных функций, практическое применение различных методов решения задач. Компьютер на таких уроках используется как электронный калькулятор, тренажер устного счета, виртуальная лаборатория, источник справочной информации.
Урок-исследование. На уроке учащиеся решают проблемную задачу исследовательского характера аналитическим методом и с помощью компьютера с использованием различных лабораторий.
Комбинированный урок предполагает выполнение работ и заданий разного вида.
Урок решения задач. Вырабатываются у учащихся умения и навыки решения задач на уровне обязательной и возможной подготовке.
Урок-тест. Тестирование проводится с целью диагностики пробелов знаний, контроля уровня усвоения материала учащимися, тренировки технике тестирования. Тесты предлагаются как в печатном, так и в компьютерном варианте.
Урок-зачет. Устный опрос учащихся по заранее составленным вопросам, а также решение задач разного уровня по изученной теме.
Урок-самостоятельная работа. Предлагаются виды разноуровневых самостоятельных работ.
Урок-контрольная работа. Проводится на двух уровнях:
уровень обязательной подготовки - «3», уровень возможной подготовки - «4» и «5».
Компьютерное обеспечение уроков.
В разделе рабочей программы «Компьютерное обеспечение» спланировано применение имеющихся компьютерных продуктов: демонстрационный материал, задания для устного опроса учащихся, тренировочные упражнения, а также различные электронные учебники.
Демонстрационный материал (слайды).
Создается с целью обеспечения наглядности при изучении нового материала, использования при ответах учащихся. Изучение многих тем в математике связано с знанием и пониманием свойств элементарных функций. Решение уравнений, неравенств, различных задач предполагает глубокое знание поведения элементарных функций. Научиться распознавать графики таких функций, суметь рассказать об их свойствах помогают компьютерные слайды .
При решении любых задач использование графической интерпретации условия задачи, ее решения позволяет учащимся понять математическую идею решения, более глубоко осмыслить теоретический материал по данной теме.
Задания для устного счета.
Эти задания дают возможность в устном варианте отрабатывать различные вопросы теории и практики, применяя принципы наглядности, доступности. Их можно использовать на любом уроке в режиме учитель – ученик, взаимопроверки, а также в виде тренировочных занятий.
Электронные учебники (СД- и ДВД-диски)
Э.у. используются при проведении практических занятий, уроков введения новых знаний. В них заключен большой теоретический материал, практических и исследовательских заданий, справочного материала. На уроках возможно использование компьютерных устных упражнений, применение тренажера устного счета.
Использование компьютерных технологий в преподавании математики позволяет непрерывно менять формы работы на уроке, постоянно чередовать устные и письменные упражнения, осуществлять разные подходы к решению математических задач, а это постоянно создает и поддерживает интеллектуальное напряжение учащихся, формирует у них устойчивый интерес к изучению данного предмета.
Место предмета «АЛГЕБРА» в учебном плане школы
Согласно школьному базисному учебному плану для изучения алгебры в 9 классе отводится не менее 68 часов из расчета 2 часов в неделю для отд. НИИФ. Независимо от профильной направленности школы и класса алгебра является обязательным предметом, в виду необходимости сдавать экзамен за 9, а затем и 11 классы.
Содержание программы по разделам с указанием контрольных и самостоятельных работ, количества часов, средств ИКТ
Повторение основных разделов алгебры 7 и 8 класса. Действия с алгебраическими дробями. Линейные и квадратные уравнения. Линейные и квадратичные функции. Решение неравенств. 4 часа. 1 С.р. ИКТ
Алгебраические уравнения. Деление многочленов. Решение нелинейных уравнений и неравенств. Решение систем нелинейных уравнений. Решение текстовых задач на составление уравнений второй степени. 11 часов. 1 С.р., 1 К.р., ИКТ
Степень с рациональным показателем. Степень с целым показателем. Алгебраический корень и его свойства. Степень с рациональным показателем. Возведение в степень числовых неравенств. 7 часов. 1 С.р., 1 К.р., ИКТ
Степенная функция. Область определения функции. Возрастание и убывание функции. Четность и нечетность функций. Гиперболическая функция и ее свойства. Уравнения и неравенства, содержащие степень. 7 часов, 1 С.р., 1 К.р., ИКТ
Элементы тригонометрии. Градусная и радианная мера угла. Поворот точки на круговой диаграмме. Тригонометрические функции: синус, косинус, тангенс, котангенс и их определение. Значение тригонометрических функций для углов 30, 45, 60 градусов. Четность нечетность тригонометрических функций. Формулы суммы и разности. Формулы двойного аргумента. Формулы приведения и их назначение. 12 часов, 3 С.р., 1 К.р., ИКТ
Прогрессии. Числовые последовательности и их примеры. Арифметическая прогрессия и ее свойства. Сумма арифметической прогрессии. Геометрическая прогрессия и ее свойства. Сумма геометрической прогрессии. Убывающая геометрическая прогрессия. 11 часов, 1 С.р., 1 К.р., ИКТ
Подготовка к ГИА. Решение примеров и задач по курсам алгебра за 7 – 9 классы. Решение тестов. 14 часов. Итоговая контрольная работа. ИКТ
Тематическое планирование по алгебре в 9 классе.
Учебник «Алгебра-9» Алимов Ш.А., Колягин Ю.М. и др.,
Занятия 2 часа в неделю.
| № урока
| Тема урока
| № недели |
|
|
Тема 1. Повторение алгебры 7-8 классов. 4 часа |
|
| 1 | Алгебраические дроби Арифметический квадратный корень | 1 |
| 2 | Линейные уравнения, системы уравнений... | 1 |
| 3 | Линейные и квадратичные функции. | 2 |
| 4 | Неравенства, системы неравенств. Самостоятельная работа | 2 |
|
| Тема 2. Алгебраические уравнения. 11 часов |
|
| 5 | Деление многочленов. | 3 |
| 6--7 | Решение алгебраических уравнений. Самостоятельная работа | 3 и 4 |
| 8 | Уравнения, сводящиеся к алгебраическим. | 4 |
| 9-10 | Системы нелинейных уравнений с двумя неизвестными. | 5 |
| 11-12 | Различные способы решения систем уравнений. | 6 |
| 13-14 | Решение задач с помощью систем уравнений. | 7 |
| 15 | Контрольная работа №1 | 8 |
|
| Тема 3 Степень с рациональным показателем. 7 часов |
|
| 16 | Степень с целым показателем. | 8 |
| 17 | Арифметический корень натуральной степени. | 9 |
| 18 | Свойства арифметического корня. Самостоятельная работа | 9 |
| 19 | Степень с рациональным показателем. | 10 |
| 20 | Возведение в степень числового неравенства. | 10 |
| 21 | Решение примеров на степени и корни. | 11 |
| 22 | Контрольная работа № 2. | 11 |
|
| Тема 4 Степенная функция. 7 часов |
|
| 23 | Область определения функции. | 12 |
| 24 | Возрастание и убывание функции. | 12 |
| 25 | Чётность и нечётность функции. Самостоятельная работа. | 13 |
| 26 | Функция y=k/x | 13 |
| 27 | Неравенства и уравнения, содержащие степень. | 14 |
| 28 | Решение примеров по теме. | 14 |
| 29 | Контрольная работа № 3. | 15 |
|
| Тема 5 Элементы тригонометрии. 12 часов |
|
| 30 | Радианная мера угла. | 15 |
| 31 | Поворот точки вокруг начала координат. | 16 |
| 32 | Определение синуса, косинуса и тангенса угла. | 16 |
| 33 | Знаки синуса, косинуса и тангенса в координатных четвертях. Самостоятельная работа
| 17 |
| 34 | Зависимость между синусом, косинусом и тангенсом одного и того же угла. Самостоятельная работа. | 17 |
| 35 | Тригонометрические тождества | 18 |
| 36 | Четность и нечетность функций | 18 |
| 37 | Формулы сложения. Самостоятельная работа | 19 |
| 38 | Формулы двойного угла | 19 |
| 39 | Формулы приведения | 20 |
| 40 | Решение примеров по теме | 20 |
| 41 | Контрольная работа № 4 | 21 |
|
| Тема 6. Прогрессии. 11 часов |
|
| 42 | Числовая последовательность. | 21 |
| 43 | Арифметическая прогрессия. | 22 |
| 44-45 | Сумма n первых членов арифметической прогрессии. Самостоятельная работа | 22 и 23 |
| 46 | Геометрическая прогрессия. | 23 |
| 47-48 | Сумма n первых членов геометрической прогрессии. | 24 |
| 49 | Бесконечно убывающая геометрическая прогрессия. | 25 |
| 50-51 | Решение примеров по теме. | 25 и 26 |
| 52 | Контрольная работа № 5 по данной теме | 26 |
| 53-67 | ПОДГОТОВКА К ГИА. Решение примеров и задач по курсам алгебра 7 – 9 классов. 14 часов | 27-34 |
| 68 | Итоговая контрольная работа. | 34 |
Самостоятельных работ - 8
Контрольных работ - 6
Формы и средства контроля.
Основными методами проверки знаний и умений учащихся по алгебре являются устный опрос, письменные работы. К письменным формам контроля относятся: математические диктанты, самостоятельные и контрольные работы, тесты. Основные виды проверки знаний – текущая и итоговая. Текущая проверка проводится систематически из урока в урок, а итоговая – по завершении темы (раздела), школьного курса. Варианты проверочных работ по каждой теме был приведен выше.
Типы индивидуальных консультаций и прием зачетов в отд. НИИФ
Выявление и ликвидация пробелов в знаниях обучающихся
Подготовка к изучению нового материала
Решение задач практического содержания и задач повышенной трудности
Подготовка к контрольной работе
Формы и методы проведения зачета:
Устно-индивидуальный опрос по карточкам-заданиям
Тест
Групповое собеседование
Письменный зачет
Устно-письменный зачет
Письменные ответы на вопросы
Перечень учебно-методических средств обучения
Для учащихся:
Алимов Ш.А. и др. Алгебра. Учебник для 8 класса общеобразовательных учреждений. М., «Просвещение», 2007.).
Для учителя:
Коваленко В.Г., Дидактические игры на уроках математики. Книга для учителя. М.: «Просвещение», 1990
Макарова Л.В. Математические диктанты в VII-VIII классах «Математика в школе»,1999. №3,с.27
Буланова Л. М., Дудницын Ю. П. Проверочные задания по математике для учащихся 5-8 и 10 классов. – М.: Просвещение, 1998.
Жохов В. И., Макарычкв Ю. Н., Миндюк Н. Г. Дидактические материалы по алгебре,8 класс. – М.: Просвещение, 2000
Денищева Л.О и др. Зачёты в системе дифференцированного обучения математике.- М.: Просвещение, 1993.
Выгодский М.Я. Справочник по элементарной математике — М.: ООО «Издательство Астрель»: ООО «Издательство АСТ», 2003.
Никольский С.Н. Математика: Школьная энциклопедия — М.: Большая Российская энциклопедия; Дрофа, 1997.
Для поддержки учебного процесса предполагается использование электронных носителей (СД_ и ДВД-диски) и интернет порталы.
Министерство образования РФ: http://www.ed.gov.ru/ ; http://www.edu.ru
Тестирование online: 5 - 11 классы: http://www.kokch.kts.ru/cdo
Педагогическая Сеть «Методисты.ру» Математика в школе
Новые технологии в образовании: http://edu.secna.ru/main
Путеводитель «В мире науки» для школьников: http://www.uic.ssu.samara.ru
Мегаэнциклопедия Кирилла и Мефодия: http://mega.km.ru
сайты «Энциклопедий»: http://www.rubricon.ru/; http://www.encyclopedia.ru
сайт для самообразования и он-лайн тестирования: http://uztest.ru/
досье школьного учителя математики: http://www.mathvaz.ru/
Сайт учителя математики Шапошникова И.М.
Оглавление
Пояснительная записка к рабочей программе по предмету «АЛГЕБРА» в10 классе
Цели и задачи
Требования к уровню подготовки учащихся
Технологии обучения и формы уроков
Место учебного предмета «АЛГЕБРА» в учебном плане школы
Содержание программы по разделам с указанием контрольных и самостоятельных работ, презентаций с применением ИКТ, количества часов по разделам
Тематическое планирование.
Формы и средства контроля.
Перечень учебно-методических средств обучения
ПРИЛОЖЕНИЯ
Поурочное планирование
Применение тестов и контрольных работ по предмету «АЛГЕБРА»
Формы периодического контроля знаний
Нормы оценки знаний
Пояснительная записка
Рабочая программа по курсу «АЛГЕБРА» составлена на основе федерального компонента государственного стандарта среднего (полного) общего образования приказом МО РФ № 1312 от 09.03.2004 г.
Нормативная основа программы
Закон РФ «Об образовании в РФ» от 4 января 2013 г.
Приказ Министерства образования и науки Российской Федерации от 17 декабря 2010 г. N 1897 "Об утверждении федерального государственного образовательного стандарта основного общего образования»,
«Требования к структуре основной образовательной программы основного общего образования» ФГОС основного общего образования, раздел III, пункт 18.2.2 Приказа Министерства образования и науки от 17.12.2012 № 1897,
Приказ Министерства образования и науки Российской Федерации от 17 мая 2012 года № 413 «Об утверждении федерального государственного образовательного стандарта среднего (полного) общего образования».
Закон РФ №3266-1 от 10.07.92 «Индивидуальное обучение детей»..
Учебный план ГБОУ школа №... на ____учебный год.
Образовательная программа ГБОУ школа №
Цели и задачи
Школьное математическое образование ставит следующие цели обучения:
овладение конкретными математическими знаниями, необходимыми для применения в практической деятельности, для изучения смежных дисциплин, для продолжения образования;
интеллектуальное развитие учащихся, формирование качеств мышления, характерных для математической деятельности и необходимых для повседневной жизни;
формирование представлений об идеях и методах математики, о математике как форме описания и методе познания действительности;
формирование представлений о математике как части общечеловеческой культуры, понимания значимости математики для общественного прогресса.
При этом решаются следующие задачи:
развитие представление о числе, роли вычислений в человеческой практике; формирование практических навыков выполнения устных, письменных, инструментальных вычислений, развитие вычислительной культуры;
овладение символическим языком алгебры, выработка формально-оперативные алгебраических умений и применение их к решению математических и нематематических задач;
изучение свойств и графиков элементарных функций, научиться использовать функционально-графические представления для описания и анализа реальных зависимостей;
развитие пространственных представлений и изобразительных умений, освоение основных фактов и методов планиметрии, знакомство с простейшими пространственными телами и их свойствами;
получение представления о закономерностях в реальном мире и о различных способах их изучения.
развитие логического мышления и речи – умения логически обосновывать суждения, проводить несложные систематизации, приводить примеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства;
Требования к уровню подготовки учащихся
В рабочей программе представлено тематическое содержание курса алгебры для 8 класса по учебнику Алимова Ш.А.(, Алимов Ш.А. и др. Алгебра. Учебник для 10-11 классов общеобразовательных учреждений. М., «Просвещение», 2007.).
Уровень предварительной подготовки обучающегося для прохождения курса алгебра в 10 классе соответствует знаниям курсов алгебры 7, 8 и 9 классов. Ученик должен знать и уметь:
Виды неравенств. Действия с неравенствами. Решение неравенств. Неравенства с модулем. Решение систем неравенств с одной переменной.
Типы текстовых задач и способы их решения.
Смысл квадратного корня из числа. Свойства арифметического корня. Степени и корни числа и действия с ними.
Виды квадратных уравнений. Корни квадратного уравнения . Вывод формулы корней квадратного уравнения. Теорема Виета. Решение текстовых задач на составления квадратного уравнения.
Методы решения систем уравнений: подстановка, замена переменных, графический метод.
Квадратичная функция и ее свойства. Варианты квадратичных функций. Построение графиков.
Решение квадратичных неравенств. Метод разложения на множители. Метод интервалов. Степень с рациональным показателем. Построение графиков некоторых степенных функций.
Элементы тригонометрии. Связь между тригонометрическими функциями. Основные тригонометрические тождества. Формулы сложения и двойного угла. Формулы приведения и их назначение.
В РЕЗУЛЬТАТЕ ОБУЧЕНИЯ УЧЕНИК ДОЛЖЕН:
уметь
составлять квадратные уравнения по условиям текстовых задач;
осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, выражать из формул одну переменную через другую;
выполнять основные действия со степенями с рациональными показателями; с многочленами; выполнять разложение многочленов на множители; выполнять тождественные преобразования целых выражений;
решать линейные и нелинейные уравнения, системы двух уравнений;
решать задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;;
находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;
строить графики изученных функций;
находить значение тригонометрической функции для острых и тупых углов;
использовать приобретенные знания и умения в практической деятельности для:
выполнения расчетов по формулам, для составления формул, выражающих зависимости между реальными величинами; для нахождения нужной формулы в справочных материалах;
моделирования практических ситуаций с использованием аппарата алгебры;
интерпретации графиков реальных зависимостей между величинами;
Технология обучения и формы уроков
Система уроков условна, но все же выделяются следующие виды:
Урок-лекция. Предполагаются совместные усилия учителя и учеников для решения общей проблемной познавательной задачи. На таком уроке используется демонстрационный материал на компьютере, разработанный учителем или учениками, мультимедийные продукты.
Урок-практикум. На уроке учащиеся работают над различными заданиями в зависимости от своей подготовленности. Виды работ могут быть самыми разными: письменные исследования, решение различных задач, изучение свойств различных функций, практическое применение различных методов решения задач. Компьютер на таких уроках используется как электронный калькулятор, тренажер устного счета, виртуальная лаборатория, источник справочной информации.
Урок-исследование. На уроке учащиеся решают проблемную задачу исследовательского характера аналитическим методом и с помощью компьютера с использованием различных лабораторий.
Комбинированный урок предполагает выполнение работ и заданий разного вида.
Урок решения задач. Вырабатываются у учащихся умения и навыки решения задач на уровне обязательной и возможной подготовке.
Урок-тест. Тестирование проводится с целью диагностики пробелов знаний, контроля уровня усвоения материала учащимися, тренировки технике тестирования. Тесты предлагаются как в печатном, так и в компьютерном варианте.
Урок-зачет. Устный опрос учащихся по заранее составленным вопросам, а также решение задач разного уровня по изученной теме.
Урок-самостоятельная работа. Предлагаются виды разноуровневых самостоятельных работ.
Урок-контрольная работа. Проводится на двух уровнях:
уровень обязательной подготовки - «3», уровень возможной подготовки - «4» и «5».
Компьютерное обеспечение уроков.
В разделе рабочей программы «Компьютерное обеспечение» спланировано применение имеющихся компьютерных продуктов: демонстрационный материал, задания для устного опроса учащихся, тренировочные упражнения, а также различные электронные учебники.
Демонстрационный материал (слайды).
Создается с целью обеспечения наглядности при изучении нового материала, использования при ответах учащихся. Изучение многих тем в математике связано с знанием и пониманием свойств элементарных функций. Решение уравнений, неравенств, различных задач предполагает глубокое знание поведения элементарных функций. Научиться распознавать графики таких функций, суметь рассказать об их свойствах помогают компьютерные слайды .
При решении любых задач использование графической интерпретации условия задачи, ее решения позволяет учащимся понять математическую идею решения, более глубоко осмыслить теоретический материал по данной теме.
Задания для устного счета.
Эти задания дают возможность в устном варианте отрабатывать различные вопросы теории и практики, применяя принципы наглядности, доступности. Их можно использовать на любом уроке в режиме учитель – ученик, взаимопроверки, а также в виде тренировочных занятий.
Электронные учебники (СД_ и ДВД-диски)
Э.у. используются при проведении практических занятий, уроков введения новых знаний. В них заключен большой теоретический материал, практических и исследовательских заданий, справочного материала. На уроках возможно использование компьютерных устных упражнений, применение тренажера устного счета.
Использование компьютерных технологий в преподавании математики позволяет непрерывно менять формы работы на уроке, постоянно чередовать устные и письменные упражнения, осуществлять разные подходы к решению математических задач, а это постоянно создает и поддерживает интеллектуальное напряжение учащихся, формирует у них устойчивый интерес к изучению данного предмета.
Место предмета «АЛГЕБРА» в учебном плане школы
Согласно школьному базисному учебному плану для изучения алгебры в 9 классе отводится не менее 68 часов из расчета 2 часов в неделю для отд. НИИФ. Независимо от профильной направленности школы и класса алгебра является обязательным предметом, в виду необходимости сдавать экзамен за 9, а затем и 11 классы.
Содержание программы по разделам курса алгебры 10 класса (Учебник Алгебра 10 – 11 классов, авт. Алимов Ш.А., Колягин Ю.М. и др., )
Занятия 2 часа в неделю.
Повторение 3 часа
Числовые множества. Рациональные и иррациональные числа. Последовательности. Арифметическая и геометрическая прогрессии. Числа в рациональной степени. Арифметический корень числа.
Дробно-рациональные и дробно-иррациональные выражения. 3 часа, 1 К.р.
Решение дробно-рациональных и дробно-иррациональных уравнений. Взаимообратные функции и их свойства. Графики обратных функций.
Степенные функции 2 часа
четной и нечетной степени. Графики степенных функций с целой, дробной, положительной и отрицательной степенью.
Показательные функции. 5 часов 1 С.р., 1 К.р.
Свойства показательных функций. Графики показательных функций. Решение показательных уравнений и неравенств. Системы показательных уравнений и неравенств.
Логарифмические функции. 7 часов, 1 С.р., 1 К.р.
Определение и свойства логарифмической функции. Графики логарифмических функций. Формулы для преобразования логарифмических выражений. Решение логарифмических уравнений и неравенств. Решение систем логарифмических уравнений и неравенств.
Тригонометрические функции. 18 часов, 4 С.р., 1 К.р.
Области существования и значения тригонометрических функций. Тригонометрические тождества. Четность и нечетность тригонометрических функций. Периодичность тригонометрических функций. Графики тригонометрических функций. Формулы приведение и их назначение. Формулы тригонометрических функций суммы двух углов. Формулы двойного угла. Формулы понижения степени тригонометрической функции. Формулы суммы и разности двух тригонометрических функций. Формулы произведения двух тригонометрических функций.
Тригонометрические уравнения. 7 часов, 3 С.р., 1 К.р.
Обратные тригонометрические функции. Преобразование тригонометрических выражений. Решение тригонометрических уравнений. Методы решения тригонометрических уравнений. Решение тригонометрических неравенств.
Предел функции . 2 часа, 1 С.р.
Его иллюстрация на отдельных примерах. Определение.
Производная. 8 часов, 1 С.р., 1 К.р.
Ее связь с пределом функции. Геометрический и физический смысл производной. Таблица правил дифференцирования для элементарных функций. Решение примеров на дифференцирование алгебраических функций.
Исследование алгебраических функций. 14 часов, 3 С.р., 1 К.р.
Области существования и значения функций. Четность и нечетность. Области возрастания и убывания функции. Периодичность функции. Нахождение экстремумов функции и точек перегибов. Особые точки функции. Построение эскизов графиков функций после их исследования.
Повторение некоторых тем. 6 часов, 1 К.р.
Решение иррациональных и тригонометрических уравнений. Решение показательных и логарифмических уравнений. Исследование и построение графиков.
Тематическое планирование курса алгебры 10 класса Учебник «Алгебра-10-11» Алимов Ш.А., Колягин Ю.М. и др.,
2 часа в неделю(68 часов в год)
| № урока | ТЕМЫ | контроль | № недели |
|
| Тема 1 Повторение 3 часа |
|
|
| 1 | Числовые множества: натуральные, целые, рациональные, иррациональные, комплексные числа |
| 1 |
| 2 | Последовательности. Арифметическая и геометрическая прогрессии. Сумма n – членов прогрессии. |
| 1 |
| 3 | Степень числа. Арифметический корень числа. |
| 1 |
|
| Тема 2 Дробно-рациональные и дробно-иррациональные выражения 3 часа |
|
|
| 4 | Решение дробно-рациональных и дробно-иррациональных уравнений |
| 2 |
| 5 | Взаимообратные функции и их свойства. |
| 3 |
| 6 | Контрольная работа №1 | К.р. | 3 |
|
| Тема 3 Степенные функции 2 часа |
|
|
| 7-8 | Свойства и графики степенных функций с целыми, дробными, четными и нечетными показателями степени. |
| 4 |
|
| Тема 4 Показательные функции.5 часов |
|
|
| 9 | Свойства и графики показательных функций. |
| 5 |
| 10-11 | Решение показательных уравнений и неравенств. Самостоятельная работа. | С.р. | 5 и 6 |
| 12 | Решение систем из двух показательных уравнений или двух неравенств. |
| 6 |
| 13 | Контрольная работа №2 | К.р. | 7 |
|
| Тема 5Логарифмические функции 7 часов |
|
|
| 14 | Определение и свойства логарифмической функции. |
| 7 |
| 15 | Графики возрастающей и убывающей логарифмических функций. |
| 7 |
| 16 | Формулы для преобразования логарифмических выражений. Самостоятельная работа. | С.р. | 8 |
| 17 | Решение логарифмических уравнений и неравенств. |
| 8 и 9 |
| 18-19 | Решение систем логарифмических уравнений и неравенств. |
| 9 |
| 20 | Контрольная работа №3 | К.р. | 10 |
|
| Тема 6Тригонометрические функции 18 часа |
|
|
| 21 | Градусная и радианная мера угла и их взаимосвязь. |
| 10 |
| 22 | Определение тригонометрических функций. Их области существования и области значений. |
| 10 и 11 |
| 23 | Тригонометрические тождества. |
| 11 |
| 24-25 | Взаимосвязь тригонометрических функций через тождества. Самостоятельная работа. | С.р. | 11 и 12 |
| 26 | Четность и нечетность. Периодичность тригонометрических функций. |
| 12 |
| 27 | Графики тригонометрических функций. |
| 13 |
| 28-29 | Формулы приведения и их назначение. Решение примеров. Самостоятельная работа. | С.р. | 13 и 14 |
| 30 | Формулы тригонометрических функций суммы и разности двух углов. Решение примеров |
| 14 |
| 31-32 | Формулы двойного угла. Формулы понижения степени функции. Самостоятельная работа. | С.р. | 15 |
| 33 | Формулы суммы и разности двух функций с разными углами. Решение примеров |
| 15 и16 |
| 34-35 | Формулы произведений двух тригонометрических функций с разными углами. Самостоятельная работа. | С.р. | 16 |
| 36-37 | Решение примеров на преобразования тригонометрических выражений и доказательства тождеств. |
| 17 |
| 38 | Контрольная работа №4 | К.р. | 18 |
|
| Тема 7 Тригонометрические уравнения 7 часов |
|
|
| 39 | Простейшие тригонометрические уравнения и формулы для их решений. |
| 18 |
| 40 | Обратные тригонометрические функции и их свойства. Решение примеров. |
| 19 |
| 41 | Преобразования тригонометрических уравнений и разложение их на множители. Решение примеров. Самостоятельная работа. | С.р. | 20 и 21 |
| 42 | Методы решения тригонометрических уравнений. Решение примеров Самостоятельная работа | С.р. | 21 и 22 |
| 43-44 | Тригонометрические неравенства и их решение. Решение примеров. |
| 23 |
| 45 | Контрольная работа №5 | К.р. | 24 |
|
| Тема 8 Пределы 2часа |
|
|
| 46 | Определение предела последовательности и функции. |
| 24 |
| 47 | Назначение пределов. Примеры, связанные с определением пределов. Самостоятельная работа. | С.р. | 24 и 25 |
|
| Тема 9 Производная 8 часов |
|
|
| 48 | Понятие производной и ее связь с пределом функции. |
| 25 |
| 49 | Определение производной. Нахождение производной для простых функций типа х2 , х3 |
| 25 и 26 |
| 50 | Геометрический и физический смысл производной |
| 26 |
| 51-52 | Таблица правил дифференцирования (взятие производной) элементарных функций. Самостоятельная работа. | С.р. | 26 и 27 |
| 53 | Решение примеров на дифференцирование функций. |
| 27 |
| 54 | Контрольная работа №6 | К.р. | 28 |
|
| Тема10 Исследование алгебраических функций 14 часов |
|
|
| 55 | Области существования и значений функции. Решение примеров. Самостоятельная работа. | С.р. | 28 |
| 56 | Четность и нечетность функций. |
| 29 |
| 57 | Периодичность функций. Самостоятельная работа. | С.р. | 29 |
| 58 | Применение производной при исследовании функции. Нахождение экстремумов функций, точек перегибов. |
| 29 |
| 59 | Нахождение интервалов монотонности: возрастания и убывания функции. Решение примеров. Самостоятельная работа. | С.р. | 30 |
| 60 | Особые точки и значение функции в этих точках. Решение примеров. |
| 31 |
| 61-62 | Построение эскизов графиков функций после их исследования. Решение примеров. Самостоятельная работа. |
| 31 и 32 |
| 63 | Контрольная работа №7 | К.р. | 32 |
|
| Тема 11 Повторение некоторых тем 6 часов |
|
|
| 64 | Решение иррациональных уравнений |
| 33 |
| 65 | Решение показательных и логарифмических уравнений. |
| 33 |
| 66 | Решение тригонометрических уравнений |
| 33 |
| 67 | Исследование функций и построение графиков. |
| 34 |
| 68 | Итоговая контрольная работа | К.р. | 34 |
|
|
|
|
|
Самостоятельных работ – 13, Контрольных работ - 8
Формы и средства контроля.Основными методами проверки знаний и умений учащихся по алгебре являются устный опрос, письменные работы. К письменным формам контроля относятся: математические диктанты, самостоятельные и контрольные работы, тесты. Основные виды проверки знаний – текущая и итоговая. Текущая проверка проводится систематически из урока в урок, а итоговая – по завершении темы (раздела), школьного курса.
Типы индивидуальных консультаций и прием зачетов в отд. НИИФ
Выявление и ликвидация пробелов в знаниях обучающихся
Подготовка к изучению нового материала
Решение задач практического содержания и задач повышенной трудности
Подготовка к контрольной работе
Формы и методы проведения зачета:
Устно-индивидуальный опрос по карточкам-заданиям
Тест
Групповое собеседование
Письменный зачет
Устно-письменный зачет
Письменные ответы на вопросы
Перечень учебно-методических средств обучения
Для учащихся:
Алимов Ш.А. и др. Алгебра, Учебник для 10-11 классов общеобразовательных учреждений. М., «Просвещение», 2007.).
Для учителя:
Коваленко В.Г., Дидактические игры на уроках математики. Книга для учителя. М.: «Просвещение», 1990
Макарова Л.В. Математические диктанты в VII-VIII классах «Математика в школе»,1999. №3,с.27
Буланова Л. М., Дудницын Ю. П. Проверочные задания по математике для учащихся 5-8 и 10 классов. – М.: Просвещение, 1998.
Жохов В. И., Макарычкв Ю. Н., Миндюк Н. Г. Дидактические материалы по алгебре,8 класс. – М.: Просвещение, 2000
Денищева Л.О и др. Зачёты в системе дифференцированного обучения математике.- М.: Просвещение, 1993.
Выгодский М.Я. Справочник по элементарной математике — М.: ООО «Издательство Астрель»: ООО «Издательство АСТ», 2003.
Никольский С.Н. Математика: Школьная энциклопедия — М.: Большая Российская энциклопедия; Дрофа, 1997.
Для поддержки учебного процесса предполагается использование Интернет ресурсы и электронные носители информации (СД- и ДВД-диски)
.Образовательная коллекция 1С: Алгебра 7-11класс
Министерство образования РФ: http://www.ed.gov.ru/ ; http://www.edu.ru
Тестирование online: 5 - 11 классы: http://www.kokch.kts.ru/cdo
Педагогическая Сеть «Методисты.ру» Математика в школе
Новые технологии в образовании: http://edu.secna.ru/main
Путеводитель «В мире науки» для школьников: http://www.uic.ssu.samara.ru
Мегаэнциклопедия Кирилла и Мефодия: http://mega.km.ru
сайты «Энциклопедий»: http://www.rubricon.ru/; http://www.encyclopedia.ru
сайт для самообразования и он-лайн тестирования: http://uztest.ru/
досье школьного учителя математики: http://www.mathvaz.ru/
Сайт учителя математики Шапошникова И.М.
Оглавление
Пояснительная записка к рабочей программе по предмету «АЛГЕБРА» в11 классе
Цели и задачи
Требования к уровню подготовки учащихся
Технологии обучения и формы уроков
Место учебного предмета «АЛГЕБРА» в учебном плане школы
Содержание программы по разделам с указанием контрольных и самостоятельных работ, презентаций с применением ИКТ, количества часов по разделам
Тематическое планирование.
Формы и средства контроля.
Перечень учебно-методических средств обучения
ПРИЛОЖЕНИЯ
Поурочное планирование
Применение тестов и контрольных работ по предмету «АЛГЕБРА»
Формы периодического контроля знаний
Нормы оценки знаний
Пояснительная записка
Рабочая программа по курсу «АЛГЕБРА» составлена на основе федерального компонента государственного стандарта среднего (полного) общего образования приказом МО РФ № 1312 от 09.03.2004 г.
Нормативная основа программы
Закон РФ «Об образовании в РФ» от 4 января 2013 г.
Приказ Министерства образования и науки Российской Федерации от 17 декабря 2010 г. N 1897 "Об утверждении федерального государственного образовательного стандарта основного общего образования»,
«Требования к структуре основной образовательной программы основного общего образования» ФГОС основного общего образования, раздел III, пункт 18.2.2 Приказа Министерства образования и науки от 17.12.2012 № 1897,
Приказ Министерства образования и науки Российской Федерации от 17 мая 2012 года № 413 «Об утверждении федерального государственного образовательного стандарта среднего (полного) общего образования».
Закон РФ №3266-1 от 10.07.92 «Индивидуальное обучение детей»..
Учебный план ГБОУ школа № 517 ... на _____ учебный год.
Образовательная программа ГБОУ школа №..
Цели и задачи
Школьное математическое образование ставит следующие цели обучения:
овладение конкретными математическими знаниями, необходимыми для применения в практической деятельности, для изучения смежных дисциплин, для продолжения образования;
интеллектуальное развитие учащихся, формирование качеств мышления, характерных для математической деятельности и необходимых для повседневной жизни;
формирование представлений об идеях и методах математики, о математике как форме описания и методе познания действительности;
формирование представлений о математике как части общечеловеческой культуры, понимания значимости математики для общественного прогресса.
При этом решаются следующие задачи:
развитие представление о числе, роли вычислений в человеческой практике; формирование практических навыков выполнения устных, письменных, инструментальных вычислений, развитие вычислительной культуры;
овладение символическим языком алгебры, выработка формально-оперативные алгебраических умений и применение их к решению математических и нематематических задач;
изучение свойств и графиков элементарных функций, научиться использовать функционально-графические представления для описания и анализа реальных зависимостей;
развитие пространственных представлений и изобразительных умений, освоение основных фактов и методов планиметрии, знакомство с простейшими пространственными телами и их свойствами;
получение представления о закономерностях в реальном мире и о различных способах их изучения.
развитие логического мышления и речи – умения логически обосновывать суждения, проводить несложные систематизации, приводить примеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства;
Требования к уровню подготовки учащихся
В рабочей программе представлено тематическое содержание курса алгебры для 8 класса по учебнику Алимова Ш.А.(, Алимов Ш.А. и др. Алгебра. Учебник для 10-11 класса общеобразовательных учреждений. М., «Просвещение», 2007.).
Уровень предварительной подготовки обучающегося для прохождения курса алгебра в 11 классе соответствует знаниям курсов алгебры 7, 8, 9и 10 классов. Ученик должен знать и уметь:
Виды неравенств. Действия с неравенствами. Решение неравенств. Неравенства с модулем. Решение систем неравенств с одной переменной.
Типы текстовых задач и способы их решения.
Смысл квадратного корня из числа. Свойства арифметического корня. Степени и корни числа и действия с ними.
Виды квадратных уравнений. Корни квадратного уравнения . Вывод формулы корней квадратного уравнения. Теорема Виета. Решение текстовых задач на составления квадратного уравнения.
Методы решения систем уравнений: подстановка, замена переменных, графический метод.
Квадратичная функция и ее свойства. Варианты квадратичных функций. Построение графиков.
Решение квадратичных неравенств. Метод разложения на множители. Метод интервалов. Степень с рациональным показателем. Построение графиков некоторых степенных функций.
Элементы тригонометрии. Связь между тригонометрическими функциями. Основные тригонометрические тождества. Формулы сложения и двойного угла. Формулы приведения и их назначение.
Числовые множества. Рациональные и иррациональные числа. Последовательности. Арифметическая и геометрическая прогрессии. Числа в рациональной степени. Арифметический корень числа.
Степенные функции четной и нечетной степени. Графики степенных функций с целой, дробной, положительной и отрицательной степенью.
Решение дробно-рациональных и дробно-иррациональных уравнений. Взаимообратные функции и их свойства. Графики обратных функций.
Свойства показательных функций. Графики показательных функций. Решение показательных уравнений и неравенств. Системы показательных уравнений и неравенств.
Определение и свойства логарифмической функции. Графики логарифмических функций. Формулы для преобразования логарифмических выражений. Решение логарифмических уравнений и неравенств. Решение систем логарифмических уравнений и неравенств.
Области существования и значения тригонометрических функций. Тригонометрические тождества. Четность и нечетность тригонометрических функций. Периодичность тригонометрических функций. Графики тригонометрических функций. Формулы приведение и их назначение. Формулы тригонометрических функций суммы двух углов. Формулы двойного угла. Формулы понижения степени тригонометрической функции. Формулы суммы и разности двух тригонометрических функций. Формулы произведения двух тригонометрических функций.
Обратные тригонометрические функции. Преобразование тригонометрических выражений. Решение тригонометрических уравнений. Методы решения тригонометрических уравнений. Решение тригонометрических неравенств.
Предел функции и его иллюстрация на отдельных примерах. Определение.
Понятие производной и ее связь с пределом функции. Геометрический и физический смысл производной. Таблица правил дифференцирования для элементарных функций. Решение примеров на дифференцирование алгебраических функций.
Области существования и значения функций. Четность и нечетность. Области возрастания и убывания функции. Периодичность функции. Нахождение экстремумов функции и точек перегибов. Особые точки функции. Построение эскизов графиков функций после их исследования.
В РЕЗУЛЬТАТЕ ОБУЧЕНИЯ УЧЕНИК ДОЛЖЕН:
уметь
составлять квадратные уравнения по условиям текстовых задач;
осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, выражать из формул одну переменную через другую;
выполнять основные действия со степенями с рациональными показателями; с многочленами; выполнять разложение многочленов на множители; выполнять тождественные преобразования целых выражений;
решать линейные и нелинейные уравнения, системы двух уравнений;
решать задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;;
находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;
строить графики изученных функций, используя производные
находить значение тригонометрической функции для острых и тупых углов;
использовать приобретенные знания и умения в практической деятельности для:
выполнения расчетов по формулам, для составления формул, выражающих зависимости между реальными величинами; для нахождения нужной формулы в справочных материалах;
моделирования практических ситуаций с использованием аппарата алгебры;
интерпретации графиков реальных зависимостей между величинами;
Технология обучения и формы уроков
Система уроков условна, но все же выделяются следующие виды:
Урок-лекция. Предполагаются совместные усилия учителя и учеников для решения общей проблемной познавательной задачи. На таком уроке используется демонстрационный материал на компьютере, разработанный учителем или учениками, мультимедийные продукты.
Урок-практикум. На уроке учащиеся работают над различными заданиями в зависимости от своей подготовленности. Виды работ могут быть самыми разными: письменные исследования, решение различных задач, изучение свойств различных функций, практическое применение различных методов решения задач. Компьютер на таких уроках используется как электронный калькулятор, тренажер устного счета, виртуальная лаборатория, источник справочной информации.
Урок-исследование. На уроке учащиеся решают проблемную задачу исследовательского характера аналитическим методом и с помощью компьютера с использованием различных лабораторий.
Комбинированный урок предполагает выполнение работ и заданий разного вида.
Урок решения задач. Вырабатываются у учащихся умения и навыки решения задач на уровне обязательной и возможной подготовке.
Урок-тест. Тестирование проводится с целью диагностики пробелов знаний, контроля уровня усвоения материала учащимися, тренировки технике тестирования. Тесты предлагаются как в печатном, так и в компьютерном варианте.
Урок-зачет. Устный опрос учащихся по заранее составленным вопросам, а также решение задач разного уровня по изученной теме.
Урок-самостоятельная работа. Предлагаются виды разноуровневых самостоятельных работ.
Урок-контрольная работа. Проводится на двух уровнях:
уровень обязательной подготовки - «3», уровень возможной подготовки - «4» и «5».
Компьютерное обеспечение уроков.
В разделе рабочей программы «Компьютерное обеспечение» спланировано применение имеющихся компьютерных продуктов: демонстрационный материал, задания для устного опроса учащихся, тренировочные упражнения, а также различные электронные учебники.
Демонстрационный материал (слайды).
Создается с целью обеспечения наглядности при изучении нового материала, использования при ответах учащихся. Изучение многих тем в математике связано с знанием и пониманием свойств элементарных функций. Решение уравнений, неравенств, различных задач предполагает глубокое знание поведения элементарных функций. Научиться распознавать графики таких функций, суметь рассказать об их свойствах помогают компьютерные слайды .
При решении любых задач использование графической интерпретации условия задачи, ее решения позволяет учащимся понять математическую идею решения, более глубоко осмыслить теоретический материал по данной теме.
Задания для устного счета.
Эти задания дают возможность в устном варианте отрабатывать различные вопросы теории и практики, применяя принципы наглядности, доступности. Их можно использовать на любом уроке в режиме учитель – ученик, взаимопроверки, а также в виде тренировочных занятий.
Электронные учебники.
Э.у. используются при проведении практических занятий, уроков введения новых знаний. В них заключен большой теоретический материал, практических и исследовательских заданий, справочного материала. На уроках возможно использование компьютерных устных упражнений, применение тренажера устного счета.
Использование компьютерных технологий в преподавании математики позволяет непрерывно менять формы работы на уроке, постоянно чередовать устные и письменные упражнения, осуществлять разные подходы к решению математических задач, а это постоянно создает и поддерживает интеллектуальное напряжение учащихся, формирует у них устойчивый интерес к изучению данного предмета.
Место предмета «АЛГЕБРА» в учебном плане школы
Согласно школьному базисному учебному плану для изучения алгебры в 11 классе отводится не менее 102 часов из расчета 3 часов в неделю для отд. НИИФ. Независимо от профильной направленности школы и класса алгебра является обязательным предметом, в виду необходимости сдавать экзамен за 9, а затем и 11 классы.
Содержание программы по разделам курса алгебры 11 класса (Учебник Алгебра 10 – 11 классов, авт. Алимов Ш.А., Колягин Ю.М. и др., )
Занятия 3 часа в неделю.
Повторение. 4 часа
Числовые множества. Последовательности. Прогрессии.
Степенные функции четной и нечетной степени. Графики степенных функций с целой, дробной, положительной и отрицательной степенью.
. Взаимообратные функции и их свойства. Графики обратных функций.
Показательные функции. 6 часов, 1 С.р., 1 К.р.
Решение показательных уравнений и неравенств. Системы показательных уравнений и неравенств.
Логарифмические функции. 8 часов, 1 С.Р., 1 К.р.
Графики логарифмических функций. Формулы для преобразования логарифмических выражений. Решение логарифмических уравнений и неравенств. Решение систем логарифмических уравнений и неравенств.
Тригонометрические функции. 17 часов, 3 С.р., 1 К.р.
Области существования и значения тригонометрических функций.. Четность и нечетность тригонометрических функций. Периодичность тригонометрических функций. Графики тригонометрических функций. Формулы тригонометрических функций.
Тригонометрические уравнения. 9 часов, 3 С.р., 1 К.р.
Обратные тригонометрические функции. Преобразование тригонометрических выражений. Решение тригонометрических уравнений. Методы решения тригонометрических уравнений. Решение тригонометрических неравенств.
Предел функции 3 часа, 1 С.р.
Его иллюстрация на отдельных примерах. Определение.
Производная 6 часов, 1 С.р., 1 К.р.
Ее связь с пределом функции. Геометрический и физический смысл производной. Таблица правил дифференцирования для элементарных функций. Решение примеров на дифференцирование алгебраических функций.
Исследование алгебраических функций. 14 часов, 3 С.р., 1 К.р.
Области существования и значения функций. Четность и нечетность. Области возрастания и убывания функции. Периодичность функции. Нахождение экстремумов функции и точек перегибов. Особые точки функции. Построение эскизов графиков функций после их исследования.
Первообразная. 5 часов
Геометрический и физический смысл первообразной. Правила нахождения первообразной. Связь производной и первообразной. Совместная таблица формул производных и первообразных для элементарных функций.
Неопределенный и определенный интегралы. 23 часа, 4 С.р., 1 К.р.
Вычисление неопределенных интегралов. Формула Лейбница-Ньютона. Вычисление определенного интеграла. Нахождение площади геометрических фигур, ограниченных линиями осей и функциями. Нахождение объемов геометрических фигур.
Повторение некоторых тем. 8 часов, 1 К.р.
Подготовка к ЕГЭ. 7 часов
Тематическое планирование курса алгебры 11 класса
3 часа в неделю( 102 часа в год)
| № урока | ТЕМЫ | контроль | № недели |
|
| Тема 1 Повторение 4 часа |
|
|
| 1 | Числовые множества: натуральные, целые, рациональные, иррациональные, комплексные числа |
| 1 |
| 2 | Последовательности. Арифметическая и геометрическая прогрессии. Сумма n – членов прогрессии. |
| 1 |
| 3 | Взаимообратные функции и их свойства. Самостоятельная работа. | С.р. | 1 |
| 4 | Свойства и графики степенных функций с целыми, дробными, четными и нечетными показателями степени. |
| 2 |
|
| Тема 2 Показательные функции.6 часов |
|
|
| 5 | Свойства и графики показательных функций. |
| 2 |
| 6-7 | Решение показательных уравнений и неравенств. Самостоятельная работа. | С.р. | 2 и 3 |
| 8-9 | Решение систем из двух показательных уравнений или двух неравенств. |
| 3 |
| 10 | Контрольная работа №1 | К.р. | 4 |
|
| Тема 3 Логарифмические функции 8часов |
|
|
| 11 | Определение и свойства логарифмической функции. |
| 4 |
| 12 | Графики возрастающей и убывающей логарифмических функций. |
| 4 |
| 13 | Формулы для преобразования логарифмических выражений. Самостоятельная работа. | С.р. | 5 |
| 14-15 | Решение логарифмических уравнений и неравенств. |
| 5 |
| 16-17 | Решение систем логарифмических уравнений и неравенств. |
| 6 |
| 18 | Контрольная работа №2 | К.р. | 6 |
|
| Тема 4 Тригонометрические функции 17 часов |
|
|
| 19 | Тригонометрические тождества. |
| 7 |
| 20-21 | Взаимосвязь тригонометрических функций через тождества. Самостоятельная работа. | С.р. | 7 |
| 22 | Четность и нечетность. Периодичность тригонометрических функций. |
| 8 |
| 23 | Графики тригонометрических функций. |
| 8 |
| 24 | Формулы приведения и их назначение. Решение примеров. Самостоятельная работа. | С.р. | 8 |
| 25-26 | Формулы тригонометрических функций суммы и разности двух углов. Решение примеров |
| 9 |
| 27-28 | Формулы двойного угла. Формулы понижения степени функции. Самостоятельная работа. | С.р. | 9 и 10 |
| 29-30 | Формулы суммы и разности двух функций с разными углами. Решение примеров |
| 10 |
| 31-32 | Формулы произведений двух тригонометрических функций с разными углами. Самостоятельная работа. | С.р. | 11 |
| 33-34 | Решение примеров на преобразования тригонометрических выражений и доказательства тождеств. |
| 11 и 12 |
| 35 | Контрольная работа №3 | К.р. | 12 |
|
| Тема 5 Тригонометрические уравнения 9 часов |
|
|
| 36-37 | Обратные тригонометрические функции и их свойства. Решение примеров. |
| 12 и 13 |
| 38-39 | Преобразования тригонометрических уравнений и разложение их на множители. Решение примеров. Самостоятельная работа. | С.р. | 13 |
| 40-41 | Методы решения тригонометрических уравнений. Решение примеров Самостоятельная работа | С.р. | 14 |
| 42-43 | Тригонометрические неравенства и их решение. Решение примеров. |
| 14 и 15 |
| 44 | Контрольная работа №4 | К.р. | 15 |
|
| Тема 6 Пределы 3 часа |
|
|
| 45 | Определение предела последовательности и функции. |
| 15 |
| 46-47 | Назначение пределов. Примеры, связанные с определением пределов. Самостоятельная работа. | С.р. | 16 |
|
| Тема 7 Производная 6 часов |
|
|
| 48 | Геометрический и физический смысл производной |
| 16 |
| 49-50 | Таблица правил дифференцирования (взятие производной) элементарных функций. Самостоятельная работа. | С.р. | 17 |
| 51-52 | Решение примеров на дифференцирование функций. |
| 17 и 18 |
| 53 | Контрольная работа №5 | К.р. | 18 |
|
| Тема 8 Исследование алгебраических функций 14 часов |
|
|
| 54-55 | Области существования и значений функции. Решение примеров. Самостоятельная работа. | С.р. | 18 и 19 |
| 56 | Четность и нечетность функций. |
| 19 |
| 57 | Периодичность функций. Самостоятельная работа. | С.р. | 19 |
| 58-59 | Применение производной при исследовании функции. Нахождение экстремумов функций, точек перегибов. |
| 20 |
| 60-61 | Нахождение интервалов монотонности: возрастания и убывания функции. Решение примеров. Самостоятельная работа. | С.р. | 20 и 21 |
| 62-63 | Особые точки и значение функции в этих точках. Решение примеров. |
| 21 |
| 64-66 | Построение эскизов графиков функций после их исследования. Решение примеров. Самостоятельная работа. |
| 22 |
| 67 | Контрольная работа №6 | К.р. | 23 |
|
| Тема 5 Первообразная 5 часов |
|
|
| 68 | Геометрический и физический смысл первообразной |
| 23 |
| 69 | Правила нахождения первообразной |
| 23 |
| 70 | Связь производной и первообразной |
| 24 |
| 71-72 | Таблица формул производных и первообразных для элементарных функций.. |
| 24 |
|
| Тема 10 Неопределенный и определенный интеграл 23 часа |
|
|
| 73-76 | Вычисление неопределенного интеграла. Примеры Самостоятельная работа | С.р. | 25 и 26 |
| 77 | Формула Лейбница-Ньютона. |
| 26 |
| 78-80 | Вычисление определенного интеграла. Примеры . Самостоятельная работа. | С.р. | 26 и 27 |
| 81 | Контрольная работа. № 7 | К.р. | 27 |
| 82-84 | Нахождение площади геометрической фигуры Примеры. Самостоятельная работа. | С.р. | 28 |
| 85-87 | Нахождение объема геометрической фигуры. Примеры. Самостоятельная работа. | С.р. | 29 |
|
| Тема 11 Повторение некоторых тем 8 часов |
|
|
| 88-89 | Показательные функции и уравнения |
| 30 |
| 90-91 | Логарифмические функции и уравнения |
| 30 и 31 |
| 92-94 | Тригонометрические функции и уравнения |
| 31 и 32 |
| 95 | Итоговая контрольная работа | К.р. | 32 |
|
| Подготовка к ЕГЭ 7 часов |
|
|
| 96-102 | Решение вариантов заданий ЕГЭ |
| 32,33,34 |
|
|
|
|
|
Самостоятельных работ – 18
Контрольных работ - 8
Формы и средства контроля.
Основными методами проверки знаний и умений учащихся по алгебре являются устный опрос, письменные работы. К письменным формам контроля относятся: математические диктанты, самостоятельные и контрольные работы, тесты. Основные виды проверки знаний – текущая и итоговая. Текущая проверка проводится систематически из урока в урок, а итоговая – по завершении темы (раздела), школьного курса.
Типы индивидуальных консультаций и прием зачетов в отд. НИИФ
Выявление и ликвидация пробелов в знаниях обучающихся
Подготовка к изучению нового материала
Решение задач практического содержания и задач повышенной трудности
Подготовка к контрольной работе
Формы и методы проведения зачета:
Устно-индивидуальный опрос по карточкам-заданиям
Тест
Групповое собеседование
Письменный зачет
Устно-письменный зачет
Письменные ответы на вопросы
Перечень учебно-методических средств обучения
Для учащихся:
Алимов Ш.А. и др. Алгебра. Учебник для 10-11 классов общеобразовательных учреждений. М., «Просвещение», 2007.).
Для учителя:
Коваленко В.Г., Дидактические игры на уроках математики. Книга для учителя. М.: «Просвещение», 1990
Макарова Л.В. Математические диктанты в VII-VIII классах «Математика в школе»,1999. №3,с.27
Буланова Л. М., Дудницын Ю. П. Проверочные задания по математике для учащихся 5-8 и 10 классов. – М.: Просвещение, 1998.
Жохов В. И., Макарычкв Ю. Н., Миндюк Н. Г. Дидактические материалы по алгебре,8 класс. – М.: Просвещение, 2000
Денищева Л.О и др. Зачёты в системе дифференцированного обучения математике.- М.: Просвещение, 1993.
Выгодский М.Я. Справочник по элементарной математике — М.: ООО «Издательство Астрель»: ООО «Издательство АСТ», 2003.
Никольский С.Н. Математика: Школьная энциклопедия — М.: Большая Российская энциклопедия; Дрофа, 1997.
Для поддержки учебного процесса предполагается использовать интернет-ресурсы и электронные носители информации (СД- и ДВД-диски)
1С: Школа. Математика 5-11класс. Практикум
Министерство образования РФ: http://www.ed.gov.ru/ ; http://www.edu.ru
Тестирование online: 5 - 11 классы: http://www.kokch.kts.ru/cdo
Педагогическая Сеть «Методисты.ру» Математика в школе
Новые технологии в образовании: http://edu.secna.ru/main
Путеводитель «В мире науки» для школьников: http://www.uic.ssu.samara.ru
Мегаэнциклопедия Кирилла и Мефодия: http://mega.km.ru
сайты «Энциклопедий»: http://www.rubricon.ru/; http://www.encyclopedia.ru
сайт для самообразования и он-лайн тестирования: http://uztest.ru/
досье школьного учителя математики: http://www.mathvaz.ru/
Сайт учителя математики Шапошникова И.М.


 Получите свидетельство
Получите свидетельство Вход
Вход


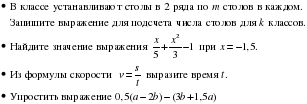
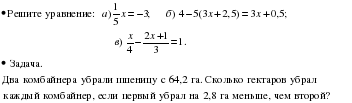

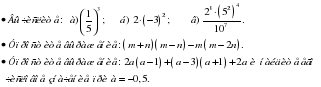
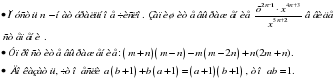
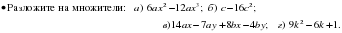
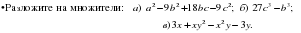
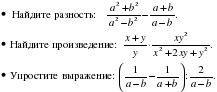
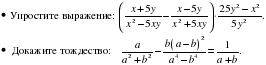
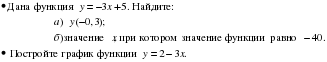
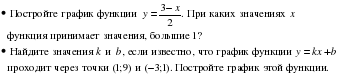
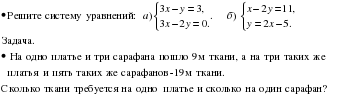


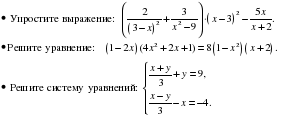










 Рабочие программы по алгебре (7-11 классы) (0.18 MB)
Рабочие программы по алгебре (7-11 классы) (0.18 MB)
 0
0 593
593 21
21 Нравится
0
Нравится
0







