Рабочая программа учебного курса по алгебре
8 «» класс
Учебник «Алгебра», 8 класс,
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Пояснительная записка
Статус документа
Рабочая программа по алгебре в 8 классе составлена на основе федерального компонента государственного стандарта и примерной программы основного общего образования.
Рабочая программа конкретизирует содержание предметных тем образовательного стандарта и распределение учебных часов по разделам курса.
Структура документа
Рабочая программа включает три раздела: пояснительную записку, цели, основное содержание с примерным распределением учебных часов по разделам курса; кол-во контрольных работ, требования к уровню подготовки выпускников, УМК
Общая характеристика предмета
Алгебра нацелена на формирование математического аппарата для решения задач по математике, смежных предметов, окружающей реальности. Язык алгебры подчеркивает значение математики как языка для построения математических моделей, процессов и явлений реального мира. Одной из основных задач изучения алгебры является развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики; овладение навыками дедуктивных рассуждений. Преобразование символических форм вносит свой специфический вклад в развитие воображения, способностей к математическому творчеству. Другой важной задачей изучения алгебры является получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов (равномерных, равноускоренных, экспоненциальных, периодических и др.), для формирования у учащихся представлений о роли математики в развитии цивилизации и культуры.
Цели предмета:
-овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучение смежных дисциплин, продолжении образования;
-развитие таких качеств личности, как ясность и точность мысли, логическое мышление, пространственное воображение, алгоритмическая культура, интуиция, критичность и самокритичность;
-формирование представлений об идеях и методах математики как универсального языка науки и техники, средстве моделирования процессов и явлений;
-воспитания средствами математики культуры личности, знакомство с жизнью и деятельностью видных отечественных и зарубежных ученых-математиков, понимание значимости математики для общественного прогресса.
Задачи предмета:
-развить представление о числе и роли вычислений в человеческой практике; сформировать практические навыки выполнения устных, письменных инструментальных вычислений, развить вычислительную культуру;
-овладеть символическим языком алгебры, выработать формально-оперативные алгебраические умения и научиться применять их к решению математических и нематематических задач;
-изучить свойства и графики элементарных функций, научиться использовать функционально-графические представления для описания и анализа реальных зависимостей;
-развить логическое мышление и речь – умения логически обосновывать суждения, проводить несложные систематизации. Приводить примеры и контрпримеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства.
-сформировать представления об изучаемых понятиях и методах как важнейших средствах математического моделирования реальных процессов и явлений.
Предполагаемые формы обучения
К формам и методам обучения можно отнести классно-урочную систему, практические занятия, решение качественных задач, исследовательская деятельность, применение мультимедийных презентаций, коллективная и индивидуальная работа, работа в группах и парах.
Результаты обучения
Результаты обучения представлены в требованиях к уровню подготовки и задают систему итоговых результатов обучения, которых должны достигать все учащиеся, оканчивающие основную школу, и достижение которых является обязательным условием положительной аттестации ученика за курс основной школы. Эти требования структурированы по трем компонентам: «знать/понимать», «уметь», «использование приобретенных знаний и умений в повседневной жизни и практической деятельности».
Место предмета в федеральном базисном учебном плане
Согласно федеральному базисному учебному плану для образовательных учреждений Российской Федерации на изучение алгебры отводится 102 часа из расчета 3 часа в неделю.
Учебно-тематический план
| № п./п. | Разделы программы | Количество часов |
| 1. | Глава 1. Рациональные дроби | 23 |
| 2. | Глава 2. Квадратные корни | 17 |
| 3. | Глава 3. Квадратные уравнения | 22 |
| 4. | Глава 4. Неравенства | 18 |
| 5. | Глава 5. Степень с целым показателем. Элементы статистики | 16 |
| 6. | Повторение | 6 |
Содержание обучения
1. Рациональные дроби (23 урока)
Рациональная дробь. Основное свойство дроби, сокращение дробей.
Тождественные преобразования рациональных выражений. Функция у = k/x и ее график.
Основная цель – выработать умение выполнять тождественные преобразования рациональных выражений.
Так как действия с рациональными дробями существенным образом опираются на действия с многочленами, то в начале темы необходимо повторить с учащимися преобразования целых выражений.
Главное место в данной теме занимают алгоритмы действий с дробями. Учащиеся должны понимать, что сумму, разность, произведение и частное дробей всегда можно представить в виде дроби. Приобретаемые в данной теме умения выполнять сложение, вычитание, умножение и деление дробей являются опорными в преобразованиях дробных выражений. Поэтому им следует уделить особое внимание. Нецелесообразно переходить к комбинированным заданиям на все действия с дробями прежде, чем будут усвоены основные алгоритмы. Задания на все действия с дробями не должны быть излишне громоздкими и трудоемкими.
При нахождении значений дробей даются задания на вычисления с помощью калькулятора. В данной теме расширяются сведения о статистических характеристиках. Вводится понятие среднего гармонического ряда положительных чисел. Изучение темы завершается рассмотрением свойств графика функции у = k/x.
2. Квадратные корни (17 уроков)
Понятие об иррациональных числах. Общие сведения о действительных числах. Квадратный корень. Понятие о нахождении приближенного значения квадратного корня. Свойства квадратных корней. Преобразования выражений, содержащих квадратные корни. Функция 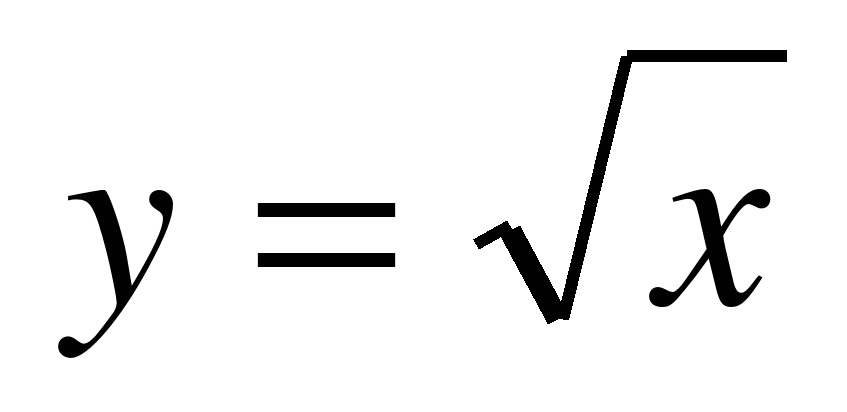 , ее свойства и график.
, ее свойства и график.
Основная цель – систематизировать сведения о рациональных числах и дать представление об иррациональных числах, расширив тем самым понятие о числе; выработать умение выполнять преобразования выражений, содержащих квадратные корни.
В данной теме учащиеся получают начальное представление о понятии действительного числа. С этой целью обобщаются известные учащимся сведения о рациональных числах. Для введения понятия иррационального числа используется интуитивное представление о том, что каждый отрезок имеет длину и потому каждой точке координатной прямой соответствует некоторое число. Показывается, что существуют точки, не имеющие рациональных абсцисс.
При введении понятия корня полезно ознакомить учащихся с нахождением корней с помощью калькулятора.
Основное внимание уделяется понятию арифметического квадратного корня и свойствам арифметических квадратных корней. Доказываются теоремы о корне из произведения и дроби, а также тождество 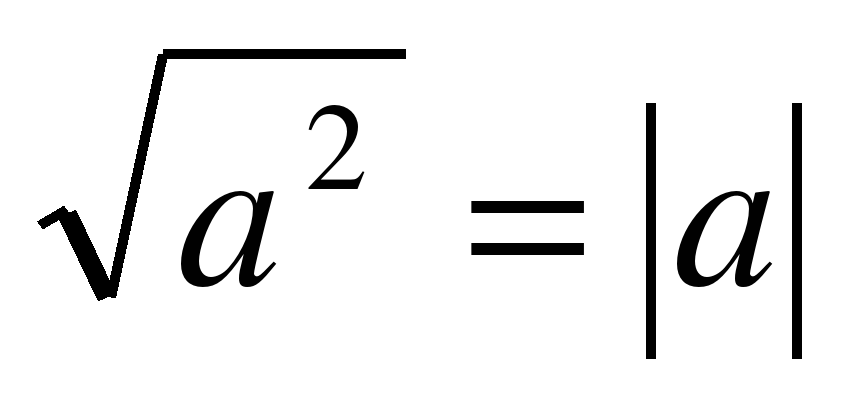 , которые получают применение в преобразованиях выражений, содержащих квадратные корни. Специальное внимание уделяется освобождению от иррациональности в знаменателе дроби в выражениях вида
, которые получают применение в преобразованиях выражений, содержащих квадратные корни. Специальное внимание уделяется освобождению от иррациональности в знаменателе дроби в выражениях вида 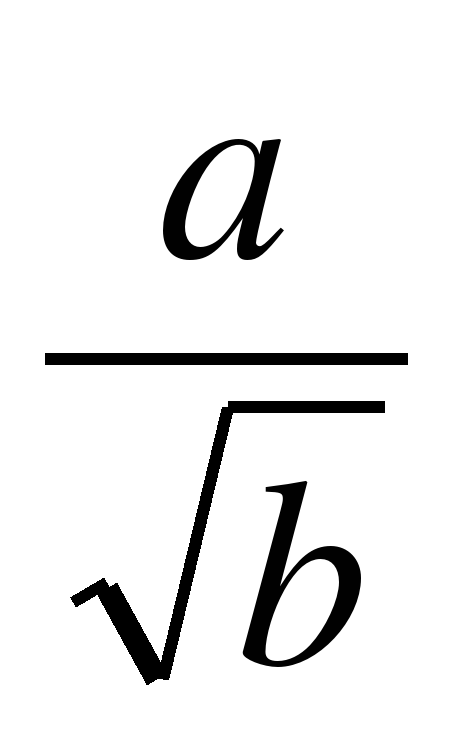 ,
, 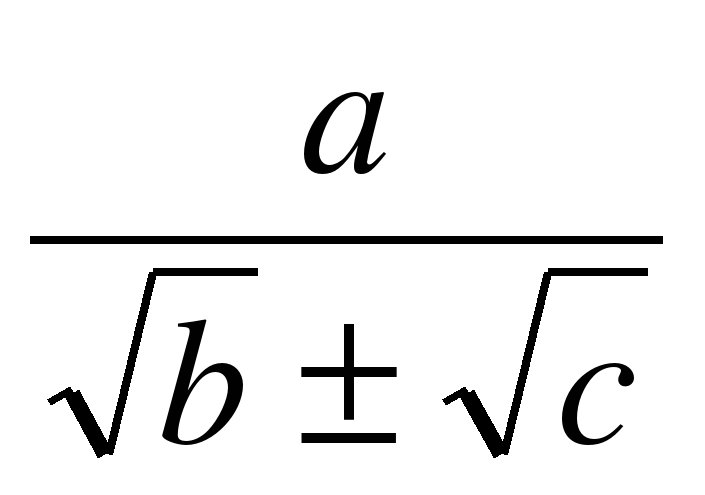 Умение преобразовывать выражения, содержащие корни, часто используется как в самом курсе алгебры, так и в курсах геометрии, алгебры и начал анализа.
Умение преобразовывать выражения, содержащие корни, часто используется как в самом курсе алгебры, так и в курсах геометрии, алгебры и начал анализа.
Продолжается работа по развитию функциональных представлений учащихся. Рассматриваются функция 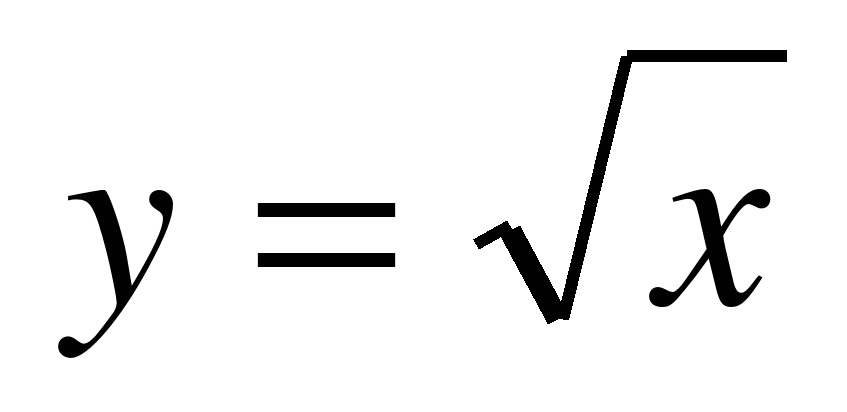 , ее свойства и график. При изучении функции
, ее свойства и график. При изучении функции 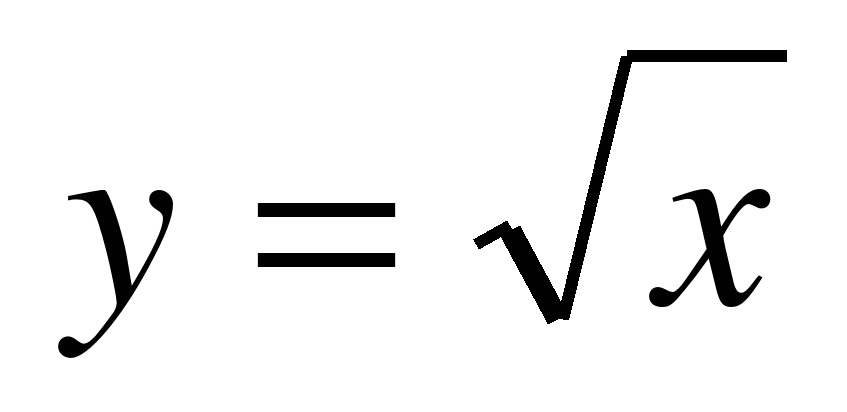 показывается ее взаимосвязь с функцией
показывается ее взаимосвязь с функцией 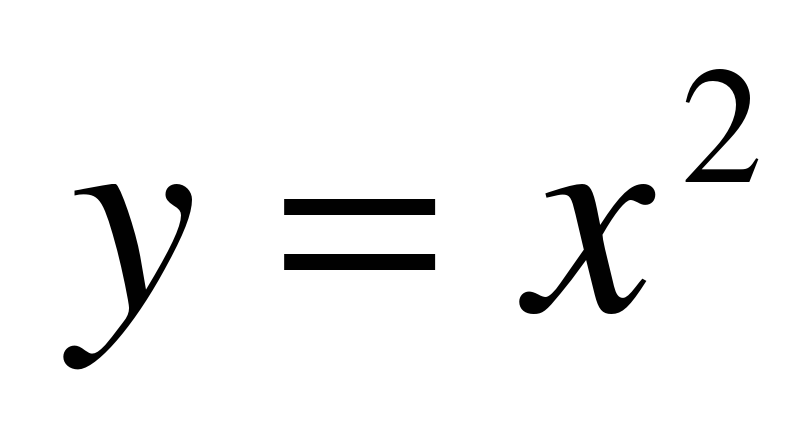 , где
, где 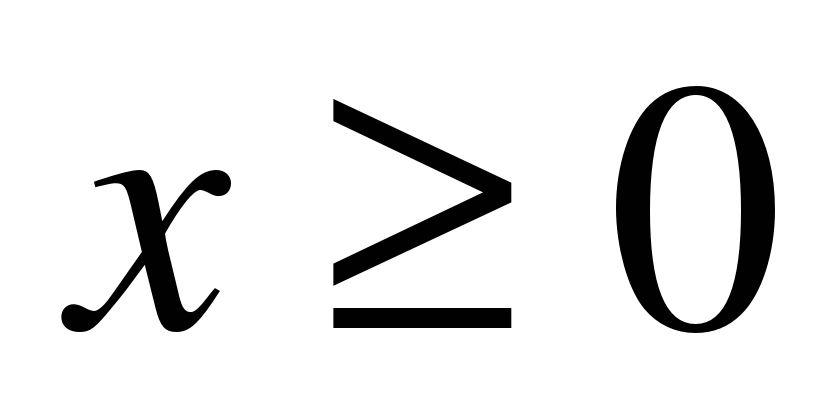
3. Квадратные уравнения (22 урока)
Квадратное уравнение. Формула корней квадратного уравнения. Решение рациональных уравнений. Решение задач, приводящих к квадратным уравнениям и простейшим рациональным уравнениям.
Основная цель — выработать умения решать квадратные уравнения и простейшие рациональные уравнения и применять их к решению задач.
В начале темы приводятся примеры решения неполных квадратных уравнений. Этот материал систематизируется. Рассматриваются алгоритмы решения неполных квадратных уравнений различного вида.
Основное внимание следует уделить решению уравнений вида ах2 + bx + с = 0, где а 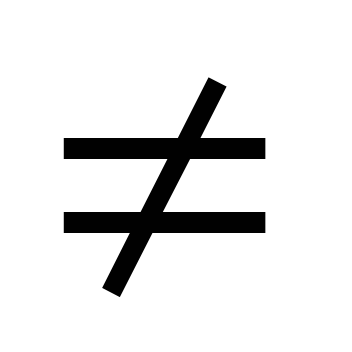 0, с использованием формулы корней. В данной теме учащиеся знакомятся с формулами Виета, выражающими связь между корнями квадратного уравнения и его коэффициентами. Они используются в дальнейшем при доказательстве теоремы о разложении квадратного трехчлена на линейные множители.
0, с использованием формулы корней. В данной теме учащиеся знакомятся с формулами Виета, выражающими связь между корнями квадратного уравнения и его коэффициентами. Они используются в дальнейшем при доказательстве теоремы о разложении квадратного трехчлена на линейные множители.
Учащиеся овладевают способом решения дробных рациональных уравнений, который состоит в том, что решение таких уравнений сводится к решению соответствующих целых уравнений с последующим исключением посторонних корней.
Изучение данной темы позволяет существенно расширить аппарат уравнений, используемых для решения текстовых задач.
4. Неравенства (18 уроков)
Числовые неравенства и их свойства. Почленное сложение и умножение числовых неравенств. Погрешность и точность приближения. Линейные неравенства с одной переменной и их системы.
Основная цель — ознакомить учащихся с применением неравенств для оценки значений выражений, выработать умение решать линейные неравенства с одной переменной и их системы.
Свойства числовых неравенств составляют ту базу, на которой основано решение линейных неравенств с одной переменной. Теоремы о почленном сложении и умножении неравенств находят применение при выполнении простейших упражнений на оценку выражений по методу границ. Вводятся понятия абсолютной погрешности и точности приближения, относительной погрешности.
Умения проводить дедуктивные рассуждения получают развитие как при доказательствах указанных теорем, так и при выполнении упражнений на доказательства неравенств.
В связи с решением линейных неравенств с одной переменной дается понятие о числовых промежутках, вводятся соответствующие названия и обозначения. Рассмотрению систем неравенств с одной переменной предшествует ознакомление учащихся с понятиями пересечения и объединения множеств.
При решении неравенств используются свойства равносильных неравенств, которые разъясняются на конкретных примерах. Особое внимание следует уделить отработке умения решать простейшие неравенства вида ах b, ах b, остановившись специально на случае, когда а 0.
В этой теме рассматривается также решение систем двух линейных неравенств с одной переменной, в частности таких, которые записаны в виде двойных неравенств.
5. Степень с целым показателем. Элементы статистики (16 уроков)
Степень с целым показателем и ее свойства. Стандартный вид числа. Начальные сведения об организации статистических исследований.
Основная цель — выработать умение применять свойства степени с целым показателем в вычислениях и преобразованиях, сформировать начальные представления о сборе и группировке статистических данных, их наглядной интерпретации.
В этой теме формулируются свойства степени с целым показателем. Метод доказательства этих свойств показывается на примере умножения степеней с одинаковыми основаниями. Дается понятие о записи числа в стандартном виде. Приводятся примеры использования такой записи в физике, технике и других областях знаний.
Учащиеся получают начальные представления об организации статистических исследований. Они знакомятся с понятиями генеральной и выборочной совокупности. Приводятся примеры представления статистических данных в виде таблиц частот и относительных частот. Учащимся предлагаются задания на нахождение по таблице частот таких статистических характеристик, как среднее арифметическое, мода, размах. Рассматривается вопрос о наглядной интерпретации статистической информации. Известные учащимся способы наглядного представления статистических данных с помощью столбчатых и круговых диаграмм расширяются за счет введения таких понятий, как полигон и гистограмма.
Повторение (9 уроков)
Контрольных работ - 10
1. Рациональные дроби. Сложение и вычитание дробей.
2. Рациональные дроби. Все действия с дробями.
3. Арифметический квадратный корень и его свойства.
4. Применение свойств арифметического квадратного корня.
5. Квадратные уравнения.
6. Дробно рациональные уравнения.
7. Числовые неравенства и их свойства.
8. Линейные неравенства и системы неравенств с одной переменной.
9. Степень с целым показателем.
10.Итоговая контрольная работа.
Требования к уровню подготовки.
В результате изучения алгебры в 8 классе ученик должен знать, уметь, понимать.
Рациональные дроби.
Знать:
Уметь:
распознавать рациональную дробь среди других буквенных выражений;
приводить примеры рациональных дробей;
находить множество допустимых значений переменных, входящих в данную дробь;
сокращать дроби;
выполнять действия с рациональными дробями.
строить график функции у = k/x.
Квадратные корни.
Знать/понимать:
Уметь:
извлекать квадратные корни;
оценивать не извлекающиеся корни;
находить приближенные значения корней;
записывать свойства в символической форме;
применять свойства арифметических квадратных корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни.
Квадратные уравнения.
Знать
определение квадратного уравнения;
формулу корней квадратного уравнения;
термин «неполное квадратное уравнение»;
приемы решения квадратного уравнения;
формулы Виета.
Уметь:
записывать квадратное уравнение в общем виде;
свободно владеть терминологией;
решать квадратные уравнения по формуле;
распознавать и решать неполные квадратные уравнения;
применять теорему Виета для решения упражнений.
Неравенства.
Знать: понятия равносильности неравенств.
Уметь:
применять свойства неравенств для перехода от одних неравенств к другим;
решать линейные неравенства;
изображать множества решений линейного неравенства;
решать системы линейных неравенств.
Степень с целым показателем.
Знать:
Уметь: вычислять значения выражений, содержащих степени.
Литература:
1. Жохов В.И., Макарычев Ю.Н., Миндюк Н.Г. Дидактический материал по алгебре для 8 класса. М.,2004
2. Жохов В.И, Карташева Г.Д. Уроки алгебры в 8 классе. Пособие для учителя, М. 2004
3. Жохов В.И, Карташева Г.Д Алгебра, 8.Карточки для проведения контрольных работ.
М.,2003
4. Мерзляк А.Г., Полонский В.Б., Рабинович Е.М., Якир М.С.Сборник задач и контрольных работ для 8 класса. М. 2004
5. Ершова А.И., Голобородько В.В, Ершова А.С. Алгебра и геометрия 8,самостоятельные и контрольные работы. М. 2007
6. Алгебра-8 Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова под редакцией С.А. Теляковского.
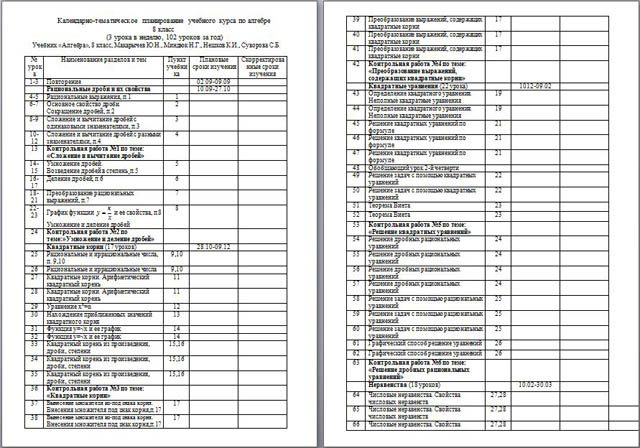
Календарно-тематическое планирование учебного курса по алгебре
8 класс
(3 урока в неделю, 102 уроков за год)
Учебник «Алгебра», 8 класс, Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
| № урока | Наименование разделов и тем | Пункт учебника | Плановые сроки изучения | Скорректированные сроки изучения |
|
| 1-3 | Повторение |
| 02.09-09.09 |
|
|
|
| Рациональные дроби и их свойства |
| 10.09-27.10 |
|
|
| 4-5 | Рациональные выражения, п.1 | 1 |
|
|
|
| 6-7 | Основное свойство дроби. Сокращение дробей, п.2 | 2 |
|
|
|
| 8-9 | Сложение и вычитание дробей с одинаковыми знаменателями, п.3 | 3 |
|
|
|
| 10-12 | Сложение и вычитание дробей с разными знаменателями, п.4 | 4 |
|
|
|
| 13 | Контрольная работа №1 по теме: «Сложение и вычитание дробей» |
|
|
|
|
| 14-15 | Умножение дробей. Возведение дробей в степень¸п.5 | 5 |
|
|
|
| 16-17 | Деление дробей, п.6 | 6 |
|
|
|
| 18-21 | Преобразование рациональных выражений, п.7 | 7 |
|
|
|
| 22-23 | График функции 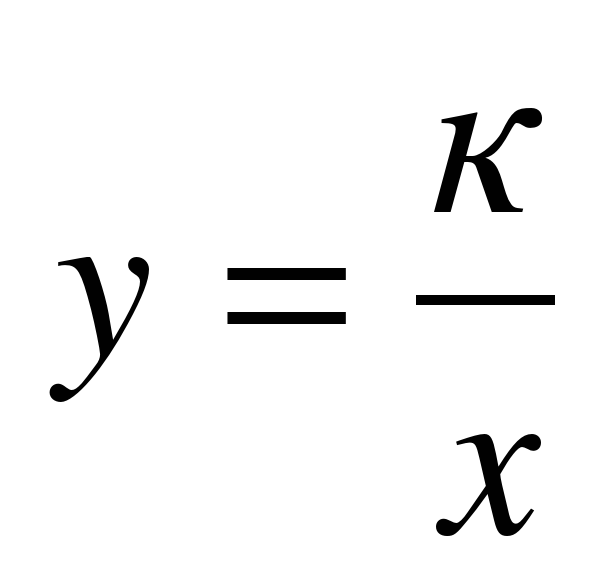 и ее свойства, п.8 и ее свойства, п.8 Умножение и деление дробей | 8 |
|
|
|
| 24 | Контрольная работа №2 по теме:»Умножение и деление дробей» |
|
|
|
|
|
| Квадратные корни (17 уроков) |
| 28.10-09.12 |
|
|
| 25 | Рациональные и иррациональные числа, п. 9,10 | 9,10 |
|
|
|
| 26 | Рациональные и иррациональные числа | 9,10 |
|
|
|
| 27 | Квадратные корни. Арифметический квадратный корень | 11 |
|
|
|
| 28 | Квадратные корни. Арифметический квадратный корень | 11 |
|
|
|
| 29 | Уравнение x²=α | 12 |
|
|
|
| 30 | Нахождение приближенных значений квадратного корня | 13 |
|
|
|
| 31 | Функция y=√x и ее график | 14 |
|
|
|
| 32 | Функция y=√x и ее график | 14 |
|
|
|
| 33 | Квадратный корень из произведения‚ дроби‚ степени | 15,16 |
|
|
|
| 34 | Квадратный корень из произведения‚ дроби‚ степени | 15,16 |
|
|
|
| 35 | Квадратный корень из произведения‚ дроби‚ степени | 15,16 |
|
|
|
| 36 | Контрольная работа №3 по теме: «Квадратные корни» |
|
|
|
|
| 37 | Вынесение множителя из-под знака корня. Внесения множителя под знак корня,п.17 | 17 |
|
|
|
| 38 | Вынесение множителя из-под знака корня. Внесения множителя под знак корня,п.17 | 17 |
|
|
|
| 39 | Преобразование выражений, содержащих квадратные корни | 17 |
|
|
|
| 40 | Преобразование выражений, содержащих квадратные корни | 17 |
|
|
|
| 41 | Преобразование выражений, содержащих квадратные корни | 17 |
|
|
|
| 42 | Контрольная работа №4 по теме: «Преобразование выражений, содержащих квадратные корни» |
|
|
|
|
|
| Квадратные уравнения (22 урока) |
| 1012-09.02 |
|
|
| 43 | Определение квадратного уравнения. Неполные квадратные уравнения | 19 |
|
|
|
| 44 | Определение квадратного уравнения. Неполные квадратные уравнения | 19 |
|
|
|
| 45 | Решение квадратных уравнений по формуле | 21 |
|
|
|
| 46 | Решение квадратных уравнений по формуле | 21 |
|
|
|
| 47 | Решение квадратных уравнений по формуле | 21 |
|
|
|
| 48 | Обобщающий урок 2-й четверти |
|
|
|
|
| 49 | Решение задач с помощью квадратных уравнений | 22 |
|
|
|
| 50 | Решение задач с помощью квадратных уравнений | 22 |
|
|
|
| 51 | Теорема Виета | 23 |
|
|
|
| 52 | Теорема Виета | 23 |
|
|
|
| 53 | Контрольная работа №5 по теме: «Решение квадратных уравнений» |
|
|
|
|
| 54 | Решение дробных рациональных уравнений | 24 |
|
|
|
| 55 | Решение дробных рациональных уравнений | 24 |
|
|
|
| 56 | Решение дробных рациональных уравнений | 24 |
|
|
|
| 57 | Решение дробных рациональных уравнений | 24 |
|
|
|
| 58 | Решение задач с помощью рациональных уравнений | 25 |
|
|
|
| 59 | Решение задач с помощью рациональных уравнений | 25 |
|
|
|
| 60 | Решение задач с помощью рациональных уравнений | 25 |
|
|
|
| 61 | Графический способ решение уравнений | 26 |
|
|
|
| 62 | Графический способ решение уравнений | 26 |
|
|
|
| 63 | Контрольная работа №6 по теме: «Решение дробных рациональных уравнений» |
|
|
|
|
|
| Неравенства (18 уроков) |
| 10.02-30.03 |
|
|
| 64 | Числовые неравенства. Свойства числовых неравенств | 27,28 |
|
|
|
| 65 | Числовые неравенства. Свойства числовых неравенств | 27,28 |
|
|
|
| 66 | Числовые неравенства. Свойства числовых неравенств | 27,28 |
|
|
|
| 67 | Числовые неравенства. Свойства числовых неравенств | 27,28 |
|
|
|
| 68 | Сложение и умножение числовых неравенств | 29 |
|
|
|
| 69 | Сложение и умножение числовых неравенств | 29 |
|
|
|
| 70 | Сложение и умножение числовых неравенств | 29 |
|
|
|
| 71 | Контрольная работа №7 по теме: «Числовые неравенства» |
|
|
|
|
| 72 | Числовые промежутки | 30 |
|
|
|
| 73 | Числовые промежутки | 30 |
|
|
|
| 74 | Решение неравенств с одной переменной | 31 |
|
|
|
| 75 | Решение неравенств с одной переменной | 31 |
|
|
|
| 76 | Решение неравенств с одной переменной | 31 |
|
|
|
| 77 | Решение неравенств с одной переменной | 31 |
|
|
|
| 78 | Обобщающий урок 3-й четверти |
|
|
|
|
| 79 | Решение систем неравенств с одной переменной | 32 |
|
|
|
| 80 | Решение систем неравенств с одной переменной | 32 |
|
|
|
| 81 | Решение систем неравенств с одной переменной | 32 |
|
|
|
| 82 | Контрольная работа №8 по теме: «Решение неравенств с одной переменной» |
|
|
|
|
|
| Степень с целым показателям (16 уроков) |
| 01.04-15.05 |
|
|
| 83 | Определение степени с целым отрицательным показателем | 33 |
|
|
|
| 84 | Определение степени с целым отрицательным показателем | 33 |
|
|
|
| 85 | Свойства степени с целым показателем | 34 |
|
|
|
| 86 | Свойства степени с целым показателем | 34 |
|
|
|
| 87 | Стандартный вид числа | 35 |
|
|
|
| 88 | Стандартный вид числа | 35 |
|
|
|
| 89 | Запись приближенных значений | 36 |
|
|
|
| 90 | Запись приближенных значений | 36 |
|
|
|
| 91 | Действия над приближенными значениями | 37 |
|
|
|
| 92 | Действия над приближенными значениями | 37 |
|
|
|
| 93 | Вычисления с приближенными данными на микрокалькуляторе | 38 |
|
|
|
| 94 | Вычисления с приближенными данными на микрокалькуляторе | 38 |
|
|
|
| 95 | Контрольная работа №9 по теме: «Степень с целым показателем» |
|
|
|
|
| 96 | Итоговое повторение курса алгебры 8 класса.
|
| 17.05-28.05 |
|
|
| 97 | Итоговое повторение курса алгебры 8 класса |
|
|
|
|
| 98 | Итоговое повторение курса алгебры 8 класса |
|
|
|
|
| 99 | Итоговое повторение курса алгебры 8 класса |
|
|
|
|
| 100 | Итоговое повторение курса алгебры 8 класса |
|
|
|
|
| 101 | Контрольная работа №10 |
|
|
|
|
| 102 | Анализ контрольной работы. |
|
|
|
|
|
| Итого: 102 часа |
|
|
|
|

 Получите свидетельство
Получите свидетельство Вход
Вход











 Рабочая программа учебного курса по алгебре (8 класс) (0.18 MB)
Рабочая программа учебного курса по алгебре (8 класс) (0.18 MB)
 0
0 596
596 52
52 Нравится
0
Нравится
0






