| ДЕПАРТАМЕНТ ОБРАЗОВАНИЯ АДМИНИСТРАЦИИ ПУРОВСКОГО РАЙОНА
МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ "СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА № 2" П.Г.Т. УРЕНГОЙ ПУРОВСКОГО РАЙОНА |
| микрорайон 5, д.№ 53а, п.г.т.Уренгой, Пуровский район, Ямало-Ненецкий автономный округ, Россия, 629860, тел. (34934) 9-27-45, факс 9-25-67. Е-mail: Urengoу[email protected] ОКПО 32733321, ОГРН 1028900859558, ИНН/КПП 8911012478/ 891101001, БИК 047191000
|
|
| УТВЕРЖДАЮ Директор МБОУ «СОШ № 2» п.г.т. Уренгой _____ Е.В. Крепешева Приказ № 207 от «30» августа 2014 г.
|
РАБОЧАЯ ПРОГРАММА ПЕДАГОГА
Чолкован Алены Викторовны, высшая квалификационная категория
(Ф.И.О., категория)
по математике для 8 класса, срок реализации – 1 год
(предмет, класс и т.п.)
СОГЛАСОВАНО Рассмотрено на заседании
Зам. директора по методического объединения
образовательному процессу протокол № 1 от
__________ Кузяева Н.В. «30» августа 2014 г.
____ Исько И.А., руководитель МО
п.г.т. Уренгой
2014 - 2015 учебный год
Пояснительная записка
Настоящая программа составлена в соответствии с федеральным компонентом стандарта основного общего образования по математике, обязательными минимумами содержания основных образовательных программ, требованиями к уровню подготовки выпускников на основе примерной программы основного общего образования по математике (М.: Просвещение, 2011 г.) и программы курса алгебры авторов Зубаревой И.И. и Мордковича А.Г. (М.: Мнемозина, 2009 г.) и программы курса геометрии 7-9 классы составитель Т.А. Бурмистрова (М.: Просвещение, 2008 г.).
Изучение курса алгебры нацелено на формирование математического аппарата для решения задач из математики, смежных предметов, окружающей реальности. Язык алгебры подчеркивает значение математики как языка для построения математических моделей, процессов и явлений реального мира одной из основных задач изучения алгебры является развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики; овладение навыками дедуктивных рассуждений. Преобразование символических форм вносит свой специфический вклад в развитие воображения, способностей к математическому творчеству. Другой важной задачей изучения алгебры является получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов (равномерных, равноускоренных, экспоненциальных, периодических и др.), для формирования у обучающихся представлений о роли математики в развитии цивилизации и культуры.
Геометрия — один из важнейших компонентов математического образования, необходимый для приобретения конкретных знаний о пространстве и практически значимых умений, формирования языка описания объектов окружающего мира, для развития пространственного воображения и интуиции, математической культуры, для эстетического воспитания учащихся. Изучение геометрии вносит вклад в развитие логического мышления, в формирование понятия доказательства.
Таким образом, в ходе освоения содержания курса учащиеся получают возможность развить пространственные представления и изобразительные умения, освоить основные факты и методы планиметрии, познакомиться с простейшими фигурами и их свойствами.
В программу внесены изменения в связи с тем, что алгебра и геометрия преподаются одним предметом математика. В связи с этим предусмотрено последовательное изучение тематических блоков с чередованием материала по алгебре и геометрии. Каждый блок заканчивается контрольной работой.
Цель изучения курса алгебры в 8 классе - овладение математическими знаниями и умениями, необходимыми для продолжения обучения в старшей школе или иных общеобразовательных учреждениях, изучения смежных дисциплин, применения в повседневной жизни.
Задачи курса алгебры:
Формирование представлений о многочлене от одной переменной, алгебраической дроби, о рациональном выражении; о функции у = ах2 , функции у = 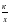 , гиперболе, перемещении графика по координатной плоскости, квадратичной функции
, гиперболе, перемещении графика по координатной плоскости, квадратичной функции 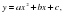 ; о квадратном корне из неотрицательного числа, о функции
; о квадратном корне из неотрицательного числа, о функции 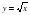 ; о полном, приведенном, неполном квадратном уравнении, дискриминанте квадратного уравнения, формулах корней квадратного уравнения, теореме Виета; о числовых неравенствах, неравенстве с одной переменной, модуле действительного числа.
; о полном, приведенном, неполном квадратном уравнении, дискриминанте квадратного уравнения, формулах корней квадратного уравнения, теореме Виета; о числовых неравенствах, неравенстве с одной переменной, модуле действительного числа.
Формирование умений деления многочлена на многочлен с остатком, разложения многочлена на множители, сокращения дробей, приведения алгебраических дробей к общему знаменателю; построения графиков функций у = ах2, у = 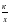 ,
, 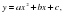
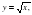 описание их свойств; решить приведенное квадратное уравнение, применяя обратную теорему Виета; исследования функции на монотонность, применения приближенных вычислений.
описание их свойств; решить приведенное квадратное уравнение, применяя обратную теорему Виета; исследования функции на монотонность, применения приближенных вычислений.
Целью изучения курса геометрии в 8 классе являются систематическое изучение свойств фигур на плоскости, формирование пространственных представлений, развитие логического мышления и подготовка аппарата, необходимого для изучения смежных дисциплин (физика, черчение и т.д.) и курса стереометрии в старших классах.
Задачи курса геометрии: систематизировать сведения о четырёхугольниках; сформировать представления о фигурах, симметричных относительно точки и прямой; сформировать понятие площади многоугольника; развить умение вычислять площади фигур; сформировать понятие подобных треугольников; выработать умение применять признаки подобия в процессе доказательства теорем и решении задач; сформировать навыки решения прямоугольных треугольников; расширить сведения об окружности.
В курсе геометрии 8-го класса продолжается решение задач на признаки равенства треугольников, но в совокупности с применением новых теоретических фактов. Теорема о сумме углов выпуклого многоугольника позволяет расширить класс задач. Формируются практические навыки вычисления площадей многоугольников в ходе решения задач. Особое внимание уделяется применению подобия треугольников к доказательствам теорем и решению задач. Вводятся первые знания о синусе, косинусе и тангенсе острого угла прямоугольного треугольника. Систематизируются сведения об окружности и её свойствах, вписанной и описанной окружностях. Серьезное внимание уделяется формированию умений рассуждать, выполнять простые доказательства, давать обоснования выполняемых действий.
При изучении курса геометрии решению задач уделяется большое внимание. Все новые понятия, теоремы, свойства геометрических фигур, способы рассуждений усваиваться в процессе решения задач.
Для изучения алгебры в 7-11 классах выбрана содержательная линия А.Г.Мордковича, а для изучения геометрии выбрана содержательная линия Л.С.Атанасяна, рассчитанные на 5 лет обучения. В восьмом классе реализуется второй год обучения. Рабочая программа ориентирована на использование учебников «Алгебра (в 2-х частях). Ч. 1: Учебник. 7 класс» / А.Г. Мордкович - 17-е изд., доп. – М.: Мнемозина, 2013 г. и задачнику «Алгебра (в 2-х частях). Ч. 2: Задачник. 7 класс» А.Г. Мордковичи др. – 17-е изд., стер. – М.: Мнемозина, 2013 г. и геометрия. 7 – 9 классы: учебник для общеобразовательных учреждений / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев, Э.Г. Позняк, И.И. Юдина. – М.: Просвещение, 2014.
Учебники и пособия под редакцией А.Г. Мордковича и Л.С. Атанасяна входят в федеральный перечень учебников и соответствует требованиям федерального компонента государственного образовательного стандарта общего образования.
Отличительными особенностями изучения алгебры по данному УМК являются рациональное сочетание четкости и доступности изложения, приоритетность функционально-графической линии, наличие большого числа примеров с подробными решениями. Практические задания к курсу содержатся во второй его части – задачнике.
Из основных содержательно-методических линий школьного курса алгебры приоритетной в программе является функционально-графическая линия. Это выражается прежде всего в том, что, какой бы класс функций, уравнений, выражений ни изучался, построение материала практически всегда осуществляется по жесткой схеме: функция — уравнения — преобразования.
Математические модели напрямую связаны с функциями, поэтому функции становятся ведущей идеей курса алгебры практически во всех. Реализуемая концепция изучения функций существенно отличается от традиционной. Методология концепции заключается в следующем: каждый год обучения ориентирован на конкретную модель реальной действительности, а именно в 8 классе изучается квадратичная функция, которая представляет модель равноускоренных процессов.
Отличительными особенностями изучения курса геометрии по данному УМК являются наглядность и строгая логика изложения материала. Увеличивается теоретическая значимость изучаемого материала, расширяются внутренние логические связи курса, повышается роль дедукции, степень абстрактности изучаемого материала. Учащиеся овладевают приемами аналитико-синтетической деятельности при доказательстве теорем и решении задач. Изложение материала характеризуется постоянным обращением к наглядности, использованием рисунков и чертежей на всех этапах обучения и развитием геометрической интуиции на этой основе. Целенаправленное обращение к примерам из практики развивает умения учащихся вычленять геометрические факты, формы и отношения в предметах и явлениях действительности, использовать язык геометрии для их описания. Рабочие тетради предназначены для работы учащихся на уроках и самостоятельно. Задания в них включают большое количество чертежей, помогают легко и быстро усвоить материал, способствуют осознанию учащимися логики рассуждений и усвоению различных методов решения задач.
Федеральный базисный учебный план для образовательных учреждений Российской Федерации предусматривает изучение математики в VII классе – 175 часов из расчета 5 ч в неделю (3 часа алгебры, 2 часа геометрии) за счет вариативной части Базисного плана увеличено учебное время до 6 уроков в неделю (4 часа алгебры, 2 часа геометрии), в том числе для проведения контрольных работ по алгебре 9 часов, по геометрии 5 часов, итоговая контрольная работа(переводной экзамен) в формате ГИА по математике.
Для изучения курсов алгебры и геометрии 8 класса выбран II вариант тематического планирования и программа составлена на 210 учебных часов и рассчитана на весь год обучения. Рекомендуется классно-урочная система с использованием различных технологий, форм, методов обучения.
В рабочую программу внесены незначительные изменения в количестве часов на изучение тем (модулей). Сравнительная таблица приведена ниже.
| № | Тема | Количество часов в примерной программе | Количество часов в рабочей программе |
| 1. | Повторение | - | 4 часа |
| 2. | Алгебраические дроби | 29 часов | 29 часов |
| 3. | Повторение | - | 2 часа |
| 4. | Четырехугольники | 14 часов | 14 часов |
| 5. | Функция у=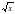 . Свойства квадратного корня . Свойства квадратного корня | 25 часов | 25 часов |
| 6. | Площадь | 14 часов | 14 часов |
| 7. | Квадратичная функция. Функция 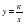 | 24 часа | 24 часа |
| 8. | Подобие треугольников | 19 часов | 20 часов |
| 9. | Квадратные уравнения | 24 часа | 24 часа |
| 10. | Окружность | 17 часов | 16 часов |
| 11. | Неравенства | 18 часов | 18 часов |
| 12. | Обобщающее повторение по геометрии | 4 часа | 4 часа |
| 13. | Обобщающее повторение по алгебре | 15 часов | 16 часов |
Формы и методы, используемые в преподавании
Основной формой организации учебно-воспитательной работы является урок. Данная программа предусматривает проведение следующих типов уроков:
Предполагаются совместные усилия учителя и учеников для решения общей проблемной познавательной задачи. На таком уроке используется демонстрационный материал на компьютере, разработанный учителем или учениками, мультимедийные продукты.
Вырабатываются у учащихся умения и навыки решения задач на уровне обязательной и возможной подготовке. Любой учащийся может использовать компьютерную информационную базу по методам решения различных задач, по свойствам элементарных функций и т.д.
Урок предполагает выполнение работ и заданий разного вида.
Предлагаются разные виды самостоятельных работ.
На основе игровой деятельности учащиеся познают новое, закрепляют изученное, отрабатывают различные учебные навыки.
Контроль знаний по пройденной теме.
При проведении уроков используются следующие методы:
объяснительно-иллюстративный (рассказ, беседа, лекция)
репродуктивный (выполнение типовых заданий)
практический (выполнение практических заданий и графических работ)
проблемно-поисковый(самостоятельное «открытие» новых знаний)
Используемые педагогические технологии
информационно-коммуникационные
личностно-ориентированного обучения
обучение с применением опорных схем
На уроках широко применяются ЭОР в качестве виртуальных лабораторий при проведении практических занятий, уроков введения новых знаний. В них заключен большой теоретический материал, много тренажеров, практических и исследовательских заданий, справочного материала. На любом из уроков возможно использование компьютерных устных упражнений, применение тренажера устного счета, что активизирует мыслительную деятельность учащихся, развивает вычислительные навыки, так как позволяет осуществить иной подход к изучаемой теме.
Использование компьютерных технологий в преподавании математики позволяет непрерывно менять формы работы на уроке, постоянно чередовать устные и письменные упражнения, осуществлять разные подходы к решению математических задач, а это постоянно создает и поддерживает интеллектуальное напряжение учащихся, формирует у них устойчивый интерес к изучению данного предмета.
II. Содержание тем учебного курса
Алгебра
1. Повторение
Основные цели:
обобщение и систематизация сведения курса алгебры 7 класса
формирование умений логически обосновывать суждения, выдвигать гипотезы и понимать необходимость их проверки;
формирование навыков ясно, точно и грамотно выражать свои мысли в устной и письменной речи, использовать различные языки математики (словесный, символический, графический) и свободно переходить с одного языка на другой для иллюстрации, интерпретации, аргументации и доказательства.
2. Алгебраические дроби
Основные понятия. Основное свойство алгебраической дроби. Сложение и вычитание алгебраических дробей с одинаковыми знаменателями. Сложение и вычитание алгебраических дробей с разными знаменателями. Умножение и деление алгебраических дробей. Возведение алгебраической дроби в степень. Преобразование рациональных выражений. Первые представления о рациональных уравнениях. Степень с отрицательным показателем
Основные цели:
формирование представлений об алгебраической дроби, области допустимых значений, основном свойстве алгебраической дроби, рациональном выражении;
формирование умений разложения многочлена на множители, сокращение дробей, применение основного свойства алгебраических дробей;
овладение умением упрощать выражения, складывать и вычитать алгебраические дроби с одинаковыми знаменателями;
овладение навыками составлять математические модели ситуации, описанной в условии задачи, решать задачи, выделяя три этапа математического моделирования.
3. Функция у=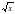 . Свойства квадратного корня
. Свойства квадратного корня
Рациональные числа. Понятие квадратного корня из неотрицательного числа. Иррациональные числа. Множество действительных чисел. Функция y = 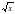 , её свойства и график. Свойства квадратных корней. Преобразование выражений, содержащих операцию извлечения квадратного корня. Модуль действительного числа, график функции
, её свойства и график. Свойства квадратных корней. Преобразование выражений, содержащих операцию извлечения квадратного корня. Модуль действительного числа, график функции 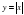 , формула
, формула 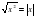 .
.
Основные цели:
формирование представлений о квадратном корне, квадратном корне из неотрицательного числа, о подкоренном выражении, об иррациональных числах, о кубическом корне из неотрицательного числа, о корне n-й степени из неотрицательного числа;
формирование умений извлечение квадратного корня и корня n-й степени из неотрицательного числа;
овладение умением строить график функции y = 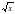 и описывать ее свойств;
и описывать ее свойств;
овладение навыками использовать алгоритм извлечения квадратного корня..
4 . Квадратичная функция. Функция 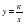 .
.
Функция у = кх2, ее свойства и график. Функция 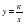 , ее свойства и график. Как построить график функции, если известен график функции y = f(x). Как построить график функции, если известен график функции y = f(x). Как построить график функции, если известен график функции y = f(x). Функция y = ax2 + bx + c, ее свойства и график. Графическое решение квадратных уравнений.
, ее свойства и график. Как построить график функции, если известен график функции y = f(x). Как построить график функции, если известен график функции y = f(x). Как построить график функции, если известен график функции y = f(x). Функция y = ax2 + bx + c, ее свойства и график. Графическое решение квадратных уравнений.
Основные цели:
формирование представлений о кусочно-заданных функциях, контрольных точках графика, параболе, оси симметрии параболы, асимптотах, оси симметрии гиперболы, об обратной пропорциональности, области значения функции, окрестности точки, о точках максимума и минимума;
формирование умений построения графика функций у = кх2, 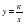 и описания их свойств;
и описания их свойств;
овладение умением использовать алгоритм построения графиков у = f(x + l), y = f (x) + m, у = f(x + l) + m;
овладение навыками преобразовывать функции параллельным переносом вправо (влево).
5. Квадратные уравнения
Основные понятия. Формулы корней квадратного уравнения. Рациональные уравнения. Рациональные уравнения как математические модели реальных ситуаций. Еще одна формула корней квадратного уравнения. Теорема Виета. Иррациональные уравнения.
Основные цели:
формирование представлений о квадратном уравнении, о старшем коэффициенте, втором коэффициенте, о свободном члене, о приведенном квадратном уравнении, полном квадратном уравнении, неполном квадратном уравнении, дискриминанте квадратного уравнения;
формирование умений решать квадратные уравнения;
овладение умением выводить формулы корней квадратного уравнения;
овладение навыками применять правила решения квадратного уравнения полного, неполного и приведенного.
6. Неравенства
Свойства числовых неравенств. Исследование функций на монотонность. Решение линейных неравенств. Решение квадратных неравенств. Приближенные значения действительных чисел. Стандартный вид положительного числа
Основные цели:
формирование представлений о числовых неравенствах, неравенстве с одной переменной, о свойстве числовых неравенств, о неравенствах с одной переменной, о свойстве числовых неравенств, о неравенствах одинакового смысла, неравенствах противоположного смысла, о среднем арифметическом и среднем геометрическом, о неравенстве Коши;
формирование умений решать линейные неравенства с одной переменной;
овладение умением решать системы линейных неравенств;
овладение навыками применять метод интервала для решения квадратичных неравенств.
7. Обобщающее повторение по алгебре
Алгебраические дроби. Квадратные уравнения. Неравенства. Функции и графики.
Основные цели:
обобщить и систематизировать курс алгебры за 8 класс, решая с учащимися задания повышенной сложности по всему курсу алгебры;
добиться понимания учащимися возможности использования приобретенных знаний и умений в практической деятельности и повседневной жизни;
сформировать умение интегрировать в личный опыт новую, в том числе самостоятельно полученную информацию.
Геометрия
1. Повторение
Основная цель - обобщение и систематизация сведения курса геометрии 7 класса
2. Четырехугольники
Многоугольник, выпуклый многоугольник, четырехугольник. Параллелограмм, его свойства и признаки. Трапеция. Прямоугольник, ромб, квадрат, их свойства. Осевая и центральная симметрии.
Основная цель - изучить наиболее важные виды четырехугольников — параллелограмм, прямоугольник, ромб, квадрат, трапецию; дать представление о фигурах, обладающих осевой или центральной симметрией.
Доказательства большинства теорем данной темы и решения многих задач проводятся с помощью признаков равенства треугольников, поэтому полезно их повторить, в начале изучения темы.
Осевая и центральная симметрии вводятся не как преобразование плоскости, а как свойства геометрических фигур, в частности четырехугольников. Рассмотрение этих понятий как движений плоскости состоится в 9 классе.
3. Площадь
Понятие площади многоугольника. Площади прямоугольника, параллелограмма, треугольника, трапеции. Теорема Пифагора.
Основная цель - расширить и углубить полученные в 5—6 классах представления обучающихся об измерении и вычислении площадей; вывести формулы площадей прямоугольника, параллелограмма, треугольника, трапеции; доказать одну из главных теорем геометрии — теорему Пифагора.
Вывод формул для вычисления площадей прямоугольника, параллелограмма, треугольника, трапеции основывается на двух основных свойствах площадей, которые принимаются исходя из наглядных представлений, а также на формуле площади квадрата, обоснование которой не является обязательным для обучающихся.
Нетрадиционной для школьного курса является теорема об отношении площадей треугольников, имеющих по равному углу. Она позволяет в дальнейшем дать простое доказательство признаков подобия треугольников. В этом состоит одно из преимуществ, обусловленных ранним введением понятия площади. Доказательство теоремы Пифагора основывается на свойствах площадей и формулах для площадей квадрата и прямоугольника. Доказывается также теорема, обратная теореме Пифагора.
4. Подобие треугольников
Подобные треугольники. Признаки подобия треугольников. Применение подобия к доказательству теорем и решению задач. Синус, косинус и тангенс острого угла прямоугольного треугольника.
Основная цель - ввести понятие подобных треугольников; рассмотреть признаки подобия треугольников и их применения; сделать первый шаг в освоении учащимися тригонометрического аппарата геометрии.
Определение подобных треугольников дается не на основе преобразования подобия, а через равенство углов и пропорциональность сходственных сторон.
Признаки подобия треугольников доказываются с помощью теоремы об отношении площадей треугольников, имеющих по равному углу.
На основе признаков подобия доказывается теорема о средней линии треугольника, утверждение о точке пересечения медиан треугольника, а также два утверждения о пропорциональных отрезках в прямоугольном треугольнике. Дается представление о методе подобия в задачах на построение.
В заключение темы вводятся элементы тригонометрии — синус, косинус и тангенс острого угла прямоугольного треугольника.
5. Окружность
Взаимное расположение прямой и окружности. Касательная к окружности, ее свойство и признак. Центральные и вписанные углы. Четыре замечательные точки треугольника. Вписанная и описанная окружности.
Основная цель - расширить сведения об окружности, полученные учащимися в 7 классе; изучить новые факты, связанные с окружностью; познакомить обучающихся с четырьмя замечательными точками треугольника.
В данной теме вводится много новых понятий и рассматривается много утверждений, связанных с окружностью. Для их усвоения следует уделить большое внимание решению задач.
Утверждения о точке пересечения биссектрис треугольника и точке пересечения серединных перпендикуляров к сторонам треугольника выводятся как следствия из теорем о свойствах биссектрисы угла и серединного перпендикуляра к отрезку. Теорема о точке пересечения высот треугольника (или их продолжений) доказывается с помощью утверждения о точке пересечения серединных перпендикуляров.
Наряду с теоремами об окружностях, вписанной в треугольник и описанной около него, рассматриваются свойство сторон описанного четырехугольника и свойство углов вписанного четырехугольника.
6. Обобщающее повторение по геометрии
Основная цель - повторение, обобщение и систематизация знаний, умений и навыков за курс геометрии 8 класса.
III. Календарно-тематическое планирование
| № | Дата | Тема урока | Материал учебника | На дом | Приме-чания |
| по плану | факт |
| I триместр, 9 недель – 54 часа |
| 1. | Повторение | 4 часа |
|
| 02.09 |
| Степень с натуральным показателем. Одночлены |
| дидак. матер. |
|
| 03.09 |
| Разложение многочлена на множители. Формулы сокращенного умножения |
| дидак. матер. |
|
| 04.09 |
| Функции и графики |
| дидак. матер. |
|
| 05.09 |
| Решение уравнений и систем уравнений |
| дидак. матер. |
|
| 2. | Алгебраические дроби | 29 часов |
|
| 06.09 |
| Алгебраические дроби. Основные понятия | §1 | §1, № 1.3 (г), 1.5 (в), 1.9 (б, в), 1.12 (а, б), 1.20 (б, г), 1.25 (а, б) |
|
| 08.09 |
|
|
| 09.09 |
| Основное свойство алгебраической дроби | §2 | §2, № 2.1 (б, в), 2.4 (б, в), 2.7 (б, г), 2.11, 2.19, 2.23 (б, в), 2.30 (а, г), 2.34 (б), 2.46 |
|
| 10.09 |
|
|
| 11.09 |
|
|
| 12.09 |
|
|
| 13.09 |
| Сложение и вычитание алгебраических дробей с одинаковыми знаменателями
| §3 | §3, № 3.2 (б, г), 3.7 (б, г), 3.10 (б, в), 3.13 (а, г), 3.15 (б), 3.16 (в, г), 3.19 (б), 3.22 |
|
| 15.09 |
|
|
| 16.09 |
|
|
| 17.09 |
| Сложение и вычитание алгебраических дробей с разными знаменателями | §4 | §4, № 4.4 (в, г), 4.7 (а, г), 4.18 (б, в), 4.18 (б, в), 4.19 (в), 4.23 (а), 4.30 (б, г), 4.35 |
|
| 18.09 |
|
|
| 19.09 |
|
|
| 20.09 |
|
|
| 22.09 |
|
|
| 23.09 |
| Контрольная работа № 1 «Сложение и вычитание алгебраических дробей» |
|
|
|
| 24.09 |
| Умножение и деление алгебраических дробей. Возведение дроби в степень | §5 | §5, № 5.4 (в), 5.7 (а), 5.12 (г), 5.17 (б), 5.18 (в), 5.21 (в), 5.28 (б), 5.36 (г), 5.39 (а) |
|
| 25.09 |
|
|
| 26.09 |
|
|
| 27.09 |
|
|
| 29.09 |
| Преобразование рациональных выражений |
§6 | §6, № 6.2 (в, г), 6.4 (а, б), 6.5 (г), 6.6 (в), 6.7 (б, в), 6.9 (в, г) |
|
| 30.09 |
|
|
| 01.10 |
|
|
| 02.10 |
| Первые представления о рациональных уравнениях | §7 | §7, № 7.3, 7.6 (г), 7.7 (б), 7.10 (б, в), 7.11 (а, б), 7.13 (в, г), 7.23 |
|
| 03.10 |
|
|
| 04.10 |
|
|
| 06.10 |
| Степень с отрицательным показателем | §8 | §8, № 8.1 (в, г), 8.3 (а, б), 8.6 (б, г), 8.8 |
|
| 07.10 |
|
|
| 08.10 |
|
|
| 09.10 |
| Контрольная работа № 2 «Умножение и деление алгебраических дробей» |
|
|
|
| 3. | Повторение | 2 часа |
|
| 10.10 |
| Повторение курса геометрии за 7 класс |
| Повторить признаки равенства треугольников, прямоугольных треугольников, задачи на построение |
|
| 11.10 |
|
| Задачи на повторение материала 7 класса |
|
| 4. | Четырехугольники | 14 часов |
|
| 13.10 |
| Многоугольники | п. 40-42 | п. 40-42, вопросы 1-5, задачи 364 (а, б), 365 (а, б, г), 368 из учебника, 1—2 из рабочей тетради |
|
| 14.10 |
| Задачи 366, 369, 370 из учебника, 7 из рабочей тетради |
|
| 15.10 |
| Параллелограмм | п. 43 | п. 43, вопросы 6—8, задачи 371 (а), 372 (в), 376 (в, г) из учебника, 10 из рабочей тетради |
|
| 16.10 |
| Признаки параллелограмма | п. 44 | п. 44, вопрос 9, задачи 383, 373, 378 (устно) из учебника, 12 из рабочей тетради |
|
| 17.10 |
| Решение задач по теме «Параллелограмм» | п. 43-44 | Задачи 375, 380, 384 (устно), 14 из РТ |
|
| 18.10 |
| Трапеция | п. 45 | п. 45, вопросы 10—11, задачи 386, 387, 390 из учебника, 17 из рабочей тетради |
|
| 20.10 |
| Теорема Фалеса | п. 45 | п. 45, вопросы 10—11, задачи 388, 391, 392 |
|
| 21.10 |
| Задачи на построение |
| прочитать решения задач 396, 393 (б, в); задачи 394,398 |
|
| 22.10 |
| Прямоугольник | п. 46 | п. 46, вопросы 12-13, задачи 399, 401 (а), 404 из учебника, 22 из рабочей тетради |
|
| 23.10 |
| Ромб. Квадрат | п. 47 | п. 47, вопросы 14-15, задачи 405, 409,411 из учебника |
|
| 24.10 |
| Решение задач по теме «Прямоугольник. Ромб. Квадрат» | п. 46-47 | вопросы 16—20, задачи 415 (б), 413 (а), 410 из учебника |
|
| 25.10 |
| Осевая и центральная симметрии | п. 48 | задания на карточках |
|
| 27.10 |
| Решение задач | п. 40-48 | задания на карточках |
|
| 28.10 |
| Контрольная работа № 3 «Четырехугольники» |
|
|
|
| 5. | Функция у=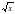 . Свойства квадратного корня . Свойства квадратного корня | 25 часов |
|
| 29.10 |
| Рациональные числа | §9 | §9, № 9.2, 9.4, 9.7, 9.9, 9.10 (б, г), 9.12 |
|
| 30.10 |
|
|
| 31.10 |
| Понятие квадратного корня из неотрицательного числа | §10 | §10, № 10.2, 10.5, 10.25 |
|
| 01.11 |
| §10 | §10, № 10.8 (б, в), 10.10, 10.15, 10.28 (г) |
|
| 10.11 |
|
|
| II триместр, 12 недель и 4 дня – 76 часов |
| 11.11 |
| Иррациональные числа | §11 | §11, № 11.13, 11.17, 11.2 (а, б), 11.4, 11.9 |
|
| 12.11 |
|
|
| 13.11 |
| Множество действительных чисел | §12 | §12, № 12.2, 12.9, 12.11, 12.15, 12.17 |
|
| 14.11 |
|
|
| 15.11 |
| Функция 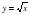 её свойства и график её свойства и график | §13 | §13,№13.2, 13.5(в, г), 13.6 (а, б), 13.9 (б, в), 13.11 (а, г), 13.15 (а) |
|
| 17.11 |
|
|
| 18.11 |
|
|
| 19.11 |
| Свойства квадратных корней | §14 | §14, № 14.2 (б, г), 14.3 (в, г), 14.5 (а, б), 14.7 (г), 14.10 (в) |
|
| 20.11 |
|
|
| 21.11 |
|
|
| 22.11 |
| Преобразование выражений, содержащих операцию извлечения квадратного корня | §15 | §15, № 15.3 (б, г), 15.15 (в), 15.26 (г), 15.38 (а), 15.42 (а, в), 15.46 (б, в), 15.52 (а, б), 15.53 (в), 15.64 (г) |
|
| 24.11 |
|
|
| 25.11 |
|
|
| 26.11 |
|
|
| 27.11 |
|
|
| 28.11 |
| Контрольная работа № 4 «Функция у=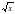 . . |
|
|
|
| 29.11 |
| Модуль действительного числа | §16 | §16, № 16.3 (б, г), 16.7 (в, г), 16.9, 16.16 (в), 16.20, 16.24 (в, г), 16.30 (б), 16.35 |
|
| 01.12 |
|
|
| 02.12 |
|
|
| 03.12 |
|
|
| 6. | Площадь | 14 часов |
|
| 04.12 |
| Площадь многоугольника | п. 49 | п. 49,вопросы 1-2, задачи 448, 449 (б), 450 (б), 446 из учебника |
|
| 05.12 |
| Площадь прямоугольника | п. 51 | п. 51, вопрос 3, задачи 454-456 из учебника и 32 из рабочей тетради
|
|
| 06.12 |
| Площадь параллелограмма | п. 52 | п. 52, вопрос 4, задачи 459 (в, г),460, 464 (а), 462 из учебника
|
|
| 08.12 |
| Площадь треугольника | п. 53 | п. 53, вопрос 5, зада- чи 468 (в, г), 473, 469 и 37 (РТ) |
|
| 09.12 |
| п. 53, вопрос 6, за- дачи 479 (а), 476 (а), 477 и 41(РТ) |
|
| 10.12 |
| Площадь трапеции | п. 54 | п. 54, вопрос 7, зада- чи 480 (б, в), 481,478, 476 (б) из учебника, повторить формулы площадей четыреху-гольников и треугольников |
|
| 11.12 |
| Решение задач на вычисление площадей фигур | п. 49-54 | задачи 466, 467 из учебника и 44 (РТ) |
|
| 12.12 |
| домашняя разноу-ровневая самостоя-тельная работа |
|
| 13.12 |
| Теорема Пифагора | п. 55 | п. 55, вопрос 8, задачи 483 (в, г), 484 (в, г, д), 486 (в) из учебника и 47 (РТ) |
|
| 15.12 |
| Теорема, обратная теореме Пифагора | п. 56 | п. 56, вопросы 9-10, задачи 498 (г-е), 499 (б), 488 и 49 (РТ) |
|
| 16.12 |
| Решение задач по теме «Теорема Пифагора» | п. 55-56 | задачи 489 (а, в), 491 (а), 493 и 50 (РТ) |
|
| 17.12 |
| Формула Герона | п. 57 | задачи 495 (б), 494, 490 (а), 524 (устно) |
|
| 18.12 |
| Решение задач | п. 49-56 | задачи 490 (в), 497, 503,518 из учебника |
|
| 19.12 |
| Контрольная работа № 5 «Площадь» |
|
|
|
| 7. | Квадратичная функция. Функция 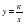 | 24 часа |
|
| 20.12 |
| Функция у = кх2, ее свойства и график | §17 | §17, № 17.5 (в, г), 17.13, 17.18 (в, г), 17.22 (б, в), 17.25, 17.28 (б, в), 17.49 |
|
| 22.12 |
|
|
| 23.12 |
|
|
| 24.12 |
|
|
| 25.12 |
| Функция 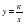 , ее свойства и график , ее свойства и график | §18 | §18, № 18.5, 18.10 (в, г), 18.13 (а), 18.14(г), 18.17 (б), 18.18 (в, г), 18.21, 18.25, 18.27. |
|
| 26.12 |
|
|
| 27.12 |
|
|
| 12.01 |
|
|
| 13.01 |
| Контрольная работа № 6 «Функции у = кх2 и 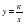 » » |
|
|
|
| 14.01 |
| Как построить график функции у = f(x + l), если известен график функции y = f(x) | §19 | §19, № 19.6, 19.7 (в, г), 19.8 (а, б), 19.9 (в, г), 19.12,19.14, 19.25, 19.36 (в), 19.39 (б) |
|
| 15.01 |
|
|
| 16.01 |
|
|
| 17.01 |
| Как построить график функции y = f(x) + m, если известен график функции y = f(x) | §20 | §20, № 20.6, 20.7 (в, г), 20.8 (б),20.9 (в, г), 20.10 (а, б), 20.12 (в), 20.14 (в, г), 20.22 |
|
| 19.01 |
|
|
| 20.01 |
| Как построить график функции y = f(x+1) + m, если известен график функции y = f(x) | §21 | §21, № 21.3 (в, г), 21.4 (а, б), 21.6, 21.12 (в, г), 21.14 (а, б), 21.17, 21.23,21.25 (б) |
|
| 21.01 |
|
|
| 22.01 |
|
|
| 23.01 |
| Функция y = ax2 + bx + c, ее свойства и график | §22 | §22, № 22.6 (в, г), 22.10 (а, б), 22.12 (г), 22.14, 22.21 (а, б), 22.25, 22.29(б), 22.46 |
|
| 24.01 |
|
|
| 26.01 |
|
|
| 27.01 |
|
|
| 28.01 |
| Графическое решение квадратных уравнений | §23 | §23, № 23.3 (в, г), 23.7 (а, б), 23.8 (г) |
|
| 29.01 |
|
|
| 30.01 |
| Контрольная работа № 7 «Квадратичная функция» |
|
|
|
| 8. | Подобие треугольников | 20 часов |
|
| 31.01 |
| Пропорциональные отрезки. Определение подобных треугольников | п.58-59 | п. 59, вопросы 1-3, задачи 534 (а, б), 536 (а), 538, 542 из учебника и 53 из РТ |
|
| 02.02 |
| Отношение площадей подобных треугольников | п. 60 | п. 60, вопрос 4, зада- чи 543, 544, 546, 549 из учебника |
|
| 03.02 |
| Первый признак подобия треугольников | п. 61 | п. 61, вопрос 5, задачи 550, 551 (б), 553, 555 (б) из учебника |
|
| 04.02 |
| Решение задач на применение первого признака подобия треугольников | п. 61 | п. 61, вопрос 5, зада- чи 552 (а, б), 556, 557 (в), 558 из учебника |
|
| 05.02 |
| Второй и третий признаки подобия треугольников | п. 62-63 | п. 62-63, вопросы 6—7, задачи 559—561 из учебника |
|
| 06.02 |
| Решение задач на применение признаков подобия треугольников | п. 61-63 | задачи 562, 563, 604, 605 из учебника |
|
| 07.02 |
| Решение задач | п. 59-63 | задачи на применение признаков подобия треугольников |
|
| 09.02 |
| Контрольная работа № 8 «Признаки подобия треугольников»
|
|
|
|
| 10.02 |
| Средняя линия треугольника | п. 64 | п. 64, вопросы 8—9, задачи 570, 571 из учебника и 63 (РТ) |
|
| 11.02 |
| Свойство медиан треугольника | п. 64 | задачи 568, 569 и 64, 65 (РТ) |
|
| 12.02 |
| Пропорциональные отрезки в прямоугольном треугольнике | п. 65 | п. 65, вопросы 10-11, задачи 572 (а, в, д), 573, 574 (б) |
|
| 13.02 |
| п. 65, задачи 575, 577, 579, 578(устно) |
|
| 14.02 |
| Измерительные работы на местности | п. 66 | п. 66, вопрос 13, задачи 580, 581 |
|
| 16.02 |
| Практические приложения подобия треугольников | п. 67 | п. 67, задачи 585 (б), 587,588,590 |
|
| 17.02 |
| задачи 606, 607, 628, 629 из учебника |
|
| 18.02 |
| Синус, косинус и тангенс острого угла в прямоугольном треугольнике | п. 68 | п. 68, вопросы 15-17, задачи 73 из рабочей тетради и 591 (в, г), 592 (б, г, е), 593 (в, г) из учебника |
|
| 19.02 |
| Значения синуса, косинуса и тангенса для углов, равных 30°, 45° и 60° | п. 69 | п. 69, вопрос 18, задачи 76 из рабочей тетради и 595, 597, 598 из учебника |
|
| 24.02 |
| Соотношения между сторонами и углами в треугольнике | п. 63-67 | повторить п. 63-67, задачи 77(РТ) и 601, 602 |
|
| III триместр, 13 недель и 2 дня – 80 часов |
| 25.02 |
| Решение задач | п. 63-67 | решить три-четыре задачи (620, 622, 623, 625) |
|
| 26.02 |
| Контрольная работа № 9 «Применение теории о подобии треугольников при решении задач» |
|
|
|
| 9. | Квадратные уравнения | 24 часа |
|
| 27.02 |
| Основные понятия | §24 | §24, № 24.6, 24.8, 24.10 (в), 24.12,24.32, 24.29, 24.22 (г) |
|
| 28.02 |
|
|
| 02.03 |
| Формулы корней квадратных уравнений | §25 | §25, № 25.10 (а, б), 25.17 (в, г), 25.25, 25.29, 25.33, 25.20 (а, б), 25.37 (в, г) |
|
| 03.03 |
|
|
| 04.03 |
|
|
| 05.03 |
| Рациональные уравнения | §26 | §26, № 26.4 (б), 26.6 (б, г), 26.8 (а), 26.11 (в, г), 26.13,26.15 (б), 26.17 (г), 26.23 (в, г) |
|
| 06.03 |
|
|
| 07.03 |
|
|
| 09.03 |
|
|
| 10.03 |
| Контрольная работа № 10 «Квадратные уравнения» |
|
|
|
| 11.03 |
| Рациональные уравнения как математические модели реальных ситуаций
| §27 | §27, № 272, 27.9, 27.15, 27.24, 27.28, 27.30, 27.34, 27.41, 27.45 |
|
| 12.03 |
|
|
| 13.03 |
|
|
| 14.03 |
|
|
| 16.03 |
| Еще одна формула корней квадратного уравнения
| §28 | §28, № 28.2 (в, г), 28.3 (а, б), 28.4 (в, г), 28.8, 28.12, 28.25 |
|
| 17.03 |
|
|
| 18.03 |
| Теорема Виета | §29 | §29, № 29.3 (в, г), 29.14, 29.40, 29.46, 29.8 (а, б), 29.22 (б) |
|
| 19.03 |
|
|
| 20.03 |
|
|
| 21.03 |
| Контрольная работа № 11 «Решение уравнений» |
|
|
|
| 23.03 |
| Иррациональные уравнения | §30 | §30, № 30.3 (в), 30.5 (в, г), 30.10 (а), 30.13 (в, г), 30.17 (а), 30.19 (в, г), 30.21 (а, б) |
|
| 24.03 |
|
|
| 25.03 |
|
|
| 26.03 |
|
|
| 10. | Окружность | 16 часов |
|
| 27.03 |
| Взаимное расположение прямой и окружности | п. 68 | п. 68, вопросы 1-2, задачи 631 (в, г), 632, 633 из учебника |
|
| 28.03 |
| Касательная к окружности | п. 69 | п. 69, вопросы 3—7, задачи 83 из рабочей тетради и 634, 636 |
|
| 30.03 |
|
| задачи 641, 643, 645 |
|
| 31.03 |
| Градусная мера дуги окружности | п. 70 | п. 70, вопросы 8—10, задачи 649 (б, г), 650 (б), 651 (б), 652 |
|
| 01.04 |
| Теорема о вписанном угле | п. 71 | п. 71, вопросы 11—13, задачи 654 (б), 655, 657, 659 из учебника |
|
| 02.04 |
| Теорема об отрезках пересекающихся хорд | п. 71 | п. 71, вопрос 14, задачи 660, 666 (б, в), 668, 671 (б) из учебника |
|
| 03.04 |
| Решение задач по теме «Центральные и вписанные углы» | п. 71 | задачи 91 из рабочей тетради и 661, 663, 673 из учебника |
|
| 04.04 |
| Свойство биссектрисы угла | п. 72 | п. 72, вопросы 15-16, задачи 675, 676 (б), 677, 678 (б) |
|
| 06.04 |
| Серединный перпендикуляр | п. 72 | п. 72, вопросы 17-19, задачи 102 (РТ) и 679 (б), 680 (б), 681 |
|
| 07.04 |
| Теорема о точке пересечения высот треугольника | п. 72 | домашняя разноуровневая самостоятельная работа |
|
| 13.04 |
| Вписанная окружность | п. 74 | п. 74, вопросы 21—22, задачи 689, 693 (б), 692, 694 из учебника |
|
| 14.04 |
| Свойство описанного четырехугольника | п. 74 | п. 74, вопрос 23, задачи 695, 699-701 |
|
| 15.04 |
| Описанная окружность | п. 75 | п. 75, задачи 702 (б), 705 (б), 707, 711 |
|
| 16.04 |
| Свойство вписанного четырехугольника
| п. 75 | задачи 709, 710, 731, 735 из учебника |
|
| 17.04 |
| Решение задач | п. 68-75 | задачи 726, 728, 722 |
|
| 18.04 |
| Контрольная работа № 12 «Окружность» |
|
|
|
| 11. | Неравенства | 18 часов |
|
| 20.04 |
| Свойства числовых неравенств | §31 | §31, № 31.14 (б, в), 31.18, 31.26 (а, б), 31.32 (а, б), 31.39 (б, г), 31.42 (в), 31.59 |
|
| 21.04 |
|
|
| 22.04 |
|
|
| 23.04 |
|
|
| 24.04 |
| Исследование функций на монотонность | §32 | §32, № 32.2, 32.9 (б), 32.3 (б, в), 32.6 (в, г), 32.7 (а, б), 32.8 (в, г) |
|
| 25.04 |
|
|
| 27.04 |
|
|
| 28.04 |
| Решение линейных неравенств | §33 | §33, № 33.2, 33.9 (в, г), 33.13, 33.20 (а, б), 33.25 (в, г), 33.26 (б) |
|
| 29.04 |
|
|
| 30.04 |
|
|
| 01.05 |
| Решение квадратных неравенств | §34 | §34, № 34.1 (в, г), 34.5 (а, б), 34.7 (в, г), 34.17 (а, б), 34.23 (в, г), 34.33 (в, г), 34.37 |
|
| 01.05 |
|
|
| 02.05 |
|
|
| 02.05 |
|
|
| 04.05 |
| Контрольная работа № 13 «Неравенства» |
|
|
|
| 05.05 |
| Приближенные значения действительных чисел | §35 | §35, № 35.1 (б, г), 35.2 (в),35.5, 35.7 (б), 35.9 (в, г),35.10 (а, б) |
|
| 06.05 |
|
|
| 07.05 |
| Стандартный вид положительного числа | §36 | §36, № 36.1 (в, г), 36.2 (а, б), 36.7 (в, г), 36.10 (б, в), 36.18 |
|
| 12. | Обобщающее повторение по геометрии | 4 часа |
|
| 08.05 |
| Повторение по теме «Четырехугольники» | Материалы ГИА | тематический тест |
|
| 09.05 |
| Повторение по теме «Площадь» | Материалы ГИА | тематический тест |
|
| 11.05 |
| Повторение по теме «Подобные треугольники» | Материалы ГИА | тематический тест |
|
| 12.05 |
| Повторение по теме «Окружность» |
|
|
|
| 13. | Обобщающее повторение по алгебре | 16 часов |
|
| 13.05 |
| Алгебраические дроби | Материалы ГИА | Тренировочный тест |
|
| 14.05 |
|
|
| 15.05 |
| Квадратные уравнения | Материалы ГИА | Тренировочный тест |
|
| 16.05 |
|
|
| 18.05 |
| Неравенства | Материалы ГИА | Тренировочный тест |
|
| 19.05 |
|
|
| 20.05 |
| Решение задач | Материалы ГИА | Тренировочный тест |
|
| 21.05 |
|
|
| 22.05 |
|
|
| 23.05 |
| Функции и графики | Материалы ГИА | Тренировочный тест |
|
| 25.05 |
|
|
| 26.05 |
| Обобщающий урок. Решение упражнений | Материалы ГИА | Тренировочный тест |
|
| 27.05 |
| Итоговая контрольная работа(экзаменационная работа в формате ГИА) |
|
|
|
| 28.05 |
|
|
|
|
| 29.05 |
| Решение упражнений. Анализ итоговой контрольной работы |
|
|
|
| 30.05 |
| Обобщение знаний по алгебре за курс 8 класса. |
|
|
|
IV. Формы и средства контроля
Входной контроль (контрольная работа)
Текущий контроль (фронтальный опрос, письменный опрос, самостоятельные работы, математические диктанты, контрольные работы, тесты)
Итоговый контроль (экзаменационная контрольная работа в формате ГИА)
V. Требования к уровню подготовки учащихся
В результате изучения математики ученик должен
знать/понимать
существо понятия математического доказательства; примеры доказательств;
существо понятия алгоритма; приводить примеры алгоритмов;
как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;
как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;
как потребности практики привели математическую науку к необходимости расширения понятия числа;
вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов;
смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации;
Алгебра
В результате изучения алгебры ученик должен
знать/понимать:
значение математической науки для решения задач, возникающих в теории и практике;
значение практики и вопросов, возникающих в самой математике для формирования и развития математической науки; историю развития понятия числа;
должен уметь:
выполнять арифметические действия, сочетая устные и письменные приемы; находить значения корня натуральной степени;
составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;
выполнять основные действия с многочленами и алгебраическими дробями; выполнять разложение многочленов на множители; выполнять тождественные выражения рациональных выражений;
применять свойства арифметических квадратных корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни;
решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним системы двух линейных уравнений и несложные нелинейные уравнения;
решать линейные и квадратные неравенства с одной переменной и их системы;
решать текстовые задачи алгебраическим методом, интерпретировать полученные результат, проводить отбор решений, исходя из формулировки задачи;
изображать числа точками на координатной прямой;
определять координаты точки плоскости, строить точки с заданными координатами; изображать множество решений линейного неравенства;
находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значения аргумента по значению функции, заданной графиком или таблицей;
определять свойства функции по ее графику; применять графические представления при решении уравнений, систем, неравенств;
описывать свойства изученных функций, строить их графики;
извлекать информацию, представленную в таблицах, на диаграммах, графиках; составлять таблицы, строить диаграммы и графики;
решать следующие жизненно-практические задачи:
самостоятельно приобретать и применять знания в различных ситуациях;
работать в группах;
аргументировать и отстаивать свою точку зрения;
уметь слушать других; извлекать учебную информацию на основе сопоставительного анализа объектов;
пользоваться предметным указателем энциклопедий и справочников для нахождения информации.
Геометрия
В результате изучения геометрии ученик должен
знать
уметь
пользоваться геометрическим языком для описания предметов окружающего мира;
распознавать геометрические фигуры, различать их взаимное расположение;
изображать геометрические фигуры, выполнять чертежи по условию задач, осуществлять преобразование фигур;
решать задачи на вычисление геометрических величин, применяя изученные свойства фигур и формулы;
решать геометрические задачи, опираясь на изученные свойства фигур и отношений между ними и применяя дополнительные построения, алгебраический аппарат и соображения симметрии;
проводить доказательные рассуждения при решении задач, используя известные теоремы и обнаруживая возможности для их использования;
решать простейшие планиметрические задачи в пространстве;
владеть алгоритмами решения основных задач на построение;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
описания реальных ситуаций на языке геометрии;
решения практических задач, связанных с нахождением геометрических величин (используя при необходимости справочники и технические средства);
построений геометрическими инструментами (линейка, угольник, циркуль, транспортир);
владения практическими навыками использования геометрических инструментов для изображения фигур, а также нахождения длин отрезков и величин углов.
VI. Перечень учебно-методического обеспечения
Методические и учебные пособия
Алгебра
Александрова Л.А. Алгебра. 8 класс. Самостоятельные работы для учащихся общеобразовательных учреждений - М.: Мнемозина, 2013
Александрова Л.А. Алгебра. 8 класс. Контрольные работы для учащихся общеобразовательных учреждений - М.: Мнемозина, 2013
Александрова Л.А. Алгебра. 8 класс. Тематические проверочные работы в новой форме для учащихся общеобразовательных учреждений - М.: Мнемозина, 2013
Ким Е.А. Алгебра. 8 кл.: Поурочные планы (по учебнику А.Г. Мордковича). -Волгоград: Учитель, 2006
Мордкович А.Г. Алгебра. 8 класс. Методическое пособие для учителя. - М.: Мнемозина, 2011
Руркин А.Н. Поурочные разработки по алгебре 8 класс. – М.: Вако, 2013
Тульчинская Е.Е. Алгебра. 8 класс. Блиц-опрос - М.: Мнемозина, 2012
Тульчинская Е.Е. Алгебра. 7-9 классы. Тесты для учащихся общеобразовательных учреждений - М.: Мнемозина, 2012
Геометрия
1. Алтынов П. И. Геометрия. Тесты. 7-9 классы: учеб.-мет. пособие - М.: Дрофа,2005.
2. Гаврилова Н.Ф. Поурочные разработки по геометрии. 8 класс. - М.: ВАКО, 2011
3. Зив Б.Г. Геометрия: дидактические материалы для 8 класса.- М.: Просвещение,2007.
4. Изучение геометрии в 7, 8, 9 классах: методические рекомендации: кн. для учителя / Л.С. Атанасян, В.Ф. Бутузов, Ю.А. Глазков и др. - М.: Просвещение, 2000 — 2008.
5. Мельникова Н. Б. Контрольные работы по геометрии, 8 класс: к учебнику Л. С. Атанасяна « Геометрия, 7-9» - М.: «Экзамен», 2009.
6. Самостоятельные и контрольные работы по алгебре и геометрии для 8 класса./ Ершова А. П., Голобородько В. В., Ершова А. С.— М.: Илекса, 2012
Оборудование и приборы
Аудиторная доска с магнитной поверхностью и набором приспособлений для крепления таблиц.
Комплект инструментов классных: линейка, угольник (300, 600), угольник (450), циркуль.
Учебно-методический комплекс «QOMO»
Индивидуальные ноутбуки
Дидактический материал
Карточки для проведения самостоятельных работ по всем темам курса.
Карточки для проведения контрольных работ.
Карточки для индивидуального опроса учащихся по всем темам курса.
Карточки для проведения тестирования по всем темам курса.
VII. Список литературы(основной и дополнительный)
Литература для ученика
Алгебра
Основная
Александрова Л. А. Алгебра 8 класс. Самостоятельные работы для общеобразовательных учреждений. - М.: Мнемозина, 2010-2012
Мордкович А. Г. Алгебра. 8 класс: учебник для общеобразовательных учреждений / А.Г. Мордкович. 14-е изд., стер. – М.: Мнемозина, 2012
Мордкович А. Г. Алгебра. 8 класс: задачник для общеобразовательных учреждений. А.Г. Мордкович. – 14-е изд., стер. – М.: Мнемозина, 2012
Тульчинская Е.Е. Алгебра 8 класс. Блиц опрос. Пособие для учащихся общеобразовательных учреждений. М.: Мнемозина, 2012
2)Дополнительная
Лысенко Ф.Ф. Тесты для промежуточной аттестации. 7-8 класс– Ростов–на-Дону: Легион-М, 2011
Мордкович А. Г., Тульчинская Е.Е.. Алгебра 7-9 классы. Тесты для учащихся общеобразовательных учреждений.- М.: Мнемозина, 2013
Панарина В.И. Алгебра. ГИА. Экспресс-диагностика. 8 класс. 208 диагностических варианта. – М.: Национальное образование, 2012
Пособия для учителя
Виноградова Л.В. Методика преподавания математики в средней школе: учеб.пособие. – Ростов-на-Дону: Феникс, 2005
Мордкович А.Г. Беседы с учителями математики: Учеб.-метод. пособие. – 2-е изд., доп. и перераб. – М.: ООО «Издательство Оникс», 2008
Программы. Математика. 5-6 классы. Алгебра. 7-9 классы. Алгебра и начала анализа. 10-11 классы / авт.-сост. Зубарева И.И., Мордкович А.Г. 2-е изд., испр. и доп. – М.: Мнемозина, 2009
Геометрия
Литература для ученика
1)Основная
1. Геометрия: рабочая тетрадь для 8 кл. /Л. С. Атанасян, В.Ф. Бутузов, Ю.А. Глазков, И.И. Юдина. – М.: Просвещение, 2009
2. Геометрия, учеб. для 7-9 кл./ [Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др.] – М.: Просвещение, 2010
3. Левитас Г.Г. Карточки для коррекции знаний по геометрии для 8-9 классов – М.: Илекса, 2003
2)Дополнительная
Ершова А.П., Голобородько В.В., Крижановский А.Ф. Тетрадь – конспект по геометрии для 8 класса. – М.: Илекса, 2008
Рабинович Е.М. Задачи и упражнения на готовых чертежах. 7-9 классы. Геометрия. – М.: Илекса, 2007
3. Черняк А.А. Геометрия. 7-11 классы. ЕГЭ шаг за шагом. - М.: Дрофа, 2011
Пособия для учителя
Геометрия. 7-11 классы: развернутое тематическое планирование. Базовый уровень. Линия Л.С.Атанасян / авт. – сост. Т.А.Салова. – Волгоград: Учитель, 2010
Программы общеобразовательных учреждений. Геометрия. 7-9 классы/состав.Т. А. Бурмистрова – М.: Просвещение, 2008
Рабинович Е.М. Задачи и упражнения на готовых чертежах. 7-9 классы. Геометрия. – М.: Илекса, 2007
Рабочие программы по геометрии: 7-11 классы / сост. Н.Ф.Гаврилова. – М.: Вако, 2011
Примерная программа общеобразовательных учреждений по геометрии 7–9 классы, к учебному комплексу для 7-9 классов, авторы Л.С. Атанасян, В.Ф. Бутузов, С.В. Кадомцев и др., составитель Т.А. Бурмистрова – М: «Просвещение», 2008 – М: «Просвещение», 2008. – с. 19-21.
Сборник нормативных документов.
Федеральный компонент государственных образовательных стандартов основного общего образования (приказ Минобрнауки от 05.03.2004г. № 1089).
Черняк А.А. Геометрия. 7-11 классы. ЕГЭ шаг за шагом. - М.: Дрофа, 2011
Электронные учебные пособия
Интерактивная математика. 5-9 класс. Электронное учебное пособие для основной школы. М., ООО «Дрофа», ООО «ДОС», 2002.
Мастер диагностики учащихся 7-9 классов. Зыкин В.Г.
Математика. Практикум. 5-11 классы. Электронное учебное издание. М., ООО «Дрофа», ООО «ДОС», 2004.


 Получите свидетельство
Получите свидетельство Вход
Вход


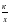 , гиперболе, перемещении графика по координатной плоскости, квадратичной функции
, гиперболе, перемещении графика по координатной плоскости, квадратичной функции 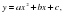 ; о квадратном корне из неотрицательного числа, о функции
; о квадратном корне из неотрицательного числа, о функции 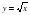 ; о полном, приведенном, неполном квадратном уравнении, дискриминанте квадратного уравнения, формулах корней квадратного уравнения, теореме Виета; о числовых неравенствах, неравенстве с одной переменной, модуле действительного числа.
; о полном, приведенном, неполном квадратном уравнении, дискриминанте квадратного уравнения, формулах корней квадратного уравнения, теореме Виета; о числовых неравенствах, неравенстве с одной переменной, модуле действительного числа.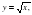 описание их свойств; решить приведенное квадратное уравнение, применяя обратную теорему Виета; исследования функции на монотонность, применения приближенных вычислений.
описание их свойств; решить приведенное квадратное уравнение, применяя обратную теорему Виета; исследования функции на монотонность, применения приближенных вычислений. 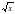 . Свойства квадратного корня
. Свойства квадратного корня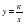
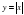 , формула
, формула 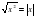 .
.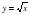 её свойства и график
её свойства и график








 Рабочая программа по математике для 8 класса (0.11 MB)
Рабочая программа по математике для 8 класса (0.11 MB)
 0
0 594
594 5
5 Нравится
0
Нравится
0


