Настоящая программа по алгебре для 8 класса составлена на основе федерального компонента государственного стандарта основного общего образования (приказ МОиН РФ от 05.03.2004г. № 1089), примерной программы для общеобразовательных учреждений по алгебре 7-9 классы к учебному комплексу для 7-9 классов (составители И.И.Зубарева, А.Г.Мордкович. – М.: Мнемозина, 2009).
Учебно-методический комплект по математике издательства «Мнемозина» (автор А.Г.Мордкович) соответствует государственному стандарту и является оптимальным комплектом, наиболее полно обеспечивающим реализацию основных содержательно-методических линий математики базовой школы. Новое издание этого комплекта является полным и доработанным в соответствии с требованиями нормативных документов, имеет завершенность учебной линии.
Рабочая программа конкретизирует содержание предметных тем образовательного стандарта и показывает распределение учебных часов по разделам курса. Согласно федеральному базисному учебному плану для образовательных учреждений Российской Федерации на изучение алгебры в 8 классе отводится 102 часа из расчёта 3 часа в неделю. Рабочая программа по алгебре для 8 класса рассчитана на 136 часов из расчёта 4 часа в неделю. Дополнительные часы используются для расширения знаний и умений по отдельным темам всех разделов курса.
В программу внесены изменения: увеличено количество часов на изучение некоторых тем. Сравнительная таблица приведена ниже.
Внесение данных изменений позволит охватить весь изучаемый материал по программе, повысить уровень обученности учащихся по предмету, а также более эффективно осуществить индивидуальный подход к обучающимся.
Понятие алгебраической дроби. Основное свойство алгебраической дроби. Сокращение алгебраических дробей.
Сложение и вычитание алгебраических дробей. Умножение и деление алгебраических дробей. Возведение алгебраической дроби в степень.
Рациональное выражение. Рациональное уравнение. Решение рациональных уравнений (первые представления).
Степень с отрицательным целым показателем.
Рациональные числа. Понятие квадратного корня из неотрицательного числа. Иррациональные числа. Множество действительных чисел.
Свойства квадратных корней. Преобразование выражений, содержащих операцию извлечения квадратного корня. Освобождение от иррациональности в знаменателе дроби. Модуль действительного числа. График функции у = \х\.
Квадратный трехчлен. Квадратичная функция, ее свойства и график. Понятие ограниченной функции. Построение и чтение графиков кусочных функций, составленных из функций у = С, у = kx + т, у = ах2, у = ах2+ Ьх + с, у = k/x, у = |х|.
Графическое решение квадратных уравнений.
Квадратное уравнение. Приведенное (неприведенное) квадратное уравнение. Полное (неполное) квадратное уравнение. Корень квадратного уравнения. Решение квадратного уравнения методом разложения на множители, методом выделения полного квадрата.
Дискриминант. Формулы корней квадратного уравнения. Параметр. Уравнение с параметром (начальные представления).
Алгоритм решения рационального уравнения. Биквадратное уравнение. Метод введения новой переменной.
Рациональные уравнения как математические модели реальных ситуаций.
Частные случаи формулы корней квадратного уравнения. Теорема Виета. Разложение квадратного трехчлена на линейные множители.
Иррациональное уравнение. Метод возведения в квадрат.
Свойства числовых неравенств.
Неравенство с переменной. Решение неравенств с переменной. Линейное неравенство. Равносильные неравенства. Равносильное преобразование неравенства.
Квадратное неравенство. Алгоритм решения квадратного неравенства.
Возрастающая функция. Убывающая функция. Исследование функций на монотонность (с использованием свойств числовых неравенств).
Приближенные значения действительных чисел, погрешность приближения, приближение по недостатку и избытку. Стандартный вид числа.
6. Случайные события и их вероятности
Критерии и нормы оценки знаний, умений и навыков обучающихся по алгебре. 1. Оценка письменных контрольных работ обучающихся по алгебре.
Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.
2. Оценка устных ответов обучающихся по алгебре.
б) за год – 8.
Количество лабораторных и других видов практических работ (указать, сколько и каких) - нет
1) Примерные программы основного общего образования по математике.
Вестник образования. №2, 2006г.
2)Сборник нормативных документов. Математика. Федеральный компонент государственного стандарта. Федеральный базисный план. Москва. Дрофа, 2007г.
3) Программно- методические материалы. Математика 5 – 11 классы.
Москва. Дрофа, 2002г.
Авторы: А. П. Ершова, В. В. Голобородько, А. С. Ершова.
Москва. Илекса. 2003г.
1) Математический энциклопедический словарь.
Москва. Советская энциклопедия, 1995.
Планирование составлено в соответствии Федерального компонента государственного стандарта основного общего образования и программы по математике для общеобразовательных учреждений
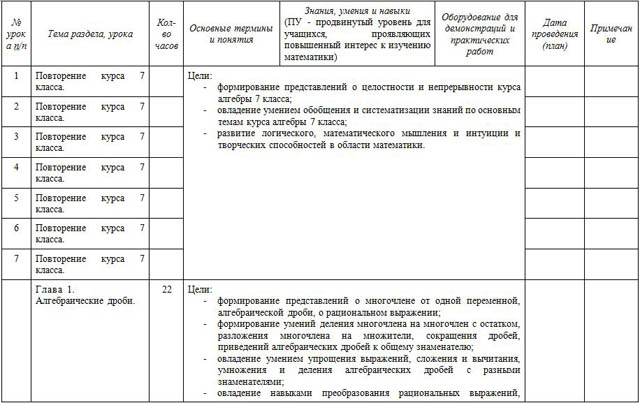
| № урока п/п | Тема раздела, урока | Кол-во часов | Основные термины и понятия | Знания, умения и навыки (ПУ - продвинутый уровень для учащихся, проявляющих повышенный интерес к изучению математики) | Оборудование для демонстраций и практических работ | Дата проведения (план) | Примечание |
| 1 | Повторение курса 7 класса. |
| Цели: формирование представлений о целостности и непрерывности курса алгебры 7 класса; овладение умением обобщения и систематизации знаний по основным темам курса алгебры 7 класса; развитие логического, математического мышления и интуиции и творческих способностей в области математики. |
|
|
| 2 | Повторение курса 7 класса. |
|
|
|
| 3 | Повторение курса 7 класса. |
|
|
|
| 4 | Повторение курса 7 класса. |
|
|
|
| 5 | Повторение курса 7 класса. |
|
|
|
| 6 | Повторение курса 7 класса. |
|
|
|
| 7 | Повторение курса 7 класса. |
|
|
|
|
| Глава 1. Алгебраические дроби. | 22 | Цели: формирование представлений о многочлене от одной переменной, алгебраической дроби, о рациональном выражении; формирование умений деления многочлена на многочлен с остатком, разложения многочлена на множители, сокращения дробей, приведений алгебраических дробей к общему знаменателю; овладение умением упрощения выражений, сложения и вычитания, умножения и деления алгебраических дробей с разными знаменателями; овладение навыками преобразования рациональных выражений, доказательства тождеств, решения рациональных уравнений способом освобождения от знаменателей с составлением математической модели реальной ситуации. |
| |
| 8 | § 1. Алгебраические дроби. Основные понятия. | 1 | Алгебраическая дробь, числитель, знаменатель дроби, область допустимых значений дроби. | Иметь представление о числителе, знаменателе алгебраической дроби, о значении дроби и о значении переменной. | Учебник, диск сопровождения учебника. |
|
|
| 9 | § 1. Алгебраические дроби. Основные понятия. | 1 |
| Уметь распознавать алгебраические дроби, находить множество допустимых значений переменной алгебраической дроби. (ПУ) Уметь составлять математическую модель ситуации, описанной в условии задачи; решать задачи, выделяя три этапа математического моделирования. | Учебник, слайды. |
|
|
| 10 | § 2. Основное свойство алгебраической дроби. | 1 | Основное свойство алгебраической дроби, сокращение дробей, приведение алгебраических дробей к общему знаменателю. | Иметь представление об основном свойстве алгебраической дроби, о сокращении дроби, о приведении дробей к общему знаменателю. (ПУ) Уметь раскладывать числитель и знаменатель дроби на простые множители. | Учебник, раздаточный материал, слайды. |
|
|
| 11 | § 2. Основное свойство алгебраической дроби. | 1 |
| Уметь применять основное свойство при преобразовании алгебраических дробей и их сокращении. (ПУ) Уметь раскладывать числитель и знаменатель дроби на простые множители. | Учебник, слайды, раздаточный материал. |
|
|
| 12 | § 2. Основное свойство алгебраической дроби. | 1 |
| Уметь применять основное свойство при преобразовании алгебраических дробей и их сокращении. (ПУ) Уметь раскладывать числитель и знаменатель дроби на простые множители. | Учебник, демонстрация на доске, раздаточный материал. |
|
|
| 13 | § 3. Сложение и вычитание алгебраических дробей с одинаковыми знаменателями. | 1 | Алгебраическая дробь, алгоритм сложения и вычитания алгебраических дробей с одинаковым знаменателем. | Иметь представление о сложении и вычитании дробей с одинаковыми знаменателями. (ПУ) Уметь доказывать, что при любом значении переменной дробь принимает положительное (отрицательное) значение. | Учебник. |
|
|
| 14 | § 4. Сложение и вычитание алгебраических дробей с разными знаменателями. | 1 | Упрощение выражений, сложение и вычитание дробей с разными знаменателями, наименьший общий знаменатель, правило приведения алгебраических дробей к общему знаменателю, дополнительный множитель, допустимые значения переменной. | Иметь представление о наименьшем общем знаменателе, о дополнительном множителе, о сложении и вычитании дробей с разными знаменателями. | Учебник, слайды. |
|
|
| 15 | § 4. Сложение и вычитание алгебраических дробей с разными знаменателями. | 1 | Знать алгоритм сложения и вычитания дробей с разными знаменателями. (ПУ) Уметь находить общий знаменатель нескольких дробей; доказывать тождества. | Учебник, раздаточный материал, слайды. |
|
|
| 16 | § 4. Сложение и вычитание алгебраических дробей с разными знаменателями. | 1 |
| Знать алгоритм сложения и вычитания дробей с разными знаменателями. Уметь находить общий знаменатель нескольких дробей. (ПУ) Уметь упрощать выражения, используя формулы сокращенного умножения. | Учебник, демонстрация на доске, слайды. |
|
|
| 17 | Контрольная работа №1 по теме «Сложение и вычитание алгебраических дробей». | 1 |
| Уметь обобщать и систематизировать знания и умения по данной теме. | Контрольно-измерительный дифференцированный материал. |
|
|
| 18 | § 5. Умножение и деление алгебраических дробей. Возведение алгебраической дроби в степень. | 1 | Умножение и деление алгебраических дробей, возведение алгебраических дробей в степень, преобразование выражений, содержащих алгебраические дроби. | Иметь представление об умножении и делении алгебраических дробей, возведении в степень. Знать правила сложения, вычитания, умножения и деления дробей. (ПУ) Уметь упрощать выражения наиболее рациональным способом. | Учебник, раздаточный материал, слайды. |
|
|
| 19 | § 5. Умножение и деление алгебраических дробей. Возведение алгебраической дроби в степень. | 1 |
| Уметь пользоваться алгоритмом умножения и деления дробей, возведения дроби в степень, упрощая выражение. (ПУ) Уметь применять формулы сокращенного умножения, доказывать тождества, формулировать выводы. | Учебник, слайды. |
|
|
| 20 | § 6. Преобразование рациональных выражений. | 1 | Преобразование рациональных выражений, рациональные выражения, доказательства тождеств. | Иметь представления о преобразовании рациональных выражений, используя все действия с алгебраическими дробями. (ПУ) Уметь находить и устранять причину возникающих затруднений. | Иллюстрация на доске, учебник, раздаточный материал. |
|
|
| 21 | § 6. Преобразование рациональных выражений. | 1 |
| Знать, как преобразовывать выражения, используя все действия с алгебраическими дробями. (ПУ) Уметь решать рациональные уравнения. | Учебник, раздаточный материал. |
|
|
| 22 | § 6. Преобразование рациональных выражений. | 1 |
| Уметь преобразовывать выражения, используя все действия с алгебраическими дробями. (ПУ) Уметь доказывать тождества, решать рациональные уравнения, задачи, выделяя три этапа математического моделирования. | Учебник, раздаточный материал, иллюстрация на доске. |
|
|
| 23 | § 7. Первые представления о решении рациональных уравнений. | 1 | Рациональные уравнения, способ освобождения от знаменателя, составление математической модели. | Иметь представление о рациональном уравнении, об освобождении от знаменателя при решении уравнения. (ПУ) Уметь решать рациональные уравнения, применяя формулы сокращенного умножения. | Иллюстрация на доске, учебник. |
|
|
| 24 | § 7. Первые представления о решении рациональных уравнений. | 1 |
| Иметь представление о составлении математической модели реальной ситуации. (ПУ) Уметь составлять и решать задачи, выделяя три этапа математического моделирования. | Иллюстрация на доске, учебник, раздаточный материал. |
|
|
| 25 | § 7. Первые представления о решении рациональных уравнений. | 1 |
| Знать, как решать рациональные уравнения и как составлять математические модели реальных ситуаций. (ПУ) Уметь решать рациональные уравнения, применяя формулы сокращенного умножения. | Раздаточный материал. |
|
|
| 26 | § 8. Степень с отрицательным целым показателем. | 1 | Степень с натуральным показателем, степень с отрицательным показателем, умножение, деление и возведение в степень степени числа. | Иметь представление о степени с натуральным и отрицательным показателем, об умножении, делении и возведении степени в степень. (ПУ) Выполнять более сложных преобразований выражений, содержащих степень с отрицательным показателем, уметь доказывать тождества. | Иллюстрация на доске, учебник, раздаточный материал. |
|
|
| 27 | § 8. Степень с отрицательным целым показателем. | 1 |
| Уметь упрощать выражения, используя степень с отрицательным показателем и свойства степени. | Учебник, раздаточный материал. |
|
|
| 28 | § 8. Степень с отрицательным целым показателем. | 1 |
| Уметь упрощать выражения, используя степень с отрицательным показателем и свойства степени. | Учебник, раздаточный материал. |
|
|
| 29 | Контрольная работа №2 по теме «Умножение и деление рациональных дробей. Степень с целым отрицательным показателем». | 1 |
| Уметь обобщать и систематизировать знания и умения по данной теме. | Контрольно-измерительный дифференцированный материал. |
|
|
|
| Глава 2. Функция y= √x. Свойства квадратного корня.
| 25 | Цели: формирование представлений о квадратном корне из неотрицательного числа, и функции у=√x; формирование умений построения графика функции у=√x и описания её свойств, использования алгоритма извлечения квадратного корня; овладение умением преобразования выражения, содержащего операцию извлечения квадратного корня, применяя свойства квадратных корней; овладение навыками решения уравнений, содержащих радикал. |
|
|
| 30 | § 9. Рациональные числа. | 1 | Множество рациональных чисел, знак принадлежности, знак включения, символы математического языка, бесконечные десятичные периодические дроби, период, чисто периодическая дробь, смешано периодическая дробь. | Знать понятие рационального числа, бесконечной десятичной периодической дроби. (ПУ) Уметь любое рациональное число записать в виде конечной десятичной дроби и наоборот. | Учебник, слайды. |
|
|
| 31 | § 9. Рациональные числа. | 1 |
| Знать понятие рационального числа, бесконечной десятичной периодической дроби. (ПУ) Уметь любое рациональное число записать в виде конечной десятичной дроби и наоборот. | Демонстрация на доске, раздаточный дифференцированный материал. |
|
|
| 32 | § 10. Понятие квадратного корня из неотрицательного числа. | 1 | Квадратный корень, квадратный корень из неотрицательного числа, подкоренное выражение, извлечение квадратного корня, иррациональные числа, кубический корень из неотрицательного числа, корень n-ой степени из неотрицательного числа. | Уметь извлекать квадратные корни из неотрицательного числа. | Учебник, демонстрация на доске. |
|
|
| 33 | § 10. Понятие квадратного корня из неотрицательного числа. | 1 |
| Уметь извлекать квадратные корни из неотрицательного числа. | Учебник, раздаточный дифференцированный материал. |
|
|
| 34 | § 10. Понятие квадратного корня из неотрицательного числа. | 1 |
| Уметь извлекать квадратные корни из неотрицательного числа.
| Учебник, демонстрация на доске, раздаточный материал. |
|
|
| 35 | §11. Иррациональные числа. | 1 | Иррациональные числа, бесконечные десятичная непериодическая дробь, иррациональные выражения. | Иметь представление о понятии иррационального числа. (ПУ) Уметь доказать иррациональность числа, объяснить изученные положения на самостоятельно подобранных примерах. | Учебник, слайды. |
|
|
| 36 | §11. Иррациональные числа. | 1 |
| Иметь представление о понятии иррационального числа. (ПУ) Уметь решать уравнения, корнем которого являются иррациональные числа. | Учебник, демонстрация на доске, раздаточный материал. |
|
|
| 37 | § 12. Множество действительных чисел. | 1 | Множество действительных чисел, сравнение действительных чисел, действия над действительными числами. | Знать о делимости целых чисел, о делении с остатком. Уметь решать задачи с целочисленным неизвестным. | Учебник, демонстрация на доске. |
|
|
| 38 | § 12. Множество действительных чисел. | 1 |
| Знать о делимости целых чисел, о делении с остатком. Уметь решать задачи с целочисленным неизвестным. | Учебник, раздаточный материал. |
|
|
| 39 | § 13. Функция у=√x, ее свойства и график. | 1 | Функция у=√x, ее свойства и график, функция, выпуклая вверх, функция, выпуклая вниз. | Уметь строить график функции у=√x, знать ее свойства. (ПУ) Умет читать график функции, решать графически уравнения и системы уравнений. | Учебник, демонстрация на доске. |
|
|
| 40 | § 13. Функция у=√x, ее свойства и график. | 1 |
| Уметь строить график функции у=√x, знать ее свойства. (ПУ) Умет читать график функции, решать графически уравнения и системы уравнений. | Учебник, раздаточный дифференцированный материал. |
|
|
| 41 | § 13. Функция у=√x, ее свойства и график. | 1 |
| Уметь строить график функции у=√x, знать ее свойства. (ПУ) Умет читать график функции, решать графически уравнения и системы уравнений. | Учебник, раздаточный дифференцированный материал. |
|
|
| 42 | § 14. Свойства квадратных корней. | 1 | Квадратный корень из произведения, квадратный корень из дроби, вычисление корней. | Знать свойства квадратных корней. Уметь применять свойства квадратного корня при нахождении значения выражения. (ПУ) Выполнять более сложные упрощения выражений наиболее рациональным способом. | Учебник, демонстрация на доске. |
|
|
| 43 | § 14. Свойства квадратных корней. | 1 |
| Уметь применять свойства квадратных корней для упрощения выражений и вычисления корней. (ПУ) Уметь вычислять значения квадратного корня, не используя таблицу квадратов чисел. | Учебник, раздаточный материал. |
|
|
| 44 | § 14. Свойства квадратных корней. | 1 |
| Уметь применять свойства квадратных корней для упрощения выражений и вычисления корней. (ПУ) Уметь вычислять значения квадратного корня, не используя таблицу квадратов чисел. | Учебник, раздаточный материал, слайды |
|
|
| 45 | § 15. Преобразование выражений, содержащих операцию извлечения квадратного корня. | 1 | Преобразование выражений, содержащих операцию извлечения квадратного корня, освобождение от иррациональности в знаменателе. | Иметь представление о преобразовании выражений, об извлечении квадратного корня и освобождении иррациональности в знаменателе. (ПУ) Уметь оценивать не извлекающиеся корни, находить их приближенное значение. | Учебник, слайды, раздаточный материал. |
|
|
| 46 | § 15. Преобразование выражений, содержащих операцию извлечения квадратного корня. | 1 |
| Знать о преобразовании выражений, об операциях извлечения квадратного корня и освобождении иррациональности в знаменателе. (ПУ) Уметь раскладывать на множители выражение способом группировки, используя определение и свойства квадратного корня. | Учебник, слайды, раздаточный материал. |
|
|
| 47 | § 15. Преобразование выражений, содержащих операцию извлечения квадратного корня. | 1 |
| Уметь выполнять преобразования, содержащие операцию извлечения корня, освобождаться лот иррациональности в знаменателе. (ПУ) Уметь раскладывать выражение на множители, используя формулы квадрата суммы и разности. | Учебник, демонстрация на доске, раздаточный материал. |
|
|
| 48 | § 15. Преобразование выражений, содержащих операцию извлечения квадратного корня. | 1 |
| Уметь выполнять преобразования, содержащие операцию извлечения корня, освобождаться лот иррациональности в знаменателе. (ПУ) Уметь раскладывать выражение на множители, используя формулы квадрата суммы и разности. | Учебник, демонстрация на доске. |
|
|
| 49 | § 15. Преобразование выражений, содержащих операцию извлечения квадратного корня. | 1 |
| Уметь выполнять преобразования, содержащие операцию извлечения корня, освобождаться лот иррациональности в знаменателе. (ПУ) Уметь сокращать дроби, раскладывая выражения на множители, освобождаться от иррациональности в знаменателе. | Учебник, раздаточный материал. |
|
|
| 50 | Контрольная работа №3 по теме «Квадратный корень. Функция у = √x, её свойства». | 1 |
| Уметь обобщать и систематизировать знания и умения по данной теме. | Контрольно-измерительный дифференцированный материал. |
|
|
| 51 | § 16. Модуль действительного числа. | 1 | Модуль действительного числа, свойства модулей, геометрический смысл модуля действительного числа, совокупность уравнений, тождество √a2=|a|. | Иметь представление об определении модуля действительного числа. Уметь применять свойства модуля. (ПУ) Уметь доказывать свойства модуля и решать модульные неравенства. | Учебник, демонстрация на доске. |
|
|
| 52 | § 16. Модуль действительного числа. | 1 |
| Иметь представление об определении модуля действительного числа. Уметь применять свойства модуля. (ПУ) Уметь доказывать свойства модуля и решать модульные неравенства. | Иллюстрация на доске, раздаточный материал. |
|
|
| 53 | § 16. Модуль действительного числа. | 1 |
| Иметь представление об определении модуля действительного числа. Уметь применять свойства модуля. (ПУ) Уметь доказывать свойства модуля и решать модульные неравенства. | Учебник, слайды, раздаточный материал. |
|
|
| 54 | § 16. Модуль действительного числа. | 1 |
| Иметь представление об определении модуля действительного числа. Уметь применять свойства модуля. (ПУ) Уметь доказывать свойства модуля и решать модульные неравенства. | Учебник, слайды, раздаточный материал. |
|
|
|
| Глава 3. Квадратичная функция. Функция y= k/x. | 24 | Цель: формирование представлений о функции у=кх2, о функции у=к/х, о гиперболе, о перемещении графика по координатной плоскости, о квадратичной функции у=ax2+bx+c; формирование умений построения графиков функции у=кх2, у=к/х, у=ax2+bx=c и описание их свойств; овладение умением использования алгоритма построения графика функции у = f(x+l), у = f(x) + т, у = f(x+l) + т; овладение навыками решения квадратных уравнений графическим способом, построения дробно-линейной функции. |
|
|
| 55 | § 17. Функция y= kx2, ее свойства и график. | 1 | Кусочно-заданные функции, контрольные точки графика, парабола, вершина параболы, ось симметрии параболы, фокус параболы, функция y= kx2 , график функции y= kx2. | Иметь представление о функции вида y= kx2, о её свойствах. (ПУ) Уметь решать графически уравнения и системы уравнений, определять число решений системы уравнений с помощью графического метода. | Иллюстрации на доске, сборник задач. |
|
|
| 56 | § 17. Функция y=kx2, ее свойства и график. | 1 |
| Знать свойства функции и писание по графику построенной функции. Уметь строить график функции y= kx2. (ПУ) Уметь упрощать функциональные выражения, строить графики кусочно-заданных функций, строить графики кусочно-заданных функций. | Раздаточный материал, диск сопровождения учебника. |
|
|
| 57 | § 17. Функция y=kx2, ее свойства и график. | 1 |
| Знать свойства функции и писание по графику построенной функции. Уметь строить график функции y= kx2. (ПУ) Уметь упрощать функциональные выражения, строить графики кусочно-заданных функций, строить графики кусочно-заданных функций. | Учебник, слайды, сборник задач. |
|
|
| 58 | § 17. Функция y=kx2, ее свойства и график. | 1 |
| Знать свойства функции и писание по графику построенной функции. Уметь строить график функции y= kx2. (ПУ) Уметь упрощать функциональные выражения, строить графики кусочно-заданных функций, строить графики кусочно-заданных функций. | Учебник, диск сопровождения учебника, раздаточный материал. |
|
|
| 59 | § 18. Функция y=k/x, ее свойства и график. | 1 | Функция у=1/x. Гипербола, ветви гиперболы, асимптоты, ось симметрии гиперболы. Функция у=к/х, обратная пропорциональность, коэффициент обратной пропорциональности, свойства функции у=к/х, область значений функции, окрестность точки, точка максимума, точка минимума. | Иметь представления о функции вида у=к/х, о её графике и свойствах. (ПУ) Уметь решать графически уравнения и системы уравнений, уметь определять число решений системы уравнений с помощью графического метода. | Учебник, демонстрация на доске. |
|
|
| 60 | § 18. Функция y=k/x, ее свойства и график. | 1 | Знать свойства функции и их описание по графику построенной функции. Уметь строить график функции у=к/х. (ПУ) Уметь упрощать функциональные выражения, строить график кусочно-заданных функций. | Учебник, раздаточный материал, слайды |
|
|
| 61 | § 18. Функция y=k/x, ее свойства и график. | 1 |
| Знать свойства функции и их описание по графику построенной функции. Уметь строить график функции у=к/х. (ПУ) Уметь упрощать функциональные выражения, строить график кусочно-заданных функций. | Учебник, слайды, раздаточный материал. |
|
|
| 62 | § 18. Функция y=k/x, ее свойства и график. | 1 |
| Знать свойства функции и их описание по графику построенной функции. Уметь строить график функции у=к/х. (ПУ) Уметь упрощать функциональные выражения, строить график кусочно-заданных функций. | Учебник, раздаточный материал. |
|
|
| 63 | Контрольная работа №4 по теме «Квадратичная функция. Функция у=к/х». | 1 |
| Уметь обобщать и систематизировать знания и умения по данной теме. | Контрольно-измерительный дифференцированный материал. |
|
|
| 64 | § 19. Как построить график функции у = f(x+l), если известен график функции у=f(x). | 1 | Параллельный перенос, параллельные перенос вправо (влево), вспомогательная система координат, алгоритм построения графика функции y=f(x+l). | Иметь представление как с помощью параллельного переноса вправо и влево построить график функции y=f(x+l). (ПУ) Уметь по алгоритму построить график функции у = f(x+l). | Учебник, слайды, раздаточный материал. |
|
|
| 65 | § 19. Как построить график функции у = f(x+l), если известен график функции у=f(x). | 1 |
| Иметь представление как с помощью параллельного переноса вправо и влево построить график функции y=f(x+l). (ПУ) Уметь по алгоритму построить график функции у = f(x+l). | Учебник, раздаточный материал. |
|
|
| 66 | § 19. Как построить график функции у = f(x+l), если известен график функции у=f(x). | 1 |
| Иметь представление как с помощью параллельного переноса вправо и влево построить график функции y=f(x+l). (ПУ) Уметь по алгоритму построить график функции у = f(x+l). | Учебник, слайды, учебника, раздаточный материал. |
|
|
| 67 | § 20. Как построить график функции у = f(x) + т, если известен график функции у=f(x). | 1 | Параллельный перенос, параллельный перенос вверх (вниз), вспомогательная система координат, алгоритм построения графика функции у = f(x) + т. | Иметь представление, как с помощью параллельного переноса вверх или вниз построить график функции у = f(x) + т. (ПУ) Уметь по алгоритму построить график функции у = f(x) + т, прочитать его и описать его свойства. | Учебник, демонстрация на доске. |
|
|
| 68 | § 20. Как построить график функции у = f(x) + т, если известен график функции у=f(x). | 1 |
| Иметь представление, как с помощью параллельного переноса вверх или вниз построить график функции у = f(x) + т. (ПУ) Уметь по алгоритму построить график функции у = f(x) + т, прочитать его и описать его свойства. | Учебник, слайды, раздаточный материал. |
|
|
| 69 | § 21. Как построить график функции у = f(x + l) + т, если известен график функции у=f(x). | 1 | Параллельный перенос, вспомогательная система координат, алгоритм построения графика функции у = f(x + l) + т. | Иметь представление, как с помощью параллельного переноса построить график функции у = f(x + l) + т. (ПУ) Уметь по алгоритму построить график функции у = f(x + l) + т, прочитать его и описать свойства. | Демонстрация на доске, учебник. |
|
|
| 70 | § 21. Как построить график функции у = f(x + l) + т, если известен график функции у=f(x). | 1 |
| Уметь строить график функции вида у = f(x + l) + т, описывать свойства функции по её графику. (ПУ) Уметь графически решать систему уравнений, строить график функции вида у = f(x + l) + т. | Учебник, раздаточный материал. |
|
|
| 71 | § 21. Как построить график функции у = f(x + l) + т, если известен график функции у=f(x). | 1 |
| Уметь строить график функции вида у = f(x + l) + т, описывать свойства функции по её графику. (ПУ) Уметь графически решать систему уравнений, строить график функции вида у = f(x + l) + т. | Учебник, раздаточный материал. |
|
|
| 72 | § 22. Функция у=ах2+bх+с, ее свойства и график. | 1 | Функция у=ах2+bх+с, квадратичная функция, график квадратичной функции, ось параболы, формула абсциссы параболы, алгоритм построения параболы у=ах2+bх+с | Иметь представление о функции у=ах2+bх+с, о её графике и свойствах. (ПУ) Уметь определять число корней уравнений и системы уравнений графическим методом. | Демонстрация на доске, учебник. |
|
|
| 73 | § 22. Функция у=ах2+bх+с, ее свойства и график. | 1 |
| Уметь строить график функции у=ах2+bх+с, описывать её свойства по графику. (ПУ) Уметь упрощать функциональные выражения, находить значения коэффициентов в формуле функции у=ах2+bх+с без построения графика функции. | Учебник, раздаточный материал. |
|
|
| 74 | § 22. Функция у=ах2+bх+с, ее свойства и график. | 1 |
| Уметь строить график функции у=ах2+bх+с, описывать её свойства по графику. (ПУ) Уметь упрощать функциональные выражения, находить значения коэффициентов в формуле функции у=ах2+bх+с без построения графика функции. | Учебник, демонстрация на доске |
|
|
| 75 | § 22. Функция у=ах2+bх+с, ее свойства и график. | 1 |
| Уметь строить график функции у=ах2+bх+с, описывать её свойства по графику. (ПУ) Уметь упрощать функциональные выражения, находить значения коэффициентов в формуле функции у=ах2+bх+с без построения графика функции. | Демонстрация на доске, раздаточный материал. |
|
|
| 76 | § 23. Графическое решение квадратных уравнений. | 1 | Квадратное уравнение, несколько способов графического решения уравнения. | Знать способы решения квадратных уравнений, применять их на практике. (ПУ) Уметь применять несколько способов решения уравнений. | Учебник, слайды, раздаточный материал. |
|
|
| 77 | § 23. Графическое решение квадратных уравнений. | 1 |
| Знать способы решения квадратных уравнений, применять их на практике. (ПУ) Уметь применять несколько способов решения уравнений. | Учебник, раздаточный материал. |
|
|
| 78 | Контрольная работа №5 по теме «Построение графика функции y=f(x+l)+m. Графическое решение квадратных уравнений». |
|
| Уметь обобщать и систематизировать знания по данной теме. | Контрольно-измерительный дифференцированный материал. |
|
|
|
| Г л а в а 4. Квадратные уравнения. | 24 | Цели: формирование представлений о полном, приведенном, неполном квадратном уравнении, дискриминанте квадратного уравнения, формулах корней квадратного уравнения, теореме Виета; формирование умений решить приведенное квадратное уравнение, применяя обратную теорему Виета; овладение умением разложения квадратного трехчлена на множители, решения квадратного уравнения по формуле корней квадратного уравнения; овладение навыками решения рационального и иррационального уравнения как математической модели реальных ситуаций.
|
|
|
| 79 | § 24. Квадратные уравнения. Основные понятия. | 1 | Квадратное уравнение, старший коэффициент, второй коэффициент, свободный член, приведенное квадратное уравнение, неполное квадратное уравнение, корень квадратного уравнения, решение квадратного уравнения. | Иметь представление о полном и неполном квадратном уравнении, о решении неполного квадратного уравнения. (ПУ) Уметь решать любые квадратные уравнения: приведенные полные, не приведенные полные, неполные. | Учебник, демонстрация на доске. |
|
|
| 80 | § 24. Квадратные уравнения. Основные понятия. | 1 |
| Уметь решать неполные квадратные уравнения и полные квадратные уравнения, разложив его левую часть на множители. (ПУ) Уметь решать рациональные уравнения и задачи на составление рациональных уравнений. | Раздаточный дифференцированный материал. |
|
|
| 81 | § 25. Формулы корней квадратных уравнений. | 1 | Дискриминант квадратного уравнения, формулы корней квадратного уравнения, правило решения квадратного уравнения. | Иметь представление о дискриминанте квадратного уравнения, формулах корней квадратного уравнения, об алгоритме решения квадратного уравнения. (ПУ) Уметь вывести формулу корней квадратного уравнения, если второй коэффициент нечетный. | Учебник, демонстрация на доске, раздаточный материал. |
|
|
| 82 | § 25. Формулы корней квадратных уравнений. | 1 |
| Знать алгоритм вычисления корней квадратного уравнения, используя дискриминант. Уметь решать квадратные уравнения по алгоритму. (ПУ) Уметь решать простейшие квадратные уравнения с параметрами и проводить исследование всех корней квадратного уравнения с параметрами. | Учебник, демонстрация на доске, раздаточный материал. |
|
|
| 83 | § 25. Формулы корней квадратных уравнений. | 1 |
| Уметь решать квадратные уравнения по формулам корней квадратного уравнения через дискриминант. (ПУ) Уметь решать задачи на составление квадратных уравнений. | Учебник, демонстрация на доске, раздаточный материал. |
|
|
| 84 | § 26. Рациональные уравнения. | 1 | Рациональные уравнения, алгоритм решения рационального уравнения, проверка корней квадратного уравнения, посторонние корни. | Иметь представление о рациональных уравнениях и об их решении. Знать алгоритм решения рациональных уравнений. (ПУ) Решение рациональных уравнений, используя метод введения новой переменной. | Учебник, демонстрация на доске. |
|
|
| 85 | § 26. Рациональные уравнения. | 1 |
| Уметь решать рациональные уравнения по заданному алгоритму и методом введения новой переменной. (ПУ) Решение биквадратных уравнений, уравнений с применением нескольких способов упрощения выражений, входящих в уравнение. | Учебник, слайды, раздаточный материал. |
|
|
| 86 | § 26. Рациональные уравнения. | 1 |
| Уметь решать рациональные уравнения по заданному алгоритму и методом введения новой переменной. (ПУ) Решение биквадратных уравнений, уравнений с применением нескольких способов упрощения выражений, входящих в уравнение. | Учебник, слайды, раздаточный материал. |
|
|
| 87 | § 26. Рациональные уравнения. | 1 |
| Уметь решать рациональные уравнения по заданному алгоритму и методом введения новой переменной. (ПУ) Решение биквадратных уравнений, уравнений с применением нескольких способов упрощения выражений, входящих в уравнение. | Учебник, слайды, раздаточный материал. |
|
|
| 88 | Контрольная работа №6 по теме «Квадратные уравнения». | 1 |
| Уметь обобщать и систематизировать знания и умения по данной теме. | Контрольно-измерительный дифференцированный материал. |
|
|
| 89 | § 27. Рациональные уравнения как математические модели реальных ситуаций. | 1 | Рациональные уравнения, математическая модель реальной ситуации, решение задач на составление уравнений. | Уметь решать задачи на числа, выделяя основные этапы математического моделирования. (ПУ) Свободное решение задач на числа, выделяя основные этапы математического моделирования. | Учебник, демонстрация на доске. |
|
|
| 90 | § 27. Рациональные уравнения как математические модели реальных ситуаций. | 1 |
| Уметь решать задачи на движение по воде, выделяя основные этапы математического моделирования. | Учебник, слайды, раздаточный материал. |
|
|
| 91 | § 27. Рациональные уравнения как математические модели реальных ситуаций. | 1 |
| Уметь решать задачи на движение по воде, выделяя основные этапы математического моделирования. | Учебник, дифференцированный раздаточный материал. |
|
|
| 92 | § 27. Рациональные уравнения как математические модели реальных ситуаций. | 1 |
| Уметь решать задачи на движение по воде, выделяя основные этапы математического моделирования. | Учебник, дифференцированный раздаточный материал. |
|
|
| 93 | § 28. Еще одна формула корней квадратного уравнения. | 1 | Квадратное уравнение с четным вторым коэффициентом, формулы корней квадратного уравнения с четным вторым коэффициентом. | Знать алгоритм вычисления корней квадратного уравнения с четным вторым коэффициентом, используя дискриминант. Свободное решение задач на движение по воде, выделяя основные этапы математического моделирования. (ПУ) Умение решать простейшие квадратные уравнения с четным вторым коэффициентом с параметрами и проводить исследование всех корней квадратного уравнения с четным вторым коэффициентом с параметром. | Учебник, дифференцированный раздаточный материал. |
|
|
| 94 | § 28. Еще одна формула корней квадратного уравнения. | 1 |
| Знать алгоритм вычисления корней квадратного уравнения с четным вторым коэффициентом, используя дискриминант. Свободное решение задач на движение по воде, выделяя основные этапы математического моделирования. (ПУ) Умение решать простейшие квадратные уравнения с четным вторым коэффициентом с параметрами и проводить исследование всех корней квадратного уравнения с четным вторым коэффициентом с параметром. | Учебник, слайды, раздаточный материал. |
|
|
| 95 | § 29. Теорема Виета. | 1 | Теорема Виета, обратная теорема Виета, симметрическое выражение с двумя переменными. | Иметь представление о теореме Виета и об обратной теореме Виета, о симметрических выражений с двумя переменными. (ПУ) Уметь составлять уравнения по его корням. Раскладывать на множители квадратный трехчлен. | Учебник, раздаточный материал. |
|
|
| 96 | § 29. Теорема Виета. | 1 |
| Уметь применять теорему Виета и обратную теорему Виета, решая квадратные уравнения. (ПУ) Уметь вычислять выражение, содержащее корни квадратного уравнения в виде неизвестных, применяя обратную теорему Виета. | Учебник, дифференцированный раздаточный материал. |
|
|
| 97 | § 29. Теорема Виета. | 1 |
| Уметь применять теорему Виета и обратную теорему Виета, решая квадратные уравнения. (ПУ) Уметь вычислять выражение, содержащее корни квадратного уравнения в виде неизвестных, применяя обратную теорему Виета. | Учебник, дифференцированный раздаточный материал. |
|
|
| 98 | Контрольная работа №7 по теме «Квадратное уравнение с четным вторым коэффициентом. Теорема Виета». | 1 |
| Уметь обобщать и систематизировать знания и умения по данной теме. | Контрольно-измерительный дифференцированный материал. |
|
|
| 99 | § 30. Иррациональные уравнения. | 1 | Иррациональные уравнения, метод возведения в квадрат, проверка корней, равносильные уравнения, равносильные преобразования уравнений, неравносильные преобразования уравнений. | Иметь представление об иррациональных уравнениях, о равносильных уравнениях, о равносильных и неравносильных преобразованиях уравнений. (ПУ) Уметь решать иррациональные уравнения, совершая равносильные переходы в преобразованиях. | Учебник, демонстрация на доске. |
|
|
| 100 | § 30. Иррациональные уравнения. | 1 |
| Уметь решать иррациональные уравнения методом возведения в квадрат обеих частей уравнения, применяя свойства равносильных преобразований. (ПУ) Уметь решать иррациональные уравнения, совершая равносильные переходы в преобразованиях; проверять корни, получившиеся при неравносильных преобразованиях. | Учебник, демонстрация на доске, раздаточный материал. |
|
|
| 101 | § 30. Иррациональные уравнения. | 1 |
| Уметь решать иррациональные уравнения методом возведения в квадрат обеих частей уравнения, применяя свойства равносильных преобразований. (ПУ) Уметь решать иррациональные уравнения, совершая равносильные переходы в преобразованиях; проверять корни, получившиеся при неравносильных преобразованиях. | Учебник, демонстрация на доске, раздаточный материал. |
|
|
| 102 | § 30. Иррациональные уравнения. | 1 |
| Уметь решать иррациональные уравнения методом возведения в квадрат обеих частей уравнения, применяя свойства равносильных преобразований. (ПУ) Уметь решать иррациональные уравнения, совершая равносильные переходы в преобразованиях; проверять корни, получившиеся при неравносильных преобразованиях. | Учебник, демонстрация на доске. |
|
|
|
| Глава 5. Неравенства. | 18 | Цель: формирование представлений о числовых неравенствах, о неравенстве с одной переменной, о модуле действительного числа; формирование умений исследования функции на монотонность, применяя способ приближенных вычислений; овладение умением построения графика функции модуль, описания её свойств; овладение навыками решения линейный, квадратных неравенства, решения неравенств, содержащих переменную величину под знаком модуль. |
|
|
| 103 | § 31. Свойства числовых неравенств. | 1 | Числовое неравенство, свойства числовых неравенств, неравенства одинакового смысла, неравенства противоположного смысла, среднее арифметические, среднее геометрическое, неравенство Коши. | Знать свойства числовых неравенств. Иметь представление о неравенстве одинакового смысла, противоположного смысла. (ПУ) Иметь представление о среднем арифметическом, о среднем геометрическом, о неравенстве Коши. Уметь выполнять действия с числовыми неравенствами, доказывать справедливость неравенств при любых значениях переменной. | Учебник, демонстрация на доске. |
|
|
| 104 | § 31. Свойства числовых неравенств. | 1 |
| Уметь применять свойства числовых неравенств и неравенство Коши при доказательстве числовых неравенств. (ПУ) Уметь доказывать справедливость числового неравенства методом выделения квадрата двучлена и используя неравенство Коши. | Учебник, раздаточный материал. |
|
|
| 105 | § 31. Свойства числовых неравенств. | 1 |
| Уметь применять свойства числовых неравенств и неравенство Коши при доказательстве числовых неравенств. (ПУ) Уметь доказывать справедливость числового неравенства методом выделения квадрата двучлена и используя неравенство Коши. | Учебник, раздаточный материал. |
|
|
| 106 | § 31. Свойства числовых неравенств. | 1 |
| Уметь применять свойства числовых неравенств и неравенство Коши при доказательстве числовых неравенств. (ПУ) Уметь доказывать справедливость числового неравенства методом выделения квадрата двучлена и используя неравенство Коши. | Учебник, раздаточный материал. |
|
|
| 107 | § 32. Исследование функций на монотонность. | 1 | Возрастающая функция на промежутке, убывающая функция на промежутке, функция у=х2, функция у=1/х, функция у=√x, линейная функция. Монотонная функция. | Иметь представление о возрастающей, убывающей, монотонной функции на промежутке. (ПУ) Уметь исследовать различные функции на монотонность; решать уравнения, используя свойства монотонности. | Учебник, раздаточный материал. |
|
|
| 108 | § 32. Исследование функций на монотонность. | 1 |
| Уметь построить и исследовать на монотонность функции: линейную, квадратную, обратной пропорциональности, функцию корень. (ПУ) Уметь исследовать на монотонность кусочно-заданные функции; решать уравнения и неравенства, используя свойства монотонности. | Учебник, раздаточный материал. |
|
|
| 109 | § 32. Исследование функций на монотонность. | 1 |
| Уметь построить и исследовать на монотонность функции: линейную, квадратную, обратной пропорциональности, функцию корень. (ПУ) Уметь исследовать на монотонность кусочно-заданные функции; решать уравнения и неравенства, используя свойства монотонности. | Учебник, раздаточный материал. |
|
|
| 110 | § 33. Решение линейных неравенств. | 1 | Неравенство с переменной, решение неравенства с переменной, множество решений, система линейных неравенств, пересечение решений неравенств системы. | Иметь представление о неравенстве с переменной, о системе линейных неравенств, о пересечении решений неравенств системы. (ПУ) Уметь изобразить на координатной плоскости точки, координаты которых удовлетворяют неравенству. | Учебник, раздаточный материал. |
|
|
| 111 | § 33. Решение линейных неравенств. | 1 |
| Уметь решать неравенства с одной переменной и системы линейных неравенств. (ПУ) Уметь решать задачу, выделяя три этапа математического моделирования. | Учебник, демонстрация на доске, раздаточный материал. |
|
|
| 112 | § 33. Решение линейных неравенств. | 1 |
| Уметь решать неравенства с одной переменной и системы линейных неравенств. (ПУ) Уметь решать задачу, выделяя три этапа математического моделирования. | Контрольно-измерительный дифференцированный материал. |
|
|
| 113 | § 34. Решение квадратных неравенств. | 1 | Квадратное неравенство, знак объединения множеств. Алгоритм решения квадратного неравенства, метод интервалов. | Иметь представление о квадратном неравенстве, о знаке объединения множеств, об алгоритме решения квадратного неравенства, о методе интервалов. (ПУ) Уметь решать квадратное неравенство методом интервалов. | Учебник, демонстрация на доске, раздаточный материал. |
|
|
| 114 | § 34. Решение квадратных неравенств. | 1 |
| Знать, как решать квадратное неравенство по алгоритму и методом интервалов. |
|
|
|
| 115 | § 34. Решение квадратных неравенств. | 1 |
| Знать, как решать квадратное неравенство по алгоритму и методом интервалов. (ПУ) Уметь решать квадратные неравенства, применяя равносильные преобразования выражений; решать квадратичные неравенства с параметрами. | Учебник, раздаточный материал. |
|
|
| 116 | § 34. Решение квадратных неравенств. | 1 |
| Знать, как решать квадратное неравенство по алгоритму и методом интервалов. (ПУ) Уметь решать квадратные неравенства, применяя равносильные преобразования выражений; решать квадратичные неравенства с параметрами. | Учебник, раздаточный материал. |
|
|
| 117 | Контрольная работа №8 по теме «Числовые и квадратные неравенства». | 1 |
| Уметь обобщать и систематизировать знания и умения по данной теме. | Контрольно-измерительный дифференцированный материал. |
|
|
| 118 | § 35. Приближенные значения действительных чисел. | 1 | Приближенное значение по недостатку, приближенное значение по избытку, округление чисел, погрешность приближения, абсолютная погрешность, относительная погрешность. | Знать о приближенном значении по недостатку или по избытку, об округлении числа, о погрешности приближения, об абсолютной и относительной погрешности. (ПУ) Уметь использовать знания о приближении по недостатку или по избытку, об округлении чисел, абсолютной и относительной погрешности. | Учебник, демонстрация на доске, раздаточный материал. |
|
|
| 119 | § 35. Приближенные значения действительных чисел. | 1 |
| Знать о приближенном значении по недостатку или по избытку, об округлении числа, о погрешности приближения, об абсолютной и относительной погрешности. (ПУ) Уметь использовать знания о приближении по недостатку или по избытку, об округлении чисел, абсолютной и относительной погрешности. | Учебник, демонстрация на доске, раздаточный материал. |
|
|
| 120 | § 36. Стандартный вид положительного числа. | 1 |
| Знать о приближенном значении по недостатку или по избытку, об округлении числа, о погрешности приближения, об абсолютной и относительной погрешности. (ПУ) Уметь использовать знания о приближении по недостатку или по избытку, об округлении чисел, абсолютной и относительной погрешности. | Учебник, демонстрация на доске, раздаточный материал. |
|
|
|
| Случайные события и их вероятности | 3 | Цель: формирование представлений о сборе и группировке статистических данных; формирование умений представления статистической информации; овладение умением построения графика статистической информации; |
|
|
| 121 | Сбор и группировка статистических данных |
|
| Знать о способах сбора и группировки статистических данных, о способах их обработки. |
|
|
|
| 122 | Наглядное представление статистической информации |
|
| Уметь представлять собранные данные в таблицах, уметь их анализировать. |
|
|
|
| 123 | Наглядное представление статистической информации |
|
| Уметь строить графики, диаграммы о собранным таблицам, представлять статистическую информацию в графической форме |
|
|
|
|
| Обобщающее повторение. | 13 | Цель: обобщить и систематизировать знания тем курса алгебры 8 класса с решением заданий повышенной сложности; формирование понимания возможности использования приобретенных знаний и умений в практической деятельности. |
|
|
| 124 | Итоговое повторение. Алгебраические дроби. | 1 | Преобразование рациональных выражений, решений рациональных уравнений. | Уметь применять основное свойство дроби при преобразовании алгебраических дробей и их сокращении. (ПУ) Уметь преобразовывать тройки алгебраических дробей с одинаковым знаменателем, раскладывать числитель и знаменатель дроби на простые множители. | Учебник, демонстрация на доске, раздаточный материал. |
|
|
| 125 | Итоговое повторение. Алгебраические дроби. | 1 |
| Уметь преобразовывать рациональные выражения, используя все действия с алгебраическими дробями. (ПУ) Уметь доказывать тождества, решать рациональные уравнения, задачи, выделяя три этапа математического моделирования. | Учебник, демонстрация на доске, раздаточный материал. |
|
|
| 126 | Итоговое повторение. Алгебраические дроби. | 1 |
| Уметь преобразовывать рациональные выражения, используя все действия с алгебраическими дробями. (ПУ) Уметь доказывать тождества, решать рациональные уравнения, задачи, выделяя три этапа математического моделирования. | Учебник, демонстрация на доске, раздаточный материал. |
|
|
| 127 | Итоговое повторение. Функция y= √x. Свойства квадратного корня. | 1 | Функция у=√x, ее свойства и график, функция, выпуклая вверх, функция, выпуклая вниз. | Уметь строить график функции у=√x, знать ее свойства. (ПУ) Умет читать график функции, решать графически уравнения и системы уравнений. | Учебник, демонстрация на доске, раздаточный материал. |
|
|
| 128 | Итоговое повторение. Функция y= √x. Свойства квадратного корня. | 1 |
| Уметь строить график функции у=√x, знать ее свойства. (ПУ) Умет читать график функции, решать графически уравнения и системы уравнений. | Учебник, демонстрация на доске, раздаточный материал. |
|
|
| 129 | Итоговое повторение. Функция y= √x. Свойства квадратного корня. | 1 |
| Уметь строить график функции у=√x, знать ее свойства. (ПУ) Умет читать график функции, решать графически уравнения и системы уравнений. | Учебник, демонстрация на доске, раздаточный материал. |
|
|
| 130 | Итоговое повторение. Квадратичная функция. Функция y= k/x. | 1 | Функция у=1/x. Гипербола, ветви гиперболы, асимптоты, ось симметрии гиперболы. Функция у=к/х, обратная пропорциональность, коэффициент обратной пропорциональности, свойства функции у=к/х, область значений функции, окрестность точки, точка максимума, точка минимума. | Знать свойства функции и их описание по графику построенной функции. Уметь строить график функции у=к/х. (ПУ) Уметь упрощать функциональные выражения, строить график кусочно-заданных функций. | Учебник, демонстрация на доске, раздаточный материал. |
|
|
| 131 | Итоговое повторение. Квадратичная функция. Функция y= k/x. | 1 |
| Знать свойства функции и их описание по графику построенной функции. Уметь строить график функции у=к/х. (ПУ) Уметь упрощать функциональные выражения, строить график кусочно-заданных функций. | Учебник, демонстрация на доске, раздаточный материал. |
|
|
| 132 | Итоговое повторение. Квадратные уравнения. | 1 | Формулы корней квадратного уравнения, теорема Виета и обратная её, разложение квадратного трехчлена на множители. | Уметь решать квадратные уравнения по формулам корней квадратного уравнения через дискриминант. (ПУ) Уметь решать задачи на составление квадратных уравнений. | Учебник, демонстрация на доске, раздаточный материал. |
|
|
| 133 | Итоговое повторение. Квадратные уравнения. | 1 |
| Уметь применять теорему Виета и обратную ей, решая квадратные уравнения. (ПУ) Уметь, не решая квадратное уравнение, вычислять выражение, содержащее корни этого уравнения в виде неизвестных, применяя обратную теорему Виета. | Учебник, демонстрация на доске, раздаточный материал. |
|
|
| 134 | Итоговое повторение. Неравенства. | 1 | Решение линейных и квадратных неравенств, исследование функции на монотонность. | Уметь решать линейные и квадратные неравенства с одной переменной; решать линейные и квадратные неравенства с одной переменной, содержащие модуль; решать неравенства графически. (ПУ) Решать простые линейные и квадратные неравенства с параметром. | Учебник, демонстрация на доске, раздаточный материал. |
|
|
| 135 | Итоговое повторение. Неравенства. | 1 |
| Уметь решать линейные и квадратные неравенства с одной переменной; решать линейные и квадратные неравенства с одной переменной, содержащие модуль; решать неравенства графически. (ПУ) Решать простые линейные и квадратные неравенства с параметром. | Учебник, демонстрация на доске, раздаточный материал. |
|
|
| 136 | Обобщающий урок. | 1 |
| Уметь обобщать и систематизировать знания по основным темам курса. | Учебник, демонстрация на доске, раздаточный материал. |
|
|

 Получите свидетельство
Получите свидетельство Вход
Вход











 Рабочая программа по математике (алгебра, 8 класс) (0.46 MB)
Рабочая программа по математике (алгебра, 8 класс) (0.46 MB)
 0
0 1202
1202 137
137 Нравится
0
Нравится
0





