Рабочая программа по математике для 7 класса по учебникам для общеобразовательных учреждений: «Алгебра 7» А.Г.Мордкович, «Геометрия 7 – 9» Л.С.Атанасян, В.Ф.Бутузов, С.Б. Кадомцев и др.
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Статус документа
Рабочая программа по предмету математика составлена на основе примерной программы по математике/ Письмо МОН РФ от 07.07 2005г. № 03-1263 «О примерных программах по учебным предметам федерального базисного учебного плана» и в соответствии с федеральным компонентом государственного стандарта начального общего, основного общего и среднего (полного) общего образования /Приказ МО РФ от 5 марта 2004 г. № 1089 «Об утверждении федерального компонента государственных образовательных стандартов начального общего, основного общего и среднего (полного) общего образования». Рабочая программа конкретизирует содержание предметных тем образовательного стандарта и дает распределение учебных часов по разделам курса. Согласно базисному учебному плану средней (полной) школы, рекомендациям Министерства образования Российской Федерации и наличию учебников в библиотеке, выбрана данная учебная программа и учебно-методический комплект.
Общая характеристика предмета математика
Курс математики 7 класса включает следующие разделы: арифметика, алгебра, геометрия которые изучаются блоками.
Арифметика призвана способствовать приобретению практических навыков, необходимых для повседневной жизни. Она служит базой для всего дальнейшего изучения математики, способствует логическому развитию и формированию умения пользоваться алгоритмами.
Алгебра. Изучение алгебры нацелено на формирование математического аппарата для решения задач из математики, смежных предметов, окружающей реальности. Язык алгебры подчеркивает значение математики как языка для построения математических моделей, процессов и явлений реального мира (одной из основных задач изучения алгебры является развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики; овладение навыками дедуктивных рассуждений). Преобразование символических форм вносит свой специфический вклад в развитие воображения, способностей к математическому творчеству. Другой важной задачей изучения алгебры является получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов (равномерных, равноускоренных, экспоненциальных, периодических и др.), для формирования у обучающихся представлений о роли математики в развитии цивилизации и культуры.
Геометрия — один из важнейших компонентов математического образования, необходимый для приобретения конкретных знаний о пространстве и практически значимых умений, формирования языка описания объектов окружающего мира, для развития пространственного воображения и интуиции, математической культуры, для эстетического воспитания обучающихся. Изучение геометрии вносит вклад в развитие логического мышления, в формирование понятия доказательства.
Таким образом, в ходе освоения содержания курса учащиеся получают возможность:
инструментальных вычислений, развивать вычислительную культуру;
овладеть символическим языком алгебры, выработать формально-оперативные алгебраические умения и научиться применять их к решению математических и нематематических задач;
изучить свойства и графики элементарных функций, научиться использовать функционально-графические представления для описания и анализа реальных зависимостей;
развить пространственные представления и изобразительные умения, освоить основные факты и методы планиметрии, познакомиться с простейшими пространственными телами и их свойствами;
получить представления о статистических закономерностях в реальном мире и о различных способах их изучения, об особенностях выводов и прогнозов, носящих вероятностный характер;
развивать логическое мышление и речь - умения логически обосновывать суждения, проводить несложные систематизации, приводить примеры и контрпримеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства;
сформировать представления об изучаемых понятиях и методах как важнейших средствах математического моделирования реальных процессов и явлений.
Изучение математики на ступени основного общего образования направлено на достижение целей:
овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
интеллектуальное развитие, формирование качеств, необходимых для полноценной жизни в современном обществе, свойственных математической деятельности; ясности и точности мысли, критичности мышления, интуиции, логического мышления, алгоритмической культуры, пространственных представлений, способности к преодолению трудностей.
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов
воспитание культуры личности, отношения к математике как части общечеловеческой культуры
Решаются следующие задачи:
систематизация сведений о числах;
изучение новых видов числовых выражений и формул;
совершенствование практических навыков и вычислительной культуры,
расширение и совершенствование арифметического аппарата, сформированного в начальной школе, и его применение к решению математических и нематематических задач.
развитие представлений о вероятностно-статистических закономерностях в окружающем мире, совершенствование интеллектуальных и речевых умений путем обогащения математического языка, развития логического мышления.
При изучении начального курса геометрии все новые понятия, теоремы, свойства геометрических фигур, способы рассуждений усваивать в процессе решения практических задач.
Место предмета математика в базисном учебном плане
В соответствии с федеральным базисным учебным планом и авторскими программами рабочая программа рассчитана на 6 ч в неделю. Всего 204 ч, из них 136 ч – на изучение алгебры и 68 ч - геометрии. Преподавание предмета «Математика» осуществляется в форме последовательных тематических блоков с чередованием материала по алгебре и геометрии. В классных журналах для фиксации прохождения программы используется одна страница (наименование предмета «Математика»). Разбивка часов курса по блокам и темам уроков по алгебре и геометрии осуществляется на основе авторской программы.
Реализация обучения математике осуществляется через личностно-ориентированную технологию, где учебная деятельность, в основном, строится следующим образом: введение в тему, изложение нового материала. Отработка теоретического материала, практикум по решению задач, итоговый контроль.
ОСНОВНОЕ СОДЕРЖАНИЕ
Повторение за курс 6 класса
Математический язык. Математическая модель. (16 часов)
Числовые и алгебраические выражения. Переменная. Допустимое значение переменной. Недопустимое значение переменной. Линейное уравнение с одной переменной. Линейные уравнения как математические модели реальных ситуаций.
Основная цель - сформировать понятие числового выражения и выражения с переменными, уметь выполнять тождественные преобразования. Выработать навыки решения линейных уравнений и задач с помощью линейных уравнений.
Начальные понятия и теоремы геометрии. (10 часов)
Возникновение геометрии. Прямая и отрезок. Луч и угол. Сравнение отрезков и углов. Измерение отрезков. Измерение углов. Смежные и вертикальные углы. Перпендикулярные прямые.
Основная цель - систематизировать знания учащихся о взаимном расположении точек и прямых; уметь изображать, обозначать отрезки, лучи, углы, а также сравнивать их и измерять; строить смежные, вертикальные углы и перпендикулярные прямые.
Линейная функция. (17 часов)
Координатная плоскость. Алгоритм отыскания координатной плоскости. Алгоритм построения точки М(а;b) в прямоугольной системе координат.
Линейное уравнение с двумя переменными. Решение уравнения ax+by+c=0. График уравнения. Алгоритм построения графика уравнения ax+by+c=0
Линейная функция .Независимая переменная (аргумент).Зависимая переменная. График линейной функции. Наибольшее и наименьшее значения линейной функции на заданном промежутке. Возрастание и убывание линейной функции.
Линейная функция y=kx и ее график.
Взаимное расположение графиков линейных функций.
Основная цель - иметь понятие о функциональной зависимости, области определения функции. Уметь задавать функцию, строить графики линейной функции и функцию, описывающую прямую пропорциональную зависимость.
Системы двух линейных уравнений с двумя переменными(15 часов)
Система уравнений. Решение системы уравнений. Графический метод решения системы уравнений. Метод подстановки. Метод алгебраического сложения.
Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций (текстовые задачи)
Треугольники. (18 часов)
Треугольник. Признаки равенства треугольников. Перпендикуляр к прямой. Высота, медиана, биссектриса треугольника. Равнобедренные и равносторонние треугольники; свойства и признаки равнобедренного треугольника. Основные задачи на построение с помощью циркуля и линейки.
Основная цель - знать признаки равенства треугольников, уметь из использовать при решении задач; иметь понятие о равнобедренном и равностороннем треугольниках, знать их признаки и свойства; уметь решать основные задачи на построение с помощью циркуля и линейки.
Степень с натуральным показателем. (9 часов)
Степень. Основание степени. Показатель степени. Свойства степени с натуральным показателем.
Умножение и деление степеней с одинаковыми показателями. Степень с нулевым показателем.
Основная цель - иметь понятие о степени числа a с натуральным показателем; уметь умножать, делить степени, а также возводить в степень произведение и степень
Одночлены. Операции над одночленами. (8 часов)
Одночлен. Коэффициент одночлена .Стандартный вид числа. Подобные одночлены. Сложение одночленов. Умножение одночленов. Возведение одночлена в натуральную степень. Деление одночлена на одночлен.
Основная цель- иметь понятие об одночлене. Уметь умножать одночлены, возводить их в степень; развивать вычислительные навыки учащихся.
Параллельные прямые. (13 часов)
Признаки параллельности прямых. Аксиома параллельных прямых. Свойства параллельных прямых.
Основная цель - понимать, какие отрезки и лучи называются параллельными; уметь применять аксиому параллельных прямых и следствия из нее при решении задач.
Многочлены. Арифметические операции над многочленами. (18 часов)
Многочлен и его стандартный вид. Сложение и вычитание многочленов. Умножение одночлена на многочлен. Умножение многочлена на многочлен.
Квадрат суммы и квадрат разности. Разность квадратов. Разность кубов и сумма кубов. Деление многочлена на многочлен.
Основная цель - иметь понятие о многочлене, уметь приводить подобные слагаемые; складывать, вычитать многочлены, а также умножать одночлен на многочлен и многочлен на многочлен при выполнении упражнений и решении уравнений; развивать вычислительные навыки.
Соотношения между сторонами и углами треугольника. (6 часов)
Сумма углов треугольника. Внешние углы треугольника. Прямоугольные, остроугольные и тупоугольные треугольники. Зависимость между величинами сторон и углов треугольника. Неравенство треугольника.
Разложение многочленов на множители (22 часа)
Вынесение общего множителя за скобки. Способ группировки. Разложение многочлена на множители. Разложение многочлена на множители с помощью формул сокращенного умножения, комбинация различных приемов. Метод выделения полного квадрата.
Понятие алгебраической дроби. Сокращение алгебраической дроби.
Тождество. Тождественно равные выражения. Тождественные преобразования.
Основная цель - иметь навыки применения формул сокращенного умножения для упрощения выражений, решения уравнений и задач. Уметь применять различные способы для разложения на множители.
Прямоугольные треугольники (12 часов)
Некоторые свойства прямоугольных треугольников. Признаки равенства прямоугольных треугольников. Расстояние от точки до прямой. Расстояние между параллельными прямыми. Построение треугольника по трем сторонам.
Основная цель - уметь решать задачи, используя теоремы о сумме углов треугольника, о соотношениях между сторонами и углами треугольника, о неравенстве треугольника и следствий из них; знать признаки равенства прямоугольных треугольников и уметь их использовать при решении задач; уметь строить треугольник по трем элементам.
Функция y=x2 (11 часов) .
Функция y=x2 ,ее свойства и график. Функция y=-x2 ,ее свойства и график.
Графическое решение уравнений.
Кусочная функция. Чтение графика функции. Область определения функции. Первое представление о непрерывных функциях Точка разрыва. Разъяснение смысла записи y=f(x). Функциональная символика.
Элементы статистической обработки данных (7 часов)
Итоговое повторение . (19 часов)
Основная цель - повторить и обобщить основные темы, изученные за учебный год.
Количество контрольных работ - 14
ТРЕБОВАНИЯ К УРОВНЮ ПОДГОТОВКИ СЕМИКЛАССНИКОВ.
В результате изучения математики ученик должен:
Знать/понимать
• Существо понятия алгоритма; примеры алгоритмов;
• Как используются математические формулы, уравнения; примеры их применения для решения алгебраических и геометрических практических задач;
• Как потребности практики привели математическую науку к необходимости расширения понятия числа.
Уметь
• выполнять тождественные преобразования выражений;
• решать линейные уравнения и задачи с помощью линейных уравнений;
• строить графики линейной функции и функции, описывающей прямую пропорциональную зависимость;
• выполнять действия со степенями и одночленами;
• находить сумму, разность, произведение многочленов; умножать одночлен на многочлен;
• применять формулы сокращенного умножения для различных способов разложения на множители;
• решать системы линейных уравнений и задач с помощью систем линейных уравнений;
• строить смежные и вертикальные углы и находить их градусные меры;
• решать задачи на применение признаков равенства треугольников;
• решать основные задачи на построение с помощью циркуля и линейки;
• использовать аксиому параллельных прямых для решения задач;
• доказывать теоремы о сумме углов треугольника, о соотношениях между сторонами и углами треугольника. О неравенстве треугольников и применять их к решению задач;
• применять признаки равенства прямоугольных треугольников к решению задач;
• строить треугольники по трем элементам;
• проводить несложные доказательства, получать следствия из известных или ранее полученных утверждений, оценивать логическую правильность рассуждений, использовать примеры для иллюстрации и контрпримеры для опровержения утверждений.
Учебный план.
| Разделы программы | Всего часов | Дом. контр. раб. | Сам. раб. | Контр. раб. |
| Повторение за курс 6 класса | 4 ч |
|
|
|
| Математический язык. Математическая модель. | 16 ч | 1 |
| 1 |
| Начальные геометрические сведения | 10 ч |
|
| 1 |
| Линейная функция. | 17 ч | 1 |
| 1 |
| Система двух линейных уравнений с двумя переменными. | 15 ч | 1 |
| 1 |
| Треугольники | 18 ч |
|
| 1 |
| Степень с натуральным показателем и её свойства. | 9 ч | 1 |
|
|
| Одночлены. Операции над одночленами. | 8 ч | 1 |
| 1 |
| Параллельные прямые | 13 ч |
|
| 1 |
| Многочлены и операции над многочленами. | 18 ч | 1 |
| 1 |
| Соотношение между сторонами и углами треугольника | 6 ч |
|
| 1 |
| Разложение многочленов на множители. | 22 ч | 1 |
| 1 |
| Прямоугольные треугольники | 12 ч |
|
| 1 |
| Функция 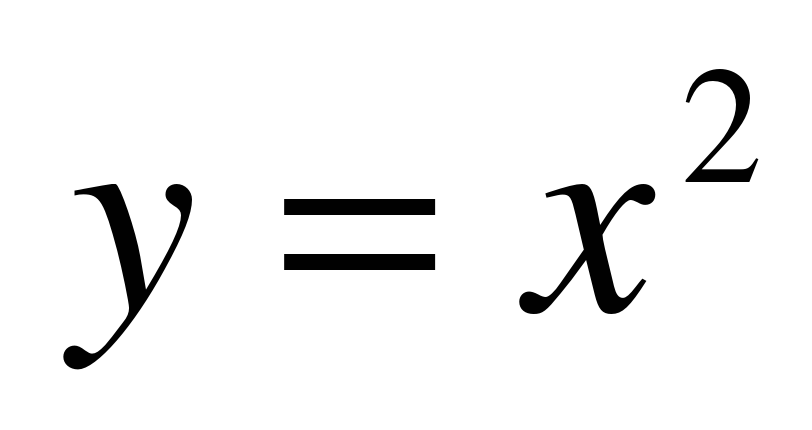 . . | 11 ч | 1 |
| 1 |
| Элементы статистической обработки данных | 8 ч |
|
|
|
| Итоговое повторение и итоговая контрольная работа. | 19 ч | 1 |
| 2 |
| Итого: | 204 ч | 9 |
|
|
Календарно-тематическое планирование
Календарно – тематическое планирование по математике в 7 классе (6 часов в неделю всего 204 часа)
| № ур | № дид.ед. | Тема урока | Цель по обеспечению достижения базового и повышенного уровня | Учебная деятельность в рамках урока
| Формы контроля | Домашнее здание | Дата проведения урока
|
| По плану | Фактически |
| Повторение (4 часа) |
| 1 | 1 | Обыкновенные дроби, десятичные дроби | Знать: - основные понятия темы: обыкновенная дробь, десятичная дробь, алгоритмов сравнения, сложения, вычитания, умножения, деления дробей; - приёмы рационального выполнения вычислений с дробями. Уметь: решать задачи с использованием 2-3 алгоритмов | Повторение алгоритмов сравнения, сложения, вычитания, умножения, деления обыкновенных и десятичных дробей. Совершенствование навыков решения задач с использованием 2-3 алгоритмов | Фронтальный опрос | Сборник за 6 класс, С-15.3 № 2 (вар. 1); С-21.2 № 2 (вар. 1); С-22.2 № 3 (вар. 1)
|
|
|
| 2 | 1 | Положительные и отрицательные числа | Знать: -основные понятия темы: положительное число, отрицательное число, модуль, противоположные числа; алгоритмы сравнения, сложения, вычитания, умножения, деления положительных и отрицательных чисел; - приёмы рационального выполнения вычислений с положительными и отрицательными числами. Уметь: решать задачи с использованием 2-3 алгоритмов | Повторение алгоритмов сравнения, сложения, вычитания, умножения, деления положительных и отрицательных чисел. Совершенствование навыков решения задач с использованием 2-3 алгоритмов | Фронтальный опрос Проверочная работа | Сборник за 6 класс, С-8.3. № 1, № 3 (вар. 1); С-14.2, № 3 (вар.1); С-15.4 № 1 (вар. 1)
|
|
|
| 3 | 1 | Преобразование выражений | Знать: -законы арифметических действий: переместительного, сочетательного, распределительного; способов преобразования алгебраических выражений; -приёмы рационального выполнения преобразования выражений. Уметь: -решать задачи с использованием 2-3 алгоритмов; -использовать приёмы рационального решения задач | Повторение законов арифметических действий, способов преобразования алгебраических выражений. Совершенствование навыков решения задач с использованием 2-3 алгоритмов
| Работа по группам | Сборник за 6 класс, С-17.2; С-18.2 (задания 1 вар.) |
|
|
| 4 | 1 | Решение уравнений | Знать: -основные понятия темы: уравнение, корень уравнения; алгоритма решения линейного уравнения: - приёмов рационального решения линейных уравнений. Уметь: -решать задачи с использованием 2-3 алгоритмов; -использовать приёмы рационального решения задач | Повторение свойств уравнений и тождественных преобразований при решении уравнений. Совершенствование навыков решения задач с использованием 2-3 алгоритмов
| Индиви дуальные карточки | Сборник за 6 класс, С-19.2(вар.1); С-19.3 № 1, № 2 (вар.1)
|
|
|
| Математический язык. Математическая модель. (16 часов) |
|
| 5 | 1 | Числовые и алгебраические выражения. | Б: Научить: -выполнять вычисления с рациональными числами, сочетая устные и письменные приемы вычислений; - решать задачи, содержащие буквенные данные, работать с формулами; - выполнять преобразования выражений; - решать линейные уравнения с одной переменной; - понимать уравнение как важнейшую математическую модель для описания и изучения разнообразных реальных ситуаций, решать текстовые задачи алгебраическим методом. П: дать возможность: научиться использовать приемы, рационализирующие вычисления, приобрести привычку контролировать вычисления, выбирая подходящий для ситуации способ; - применять тождественные преобразования для решения задач из различных разделов курса; - овладеть специальными приемами решения уравнений; уверенно применять аппарат уравнений для решения разнообразных задач из математики, смежных предметов, практики. | Определять числовые и буквенные выражения. Свойства действий. Допустимые и не допустимые значения переменных. Выполнять элементарные знаково-символические действия, применять буквы для обозначения чисел, для записи общих утверждений; | ФО
|
|
|
|
| 6 | 1 | Решение задач по теме: «Числовые и алгебраические выражения». | Находить значение числового выражения. Находить значение алгебраического выражения при заданных значениях переменных. Определять значения переменных, при которых имеет смысл выражение. | ИРД
|
|
|
|
| 7 | 1 | Решение задач по теме: «Числовые и алгебраические выражения».
| Рассмотрение приёмов: - нахождения значения числового выражения рациональным способом; - рационального упрощения алгебраических выражений |
|
|
|
|
| 8 | 1 | Решение задач по теме: «Числовые и алгебраические выражения».
| вычислять числовые значения буквенных выражений; - находить допустимые значения переменных; - выполнять элементарные знаково-символические действия: применять буквы для обозначения чисел, для записи общих утверждений
| С.р. |
|
|
|
| 9 | 1 | Что такое математический язык. | Запись утверждений на языке математики. Составлять буквенные выражения по условиям, заданным словесно, рисунком или чертежом; преобразовывать алгебраические суммы и произведения (выполнять приведение подобных слагаемых, раскрытие скобок, упрощение произведений). |
|
|
|
|
| 10 | 1 | Что такое математический язык. Самостоятельная работа. | осуществлять «перевод» выражений с математического языка на обычный язык и обратно, «переводить» математические правила, законы в символическую форму, осуществлять «обратный перевод». |
|
|
|
|
| 11 | 1 | Что такое математическая модель. | составлять математическую модель реальной ситуации, используя математический язык; решать текстовые задачи с помощью математического моделирования. |
|
|
|
|
| 12 | 1 | Решение задач по теме «Что такое математическая модель» | составлять математическую модель реальной ситуации, используя математический язык; решать текстовые задачи с помощью математического моделирования. |
|
|
|
|
| 13 | 1 | Решение задач по теме «Что такое математическая модель» | Использовать для познания окружающего мира различные методы (наблюдение, измерение, моделирование). |
|
|
|
|
| 14 | 1 | Линейное уравнение с одной переменной. | решать линейные уравнения; текстовые задачи с помощью математического моделирования. |
|
|
|
|
| 15 | 1 | Решение задач по теме: «Линейное уравнение с одной переменной». | решать линейные уравнения; текстовые задачи с помощью математического моделирования. |
|
|
|
|
| 16 | 1 | Решение задач по теме: «Линейное уравнение с одной переменной». | распознавать линейные уравнения, решать линейные уравнения, а также уравнения, сводящиеся к ним. Решать текстовые задачи алгебраическим способом. |
|
|
|
|
| 17 | 1 | Координатная прямая. | отмечать на координатной прямой точку с заданной координатой, определять координату точки, вид промежутка; связывать геометрическую и аналитическую модели промежутка, выбирать адекватное обозначение и символическую запись. |
|
|
|
|
| 18 | 1 | Решение задач по теме: «Координатная прямая». | отмечать на координатной прямой точку с заданной координатой, определять координату точки, вид промежутка; связывать геометрическую и аналитическую модели промежутка, выбирать адекватное обозначение и символическую запись. |
|
|
|
|
| 19 | 1 | Решение задач по теме: «Математический язык. Математическая модель» | Решать текстовые задачи алгебраическим способом: переходить от словесной формулировки условия задачи к алгебраической модели путем составления уравнения; решать составленное уравнение; интерпретировать результат.
|
|
|
|
|
| 20 | 1 | Контрольная работа по теме: «Математический язык. Математическая модель» | Уметь применять изученный теоретический материал при выполнении письменной работы
| самостоятельно выбирать рациональный способ решения задач. |
|
|
|
|
| Начальные геометрические сведения (10 часов) |
|
| 21 | 1 | Прямая и отрезок. | Б: Научить: - пользоваться языком геометрии для описания предметов окружающего мира и их конфигурации; - распознавать и изображать на чертежах и рисунках геометрические фигуры и их конфигурации; - использовать свойства измерения длин и углов при решении задач на нахождение длин отрезков и градусной меры угла; - находить градусную меру углов, применяя определения и свойства смежных и вертикальных углов. П: дать возможность: - приобрести опыт применения алгебраического аппарата при решении геометрических задач. | Обозначать отрезки, точки и прямые на рисунке, изображать их возможное взаимное расположение, |
|
|
|
|
| 22 | 1 | Луч и угол | Изображать и обозначать лучи на рисунке, обозначать развёрнутые и неразвёрнутые углы, называть по рисунку элементы угла. |
|
|
|
|
| 23 | 1 | Сравнение отрезков и углов. С.р. | Сравнивать отрезки и углы, отмечать с помощью линейки середину отрезка, с помощью транспортира проводить середину угла. |
|
|
|
|
| 24 | 1 | Измерение отрезков | Измерить данный отрезок и выразить его длину в см., мм., м.; находить длину отрезка, разделённого на 2 части точкой, длины которых известны. |
|
|
|
|
| 25 | 1 | Измерение отрезков. | Измерить данный отрезок и выразить его длину в см., мм., м.; находить длину отрезка, разделённого на 2 части точкой, длины которых известны. |
|
|
|
|
| 26 | 1 | Измерение углов. С.Р. | Измерять углы с помощью транспортира, изображать прямой, острый, тупой, развёрнутый углы; |
|
|
|
|
| 27 | 1 | Смежные и вертикальные углы | строить угол, смежный с данным, вертикальные углы. |
|
|
|
|
| 28 | 1 | Перпендикулярные прямые | Объяснять, почему две прямые, перпендикулярные третьей, не пересекаются, решать задачи о нахождении градусной меры смежных и вертикальных углов. |
|
|
|
|
| 29 | 1 | Решение задач |
|
|
|
|
|
| 30 | 1 | Контрольная работа «Начальные геометрические сведения». | Уметь применять изученный теоретический материал при выполнении письменной работы
| самостоятельно выбирать рациональный способ решения. |
|
|
|
|
|
|
| Линейная функция (17 часов) |
| 31 | 1 | Координатная плоскость | Б: Научить: - понимать и использовать функциональные понятия и язык (термины, символические обозначения); - строить графики линейных функций; исследовать свойства линейных функций на основе поведения их графиков; - понимать функцию как важнейшую математическую модель для описания процессов и явлений окружающего мира. П: дать возможность: - проводить исследования, связанные с изучением свойств функций, в том числе с использованием компьютера; на основе графиков изученных функций строить более сложные графики; - использовать функциональные представления и свойства функций для решения математических задач из различных разделов математики.
| находить координаты точки на плоскости, отмечать точку с заданными координатами, используя алгоритм построения точки в прямоугольной системе координат, строить прямую, удовлетворяющую заданному уравнению. |
|
|
|
|
| 32 | 1 | Решение задач по теме: «Координатная плоскость». | Строить на координатной плоскости геометрические фигуры, находить координаты некоторых точек фигуры. |
|
|
|
|
| 33 | 1 | Решение задач по теме: «Координатная плоскость». | Строить на координатной плоскости точки и фигуры по заданным координатам; определять координаты точек. |
|
|
|
|
| 34 | 1 | Линейное уравнение с двумя переменными и его график. | определять, является ли пара чисел решением линейного уравнения с двумя переменными, строить график уравнения ax+by+c=0,находить точку пересечения графиков линейных уравнений, выражать в линейном уравнении одну переменную через другую; |
|
|
|
|
| 35 | 1 | Решение задач по теме: «Линейное уравнение с двумя переменными и его график». | Знать понятия линейная функция, независимая переменная (аргумент), зависимая переменная, график линейной функции |
|
|
|
|
| 36 | 1 | Решение задач по теме: «Линейное уравнение с двумя переменными и его график». | Определять, является ли пара чисел решением данного уравнения с двумя переменными; приводить примеры решений уравнений с двумя переменными; решать задачи, алгебраической моделью которых является уравнение с двумя переменными; находить целые решения путем перебора. |
|
|
|
|
| 37 | 1 | Самостоятельная работа по теме: «Линейное уравнение с двумя переменными и его график» | Знать понятия линейная функция, независимая переменная (аргумент), зависимая переменная, график линейной функции. |
|
|
|
|
| 38 | 1 | Линейная функция и его график. | определять по формуле характер монотонности, преобразовывать линейное уравнение к виду линейной функции y=kx+m, находить значение функции при заданном значении аргумента и обратно |
|
|
|
|
| 39 | 1 | Решение задач по теме: «Линейная функция и её график».
| Вычислять значения линейных функций, составлять таблицы значений функции. Строить график линейной функции, описывать ее свойства на основе графических представлений. |
|
|
|
|
| 40 | 1 | Самостоятельная работа по теме: «Линейная функция и её график» | Уметь определять по формуле характер монотонности, преобразовывать линейное уравнение к виду линейной функции y=kx+m, находить значение функции при заданном значении аргумента и обратно, строить график линейной функции; находить координаты точек пересечения графика с координатными осями, координаты точки пересечения графиков |
|
|
|
|
| 41 | 1 | Линейная функция и его график. | определять по формуле характер монотонности, преобразовывать линейное уравнение к виду линейной функции y=kx+m, находить значение функции при заданном значении аргумента и обратно |
|
|
|
|
| 42 | 1 | Линейная функция у= кх. | находить коэффициент пропорциональности, строить график функции y=kx, определять знак углового коэффициента по графику. |
|
|
|
|
| 43 | 1 | Решение задач по теме: «Линейная функция у = кх». | находить коэффициент пропорциональности, строить график функции y=kx, определять знак углового коэффициента по графику. |
|
|
|
|
| 44 | 1 | Линейная функция у = кх. Самостоятельная работа | находить коэффициент пропорциональности, строить график функции y=kx, определять знак углового коэффициента по графику. |
|
|
|
|
| 45 | 1 | Взаимное расположение графиков линейных функций. | расширять и обобщать знания о построении графика линейной функции, исследовать взаимное расположение графиков линейных функций. |
|
|
|
|
| 46 | 1 | Решение задач по теме: «линейная функция». | выбирать эффективные способы решения учебных задач на основе заданных алгоритмов, применять изученные алгоритмы при решении практических задач. |
|
|
|
|
| 47 | 1 | Контрольная работа по теме: «Линейная функция». | Уметь применять изученный теоретический материал при выполнении письменной работы | самостоятельно выбирать рациональный способ решения задач. |
|
|
|
|
|
|
| Система двух линейных уравнений с двумя переменными (15 часов) |
|
|
|
|
| 48 | 1 | Системы двух линейных уравнений с двумя переменными. Основные понятия. | Б: Научить: - решать систем двух уравнений с двумя переменными; - применять графические представления для исследования и решения систем уравнений с двумя переменными; - решать задачи с помощью систем уравнений. П: дать возможность: - овладеть специальными приемами решения систем уравнений; уверенно применять аппарат уравнений для решения разнообразных задач из математики, смежных предметов, практики; - применять графические представления для исследования систем уравнений, содержащих буквенные коэффициенты | определять, является ли пара чисел решением системы уравнений, решать систему линейных уравнений графическим способом |
|
|
|
|
| 49 | 1 | Графический метод решения систем уравнений. | объяснять, почему система не имеет решений, имеет единственное решение, имеет бесконечное множество решений. |
|
|
|
|
| 50 | 1 | Решение систем уравнений графическим методом. | определять, является ли пара чисел решением системы уравнений, решать систему линейных уравнений графическим способом, объяснять, почему система не имеет решений, имеет единственное решение |
|
|
|
|
| 51 | 1 | Метод подстановки. | решать системы двух линейных уравнений методом подстановки по алгоритму; |
|
|
|
|
| 52 | 1 | Решение систем уравнений методом подстановки | решать системы двух линейных уравнений методом подстановки по алгоритму |
|
|
|
|
| 53 | 1 | Решение систем уравнений методом подстановки. | составлять математическую модель реальной ситуации в виде системы линейных уравнений. |
|
|
|
|
| 54 | 1 | Метод алгебраического сложения. | решать системы двух линейных уравнений методом алгебраического сложения по алгоритму |
|
|
|
|
| 55 | 1 | Решение систем уравнений методом алгебраического сложения. | решать системы двух линейных уравнений методом алгебраического сложения по алгоритму, составлять математическую модель реальной ситуации в виде системы линейных уравнений. |
|
|
|
|
| 56 | 1 | Самостоятельная работа по теме: «Метод алгебраического сложения». | Решать текстовые задачи алгебраическим способом: переходить от словесной формулировки условия задачи к алгебраической модели путем составления системы уравнений; решать составленную систему уравнений; интерпретировать результат. |
|
|
|
|
| 57 | 1 | Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций | решать текстовые задачи с помощью системы линейных уравнений с двумя переменными на движение по дороге |
|
|
|
|
| 58 | 1 | Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций | решать текстовые задачи с помощью системы линейных уравнений с двумя переменными на движение по дороге, части, на числовые величины и проценты. |
|
|
|
|
| 59 | 1 | Решений задач с помощью систем уравнений. | Исследовать системы уравнений с двумя переменными, содержащие буквенные коэффициенты. Конструировать эквивалентные речевые высказывания с использованием алгебраического и геометрического языков. Использовать функционально-графические представления для решения и исследования систем уравнений. |
|
|
|
|
| 60 | 1 | Решений задач с помощью систем уравнений. | Исследовать системы уравнений с двумя переменными, содержащие буквенные коэффициенты. Конструировать эквивалентные речевые высказывания с использованием алгебраического и геометрического языков. Использовать функционально-графические представления для решения и исследования систем уравнений. |
|
|
|
|
| 61 | 1 | Обобщающий урок по теме «Системы двух линейных уравнений с двумя переменными». | Решать системы двух линейных уравнений с двумя переменными графически, методом подстановки, методом алгебраического сложения.
|
|
|
|
|
| 62 | 1 | Контрольная работа по теме: «Системы двух линейных уравнений с двумя переменными». | Уметь применять изученный теоретический материал при выполнении письменной работы | самостоятельно действовать в ситуации неопределенности при решении актуальных для них проблем. |
|
|
|
|
|
|
| Треугольники (18 часов) |
|
|
|
|
| 63 | 1 | Треугольник | Б: Научить: - пользоваться языком геометрии для описания предметов окружающего мира и их конфигурации; - распознавать и изображать на чертежах и рисунках геометрические фигуры и их конфигурации; - находить значения длин линейных элементов фигур, градусную меру углов от 0º до 180º, применяя определения, свойства и признаки фигур и их элементов; - решать задачи на доказательство, опираясь на изученные свойства фигур и применяя изученные методы доказательства; - решать несложные задачи на построение, применяя основные алгоритмы построения с помощью циркуля и линейки. П: дать возможность: - приобрести опыт применения алгебраического аппарата при решении геометрических задач. | Называть элементы треугольника, распознавать равные треугольники |
|
|
|
|
| 64 | 1 | Первый признак равенства треугольников. | Иметь понятие теоремы и доказательства теоремы, доказать 1 признак равенства треугольников. |
|
|
|
|
| 65 | 1 | Первый признак равенства треугольников. | Называть элементы треугольника, решать задачи на применение 1 признака равенства треугольников. |
|
|
|
|
| 66 | 1 | Перпендикуляр к прямой | Доказывать теорему о перпендикуляре |
|
|
|
|
| 67 | 1 | Медианы, биссектрисы и высоты треугольника | Строить медианы, биссектрисы и высоты треугольника |
|
|
|
|
| 68 | 1 | Медианы, биссектрисы и высоты треугольника | Строить медианы, биссектрисы и высоты треугольника |
|
|
|
|
| 69 | 1 | Свойства равнобедренного треугольника. | Доказывать теоремы о свойствах равнобедренного треугольника, применять его при решении задач. |
|
|
|
|
| 70 | 1 | Свойства равнобедренного треугольника. | Доказывать теоремы о свойствах равнобедренного треугольника, применять его при решении задач. |
|
|
|
|
| 71 | 1 | Второй признак равенства треугольников. | доказать 2 признак равенства треугольников. Применять признаки при решении задач. |
|
|
|
|
| 72 | 1 | Третий признак равенства треугольников | Доказывать 3 признак равенства треугольников. Применять признаки при решении задач. |
|
|
|
|
| 73 | 1 | Второй и третий признаки равенства треугольников | Применять признаки при решении задач.
|
|
|
|
|
| 74 | 1 | Второй и третий признаки равенства треугольников | Применять признаки при решении задач.
|
|
|
|
|
| 75 | 1 | Окружность | Строить радиус, хорду, диаметр окружности. Распознавать эти элементы на рисунке |
|
|
|
|
| 76 | 1 | Задачи на построение. | Выполнять простейшие построения: отрезка, равного данному; угла, равного данному; биссектрисы данного угла; прямой, проходящей через данную точку и перпендикулярной к данной прямой; середины отрезка. |
|
|
|
|
| 77 | 1 | Задачи на построение. | Выполнять простейшие построения: отрезка, равного данному; угла, равного данному; биссектрисы данного угла; прямой, проходящей через данную точку и перпендикулярной к данной прямой; середины отрезка. |
|
|
|
|
| 78 | 1 | Решение задач. | Применять признаки при решении задач. |
|
|
|
|
| 79 | 1 | Решение задач | Применять признаки при решении задач. |
|
|
|
|
| 80 | 1 | Контрольная работа «Треугольники» | Уметь применять изученный теоретический материал при выполнении письменной работы | Решение задач на применение признаков равенства треугольников и задач на построение. |
|
|
|
|
|
|
| Степень с натуральным показателем и ее свойства (9 часов) |
|
|
|
|
| 81 | 1 | Что такое степень с натуральным показателем. | Б: Научить: - выражать числа в эквивалентной форме, выбирая наиболее подходящую в зависимости от конкретной ситуации; - выполнять преобразования выражений, содержащих степени с целым показателем. П: дать возможность: - научиться использовать приемы, рационализирующие вычисления, приобрести привычку контролировать вычисления, выбирая подходящий для ситуации способ; - применять тождественные преобразования для решения задач из различных разделов курса. | Формулировать определение степени с натуральным показателем |
|
|
|
|
| 82 | 1 | Степень с натуральным показателем. | возводить числа в степень; находить значение сложных выражений со степенями, представлять число в виде произведения степеней. |
|
|
|
|
| 83 | 1 | Таблица основных степеней. | пользоваться таблицей степеней при выполнении вычислений со степенями. |
|
|
|
|
| 84 | 1 | Таблица основных степеней | пользоваться таблицей степеней при выполнении вычислений со степенями. |
|
|
|
|
| 85 | 1 | Свойства степени с натуральными показателями. | формулировать, записывать в символической форме и обосновывать свойства степени с целым неотрицательным показателем; применять свойства степени для преобразования выражений и вычислений. |
|
|
|
|
| 86 | 1 | Решение задач по теме: «Свойства степени с натуральными показателями». | формулировать, записывать в символической форме и обосновывать свойства степени с целым неотрицательным показателем; |
|
|
|
|
| 87 | 1 | Умножение и деление степеней с одинаковыми показателями. | применять правила умножения и деления степеней с одинаковыми показателями для упрощения числовых и алгебраических выражений и сложных алгебраических дробей. |
|
|
|
|
| 88 | 1 | Решение задач по теме: «Умножение и деление степеней с одинаковыми показателями». | Воспроизводить формулировки и доказательства изученных теорем. Конструировать математические предложения с помощью связок если…, то…, |
|
|
|
|
| 89 | 1 | Степень с нулевым показателем. | Формулировать определение степени с натуральным показателем, с нулевым показателем; применять свойства степени для преобразования выражений и вычислений. Воспроизводить формулировки определений, конструировать несложные определения самостоятельно. |
|
|
|
|
|
|
| Одночлены. Арифметические операции над одночленами (8 часов) |
|
|
|
|
| 90 | 1 | Понятие одночлена. Стандартный вид одночлена. | Б: Научить: - выполнять преобразования выражений, содержащих степени с целым показателем. П: дать возможность: - применять тождественные преобразования для решения задач из различных разделов курса. | находить значение одночлена при указанных значениях переменных; приводить к стандартному виду сложные одночлены. |
|
|
|
|
| 91 | 1 | Сложение и вычитание одночленов. | применять правила сложения и вычитания одночленов для упрощения выражений и решения уравнений. |
|
|
|
|
| 92 | 1 | Самостоятельная работа по теме: «Сложение и вычитание одночленов». | Выполнять действия с одночленами. |
|
|
|
|
| 93 | 1 | Умножение одночленов. Возведение одночлена в натуральную степень | применять правила умножения одночленов и возведения одночлена в натуральную степень для упрощения выражений |
|
|
|
|
| 94 | 1 | Решение задач по теме: «Умножение одночленов». | Выполнять действия с одночленами. |
|
|
|
|
| 95 | 1 | Деление одночлена на одночлен | выполнять деление одночленов по алгоритму; применять правило деления одночленов для упрощения алгебраических дробей. |
|
|
|
|
| 96 | 1 | Решение задач по теме: «Деление одночлена на одночлен». | самостоятельно действовать в ситуации неопределенности при решении актуальных для них проблем. |
|
|
|
|
| 97 | 1 | Контрольная работа по теме: «Одночлены. Арифметические операции над одночленами». | Уметь применять изученный теоретический материал при выполнении письменной работы | Выполнять действия с одночленами. Самостоятельно выбирать рациональный способ решения задач. |
|
|
|
|
|
|
| Параллельные прямые (13 часов) |
|
|
|
|
| 98 | 1 | Определение параллельных прямых | Б: Научить: - пользоваться языком геометрии для описания предметов окружающего мира и их конфигурации; - распознавать и изображать на чертежах и рисунках геометрические фигуры и их конфигурации; - находить градусную меру углов от 0º до 180º, применяя определения, свойства и признаки фигур и их элементов; - решать задачи на доказательство, опираясь на изученные свойства фигур и применяя изученные методы доказательства. П: дать возможность: - приобрести опыт применения алгебраического аппарата при решении геометрических задач; - овладеть методом от противного для решения задач на доказательство. | Строить параллельные прямые, обозначать соответствующими буквами |
|
|
|
|
| 99 | 1 | Признаки параллельности двух прямых. | Показывать на рисунке пары накрест лежащих, соответственных, односторонних углов, доказывать признаки параллельности прямых, строить параллельные прямые с помощью угольника и линейки. |
|
|
|
|
| 100 | 1 | Признаки параллельности двух прямых. | Показывать на рисунке пары накрест лежащих, соответственных, односторонних углов, доказывать признаки параллельности прямых, строить параллельные прямые с помощью угольника и линейки. |
|
|
|
|
| 101 | 1 | Признаки параллельности двух прямых. | Показывать на рисунке пары накрест лежащих, соответственных, односторонних углов, доказывать признаки параллельности прямых, строить параллельные прямые с помощью угольника и линейки. |
|
|
|
|
| 102 | 1 | Аксиома параллельных прямых. | Применять аксиому и следствия при решении задач, свойства параллельных прямых. |
|
|
|
|
| 103 | 1 | Аксиома параллельных прямых. | Применять аксиому и следствия при решении задач, свойства параллельных прямых. |
|
|
|
|
| 104 | 1 | Свойства параллельных прямых | Применять свойства параллельных прямых при решении задач. |
|
|
|
|
| 105 | 1 | Свойства параллельных прямых | Применять свойства параллельных прямых при решении задач. |
|
|
|
|
| 106 | 1 | Решение задач по теме: «Свойства параллельных прямых» | Применять свойства параллельных прямых при решении задач. |
|
|
|
|
| 107 | 1 | Решение задач по теме: «Признаки параллельности двух прямых» | Применять признаки параллельных прямых при решении задач. |
|
|
|
|
| 108 | 1 | Решение задач по теме: «Параллельные прямые» | Решать задачи на применение признаков и свойств параллельных прямых. |
|
|
|
|
| 109 | 1 | Решение задач по теме: «Параллельные прямые» | Решать задачи на применение признаков и свойств параллельных прямых |
|
|
|
|
| 110 | 1 | Контрольная работа «Параллельность прямых». | Уметь применять изученный теоретический материал при выполнении письменной работы | Решать задачи на применение признаков и свойств параллельных прямых |
|
|
|
|
|
|
| Многочлены. Арифметические операции над одночленами (18 часов) |
|
|
|
|
| 111 | 1 | Многочлены. Основные понятия. | Б: Научить: - решать задачи, содержащие буквенные данные; работать с формулами; - выполнять преобразования выражений, содержащих степени с целым показателем; - выполнять тождественные преобразования рациональных выражений на основе правил действий над многочленами. П: дать возможность: - научиться выполнять многошаговые преобразования рациональных выражений, применяя широкий набор способов и приемов; - применять тождественные преобразования для решения задач из различных разделов курса. | приводить сложный многочлен к стандартному виду, записывать его члены в порядке убывания степеней переменной и находить, при каких значениях переменной он равен 1 |
|
|
|
|
| 112 | 1 | Стандартный вид многочлена. | приводить сложный многочлен к стандартному виду, записывать его члены в порядке убывания степеней переменной и находить, при каких значениях переменной он равен 1 |
|
|
|
|
| 113 | 1 | Сложение и вычитание многочленов | выполнять сложение и вычитание многочленов, преобразуя в многочлен стандартного вида, решать уравнения. |
|
|
|
|
| 114 | 1 | Закрепление знаний по теме: «Сложение и вычитание многочленов». | Выполнять действия с многочленами. Применять различные формы самоконтроля при выполнении преобразований. |
|
|
|
|
| 115 | 1 | Умножение многочлена на одночлен. | выполнять умножение многочлена на одночлен, выносить за скобки одночленный множитель. |
|
|
|
|
| 116 | 1 | Решение задач по теме: «Умножение многочлена на одночлен». | выполнять умножение многочлена на одночлен, выносить за скобки одночленный множитель. |
|
|
|
|
| 117 | 1 | Самостоятельная работа по теме: «Умножение многочлена на одночлен». | Выполнять действия с многочленами. Применять различные формы самоконтроля при выполнении преобразований. |
|
|
|
|
| 118 | 1 | Умножение многочлена на многочлен. | выполнять умножение многочленов, решать текстовые задачи, математическая модель которых содержит произведение многочленов. |
|
|
|
|
| 119 | 1 | Решение задач по теме: «Умножение многочлена на многочлен». | выполнять умножение многочленов, решать текстовые задачи, математическая модель которых содержит произведение многочленов. |
|
|
|
|
| 120 | 1 | Решение задач по теме: «Многочлены. Арифметические операции над многочленами». | выполнять умножение многочленов, решать текстовые задачи. |
|
|
|
|
| 121 | 1 | Формулы сокращенного умножения. Квадрат суммы и квадрат разности. | Выводить формулы сокращенного умножения, применять их в преобразованиях выражений и вычислениях. |
|
|
|
|
| 122 | 1 | Решение задач по теме: «Квадрат суммы и квадрат разности». | выполнять преобразования многочленов по формулам квадрата суммы и разности, применять ФСУ для упрощения выражений, решения уравнений. |
|
|
|
|
| 123 | 1 | Разность квадратов. | Выводить формулы сокращенного умножения, применять их в преобразованиях выражений и вычислениях. |
|
|
|
|
| 124 | 1 | Решение задач по теме: «Разность квадратов» | выполнять преобразования многочленов по формулам квадрата суммы и разности, разности квадратов и применять ФСУ для упрощения выражений, решения уравнений |
|
|
|
|
| 125 | 1 | Разность кубов и сумма кубов. | выполнять преобразования многочленов по формулам квадрата суммы и разности, разности квадратов и кубов, суммы кубов; применять ФСУ для упрощения выражений, решения уравнений |
|
|
|
|
| 126 | 1 | Деление многочлена на одночлен. | делить многочлен на одночлен; использовать правило деления многочлена на одночлен для упрощения выражений, решения уравнений. |
|
|
|
|
| 127 | 1 | Деление многочлена на одночлен. | определять адекватные способы решения учебной задачи на основе заданных алгоритмов. |
|
|
|
|
| 128 | 1 | Контрольная работа по теме: «Многочлены» | Уметь применять изученный теоретический материал при выполнении письменной работы | расширять и обобщать знания о сложении, вычитании, умножении и делении многочленов, вывода и применения ФСУ. |
|
|
|
|
|
|
| Соотношение между сторонами и углами треугольника (6 часов) |
|
|
|
|
| 129 | 1 | Теорема о сумме углов треугольника. | Б: Научить: - пользоваться языком геометрии для описания предметов окружающего мира и их конфигурации; - распознавать и изображать на чертежах и рисунках геометрические фигуры и их конфигурации; - находить градусную меру углов от 0º до 180º, применяя определения, свойства и признаки фигур и их элементов; - решать задачи на доказательство, опираясь на изученные свойства фигур и применяя изученные методы доказательства; - решать несложные задачи на построение, применяя основные алгоритмы построения с помощью циркуля и линейки. П: дать возможность: - приобрести опыт применения алгебраического аппарата при решении геометрических задач; - овладеть методом от противного для решения задач на доказательство; - овладеть традиционной схемой решения задач на построение с помощью циркуля и линейки: анализ, построение, доказательство, исследование; - приобрести опыт исследования свойств планиметрических фигур с помощью компьютерных программ. | Доказывать и применять при решении задач теорему о сумме углов треугольника и её следствия. |
|
|
|
|
| 130 | 1 | Остроугольный, прямоугольный и тупоугольный треугольники. | Распознавать треугольники по углам, применять на практике | тест |
|
|
|
| 131 | 1 | Теорема о соотношениях между сторонами и углами треугольника. | Доказывать теорему, применять её при решении задач, следствия. |
|
|
|
|
| 132 | 1 | Теорема о соотношениях между сторонами и углами треугольника. | Доказывать теорему, применять её при решении задач, следствия. |
|
|
|
|
| 133 | 1 | Неравенство треугольника. | Применять теорему о неравенстве треугольников при решении задач |
|
|
|
|
| 134 | 1 | Контрольная работа по теме: «Соотношения между сторонами и углами треугольника». | Уметь применять изученный теоретический материал при выполнении письменной работы |
|
|
|
|
|
|
|
| Разложение многочленов на множители (22 часа) |
|
|
|
|
| 135 | 1 | Что такое разложение многочленов на множители и зачем оно нужно. | Б: Научить: -владеть понятиями «тождество», «тождественное преобразование», решать задачи, содержащие буквенные данные; работать с формулами; - выполнять преобразования выражений, содержащих степени с целым показателем; - выполнять тождественные преобразования рациональных выражений на основе правил действий над многочленами; - выполнять разложение многочленов на множители. П: дать возможность: - научиться выполнять многошаговые преобразования рациональных выражений, применяя широкий набор способов и приемов; - применять тождественные преобразования для решения задач из различных разделов курса. | решать уравнения и сокращать дробь, разложив на множители. |
|
|
|
|
| 136 | 1 | Вынесение общего множителя за скобки. | выполнять вынесение общего множителя за скобки по алгоритму; применять прием вынесения общего множителя за скобки для упрощения вычислений, решения уравнений. |
|
|
|
|
| 137 | 1 | Решение задач по теме: «Вынесение общего множителя за скобки». | Выполнять разложение многочлена на множители и сокращение алгебраических дробей. Применять различные формы самоконтроля при выполнении преобразований. |
|
|
|
|
| 138 | 1 | Способ группировки. | выполнять разложение многочлена на множители способом группировки по алгоритму; выполнять разложение трехчлена на множители способом группировки; |
|
|
|
|
| 139 | 1 | Решение задач по теме: «Способ группировки». | выполнять разложение многочлена на множители способом группировки по алгоритму; выполнять разложение трехчлена на множители способом группировки; |
|
|
|
|
| 140 | 1 | Самостоятельная работа по теме: «Способ группировки». | решать уравнения, разложив на множители способом группировки. |
|
|
|
|
| 141 | 1 | Разложение многочленов на множители с помощью формул сокращенного умножения. | раскладывать многочлен на множители с помощью ФСУ; применять прием разложения многочлена на множители с помощью ФСУ для упрощения вычислений, решения уравнений. |
|
|
|
|
| 142 | 1 | Решение задач по теме: «Разложение многочленов на множители с помощью формул сокращенного умножения». | раскладывать многочлен на множители с помощью ФСУ; применять прием разложения многочлена на множители с помощью ФСУ для упрощения вычислений, решения уравнений. |
|
|
|
|
| 143 | 1 | Решение задач по теме: «Разложение многочленов на множители с помощью формул сокращенного умножения». | раскладывать многочлен на множители с помощью ФСУ; применять прием разложения многочлена на множители с помощью ФСУ для упрощения вычислений, решения уравнений. |
|
|
|
|
| 144 | 1 | Самостоятельная работа по теме: «Разложение многочленов на множители с помощью формул сокращенного умножения». | Выполнять разложение многочлена на множители с помощью формул сокращенного умножения. Применять различные формы самоконтроля при выполнении преобразований. |
|
|
|
|
| 145 | 1 | Решение задач по теме: «Разложение многочленов на множители с помощью формул сокращенного умножения». | Выполнять разложение многочлена на множители с помощью формул сокращенного умножения. Применять различные формы самоконтроля при выполнении преобразований. |
|
|
|
|
| 146 | 1 | Разложение многочленов на множители с помощью комбинации различных приемов. | выполнять разложение многочлена на множители с помощью комбинации изученных приемов; применять разложение многочлена на множители с помощью комбинации изученных приемов для упрощения вычислений, решения уравнений |
|
|
|
|
| 147 | 1 | Решение задач по теме: «Разложение многочленов на множители с помощью комбинации различных приемов». | выполнять разложение многочлена на множители с помощью комбинации изученных приемов; применять разложение многочлена на множители с помощью комбинации изученных приемов для упрощения вычислений, решения уравнений |
|
|
|
|
| 148 | 1 | Самостоятельная работа по теме: «Разложение многочленов на множители с помощью комбинации различных приемов». | выполнять разложение многочлена на множители с помощью комбинации изученных приемов; применять разложение многочлена на множители с помощью комбинации изученных приемов для упрощения вычислений, решения уравнений |
|
|
|
|
| 149 | 1 | Сокращение алгебраических дробей. | сокращать алгебраические дроби, раскладывая выражения на множители, применяя комбинации изученных приемов. |
|
|
|
|
| 150 | 1 | Решение задач по теме: «Сокращение алгебраических дробей». | сокращать алгебраические дроби, раскладывая выражения на множители, применяя комбинации изученных приемов. |
|
|
|
|
| 151 | 1 | Решение задач по теме: «Сокращение алгебраических дробей». | Выполнять разложение многочлена на множители и сокращение алгебраических дробей. Применять различные формы самоконтроля при выполнении преобразований. |
|
|
|
|
| 152 | 1 | Самостоятельная работа по теме: «Сокращение алгебраических дробей». | Выполнять разложение многочлена на множители и сокращение алгебраических дробей. Применять различные формы самоконтроля при выполнении преобразований. |
|
|
|
|
| 153 | 1 | Решение задач по теме: «Сокращение алгебраических дробей». | сокращать алгебраические дроби, раскладывая выражения на множители, применяя комбинации изученных приемов. |
|
|
|
|
| 154 | 1 | Тождества. | доказывать простейшие тождества. |
|
|
|
|
| 155 | 1 | Решение задач по теме: «Тождества». | доказывать простейшие тождества, применяя комбинации изученных приемов. |
|
|
|
|
| 156 | 1 | Контрольная работа по теме: «Разложение многочленов на множители». | Уметь применять изученный теоретический материал при выполнении письменной работы | расширять и обобщать знания о вынесении общего множителя за скобки, группировки слагаемых, преобразовывать выражения, используя ФСУ, выделение полного квадрата. |
|
|
|
|
|
|
| Прямоугольные треугольники 12 часов |
|
|
|
|
| 157 | 1 | Некоторые свойства прямоугольных треугольников. | Б: Научить: - пользоваться языком геометрии для описания предметов окружающего мира и их конфигурации; - распознавать и изображать на чертежах и рисунках геометрические фигуры и их конфигурации; - находить градусную меру углов от 0º до 180º, применяя определения, свойства и признаки фигур и их элементов; - решать задачи на доказательство, опираясь на изученные свойства фигур и применяя изученные методы доказательства; - решать несложные задачи на построение, применяя основные алгоритмы построения с помощью циркуля и линейки. П: дать возможность: - приобрести опыт применения алгебраического аппарата при решении геометрических задач; - овладеть методом от противного для решения задач на доказательство; - овладеть традиционной схемой решения задач на построение с помощью циркуля и линейки: анализ, построение, доказательство, исследование; - приобрести опыт исследования свойств планиметрических фигур с помощью компьютерных программ. | Свойства прямоугольных треугольников |
|
|
|
|
| 158 | 1 | Некоторые свойства прямоугольных треугольников. |
|
|
|
|
| 159 | 1 | Признаки равенства прямоугольных треугольников. | Признаки равенства прямоуг. треугольников |
|
|
|
|
| 160 | 1 | Признаки равенства прямоугольных треугольников. |
|
|
|
|
| 161 | 1 | Расстояние от точки до прямой. Расстояние между параллельными прямыми. | Расстояние от точки до прямой |
|
|
|
|
| 162 | 1 | Построение треугольника по трем элементам. | План построения треугольника по трем элементам |
|
|
|
|
| 163 | 1 | Задачи на построение |
|
|
|
|
| 164 | 1 | Задачи на построение |
|
|
|
|
| 165 | 1 | Решение задач по теме: «Прямоугольные треугольники. Построение треугольника по трем элементам» |
|
|
|
|
|
| 166 | 1 | Решение задач. Прямоугольные треугольники. |
|
|
|
|
|
| 167 | 1 | Решение задач |
|
|
|
|
|
| 168 | 1 | Контрольная работа по теме: «Прямоугольные треугольники» | Уметь применять изученный теоретический материал при выполнении письменной работы |
|
|
|
|
|
| Функция у=х2 (11 часов) |
| 169 | 1 | Функция у=х2 и ее график. | Б: Научить: - понимать и использовать функциональные понятия и язык (термины, символические обозначения); - строить графики функций y=x² и y= –x², исследовать свойства этих функций на основе поведения их графиков; - понимать функцию как важнейшую математическую модель для описания процессов и явлений окружающего мира. П: дать возможность: - проводить исследования, связанные с изучением свойств функций, в том числе с использованием компьютера; на основе графиков изученных функций строить более сложные графики; - использовать функциональные представления и свойства функций для решения математических задач из различных разделов математики. | Построение квадратичной функции. Парабола её элементы, функция у=х2 |
|
|
|
|
| 170 | 1 | Функция у=х2 и ее график. |
|
|
|
|
| 171 | 1 | Решение задач по теме: «Функция у=х2 и ее график». |
|
|
|
|
| 172 | 1 | Решение задач по теме: «Функция у=х2 и ее график». |
|
|
|
|
| 173 | 1 | Графическое решение уравнений. | Алгоритм графического решения уравнения. Примеры решения уравнений графи-ческим способом. |
|
|
|
|
| 174 | 1 | Решение задач по теме: «Графическое решение уравнений». |
|
|
|
|
| 175 | 1 | Решение задач по теме: «Графическое решение уравнений». |
|
|
|
|
| 176 | 1 | Что означает в математике запись у=f(х) | Понятие функции. Смысл записи у= f(х), кусочная функция, область определения функции, непрерывность функции |
|
|
|
|
| 177 | 1 | Решение задач по теме: «Что означает в математике запись у=f(х)» |
|
|
|
|
| 178 | 1 | Решение задач по теме: «Что означает в математике запись у=f(х)» |
|
|
|
|
| 179 | 1 | Контрольная работа по теме: «Функция у=х2». | Уметь применять изученный теоретический материал при выполнении письменной работы | Сокращение дробей. Графи-ческое решение уравнений. Наи-большее и наи-меньшее значе-ния функции |
|
|
|
|
| Элементы статистической обработки данных (7 часов) |
| 180 | 1 | Данные и ряды данных |
|
|
|
|
|
|
| 181 | 1 | Упорядоченные ряды данных. Таблица распределения |
|
|
|
|
|
|
| 182 | 1 | Нечисловые ряды данных |
|
|
|
|
|
|
| 183 | 1 | Составление таблиц распределения без упорядочивания данных. |
|
|
|
|
|
|
| 184 | 1 | Частота результата таблица распределения частот |
|
|
|
|
|
|
| 185 | 1 | Процентные частоты. Таблицы распределения частот в процентах |
|
|
|
|
|
|
| 186 | 1 | Группировка данных |
|
|
|
|
|
|
| Повторение (19 часов) |
| 187 | 1 | Числовые и алгебраические выражения. |
|
|
|
|
|
|
| 188 | 1 | Графики функций. | - основные понятия темы; алгоритмы построения и чтения графиков: - приёмы использования графиков для решения уравнений, систем уравнений, неравенств. Уметь: - переводить информацию из одной знаковой системы в другую; приводить для иллюстрации изученных положений самостоятельно подобранные примеры; - владеть навыками совместной деятельности, распределять работу в группе, оценивать работу участников группы | Систематизация знаний по темам: «Линейная функция» и «Функция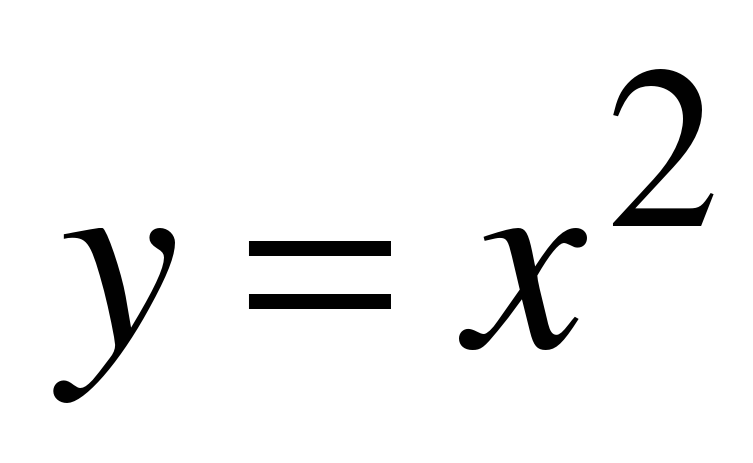 » » |
|
|
|
|
| 189 | 1 | Линейные уравнения и системы уравнений. | Знать: - алгоритмы решения системы двух линейных уравнений с двумя переменными методом алгебраического сложения и методом подстановки; - приёмы рационального решения систем двух линейных уравнений с двумя переменными Уметь: -решать комбинированные задачи с использованием 2-3 и более алгоритмов, использовать приёмы рационального решения задач; распределять работу в группе, оценивать работу участников группы | Систематизация знаний по теме: «Системы двух линейных уравнений с двумя переменными». Устранение пробелов в знаниях учащихся. |
|
|
|
|
| 190 | 1 | Многочлены. | Знать: - основные понятия темы; алгоритмы основных операций над одночленами и многочленами; - приёмы рационального выполнения действий с одночленами и многочленами. Уметь: Решать комбинированные задачи с использованием более чем 3 алгоритмов; использовать приёмы рационального решения задач; приводить для иллюстрации изученных положений самостоятельно подобранные примеры | Систематизация знаний по темам: «Одночлены» и «Многочлены». Устранение пробелов в знаниях учащихся. Подготовка к итоговой контрольной работе |
|
|
|
|
| 191 | 1 | Алгебраические дроби. |
|
|
|
|
| 192 | 1 | Решение уравнений. |
|
|
|
|
| 193 | 1 | Решение неравенств. |
|
|
|
|
| 194 | 1 | Решение задач. |
|
|
|
|
| 195 | 1 | Итоговая контрольная работа №15 |
|
|
|
|
| 196 | 1 | Анализ контрольной работы. |
|
|
|
|
|
|
| 197 | 1 | Свойства равнобедренного треугольника | Знать основные теоремы темы, уметь применять при доказательствах. | Применять свойства равнобедренного треугольника при решении задач. |
|
|
|
|
| 198 | 1 | Признаки равенства треугольников | Знать основные теоремы темы, уметь применять при доказательствах. | Применять признаки при решении задач. |
|
|
|
|
| 199 | 1 | Признаки равенства треугольников |
|
|
|
|
| 200 | 1 | Признаки параллельности прямых | Знать признаки параллельности прямых, уметь применять при решении задач. |
|
|
|
|
|
| 201 | 1 | Признаки параллельности прямых |
|
|
|
|
|
| 202 | 1 | Решение задач | Знать: - основные понятия темы. Уметь: Решать задачи. |
|
|
|
|
|
| 203 | 1 | Итоговая контрольная работа по геометрии |
|
|
|
|
|
|
| 204 | 1 | Итоговый урок. |
|
|
|
|
|
|
НОРМЫ ОЦЕНКИ ЗУН ОБУЧАЮЩИХСЯ
Учитель, опираясь на эти рекомендации, оценивает знания и умения учащихся с учетом их индивидуальных особенностей.
1. Содержание и объем материала, подлежащего проверке, определяется программой по математике для средней школы. При проверке усвоения этого материала следует выявлять полноту, прочность усвоения учащимися теории применять ее на практике в знакомых и незнакомых ситуациях.
2. Основными формами проверки знаний и умений учащихся по математике в средней школе письменная контрольная работа и устный опрос.
При оценке письменных и устных ответов учитель в первую очередь учитывает показанные учащимися знания и умения (их полноту, глубину, прочность, использование в различных ситуациях). Оценка зависит также от наличия и характера погрешностей, допущенных учащимися.
3. Среди погрешностей выделяются ошибки и недочеты:
Погрешность считается ошибкой, если она свидетельствует о том, что ученик не овладел знаниями, умениями, указанными в программе.
К недочетам относятся погрешности, свидетельствующие о недостаточно полном или недостаточно прочном усвоении основных знаний, умений или об отсутствии знаний, не считающихся в соответствии с программой основными. Недочетами также являются: погрешности, которые не привели к искажению смысла полученного учеником задания или способа его выполнения; неаккуратная запись; небрежное выполнение чертежа.
Граница между ошибками и недочетами является в некоторой степени условной. При одних обстоятельствах допущенная учащимися погрешность может рассматриваться учителем как ошибка, в другое время и при других обстоятельствах – как недочет.
4. Задания для устного и письменного опроса учащихся состоят из теоретических вопросов и задач.
Ответ не теоретический вопрос считается безупречным, если по своему содержанию полностью соответствует вопросу, содержит все необходимые теоретические факты и обоснованные выводы, а устное изложение и письменная запись ответа математически грамотны и отличаются последовательностью и аккуратностью.
Решение задачи считается безупречным, если правильно выбран способ решения, само решение сопровождается необходимыми объяснениями, верно выполнены нужные вычисления и преобразования, получен верный ответ, последовательно и аккуратно записано решение.
5. Оценка ответа учащегося при устном и письменном опросе проводится по пятибалльной системе, т.е. за ответ выставляется одна из отметок: 5 («отлично»), 4 («хорошо»), 3 («удовлетворительно»), 2 («неудовлетворительно»), 1 («плохо»).
Оценка устных ответов учащихся
Ответ оценивается отметкой «5», если ученик:
- полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;
- изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;
- правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
- показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;
- продемонстрировал усвоение ранее изученных сопутствующих вопросов, сформированность и устойчивость используемых при ответе умений и навыков;
- отвечал самостоятельно, без наводящих вопросов учителя;
- возможны одна-две неточности при освещении второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.
Ответ оценивается отметкой «4», если удовлетворяет в основном, требованиям на оценку «5», но при этом имеет один из недостатков:
- в изложении допущены небольшие пробелы, не исказившие математическое содержание ответа;
- допущены один-два недочетов при освещении основного содержании ответа, исправленные после замечания учителя;
- допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.
Отметка «3» ставится в следующих случаях:
- неполно раскрыто содержание материала (содержание изложено элементарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, недостаточные для дальнейшего усвоения программного материала (определенные «Требованиями к математической подготовки учащихся» в настоящей программе по математике);
- имелись затруднения или допущены ошибки в определении понятий, использовании математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
- ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
- при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.
Отметка «2» ставится в следующих случаях:
- не раскрыто основное содержание учебного материала;
- обнаружено незнание или непонимание учеником, большей или наиболее важной части учебного материала;
- допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.
Отметка «1» ставится если:
- ученик обнаружил полное незнание и непонимание изучаемого материала или не смог ответить ни на один из поставленных вопросов по изучаемому материалу.
Оценка письменных и контрольных работ учащихся
Отметка «5» ставится если:
- работа выполнена полностью;
- в логических рассуждениях и обосновании решения нет пробелов ошибок;
- в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнаний или непонимания учебного материала).
Отметка «4» ставится в следующих случаях:
- работа выполнена полностью, но обоснования шагов решения недостаточно (если умения обосновывать рассуждения не являлось специальным объектом проверки);
- допущена одна ошибка или есть две-три недочетов в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).
Отметка «3» ставится если:
- допущена более одной ошибки или более двух-трех недочетов в выкладках, чертежах или графиках, но учащийся обладает обязательными умениями по проверяемой теме.
Отметка «2» ставится если:
- допущена существенные ошибки, показавшие, что учащийся не обладает обязательными умениями по данной теме в полной мере.
Отметка «1» ставится если:
- работа показала полное отсутствие у учащегося обязательных знаний и умений по проверяемой теме или значительная часть работы выполнена не самостоятельно.
6. Учитель может повысить:
- отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии учащегося;
- за решение более сложной задачи или ответ на более сложный вопрос, предложенные учащемуся дополнительно после выполнения им каких-либо других заданий.
Общая классификация ошибок.
При оценке знаний, умений и навыков обучающихся следует учитывать все ошибки (грубые и негрубые) и недочёты.
Грубыми считаются ошибки:
-незнание определения основных понятий, законов, правил, основных положений теории, незнание формул, общепринятых символов обозначений величин, единиц их измерения;
-незнание наименований единиц измерения;
-неумение выделить в ответе главное;
-неумение применять знания, алгоритмы для решения задач;
-неумение делать выводы и обобщения;
-неумение читать и строить графики;
-неумение пользоваться первоисточниками, учебником и справочниками;
-потеря корня или сохранение постороннего корня;
-отбрасывание без объяснений одного из них;
-равнозначные им ошибки;
-вычислительные ошибки, если они не являются опиской;
-логические ошибки.
К негрубым ошибкам следует отнести:
-неточность формулировок, определений, понятий, теорий, вызванная неполнотой охвата основных признаков определяемого понятия или заменой одного - двух из этих признаков второстепенными;
-неточность графика;
-нерациональный метод решения задачи или недостаточно продуманный план ответа (нарушение логики, подмена отдельных основных вопросов второстепенными);
-нерациональные методы работы со справочной и другой литературой;
-неумение решать задачи, выполнять задания в общем виде.
Недочетами являются:
-нерациональные приемы вычислений и преобразований;
-небрежное выполнение записей, чертежей, схем, графиков.
УМК:
1 Учебник: Геометрия 7 – 9. Учебник для общеобразовательных учреждений. / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев, Э.Г.Позняк, И.И. Юдина. / М.: Просвещение, 2006 (и последующие издания) – 384 с.:ил.
2.Программа. Алгебра 7-9 Автор –составитель Зубарева И.И,Мордкович А.Г.- Москва , Мнемозина,2007.
3. Мордкович А.Г Алгебра. 7 класс, учебник, М.: Мнемозина,2009.
4.Мордкович А.Г Алгебра. 7 класс, задачник, М.: Мнемозина,2009.
Учебно-методическая литература:
1.Бурмистрова Т.А. Геометрия. 7 - 9 классы. Программы общеобразовательных учреждений. М., «Просвещение», 2009.
2.Дорофеев Г. В. и др. Оценка качества подготовки выпускников средней (полной) школы по математике. М., «Дрофа», 2002.
3.Концепция модернизации российского образования на период до 2010// «Вестник образования» -2002- № 6 - с.11-40.
4.Концепция математического образования (проект)//Математика в школе. - 2000. – № 2. – с.13-18.
5.Федеральный компонент государственного стандарта среднего (полного) общего образования по математике //«Вестник образования» -2004 - № 14 - с.107-119.

 Получите свидетельство
Получите свидетельство Вход
Вход











 Рабочая программа по математике 7 класс (0.52 MB)
Рабочая программа по математике 7 класс (0.52 MB)
 0
0 548
548 14
14 Нравится
0
Нравится
0


