Рабочая программа по математике (7 класс)

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА.

Рабочая программа учебного курса составлена на основе Примерной программы основного общего образования по математике в соответствии с федеральным компонентом государственного стандарта и с учетом рекомендаций авторских программ А. Г. Мордковича по алгебре и Л. С. Атанасяна по геометрии.

Согласно базисному учебному плану средней (полной) школы, рекомендациям Министерства образования Российской Федерации и наличию учебников в библиотеке, выбрана данная учебная программа и учебно - методический комплект.

Статус документа

Настоящая программа по математике (по алгебре и геометрии) для основной общеобразовательной школы 7 класса составлена на основе:

Федерального компонента государственного стандарта основного общего образования (приказ МОиН РФ от 05. 03. 2004г. № 1089);

Примерных программ по математике (письмо Департамента государственной политики в образовании Минобрнауки России от 07. 07. 2005г. № 03 - 1263);

«Временных требований к минимуму содержания основного общего образования» (приказ МО РФ от 19. 05. 98. № 1236);

Примерной программы общеобразовательных учреждений по геометрии 7–9 классы, к учебному комплексу для 7 - 9 классов (авторы Л. С. Атанасян, В. Ф. Бутузов, С. В. Кадомцев и др. , составитель Т. А. Бурмистрова – М: «Просвещение», 2008 г. );

Примерной программы общеобразовательных учреждений по алгебре 7–9 классы, к учебному комплексу для 7 - 9 классов (авторы А. Г. Мордкович, Л. А. Александрова, Т. Н. Мишустина, Е. Е. Тульчинская. – М. : Мнемозина, 2008 г. );

Программы: математика, 5 - 11 классы / авт. - сост. И. И. Зубарева, А. Г. Мордкович. – М. Мнемозина, 2007 г.

Цели изучения:

овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;

интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, пространственных представлений, способность к преодолению трудностей;

формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;

воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно - технического прогресса;

приобретение конкретных знаний о пространстве и практически значимых умений, формирование языка описания объектов окружающего мира, для развития пространственного воображения и интуиции, математической культуры, для эстетического воспитания обучающихся. Изучение геометрии вносит вклад в развитие логического мышления, в формирование понятия доказательства.

Тематическое планирование:

Весь материал - смотрите документ.

Календарно – тематическое планирование

РАБОЧАЯ ПРОГРАММА

муниципальное бюджетное общеобразовательное учреждение

«Средняя общеобразовательная школа №1» г. Мамадыш

Мамадышского муниципального района Республики Татарстан

Ризванова Лилия Галимзяновна — учитель математики

первой квалификационной категории

по математике для 7а, 7б классов

Рассмотрено на заседании педагогического совета

протокол № _____________

от «__» ___________ 2013 г.

2013-2014 учебный год

Рабочая программа математике для 7 класса по учебникам для общеобразовательных учреждений: «Алгебра 7» А.Г.Мордкович,

«Геометрия 7 – 9» Л.С.Атанасян, В.Ф.Бутузов, С.Б. Кадомцев и др.

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА.

Рабочая программа учебного курса составлена на основе Примерной программы основного общего образования по математике в соответствии с федеральным компонентом государственного стандарта и с учетом рекомендаций авторских программ А.Г. Мордковича по алгебре и Л.С. Атанасяна по геометрии.

Согласно базисному учебному плану средней (полной) школы, рекомендациям Министерства образования Российской Федерации и наличию учебников в библиотеке, выбрана данная учебная программа и учебно-методический комплект.

Статус документа

Настоящая программа по математике (по алгебре и геометрии) для основной общеобразовательной школы 7 класса составлена на основе:

• Федерального компонента государственного стандарта основного общего образования (приказ МОиН РФ от 05.03.2004г. № 1089);

• Примерных программ по математике (письмо Департамента государственной политики в образовании Минобрнауки России от 07.07.2005г. № 03-1263);

• «Временных требований к минимуму содержания основного общего образования» (приказ МО РФ от 19.05.98. № 1236);

• Примерной программы общеобразовательных учреждений по геометрии 7–9 классы, к учебному комплексу для 7-9 классов (авторы Л.С. Атанасян, В.Ф. Бутузов, С.В. Кадомцев и др., составитель Т.А. Бурмистрова – М: «Просвещение», 2008 г.);

• Примерной программы общеобразовательных учреждений по алгебре 7–9 классы, к учебному комплексу для 7-9 классов (авторы А.Г. Мордкович, Л.А. Александрова, Т.Н. Мишустина, Е.Е. Тульчинская. – М.: Мнемозина, 2008 г.);

• Программы: математика, 5-11 классы / авт.-сост. И.И. Зубарева, А.Г. Мордкович. – М. Мнемозина, 2007 г.

Цели изучения:

• овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;

• интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, пространственных представлений, способность к преодолению трудностей;

• формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;

• воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса;

• приобретение конкретных знаний о пространстве и практически значимых умений, формирование языка описания объектов окружающего мира, для развития пространственного воображения и интуиции, математической культуры, для эстетического воспитания обучающихся. Изучение геометрии вносит вклад в развитие логического мышления, в формирование понятия доказательства.

Общая характеристика учебного предмета

Математическое образование в основной школе складывается из следующих содержательных компонентов (точные названия блоков): арифметика; алгебра; геометрия; элементы комбинаторики, теории вероятностей, статистики и логики. В своей совокупности они отражают богатый опыт обучения математике в нашей стране, учитывают современные тенденции отечественной и зарубежной школы и позволяют реализовать поставленные перед школьным образованием цели на информационно емком и практически значимом материале. Эти содержательные компоненты, развиваясь на протяжении всех лет обучения, естественным образом переплетаются и взаимодействуют в учебных курсах.

Арифметика призвана способствовать приобретению практических навыков, необходимых для повседневной жизни. Она служит базой для всего дальнейшего изучения математики, способствует логическому развитию и формированию умения пользоваться алгоритмами.

Алгебра Изучение алгебры нацелено на формирование математического аппарата для решения задач из математики, смежных предметов, окружающей реальности. Язык алгебры подчеркивает значение математики как языка для построения математических моделей, процессов и явлений реального мира (одной из основных задач изучения алгебры является развитие алгоритмического мышле­ния, необходимого, в частности, для освоения курса информатики; овладение навыками дедуктивных рассуждений. Преобразование символических форм вносит свой специфический вклад в развитие воображения, способностей к математическому творчеству. Другой важной задачей изучения алгебры является получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов (равномерных, равноускоренных, экспоненциальных, периодических и др.), для формирования у обучающихся представлений о роли математики в развитии цивилизации и культуры.

Геометрия — один из важнейших компонентов математического образования, необходимый для приобретения конкретных знаний о пространстве и практически значимых умений, фор­мирования языка описания объектов окружающего мира, для развития пространственного воображения и интуиции, математи­ческой культуры, для эстетического воспитания обучающихся. Изучение геометрии вносит вклад в развитие логического мышления, в формирование понятия доказательства.

Элементы логики, комбинаторики, статистики и теории вероятностей становятся обязательным компонентом школьного образования, усиливающим его прикладное и практическое значение. Этот материал необходим, прежде всего, для формирования функциональной грамотности – умений воспринимать и анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей, производить простейшие вероятностные расчёты. Изучение основ комбинаторики позволит учащемуся осуществлять рассмотрение случаев, перебор и подсчёт числа вариантов, в том числе в простейших прикладных задачах. При изучении статистики и теории вероятностей обогащаются представления о современной картине мира и методах его исследования, формируется понимание роли статистики как источника социально значимой информации и закладываются основы вероятностного мышления.

Таким образом, в ходе освоения содержания курса учащиеся получают возможность:

• развить представление о числе и роли вычислений в человеческой практике; сформировать практические навыки выполнения устных, письменных, инструментальных вычислений, развить вычислительную культуру;

• овладеть символическим языком алгебры, выработать формально-оперативные алгебраические умения и научиться применять их к решению математических и нематематических задач;

• изучить свойства и графики элементарных функций, научиться использовать функционально-графические представления для описания и анализа реальных зависимостей;

• развить пространственные представления и изобразительные умения, освоить основные факты и методы планиметрии, познакомиться с простейшими пространственными телами и их свойствами;

• получить представления о статистических закономерностях в реальном мире и о различных способах их изучения, об особенностях выводов и прогнозов, носящих вероятностный характер;

• развить логическое мышление и речь – умения логически обосновывать суждения, проводить несложные систематизации, приводить примеры и контрпримеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства;

• сформировать представления об изучаемых понятиях и методах как важнейших средствах математического моделирования реальных процессов и явлений.

Требования к математической подготовке учащихся 7 класса

В результате изучения алгебры ученик должен

• знать/понимать

• существо понятия математического доказательства; примеры доказательств;

• существо понятия алгоритма; примеры алгоритмов;

• как используются математические формулы, уравнения; примеры их применения для решения математических и практических задач;

• как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;

• смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации;

• формулы сокращенного умножения;

• уметь

• составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;

• выполнять основные действия со степенями с натуральными показателями, с одночленами и многочленами; выполнять разложение многочленов на множители; сокращать алгебраические дроби;

• решать линейные уравнения и уравнения, сводящиеся к ним, системы двух линейных уравнений с двумя переменными;

• решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;

• определять координаты точки плоскости, строить точки с заданными координатами; строить графики линейных функций и функции y=x²;

• находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;

• определять свойства функции по ее графику; применять графические представления при решении уравнений и систем;

• описывать свойства изученных функций, строить их графики;

• использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

• выполнения расчетов по формулам, составления формул, выражающих зависимости между реальными величинами; нахождения нужной формулы в справочных материалах;

• моделирования практических ситуаций и исследования построенных моделей с использованием аппарата алгебры;

• описания зависимостей между физическими величинами соответствующими формулами при исследовании несложных практических ситуаций;

• интерпретации графиков реальных зависимостей между величинами.

В результате изучения геометрии ученик должен

• знать/понимать

• существо понятия математического доказательства; примеры доказательств;

• существо понятия алгоритма; примеры алгоритмов;

• как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;

• как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;

• как потребности практики привели математическую науку к необходимости расширения понятия числа;

• вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов;

• каким образом геометрия возникла из практических задач землемерия; примеры геометрических объектов и утверждений о них, важных для практики;

• смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации;

• уметь

• пользоваться языком геометрии для описания предметов окружающего мира;

• распознавать геометрические фигуры, различать их взаимное расположение;

• изображать геометрические фигуры; выполнять чертежи по условию задач; осуществлять преобразования фигур;

• вычислять значения геометрических величин (длин, углов, площадей, объемов), находить стороны, углы и площади треугольников, длины ломаных, дуг окружности, площадей основных геометрических фигур и фигур, составленных из них;

• решать геометрические задачи, опираясь на изученные свойства фигур и отношений между ними, применяя дополнительные построения, алгебраический аппарат, идеи симметрии;

• проводить доказательные рассуждения при решении задач, используя известные теоремы, обнаруживая возможности для их использования;

• использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

• описания реальных ситуаций на языке геометрии;

• расчетов, включающих простейшие формулы;

• решения практических задач, связанных с нахождением геометрических величин (используя при необходимости справочники и технические средства);

• построений геометрическими инструментами (линейка, угольник, циркуль, транспортир).

Изменение часов по некоторым темам основано на практическом опыте.

В соответствии с федеральным базисным учебным планом для образовательных учреждений Российской Федерации на изучение математики в 7 классе 5 часов в неделю. Исходя из расписания уроков и каникул календарно-тематическое планирование составлено на 175 уроков.

Контрольных работ – 11, из них 6 – по алгебре, 4 – по геометрии и одна итоговая.

Промежуточная аттестация проводится в форме тестов, самостоятельных, контрольных, проверочных работ и математических диктантов.

Уровень обучения – базовый.

Срок реализации рабочей учебной программы – один учебный год.

Учебно-методический комплекс учителя:

1. Геометрия, 7-9: Учеб. для общеобразоват. учреждений / Л.С. Атанасян, В.Ф. Бутузов, С.В. Кадомцев и др. — М.: Просвещение, 2008.

2. Изучение геометрии в 7, 8, 9 классах: Метод. рекомендации к учеб.: Кн. для учителя / Л.С. Атанасян, В.Ф. Бутузов, Ю.А. Глазков и др. — М.: Просвещение, 2003.

3. Задачи к урокам геометрии. 7-11 классы / Б.Г. Зив. — С.-Петербург, НПО «Мир и семья-95», 1998.

4. Геометрия: задачи на готовых чертежах: 7-9 классы / Э.Н. Балаян. — Ростов н/Д.: Феникс, 2009.

5. Геометрия: Учеб. для 7-11 кл. общеобразоват. учреждений / А.В. Погорелов. — М.: Просвещение, 1999.

6. Алгебра. 7 класс. В 2 ч. Ч. 1. Учебник для общеобразовательных учреждений / А.Г. Мордкович. — М.: Мнемозина, 2010.

7. Алгебра. 7 класс. В 2 ч. Ч. 2. Задачник для общеобразовательных учреждений / [А.Г. Мордкович и др.]; под ред. А.Г. Мордковича. — М.: Мнемозина, 2010.

Учебно-методический комплекс ученика:

1. Геометрия, 7-9: Учеб. для общеобразоват. учреждений / Л.С. Атанасян, В.Ф. Бутузов, С.В. Кадомцев и др. — М.: Просвещение, 2008.

2. Алгебра. 7 класс. В 2 ч. Ч. 1. Учебник для общеобразовательных учреждений / А.Г. Мордкович. — М.: Мнемозина, 2010.

3. Алгебра. 7 класс. В 2 ч. Ч. 2. Задачник для общеобразовательных учреждений / [А.Г. Мордкович и др.]; под ред. А.Г. Мордковича. — М.: Мнемозина, 2010.

Литература:

1. Алгебра, 7 класс. В 2 ч. Учебник и задачник для общеобразовательных учреждений / А.Г.Мордкович: Мнемозина, 2007.

2. Геометрия, 7 – 9. Учебник для общеобразовательных учреждений / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др.: Просвещение, 2005.

3. События. Вероятности. Статистическая обработка данных. Доп. Параграфы к курсу алгебры 7 – 9 классов общеобразовательных учреждений / А.Г. Мордкович, П.В.Семенов: Мнемозина, 2003.

4. Рабочая тетрадь по геометрии. / Т.М. Мищенко: ООО «Издательство АСТ», ООО «Издательство Астрель», 2008.

5. Алгебра. 7 – 9 кл. Методическое пособие для учителя А.Г. Мордкович:

Мнемозина, 2007.

1. Изучение геометрии в 7 – 9 классах. Методические рекомендации к учебнику. Книга для учителя / Л.С. Атанасян, В.Ф. Бутузов, Ю.А. Глазков: Просвещение, 2004.

2. Алгебра 7 класс. Контрольные работы для учащихся общеобразовательных учреждений / Л.А. Александрова: Мнемозина, 2009.

3. Алгебра 7 класс. Самостоятельные работы для учащихся общеобразовательных учреждений / Л.А. Александрова: Мнемозина, 2009.

4. Алгебра. Тесты для 7 – 9 кл. общеобразовательных учреждений / А.Г. Мордкович, Е.Е. Тульчинская: Мнемозина, 2004.

5. Дидактические материалы по геометрии для 7 класса / Б.Г. Зив, В.М. Мейлер: Просвещение 2004.

6. Самостоятельные и контрольные работы по алгебре и геометрии для 7 класса / А.П. Ершова, В.В. Голобородько, А.С. Ершов: Илекса, 2004.

7. Задачи и упражнения на готовых чертежах. 7 – 9 классы. Геометрия / Е.М. Рабинович: Илекса, 2001.

8. Задачи к урокам геометрии. 7-11 классы / Б.Г. Зив. — С.-Петербург, НПО «Мир и семья-95», 1998.

9. Геометрия: задачи на готовых чертежах: 7-9 классы / Э.Н. Балаян. — Ростов н/Д.: Феникс, 2009.

10. Газета «Математика» ИД «1 сентября», 2010.

11. http://www.alleng.ru

12. http://www.mathvaz.ru

1. Выполнить действия: а) (3а-4ах+2)-(11а-14ах); б) 3у² (у³+1).
2. Вынесите общий множитель за скобки: а) 10ав-15в²; б)18а³+6а².
3. Решите уравнение 9х-6(х-1)=5(х+2).
4. Пассажирский поезд за 4 часа прошел такое же расстояние, какое товарный за 6 ч. Найдите скорость пассажирского поезда, если известно, что скорость товарного на 20 км/ч меньше.
5. Упростите выражение: 2а(а+в-с)-2в(а-в-с)+2с(а-в+с)
6. Решите уравнение: 3х-1 _ х 5-х

1. Выполнить действия: а) (2а²-3а+1)-(7а²-5а); б) 3х (4у²-х).
2. Вынесите общий множитель за скобки: а) 2ху-3ху²; б)8в⁴+2в³.
3. Решите уравнение 7-4(3х-1)=5(1-2х).
4. В трех шестых классах 91 ученик. В 6А на 2 ученика меньше, чем в 6б, а в 6в на 3ученика больше, чем в 6б. Сколько учащихся в каждом классе?
5. Упростите выражение: 3х(х+у+с)-3у(х-у-с)-3с(х+у-с)
6. Решите уравнение: х-1 ₌ 5-х ₊ 3х

Итоговая контрольная работа за курс 7класса

1 вариант

1.Найдите значение выражения 50 – а³ при а = 4.

2.Решите линейное уравнение 8х – (2х +4) = 2(4х – 6).

3.Постройте графики линейных функций у = х +4 и у = 2х и найдите координаты их точки пересечения.

4.Упростите выражение (х + 6)² – 6(х – 3).

5.Разложите на множители двучлен с³ – 4с.

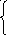
2х + у = 11,

6.Решите систему уравнений: 3х – 2у = 13.

---------------------------------------------------------------------------------------

7(Дополнительно). Два велосипедиста выехали из посёлка в город. Скорость первого велосипедиста была на 2 км/ч больше скорости второго. Первый велосипедист проехал путь за 4 ч, а второй 5 ч. Найдите скорость каждого велосипедиста.

Итоговая контрольная работа за курс 7класса

2 вариант

1.Найдите значение выражения 70 – а³ при а = 5.

2.Решите линейное уравнение 12х – (2х + 12) = 4(2х – 5).

3.Постройте графики линейных функций у = х +3 и у = -2х и найдите координаты их точки пересечения.

4.Упростите выражение (х + 4)² – 4(х – 3).

5.Разложите на множители двучлен 9с – с³.

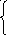
3х - 2у = 14,

6.Решите систему уравнений: 2х + у = 7.

---------------------------------------------------------------------------------------

7(Дополнительно). Два велосипедиста выехали из посёлка в город. Скорость первого велосипедиста была на 2 км/ч больше скорости второго. Первый велосипедист проехал путь за 4 ч, а второй 5 ч. Найдите скорость каждого велосипедиста.

Ответ оценивается отметкой «5», если:

• работа выполнена полностью;

• в логических рассуждениях и обосновании решения нет пробелов и ошибок;

в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания

• учебного материала).

Отметка «4» ставится в следующих случаях:

• работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);

• допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).

Отметка «3» ставится, если:

• допущено более одной ошибки или более двух – трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.

Отметка «2» ставится, если:

• допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.

Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.

Ответ оценивается отметкой «5», если ученик:

• полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;

• изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;

• правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;

• показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;

• продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков;

• отвечал самостоятельно, без наводящих вопросов учителя;

• возможны одна – две неточности при освещении второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.

Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:

• в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;

• допущены один – два недочета при освещении основного содержания ответа, исправленные после замечания учителя;

• допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.

Отметка «3» ставится в следующих случаях:

• неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала;

• имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;

• ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;

• при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.

Отметка «2» ставится в следующих случаях:

• не раскрыто основное содержание учебного материала;

• обнаружено незнание учеником большей или наиболее важной части учебного материала;

• допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.

Содержание рабочей программы.