Государственное бюджетное общеобразовательное учреждение
гимназия № 433
Курортного района Санкт - Петербурга
| Рассмотрено на заседании ШМО Протокол № _________ от «____»________201 г.
| Согласовано Зам. директора по УВР ______Л.Н.Филипченкова
| Утверждаю Приказ № _________ от «____»_______201 г. Директор ГБОУ гимназии № 433 _________Е.М.Волкова
|
РАБОЧАЯ ПРОГРАММА
по учебному курсу «Математика» в 5 классе
Базовый уровень
Классы: 5А, 5Б
Т.Н.Кащеева
учитель математики
2013/2014 учебный год
Пояснительная записка
Рабочая программа учебного курса математики для 5 класса составлена на основе Примерной программы основного общего образования по математике и программы курса математики для учащихся 5 классов общеобразовательных учреждений автора В.И.Жохова (2011 года).
Содержание программы направлено на освоение учащимися знаний, умений и навыков на базовом уровне, что соответствует Образовательной программе школы. Она включает все темы, предусмотренные федеральным компонентом государственного образовательного стандарта основного общего образования по математике. Программа рассчитана на 170 часов, по 5 часов в неделю.
Теоретический материал курса излагается на наглядно-интуитивном уровне, математические методы и законы формулируются в виде правил. Курс строится на индуктивной основе с привлечением дедуктивных рассуждений. Учебный процесс ориентирован на: рациональное сочетание устных и письменных видов работы как при изучении теории, так и при решении задач; сбалансированное сочетание традиционных и новых методов обучения; оптимизированное применение объяснительно-иллюстративных и эвристических методов; использование современных технических средств обучения.
Преобладающей формой текущего контроля выступает письменный (самостоятельные и контрольные работы) и устный опрос.
Для реализации учебной программы используется учебно-методический комплект, включающий:
Математика. 5 класс: учебник для общеобразовательных учреждений / Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. – М.: Мнемозина, 2010.
Жохов В.И. Преподавание математики в 5 – 6 классах: методическое пособие. – М.: Мнемозина, 2008.
Жохов В.И. Математика. 5 класс. Контрольные работы для учащихся общеобразовательных учреждений / В.И. Жохов, Л.Б. Крайнева. – М.: Мнемозина, 2010.
Жохов В.И. Математика. 5 класс. Диктанты для учащихся общеобразовательных учреждений / В.И. Жохов, И.М. Митяева. – М.: Мнемозина, 2010.
Жохов В.И. Математический тренажер. 5 класс: пособие для учителей и учащихся / В.И. Жохов. – М.: Мнемозина, 2010.
Цели программы обучения: систематическое развитие понятия числа; выработка умений выполнять устно и письменно арифметические действия над числами, переводить практические задачи на язык математики; подготовка учащихся к изучению систематических курсов алгебры и геометрии.
Задачи программы обучения:
– развитие навыка вычислений с натуральными числами;
– овладение навыками действий с обыкновенными и десятичными дробями;
– формирование начальных представлений об использовании букв для записи выражений и свойств арифметических действий, составлении уравнений;
– знакомство с геометрическими понятиями, приобретение навыков построения геометрических фигур и измерения геометрических величин;
– овладение конкретными математическими знаниями, необходимыми для применения в практической деятельности, для изучения смежных дисциплин;
– интеллектуальное развитие учащихся, формирование качеств мышления, характерных для математической деятельности;
– формирование представлений о математических идеях и методах;
– формирование преставлений о математике как части общечеловеческой культуры, понимания значимости математики для общественного прогресса.
Структура программы. Рабочая программа состоит из двух разделов: «Содержание обучения», «Требования к математической подготовке учащихся». К программе прилагаются: тематическое и поурочное планирование учебного материала; учебно-методические средства обучения.
Общая характеристика учебного предмета
Курс математики 5-го класса важное звено математического развития школьников. На этом этапе заканчивается в основном обучение счёту на множестве рациональных чисел, формируется понятие переменной и даются первые знания о приемах решения линейных уравнений, продолжается обучение решению текстовых задач, совершенствуются и обогащаются умения геометрических построений и измерений. Серьезное внимание уделяется формированию умений рассуждать, делать простые доказательства, давать обоснования выполняемых действий. При этом учащиеся постепенно осознают правила выполнения основных логических операций. Параллельно закладываются основы для изучения систематических курсов стереометрии, физики, химии и других смежных предметов.
Математическое образование в основной школе складывается из следующих содержательных компонентов (точные названия блоков): арифметика; алгебра; геометрия; элементы комбинаторики, статистики. В своей совокупности они отражают богатый опыт обучения математике в нашей стране, учитывают современные тенденции отечественной и зарубежной школы и позволяют реализовать поставленные перед школьным образованием цели на информационно емком и практически значимом материале. Эти содержательные компоненты, развиваясь на протяжении всех лет обучения, естественным образом переплетаются и взаимодействуют в учебных курсах.
Арифметика призвана способствовать приобретению практических навыков, необходимых для повседневной жизни. Она служит базой для всего дальнейшего изучения математики, способствует логическому развитию и формированию умения пользоваться алгоритмами.
Алгебра нацелена на формирование математического аппарата для решения задач из математики, смежных предметов, окружающей реальности. Язык алгебры подчеркивает значение математики как языка для построения математических моделей, процессов и явлений реального мира. Одной из основных задач изучения алгебры является развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики; овладение навыками дедуктивных рассуждений. Преобразование символических форм вносит свой специфический вклад в развитие воображения, способностей к математическому творчеству. Другой важной задачей изучения алгебры является получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов (равномерных, равноускоренных, экспоненциальных, периодических и др.), для формирования у учащихся представлений о роли математики в развитии цивилизации и культуры.
Геометрия – один из важнейших компонентов математического образования, необходимая для приобретения конкретных знаний о пространстве и практически значимых умений, формирования языка описания объектов окружающего мира, для развития пространственного воображения и интуиции, математической культуры, для эстетического воспитания учащихся. Изучение геометрии вносит вклад в развитие логического мышления, в формирование понятия доказательства.
Элементы комбинаторики и статистики становятся обязательным компонентом школьного образования, усиливающим его прикладное и практическое значение. Этот материал необходим, прежде всего, для формирования функциональной грамотности – умений воспринимать и анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей, производить простейшие вероятностные расчеты. Изучение основ комбинаторики позволит учащемуся осуществлять рассмотрение случаев, перебор и подсчет числа вариантов, в том числе в простейших прикладных задачах.
При изучении статистики и теории вероятностей обогащаются представления о современной картине мира и методах его исследования, формируется понимание роли статистики как источника социально значимой информации, и закладываются основы вероятностного мышления.
Таким образом, в ходе освоения содержания курса обучающиеся получают возможность:
развить представления о числе и роли вычислений в человеческой практике; сформировать практические навыки выполнения устных, письменных, инструментальных вычислений, развить вычислительную культуру;
овладеть символическим языком алгебры, выработать формально-оперативные алгебраические умения и научиться применять их к решению математических и нематематических задач;
изучить свойства и графики элементарных функций, научиться использовать функционально-графические представления для описания и анализа реальных зависимостей;
развить пространственные представления и изобразительные умения, освоить основные факты и методы планиметрии, познакомиться с простейшими пространственными телами и их свойствами;
получить представления о статистических закономерностях в реальном мире и о различных способах их изучения, об особенностях выводов и прогнозов, носящих вероятностный характер;
развить логическое мышление и речь – умения логически обосновывать суждения, проводить несложные систематизации, приводить примеры и контрпримеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства;
сформировать представления об изучаемых понятиях и методах как важнейших средствах математического моделирования реальных процессов и явлений.
Цели
Цели обучения математики в общеобразовательной школе определяются ее ролью в развитии общества в целом и формировании личности каждого отдельного человека.
В задачи обучения математики входит:
развитие внимания, мышления учащихся, формирования у них умений логически мыслить, анализировать полученные знания, находить закономерности;
овладение школьными знаниями о понятиях, правилах, законах, фактах;
развитие представлений о полной картине мира, о взаимосвязи математики с другими предметами.
Изучение математики на ступени основного общего образования направлено на достижение следующих целей:
овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, пространственных представлений, способность к преодолению трудностей;
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса.
Основные развивающие и воспитательные цели
Развитие: Ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей;
Математической речи;
Сенсорной сферы; двигательной моторики;
Внимания; памяти;
Навыков само и взаимопроверки.
Формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов.
Воспитание:
Культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса;
Волевых качеств;
Коммуникабельности;
Ответственности.
Целью изучения курса математики в 5 классе является систематическое развитие понятие числа, выработка умений выполнять устно и письменно арифметические действия над числами, переводить практические задачи на язык математики, подготовка учащихся к изучению систематических курсов алгебры и геометрии.
Промежуточная аттестация проводится в форме тестов, самостоятельных и проверочных работ, работ по индивидуальным карточкам, выполнения заданий у доски и математических диктантов (по 10-15 минут), контрольных работ в конце логически законченных блоков учебного материала. Итоговая аттестация предусмотрена в виде административной контрольной работы.
Место предмета в федеральном базисном учебном плане
Согласно федеральному базисному учебному плану в образовательном учреждении на изучение математики в 5 классе Программой отводится по 5 уроков в неделю, что составляет 175 часов в учебный год. Из них контрольных работ 14 часов, которые распределены по разделам следующим образом: «Натуральные числа и шкалы» 1 час, «Сложение и вычитание натуральных чисел» 2 часа, «Умножение и деление натуральных чисел» 2 часа, «Площади и объёмы» 1 час, «Обыкновенные дроби» 2 часа, «Сложение и вычитание десятичных дробей» 1 час, «Умножение и деление десятичных дробей» 2 часа, «Инструменты для вычислений и измерений» 2 часа и 1 час отведен на итоговую административную контрольную работу.
Данное планирование определяет достаточный объем учебного времени для повышения математических знаний учащихся в среднем звене школы, улучшения усвоения других учебных предметов.
Общеучебные умения, навыки и способы деятельности.
В ходе преподавания математики в основной школе, работы над формированием у обучающихся перечисленных в программе знаний и умений, следует обращать внимание на то, чтобы они овладевали умениями общеучебного характера, разнообразными способами деятельности, приобретали опыт:
планирования и осуществления алгоритмической деятельности, выполнения заданных и конструирования новых алгоритмов;
решения разнообразных классов задач из различных разделов курса, в том числе задач, требующих поиска пути и способов решения;
исследовательской деятельности, развития идей, проведения экспериментов, обобщения, постановки и формулирования новых задач;
ясного, точного, грамотного изложения своих мыслей в устной и письменной речи, использования различных языков математики (словесного, символического, графического), свободного перехода с одного языка на другой для иллюстрации, интерпретации, аргументации и доказательства;
проведения доказательных рассуждений, аргументации, выдвижения гипотез и их обоснования;
поиска, систематизации, анализа и классификации информации, использования разнообразных информационных источников, включая учебную и справочную литературу, современные информационные технологии.
Результаты обучения
Результаты обучения представлены в Требованиях к уровню подготовки и задают систему итоговых результатов обучения, которых должны достигать все учащиеся, оканчивающие основную школу, и достижение которых является обязательным условием положительной аттестации ученика за курс основной школы. Эти требования структурированы по трем компонентам: «знать/понимать», «уметь», «использовать приобретенные знания и умения в практической деятельности и повседневной жизни». При этом последние два компонента представлены отдельно по каждому из разделов содержания.
Требования к уровню подготовки учащихся
В результате изучения курса математики учащиеся должны:
Правильно употреблять термины, связанные с различными видами чисел и способами их записи: цельное, дробное, десятичная дробь, переход от одной формы записи к другой (например, проценты в виде десятичной дроби; выделение целой части из неправильной дроби); решать три основные задачи на дроби;
Сравнивать числа, упорядочивать наборы чисел, понимать связь отношений «больше», «меньше» с расположением точек на координатной прямой; находить среднее арифметическое нескольких чисел;
Выполнять арифметические действия с натуральными числами и десятичными дробями; округлять десятичные дроби;
Распознавать на чертежах и моделях геометрические фигуры (отрезки, углы, треугольники, многоугольники, окружность, круг); изображать указанные геометрические фигуры; владеть практическими навыками использования геометрических инструментов для построения и измерения отрезков и углов;
Владеть навыками вычисления по формулам, знать основные единицы измерения и уметь перейти от одних единиц измерения к другим в соответствии с условиями задачи;
Находить числовые значения буквенных выражений.
Требования к подготовке выпускников
В результате изучения математики ученик должен
знать/понимать
существо понятия математического доказательства; примеры доказательств;
существо понятия алгоритма; примеры алгоритмов;
как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;
как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;
как потребности практики привели математическую науку к необходимости расширения понятия числа;
вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов;
каким образом геометрия возникла из практических задач землемерия; примеры геометрических объектов и утверждений о них, важных для практики;
смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации.
Арифметика
уметь
выполнять устно арифметические действия: сложение и вычитание двузначных чисел и десятичных дробей; умножение однозначных чисел; арифметические операции с обыкновенными дробями с однозначным знаменателем и числителем;
переходить от одной формы записи чисел к другой, представлять десятичную дробь в виде обыкновенной и в простейших случаях обыкновенную в виде десятичной, проценты — в виде дроби и дробь — в виде процентов;
выполнять арифметические действия с рациональными числами, сравнивать рациональные и действительные числа; находить в несложных случаях значения степеней с целыми показателями; находить значения числовых выражений;
округлять целые числа и десятичные дроби;
пользоваться основными единицами длины, массы, времени, скорости, площади,; выражать более крупные единицы через более мелкие и наоборот;
решать текстовые задачи, задачи с дробями и процентами;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
решения несложных практических расчетных задач, в том числе c использованием при необходимости справочных материалов, калькулятора, компьютера;
устной прикидки и оценки результата вычислений; проверки результата вычисления с использованием различных приемов;
интерпретации результатов решения задач с учетом ограничений, связанных с реальными свойствами рассматриваемых процессов и явлений.
Алгебра
уметь
составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления;
решать простейшие линейные уравнения;
решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;
изображать числа точками на координатном луче;
определять координаты точки координатного луча, строить точки с заданными координатами;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
Геометрия
уметь
пользоваться геометрическим языком для описания предметов окружающего мира;
распознавать геометрические фигуры, различать их взаимное расположение;
изображать геометрические фигуры; выполнять чертежи по условию задач;
распознавать на чертежах, моделях и в окружающей обстановке основные пространственные тела, изображать их;
в простейших случаях строить развертки пространственных тел;
вычислять значения геометрических величин (длин, углов, площадей, объемов);
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
Элементы логики, комбинаторики, статистики
и теории вероятностей
извлекать информацию, представленную в таблицах, на диаграммах, графиках; составлять таблицы, строить диаграммы;
решать комбинаторные задачи путем систематического перебора возможных вариантов и с использованием правила умножения;
вычислять средние значения результатов измерений;
в простейших случаях строить развертки пространственных тел;
вычислять значения геометрических величин (длин, углов, площадей, объемов);
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
распознавания логически некорректных рассуждений;
анализа реальных числовых данных, представленных в виде диаграмм, графиков, таблиц;
решения практических задач в повседневной и профессиональной деятельности с использованием действий с числами, процентов, длин, площадей, объемов, времени, скорости;
решения учебных и практических задач, требующих систематического перебора вариантов.
Критерии оценивания знаний, умений и навыков обучающихся по математике.
(Согласно Методическому письму «Направления работы учителей математики
по исполнению единых требований преподавания предмета
на современном этапе развития школы»)
Для оценки достижений учащихся применяется пятибалльная система оценивания.
Нормы оценки:
1. Оценка письменных контрольных работ обучающихся по математике.
Ответ оценивается отметкой «5», если:
1) работа выполнена полностью;
2) в логических рассуждениях и обосновании решения нет пробелов и ошибок;
3) в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).
Отметка «4» ставится, если:
1) работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
2)допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).
Отметка «3» ставится, если:
1) допущено более одной ошибки или более двух – трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.
Отметка «2» ставится, если:
1) допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.
Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.
2.Оценка устных ответов обучающихся по математике
Ответ оценивается отметкой «5», если ученик:
полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;
изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;
правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;
продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков;
отвечал самостоятельно, без наводящих вопросов учителя;
возможны одна – две неточности при освещение второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.
Ответ оценивается отметкой «4»,
если удовлетворяет в основном требованиям на оценку «5»,
но при этом имеет один из недостатков:
в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;
допущены один – два недочета при освещении основного содержания ответа, исправленные после замечания учителя;
допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.
Отметка «3» ставится в следующих случаях:
неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала (определены «Требованиями к математической подготовке учащихся» в настоящей программе по математике);
имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.
Отметка «2» ставится в следующих случаях:
не раскрыто основное содержание учебного материала;
обнаружено незнание учеником большей или наиболее важной части учебного материала;
допущены ошибки в определении понятий, при использовании математической терминуологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.
Итоговая оценка знаний, умений и навыков
1. За учебную четверть и за год знания, умения и навыки учащихся по математике оцениваются одним баллом.
2. Основанием для выставления итоговой оценки знаний служат результаты наблюдений учителя за повседневной работой учеников, устного опроса, текущих и итоговых контрольных работ. Однако последним придается наибольшее значение.
3. При выставлении итоговой оценки учитывается как уровень теоретических знаний ученика, так и овладение им практическими умениями и навыками. Однако ученику не может быть выставлена положительная итоговая оценка по математике, если все или большинство его текущих обучающих и контрольных работ, а также итоговая контрольная работа оценены как неудовлетворительные, хотя его устные ответы оценивались положительно.
Промежуточная аттестация проводится в форме математических диктантов, тестов, самостоятельных работ, проверочных работ, взаимоконтроля.
Содержание учебного предмета
1. Натуральные числа и шкалы – 15 ч.
Обозначение натуральных чисел
Отрезок, Длина отрезка. Треугольник.
Плоскость, прямая, луч.
Шкалы и координаты.
Меньше или больше
Контрольная работа №1
Цель – систематизировать и обобщить сведения о натуральных числах, полученные в начальной школе; закрепить навыки построения и измерения отрезков.
Задачи – восстановить у учащихся навыки чтения и записи многозначных чисел, сравнения натуральных чисел, а также навыки измерения и построения отрезков. Ввести понятие координатного луча, единичного отрезка и координаты точки.
Понятия шкалы и делений, координатного луча
Знать и понимать:
Понятия натурального числа, цифры, десятичной записи числа, классов и разрядов.
Таблицу классов и разрядов. Обозначение разрядов.
Общепринятые сокращения в записи больших чисел, четные и нечетные числа, свойства натурального ряда чисел, однозначные, двузначные и многозначные числа.
Понятия отрезка и его концов, равных отрезков, середины отрезка, длины отрезка, значение отрезков.
Единицы измерения длины (массы) и соотношения между ними. Общепринятые сокращения в записи единиц длины (массы).
Измерительные инструменты.
Понятия треугольника, многоугольника, их вершин и сторон, их обозначение.
Понятия плоскости, прямой, луча, дополнительного луча, их обозначение.
Понятия шкалы и делений, координатного луча, единичного отрезка, координаты точки.
Понятия большего и меньшего натурального числа. Неравенство, знаки неравенств, двойное неравенство.
Уметь:
Читать и записывать натуральные числа, в том числе и многозначные.
Составлять числа из различных единиц.
Строить, обозначать и называть геометрические фигуры: отрезки, плоскости, прямые, находить координаты точек и строить точки по координатам.
Выражать длину (массу) в различных единицах.
Показывать предметы, дающие представление о плоскости.
Определять цену деления, проводить измерения с помощью приборов, строить шкалы с помощью выбранных единичных отрезков.
Чертить координатный луч, находить координаты точек и строить точки по координатам.
Сравнивать натуральные числа, в том числе и с помощью координатного луча.
Читать и записывать неравенства, двойные неравенства.
(Владеть способами познавательной деятельности).
2. Сложение и вычитание натуральных чисел – 21 ч.
| Сложение и вычитание натуральных чисел и его свойства. |
| Вычитание. |
| Контрольная работа №2 |
| Числовые и буквенные выражения |
| Буквенная запись свойств: сложения и вычитания |
| Уравнение. |
| Контрольная работа №3 |
Цель – закрепить и развить навыки сложения и вычитания натуральных чисел.
Задачи – уделить внимание закреплению алгоритмов арифметических действий над многозначными числами, т.к. они не только имеют самостоятельное значение, но и являются базой для формирования умений проводить вычисления с десятичными дробями. Составлять буквенные выражения по условию задач, решать уравнения на основе зависимости между компонентами действий (сложение и вычитание).
Знать:
Понятия действий сложения и
вычитания.
Компоненты сложения и вычитания.
Свойства сложения и вычитания натуральных чисел.
Понятие периметра многоугольника.
Алгоритм арифметических действий над многозначными числами.
Уметь:
Складывать и вычитать многозначные числа столбиком и при помощи координатного луча.
Находить неизвестные компоненты сложения и вычитания.
Использовать свойства сложения и вычитания для упрощения вычислений.
Решать текстовые задачи, используя действия сложения и вычитания.
Раскладывать число по разрядам и наоборот
3. Умножение и деление натуральных чисел – 26ч.
| Умножение натуральных чисел и его свойства |
| Деление |
| Деление с остатком |
| Контрольная работа №4 |
| Упрощение выражений |
| Порядок выполнения действий |
| Квадрат и куб числа |
| Контрольная работа №5 |
Цель – закрепить и развить навыки арифметических действий с натуральными числами.
Задачи – целенаправленное развитие и закрепление навыков умножения и деления многозначных чисел. Вводится понятие квадрата и куба числа. Продолжается работа по формированию навыков решения уравнений на основе зависимости между компонентами действий.
Знать и понимать:
Понятия программы вычислений и команды.
Таблицу умножения.
Понятия действий умножения и деления.
Компоненты умножения и деления.
Свойства умножения и деления натуральных чисел.
Порядок выполнения действий (в том числе, когда в выражении есть квадраты и кубы чисел).
Разложение числа на множители, приведение подобных слагаемых.
Деление с остатком, неполное частное, остаток.
Понятия квадрата и куба числа.
Таблицу квадратов и кубов первых десяти натуральных чисел
Уметь:
Заменять действие умножения сложением и наоборот.
Находить неизвестные компоненты умножения и деления.
Умножать и делить многозначные числа столбиком.
Выполнять деление с остатком.
Упрощать выражения с помощью вынесения общего множителя за скобки, приведения подобных членов выражения, используя свойства умножения.
Решать уравнения, которые сначала надо упростить.
Решать текстовые задачи арифметическим способом на отношения «больше (меньше) на … (в…); на известные зависимости между величинами (скоростью, временем и расстоянием; ценой, количеством и стоимостью товара и др.).
Решать текстовые задачи с помощью составления уравнения (в том числе задачи на части).
Изменять порядок действий для упрощения вычислений, осуществляя равносильные преобразования.
Составлять программу и схему программы вычислений на основании ее команд, находить значение выражений, используя программу вычислений.
Вычислять квадраты и кубы чисел.
Решать уравнения на основе зависимости между компонентами действий (умножение и деление).
4. Площади и объёмы – 12 ч.
| Формулы |
| Площадь. Формула площади прямоугольника, квадрата. |
| Единицы измерения площадей |
| Прямоугольный параллелепипед |
| Объемы. Объем прямоугольного параллелепипеда. |
| Контрольная работа №6 |
Цель – расширить представление учащихся об измерении геометрических величин на примере вычисления площадей и объемов, систематизировать известные им сведения об единице измерения.
Задачи – отработать навыки решения задач по формулам. Уделить внимание формированию знаний основных единиц измерения и умению перейти от одних единиц к другим в соответствии с условием задачи.
Знать и понимать: Понятие формулы.
Формулу пути (скорости, времени)
Понятия прямоугольника, квадрата, прямоугольного параллелепипеда, куба.
Измерения прямоугольного параллелепипеда.
Формулу площади прямоугольника, квадрата, треугольника.
Формулу объема прямоугольного параллелепипеда, куба.
Равные фигуры. Свойства
равных фигур.
Единицы измерения площадей и объемов.
Уметь:
Читать и записывать формулы.
Вычислять по формулам путь (скорость, время), периметр, площадь прямоугольника,
квадрата, треугольника, объем прямоугольного параллелепипеда, куба.
Вычислять площадь фигуры по количеству квадратных сантиметров, уложенных в ней.
Вычислять объем фигуры по количеству кубических сантиметров, уложенных в ней.
Решать задачи, используя свойства равных фигур.
5. Обыкновенные дроби – 19 ч.
| Окружность и круг |
| Доли. Обыкновенные дроби. |
| Сравнение дробей |
| Правильные и неправильные дроби |
| Контрольная работа №7 |
| Сложение и вычитание дробей с одинаковыми знаменателями |
| Деление и дроби |
| Смешанные числа |
| Сложение и вычитание смешанных чисел |
| Контрольная работа №8 |
Цель – познакомить учащихся с понятием дроби в объеме, достаточном для введения десятичных дробей.
Задачи – изучить сведения о дробных числах, необходимые для введения десятичных дробей. Уметь сравнивать дроби с одинаковыми знаменателями, выделять целые части дроби.
Знать и понимать:
Понятия окружности, круга и их элементов.
Понятия доли, обыкновенной дроби, числителя и знаменателя дроби.
Основные виды задач на дроби. Правило сравнения дробей.
Уметь:
Правила сложения и вычитания дробей с одинаковыми знаменателями.
Изображать окружность и круг с помощью циркуля, обозначать и называть их элементы.
Читать и записывать обыкновенные дроби.
Называть числитель и знаменатель дроби и объяснять, что ни показывают.
Изображать дроби, в том числе равные на координатном луче.
Распознавать и решать три основные задачи на дроби.
Сравнивать дроби с одинаковыми знаменателями.
Сравнивать правильные и неправильные дроби с единицей и друг с другом.
Записывать результат деления двух любых натуральных чисел с помощью обыкновенных
дробей.
Записывать любое натуральное число в виде обыкновенной дроби.
Выделять целую часть из неправильной дроби.
Представлять смешанное число в виде неправильной дроби.
6. Десятичные дроби. Сложение и вычитание десятичных дробей – 13ч.
| Десятичная запись дробных чисел |
| Сравнение десятичных дробей |
| Сложение и вычитание десятичных дробей |
| Приближенные значения чисел |
| Округление чисел |
| Контрольная работа №9 |
Цель – выработать умение читать, записывать, сравнивать, округлять десятичные дроби, выполнять сложение и вычитание десятичных дробей.
Задачи – четко представлять разряды рассматриваемого числа, уметь читать, записывать, сравнивать десятичные дроби.
Знать и понимать:
Понятие десятичной дроби, его целой и дробной части.
Правило сравнения десятичных дробей.
Правило сравнения десятичных дробей по разрядам.
Понятия равных, меньшей и большей десятичных дробей.
Правило сложения и вычитания десятичных дробей .
Свойства сложения и вычитания десятичных дробей.
Понятия приближенного значения числа, приближенного значения числа с недостатком
(с избытком).
Понятие округления числа.
Правило округления чисел,
десятичных дробей до заданных разрядов.
Уметь:
Иметь представление о десятичных разрядах.
Читать, записывать, сравнивать, округлять десятичные дроби.
Выражать данные значения длины, массы, площади, объема в виде десятичных дробей.
Изображать десятичные дроби
на координатном луче.
Складывать и вычитать десятичные дроби.
Раскладывать десятичные дроби по разрядам.
Решать текстовые задачи на сложение и вычитание, данные в которых выражены десятичными дробями.
Округлять десятичные дроби до заданного десятичного разряда.
7. Умножение и деление десятичных дробей – 26ч.
| Умножение десятичных дробей на натуральное число |
| Деление десятичных дробей на натуральное число |
| Контрольная работа №10 |
| Умножение десятичных дробей |
| Деление на десятичную дробь |
| Среднее арифметическое |
| Контрольная работа №11 |
Цель – выработать умение умножать и делить десятичные дроби, выполнять задания на все действия с натуральными числами и десятичными дробями.
Задачи – основное внимание привлекается к алгоритмической стороне рассматриваемых вопросов. На примерах отрабатывается правило постановки запятой в результате действия. Вводится понятие среднего арифметического нескольких чисел.
Знать и понимать:
Правило умножения двух десятичных дробей (правило постановки запятой в результате действия).
Правило деления числа на десятичную дробь (правило постановки запятой в результате действия).
Правило деления на 10, 100, 1000 и т.д.
Правило деления на 0,1; 0,01; 0,001;и т.д.
Свойства умножения и деления десятичных дробей.
Понятие среднего арифметического нескольких чисел.
Понятие средней скорости движения, средней урожайности, средней производительности.
Уметь:
Умножать и делить десятичную дробь на натуральное число, на десятичную дробь.
Выполнять задания на все действия с натуральными числами и десятичными дробями.
Применять свойства умножения и деления десятичных дробей при упрощении числовых и буквенных выражений и нахождении их значений.
Вычислять квадрат и куб заданной десятичной дроби.
Решать текстовые задачи на умножение и деление, а также на все действия, данные в которых выражены десятичными дробями.
Находить среднее арифметическое нескольких чисел.
Находить среднюю скорость движения, среднюю урожайность, среднюю производительность и т.д.
8. Инструменты для вычисления и измерения – 17ч.
| Микрокалькулятор |
| Проценты |
| Контрольная работа №12 |
| Угол. Прямой и развернутый углы. Чертежный треугольник. |
| Измерение углов. Транспортир |
| Круговые диаграммы |
| Контрольная работа №13 |
| Итоговое повторение 16 ч |
| Итоговая контрольная работа №14 |
| Анализ итоговой контрольной работы |
Цель – сформировать умения решать простейшие задачи на проценты, выполнять измерение и построение углов.
Задачи – понимать смысл термина «проценты». Учиться решать задачи на проценты; находить проценты от какой-либо величины; находить число, если известно несколько его процентов; находить, сколько процентов одно число составляет от другого. Формировать умения проводить измерения и строить углы. Учиться строить круговые диаграммы. Учить пользоваться калькулятором при вычислениях.
Знать и понимать:
Понятие процента. Знак, обозначающий «процент».
Правило перевода десятичной дроби в проценты и наоборот.
Основные виды задач на проценты.
Понятие угла и его элементов, обозначение углов, виды углов. Знак, обозначающий
«угол».
Свойство углов треугольника.
Измерительные инструменты.
Понятие биссектрисы угла.
Алгоритм построения круговых диаграмм.
Уметь:
Пользоваться калькуляторами при выполнении отдельных арифметических действий с натуральными числами и десятичными дробями.
Обращать десятичную дробь в проценты и наоборот.
Вычислять проценты с помощью калькулятора.
Распознавать и решать три вида задач на проценты: находить несколько процентов, от какой либо величины.
ТЕМАТИЧЕКСКОЕ (ПОУРОЧНОЕ) ПЛАНИРОВАНИЕ
| № п/п | Раздел, название урока в поурочном планировании | Дидактические единицы образовательного процесса | Контроль знаний учащихся | Коли- чество часов | Дата | Корректи- ровка |
|
| I четверть 45 |
|
| ГЛАВА I. Натуральные числа |
|
| 75 |
|
|
|
| §1. НАТУРАЛЬНЫЕ ЧИСЛА И ШКАЛЫ. | Основная цель: систематизировать и обобщить сведения о натуральных числах, полученные в начальной школе; закрепить навыки построения и измерения отрезков. | 15 |
|
|
| 1 2 3
| Обозначение натуральных чисел, п.1. | Знать и понимать: понятия натурального числа, цифры, десятичной записи числа, классов и разрядов; таблицу классов и разрядов, обозначение разрядов; общепринятые сокращения в записи больших чисел, четные и нечетные числа, свойства натурального ряда чисел, однозначные, двузначные и многозначные числа; понятия отрезка и его концов, равных отрезков, середины отрезка, длины отрезка, обозначение отрезков; единицы измерения длины (массы) и соотношения между ними; общепринятые сокращения в записи единиц длины (массы); измерительные инструменты; понятия треугольника, многоугольника, их вершин и сторон, их обозначение; понятия плоскости, прямой, луча, дополнительного луча, их обозначение; понятия шкалы и делений, координатного луча, единичного отрезка, координаты точки; понятия большего и меньшего натурального числа; неравенство, знаки неравенств, двойное неравенство. Уметь: читать и записывать натуральные числа, в том числе и многозначные; составлять числа из различных единиц; строить, обозначать и называть геометрические фигуры: отрезки, плоскости, прямые, находить координаты точек и строить точки по координатам; выражать длину (массу) в различных единицах; | Изучение и первичное закрепление новых знаний (беседа). СК Урок усвоения и закрепления новых умений. СК Урок обобщения и систематизации ЗУН. ВК | 3 |
|
|
| 4 5 6
| Отрезок, длина отрезка. Треугольник, п.2. | Урок совершенствования ЗУН. МД. ИК Комбинированный урок. Т-1. ИК. Урок самостоятельной практической работы. С-1. СК. ВК. ГК | 3 |
|
|
| 7 8 | Плоскость. Прямая. Луч.п.3. | Урок – практикум. СК. ГК Работа с моделями (частично-поисковая деятельность). Урок обобщения и систематизации ЗУН. ВК | 2 |
|
|
| 9 10 11 | Шкалы и координаты, п.4. | Урок усвоения нового материала. Практическая работа. ИК Комбинированные уроки. С-2. ИК | 3 |
|
|
| 12 13 14 | Меньше или больше, п.5. | определять цену деления, проводить измерения с помощью приборов, строить шкалы с помощью выбранных единичных отрезков; чертить координатный луч, находить координаты точек и строить точки по координатам; сравнивать натуральные числа, в том числе и с помощью координатного луча; читать и записывать неравенства, двойные неравенства; владеть способами познавательной деятельности. | Урок формирования новых умений. С-3. ИК. ГК Комбинированный урок. Т-2. ГК. ИК Урок комплексного применения ЗУН. ИК. ГК. СК | 3 |
|
|
| 15 | Контрольная работа №1 по теме «Натуральные числа и шкалы», п.1-5. | Уметь применять изученный теоретический материал при выполнении письменной работы. | Урок контроля, оценки знаний и умений. ТК.ФК | 1 |
|
|
|
| §2. СЛОЖЕНИЕ И ВЫЧИТАНИЕ НАТУРАЛЬНЫХ ЧИСЕЛ. | Основная цель: закрепить и развить навыки сложения и вычитания натуральных чисел. | 21 |
|
|
| 16 17 | Сложение натуральных чисел и его свойства, п.6. | Знать: понятия действий сложения и вычитания; компоненты сложения и вычитания; свойства сложения и вычитания натуральных чисел; понятие периметра многоугольника. алгоритм арифметических действий над многозначными числами. Уметь: находить неизвестные компоненты сложения и вычитания; использовать свойства сложения и вычитания для упрощения вычислений; решать текстовые задачи, используя действия сложения и вычитания; раскладывать число по разрядам и наоборот. | Усвоение изученного материала в процессе решения задач. Урок применения ЗУН. С-4. | 2 |
|
|
| 18 | Сложение натуральных чисел. (Разложение числа по разрядам), п.6. | Урок формирования умений и применения знаний. ГК. СК | 1 |
|
|
| 19 | Сложение натуральных чисел и его свойства. (Зависимость суммы от изменения компонентов), п.6. | Урок комплексного применения ЗУН. СК. ИК | 1 |
|
|
| 20 | Сложение натуральных чисел. Решение текстовых задач. (Периметр многоугольника), п.6. | Комбинированный. С-5. ИК | 1 |
|
|
| 21 | Вычитание натуральных чисел, п.7. | Комбинированный. Пр.р | 1 |
|
|
| 22 | Вычитание натуральных чисел. (Свойства вычитания), п.7. | Урок практических самост. работ. С-6. ИК | 1 |
|
|
| 23 | Вычитание натуральных чисел. Решение текстовых задач, п.7. | Урок комплексного применения ЗУН. С-7 | 1 |
|
|
| 24 | Сложение и вычитание натуральных чисел. Решение текстовых задач, п.6-7. | Закрепить в процессе решения задач, полученные ЗУН, подготовиться к контрольной работе. | Урок обобщения и систематизации знаний. ГК. СК | 1 |
|
|
| 25 | Контрольная работа №2 по теме «Сложение и вычитание натуральных чисел», пп.6-7. | Уметь применять теоретический материал при решении задач. | Урок контроля, оценки ЗУН. ТК. ФК | 1 |
|
|
| 26 | Числовое выражение, п.8. | Знать и понимать: понятия числового и буквенного выражений; буквенную запись свойств сложения и вычитания; понятия уравнения, его корня; понимать, что значит решить уравнение. Уметь: читать и записывать числовые выражения, находить значения выражений; читать и записывать буквенные выражения, выполнять подстановку числа вместо буквы; составлять числовые или буквенные выражения по условию задачи; составлять числовые и буквенные выражения для нахождения периметра многоугольника и находить его значение; упрощать буквенные выражения, используя свойства сложения и вычитания; находить длину отрезка по его частям и находить часть отрезка, зная величину всего отрезка и других его частей (записывать это с помощью числовых или букв.выражений); решать линейные уравнения на основе зависимости между компонентами действий (сложение и вычитание), выполнять проверку; решать текстовые задачи с помощью составления линейных уравнений. | Урок – игра. ГК. Т-3. ИК | 1 |
|
|
| 27 28 | Буквенное выражение и его числовое значение, п.8. | Урок беседа с необходимым минимумом задач. С-8. ГК. ИК Урок практикум. Обучающая сам.работа | 2 |
|
|
| 29 | Буквенное выражение. (Буквенная запись свойств сложения), п.9. | Урок приобретения новых знаний. С-9. ВК | 1 |
|
|
| 30 31 | Буквенное выражение. (Буквенная запись свойств сложения и вычитания), п.9. | Урок-практикум. Обучающая сам.раб. СК Урок-практикум. Т-4. | 2 |
|
|
| 32 33 | Уравнение, п.10. | Уроки усвоения новых знаний и умений в процессе решения уравнений. ГК. СК | 2 |
|
|
| 34 35 | Уравнение. (Решение текстовых задач с помощью составления уравнений), п.10. | Урок совершенствования знаний, умений и навыков. С-10. ИК Урок обобщения и систематизации знаний. | 2 |
|
|
| 36 | Контрольная работа №3 по теме «Числовые и буквенные выражения», пп.8-10. | Уметь применять изученный теоретический материал при выполнении письменной работы. | Урок контроля, оценки и коррекции знаний учащихся. ТК. ФК. | 1 |
|
|
|
| §3. УМНОЖЕНИЕ И ДЕЛЕНИЕ НАТУРАЛЬНЫХ ЧИСЕЛ. | Основная цель: закрепить и развить навыки арифметических действий с натуральными числами. | 27 |
|
|
| 37 38 | 39 Умножение натуральных чисел и его свойства, п.11. | Знать и понимать: порядок выполнения действий (в том числе, когда в выражении есть квадраты и кубы чисел); понятия программы вычислений и команды; таблицу умножения; понятия действий умножения и деления; компоненты умножения и деления; свойства умножения и деления натуральных чиселнаоборот. | Комбинированные уроки: лекция, практ.раб. | 2 |
|
|
| 39 40 41 | Умножение натуральных чисел. (Решение текстовых задач, уравнений), п.11. | Уроки: практикум; применения ЗУН , С-11;обобщения, С-12. ИК | 3 |
|
|
| 42 43 | Деление натуральных чисел. (Свойства деления), п.12. | Уроки-практикумы. Обучающая сам.раб. | 2 |
|
|
| 44 45 | Деление натуральных чисел, п. 12. (Решение текстовых задач, уравнен.). | Обучающий урок. СК. Игровой урок. СК. | 2 |
|
|
|
| II четверть35 |
| 46 47 48 | Деление натуральных чисел. Решение текстовых задач, (уравнений), п.12. | Уметь: заменять действие умножения сложением и находить неизвестные компоненты умножения и деления; умножать и делить многозначные числа столбиком; выполнять деление с остатком; | Усвоение изученного материала в процессе решения задач. С/Р обучающего характера с проверкой на уроке. СК. | 3 |
|
|
| 49 50 51 | Деление с остатком, п.13. | Усвоение нового материала в процессе решения задач. | 3 |
|
|
| 52 | Контрольная работа №4 по теме «Умножение и деление натуральных чисел», пп.11-13. | Уметь применять изученный теоретический материал при выполнении письменной работы. | Урок контроля, оценки и коррекции знаний учащихся. ФК. | 1 |
|
|
| 53 54 55 56 57 | Упрощение выражений, п.14. | Знать и понимать: порядок выполнения действий (в том числе, когда в выражении есть квадраты и кубы чисел); разложение числа на множители, приведение подобных слагаемых; деление с остатком, неполное частное, остаток; понятия квадрата и куба числа; таблицу квадратов и кубов первых десяти натуральных чисел. Уметь: упрощать выражения, используя свойства умножения; решать уравнения, которые сначала надо упростить; решать текстовые задачи арифметическим способом на отношения «больше (меньше) на … (в…); на известные зависимости между величинами (скоростью, временем и расстоянием и др.); решать текстовые задачи с помощью составления уравнения (в том числе задачи на части); изменять порядок действий для упрощения вычислений, осуществляя равносильные преобразования; составлять программу и схему программы вычислений на основании ее команд, находить значение выражений, используя программу вычислений; вычислять квадраты и кубы чисел. | Усвоение изученного материала в процессе решения задач. Проверочная С/Р. Индивидуальный контр. | 5 |
|
|
| 58 59 60 | Порядок выполнения действий, п.15. | Урок контроля, оценки и коррекции знаний учащихся. Тематический индивидуальный контроль. | 3 |
|
|
| 61 62 | Степень числа. Квадрат и куб числа, п.16. | Практический урок + объяснение. Проверочная работа Взаимоконтроль, индивидуальный контроль. | 2 |
|
|
| 63 | Контрольная работа №5 по теме «Упрощение выражений», пп.14-16. | Уметь применять изученный теоретический материал при выполнении письменной работы. | Урок контроля, оценки и коррекции знаний учащихся. ФК. | 1 |
|
|
|
| §4. ПЛОЩАДИ И ОБЪЕМЫ. | Основная цель: расширить представления учащихся об измерении геометрических величин на примере вычисления площадей и объемов и систематизировать известные им сведения о единицах измерения. | 12 |
|
|
| 64 65 | Формулы, п.17. | Знать и понимать: понятие формулы; формулу пути (скорости, времени); понятия прямоугольника, квадрата, прямоугольного параллелепипеда, куба; измерения прямоугольного параллелепипеда; формулу площади прямоугольника, квадрата, треугольника; формулу объема прямоугольного параллелепипеда, куба; равные фигуры; свойства равных фигур; единицы измерения площадей и объемов. Уметь: читать и записывать формулы; вычислять по формулам путь (скорость, время), периметр, площадь прямоугольника, квадрата, треугольника, объем прямоугольного параллелепипеда, куба; вычислять площадь фигуры по количеству квадратных сантиметров, уложенных в ней; вычислять объем фигуры по количеству кубических сантиметров, уложенных в ней; решать задачи, используя свойства равных фигур; переходить от одних единиц площадей (объемов) к другим. | Усвоение изученного материала в процессе решения задач. ВК. | 2 |
|
|
| 66 67 | Площадь. Формула площади прямоугольника, п.18. | Комбинированные уроки: лекция, практикум, проверочная СР. | 2 |
|
|
| 68 69 70 | Единицы измерения площадей, п.19. | Комбинированные уроки. ВК. ИК. МД. | 3 |
|
|
| 71 | Прямоугольный параллелепипед, п.20. | Практический урок + объяснение. Самостоятельная работа проверочная. ИК. | 1 |
|
|
| 72 73 74 | Объемы. Объем прямоугольного параллелепипеда, п.21. | Закрепление пройденного материала. Уроки практикумы. ВК. ИК. ГК. | 3 |
|
|
| 75 | Контрольная работа №6 по теме «Площади и объемы», пп.17-21. | Уметь применять изученный теоретический материал при выполнении письменной работы. | Урок контроля, оценки и коррекции знаний учащихся. ФК. | 1 |
|
|
|
| ГЛАВА II. Дробные числа. |
|
| 79 |
|
|
|
| §5. ОБЫКНОВЕННЫЕ ДРОБИ. | Основная цель: познакомить учащихся с понятием дроби в объеме, достаточном для введения десятичных дробей.
| 23 |
|
|
| 76 77 | Окружность и круг, п.22. | Знать и понимать: понятия окружности, круга и их элементов; понятия доли, обыкновенной дроби, числителя и знаменателя дроби; основные виды задач на дроби. Правило сравнения дробей. | Практическая работа, обучающая С/Р. | 2 |
|
|
| 78 79 80 | Доли, обыкновенные дроби, п.23. | Усвоение изученного материала в процессе решения задач. | 3 |
|
|
|
| III четверть50 |
| 81 | Основные задачи на дроби, п.23. | Уметь: правила сложения и вычитания дробей с одинаковыми знаменателями; изображать окружность и круг с помощью циркуля, обозначать и называть их элементы; читать и записывать обыкновенные дроби; называть числитель и знаменатель дроби и объяснять, что ни показывают; изображать дроби, в том числе равные на координатном луче; распознавать и решать три основные задачи на дроби; сравнивать дроби с одинаковыми знаменателями; сравнивать правильные и неправильные дроби с единицей и друг с другом; складывать и вычитать дроби с одинаковым знаменателем; записывать результат деления двух любых натуральных чисел с помощью обыкновенных дробей; записывать любое натуральное число в виде обыкновенной дроби; выделять целую часть из неправильной дроби; представлять смешанное число в виде неправильной дроби; складывать и вычитать смешанные числа. | Усвоение изученного материала в процессе решения задач. | 1 |
|
|
| 82 83 84 | Сравнение дробей, п.24. | Практический урок + объяснение. | 3 |
|
|
| 85 86 | Правильные и неправильные дроби, п.25. | Изучение нового материала. ВК. | 2 |
|
|
| 87 | Контрольная работа №7 по теме «Обыкновенные дроби», пп.22-25. | Урок с частично- поисковой деятельностью. СР. | 2 |
|
|
| 88 89 90
| Сложение и вычитание дробей с одинаковыми знаменателями, п.26.
| Урок обобщения и систематизации знаний. Практикум по решению задач. Групповой, устный и письменный контроль. | 3 |
|
|
| 91 92 | Деление и дроби, п.27. | Урок с частично- поисковой деятельностью. СР. | 2 |
|
|
| 93 94 | Смешанные числа, п.28. | Урок – игра. Групповой контроль. | 2 |
|
|
| 95 96 97 | Сложение и вычитание смешанных чисел, п.29.
| Закрепление пройденного материала. ИК. ВК. | 3 |
|
|
| 98 | Контрольная работа №8 по теме «Смешанные числа», пп.26-29. | Уметь применять изученный теоретический материал при выполнении письменной работы. | Урок контроля, оценки и коррекции знаний. ТК. | 1 |
|
|
|
| §6. ДЕСЯТИЧНЫЕ ДРОБИ. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДЕСЯТИЧНЫХ ДРОБЕЙ. | Основная цель: выработать умения читать, записывать, сравнивать, округлять десятичные дроби, выполнять сложение и вычитание десятичных дробей. | 13 |
|
|
| 99 100 | Десятичная запись дробных чисел, п.30. | Знать и понимать: понятие десятичной дроби, его целой и дробной части; правило сравнения десятичных дробей. правило сравнения десятичных дробей по разрядам; понятия равных, меньшей и большей десятичных дробей; правило сложения и вычитания десятичных дробей (правило постановки запятой в результате действия); свойства сложения и вычитания десятичных дробей; понятия приближенного значения числа с недостатком (с избытком); понятие округления числа; правило округления десятичных дробей до заданных разрядов. Уметь: иметь представление о десятичных разрядах; читать, записывать, сравнивать, округлять десятичные дроби; выражать данные значения длины, массы, площади, объема в виде десятичных дробей; изображать десятичные дроби на координатном луче; складывать и вычитать десятичные дроби; раскладывать десятичные дроби по разрядам; решать текстовые задачи на сложение и вычитание, данные в которых выражены десятичными дробями; округлять десятичные дроби до заданного десятичного разряда. | Усвоение изученного материала в процессе решения задач. МД. | 2 |
|
|
| 101 102 103 | Сравнение десятичных дробей, п.31. | Обучающий, тест. Усвоение изученного материала в процессе решения задач. ВК. ИК. | 3 |
|
|
| 104 105 106 107 108 | Сложение и вычитание десятичных дробей, п.32. | Игровой урок. Работа в группах. Закрепление пройденного материала в процессе решения задач. ГК. ВК.ИК. СР. | 5 |
|
|
| 109 110 | Приближенные значения чисел. Округление чисел, п.33. | Усвоение изученного материала в процессе решения задач. ИК. СР. | 2 |
|
|
| 111 | Контрольная работа №9 по теме «Сложение и вычитание десятичных дробей», пп.30-33. | Урок контроля, оценки и коррекции знаний учащихся. Фронтальный контроль. | 1 |
|
|
|
| §7. УМНОЖЕНИЕ И ДЕЛЕНИЕ ДЕСЯТИЧНЫХ ДРОБЕЙ. | Основная цель: выработать умение умножать и делить десятичные дроби, выполнять задания на все действия с натуральными числами и десятичными дробями. | 26 |
|
|
| 112 | Умножение десятичных дробей на натуральные числа, п.34. | Знать и понимать: правило умножения двух десятичных дробей (правило постановки запятой в результате действия); правило деления числа на десятичную дробь (правило постановки запятой в результате действия); правило деления на 10, 100, 1000 и т.д;
| Усвоение изученного материала. | 1 |
|
|
| 113 | Умножение десятичных дробей на натуральные числа (упрощение выражений), п.34. | Практикум по решению задач. ВК. ИК.
|
|
|
|
| 114 | Умножение десятичных дробей на натуральные числа. (Решение текстовых задач, уравнений), п.34. | Игровой урок. Работа в группах. | 1 |
|
|
| 115 | Деление десятичных дробей на натуральные числа, п.35. | правило деления на 0,1; 0,01; 0,001 и т.д; свойства умножения и деления десятичных дробей; понятие среднего арифметического нескольких чисел; понятие средней скорости движения, средней урожайности, средней производительности.
Уметь: умножать и делить десятичную дробь на натуральное число, на десятичную дробь; выполнять задания на все действия с натуральными числами и десятичными дробями; применять свойства умножения и деления десятичных дробей при упрощении числовых и буквенных выражений и нахождении их значений; вычислять квадрат и куб заданной десятичной дроби; решать текстовые задачи на умножение и деление, а также на все действия, данные в которых выражены десятичными дробями; находить среднее арифметическое нескольких чисел; находить среднюю скорость движения, среднюю урожайность, среднюю производительность и т.д.; | Усвоение изученного материала. ВК. | 1 |
|
|
| 116 | Деление десятичных дробей на натуральные числа (упрощение числовых и буквенных выражений). | Усвоение изученного материала в процессе решения задач. СР | 1 |
|
|
| 117 118 | Деление десятичных дробей на натуральные числа. (Решение текстовых задач, уравнений), п.35. | Урок с частично- поисковой деятельностью. СР. | 2 |
|
|
| 119 | Умножение и деление десятичных дробей на натуральные числа, пп.34-35. | Игровой урок. Работа в группах. Закрепление пройденного материала | 1 |
|
|
| 120 | Контрольная работа №10 по теме «Умножение и деление десятичной дроби на натуральное число», пп.34-35. | Урок контроля, оценки и коррекции знаний учащихся. Фронтальный контроль. | 1 |
|
|
| 121 122 123 124 125 | Умножение десятичных дробей, п.36. | Изучение нового материала. Усвоение изученного материала в процессе решения задач. СР. ИК. | 5 |
|
|
| 126 127 128 129 | Деление на десятичную дробь, п.37. | Усвоение изученного материала в процессе решения задач. СР. | 4 |
|
|
| 130 | Итоговое занятие III четверти. | Урок обобщения и систематизации знаний. ТК. | 1 |
|
|
|
| VI четверть 40 |
| 131 132 | Деление на десятичную дробь, п.37. | находить среднее арифметическое нескольких чисел; находить среднюю скорость движения, среднюю урожайность, среднюю производительность и т.д. | Комбинированные уроки. ГК | 2 |
|
|
| 133 134 135 136 | Среднее арифметическое, п.38. | Комбинированные уроки. ИК | 4 |
|
|
| 137 | Контрольная работа №11 по теме «Умножение и деление десятичных дробей», пп.36-38. | Уметь применять изученный теоретический материал при выполнении письменной работы. | Урок контроля, оценки и коррекции знаний учащихся. ФК. | 1 |
|
|
|
| §8. ИНСТРУМЕНТЫ ДЛЯ ВЫЧИСЛЕНИЙ И ИЗМЕРЕНИЙ. | Основная цель: сформировать умения решать простейшие задачи на проценты, выполнять измерение и построение углов. | 17 |
|
|
| 138 139 | Микрокалькулятор, п.39 (начальные сведения о вычислениях на калькуляторе). | Знать и понимать: понятие процента. Знак, обозначающий «процент»; правило перевода десятичной дроби в проценты и наоборот; основные виды задач на проценты; понятие угла и его элементов, обозначение углов, виды углов; знак, обозначающий «угол»; свойство углов треугольника; измерительные инструменты; понятие биссектрисы угла;. алгоритм построения круговых диаграмм. Уметь: обращать десятичную дробь в проценты и наоборот; вычислять проценты с помощью калькулятора. распознавать и решать три вида задач на проценты: находить несколько процентов, от какой либо величины. | Урок усвоения новых знаний, умений и навыков. | 2 |
|
|
| 140 141 | Проценты, п.40. | Комбинированный урок | 2 |
|
|
| 142 143 144 | Основные задачи на проценты, п.40. | Урок учебный практикум | 3 |
|
|
| 145 | Контрольная работа №12 по теме «Проценты», пп.39-40. | Урок контроля, оценки и коррекции знаний учащихся. ФК. | 1 |
|
|
| 146 147 148 | Угол. Прямой и развернутый угол. Чертежный треугольник, п.41. | Урок усвоения новых знаний, умений и навыков. | 3 |
|
|
| 149 150 151 | Измерение углов. Транспортир, п.42. | Обучающий урок. Урок практикум. СР обучающая. | 3 |
|
|
| 152 153 | Круговые диаграммы, п.43. | Беседа. Выполнение творческого задания. ИК. | 2 |
|
|
| 154 | Контрольная работа №13 по теме «Угол. Транспортир», пп.41-43. | Уметь применять изученный теоретический материал при выполнении письменной работы. | Урок контроля, оценки и коррекции знаний учащихся. ФК. | 1 |
|
|
|
| Итоговое повторение |
|
| 16 |
|
|
| 155 156 | Натуральные числа. | Знать и понимать: основные математические понятия, термины, формулы, свойства, способы решения уравнений и задач, преобразования выражений, изучаемых в курсе математики 5 класса. Уметь: выполнять простейшие устные вычисления; читать и записывать натуральные числа и десятичные дроби, сравнивать два числа; выполнять письменно сложение, вычитание, умножение и деление натуральных чисел и десятичных дробей; | Урок «занимательных задач» | 2 |
|
|
| 157 158 | Площади и объемы. | Решение задач. СР обучающая. ИК. | 2 |
|
|
| 159 160 161 | Обыкновенные дроби. | Обучающий урок. Урок практикум. Самостоятельная работа обучающая. | 3 |
|
|
| 162 163 164 | Десятичные дроби. | Урок обобщения и систематизации знаний. Уроки – практикумы. | 3 |
|
|
| 165 166 | Проценты. | определять порядок действий и находить значения числовых выражений; решать текстовые задачи арифметическим способом; распознавать на рисунках и моделях геометрические фигуры (линии, прямоугольный параллелепипед, куб), соотносить геометрические формы с формой окружающих предметов; владеть практическими геометрическими навыками. | Уроки – практикумы. | 2 |
|
|
| 167 168 | Углы. | Уроки обобщения и систематизации знаний. | 2 |
|
|
| 169 | Контрольная работа №14 «Итоговая контрольная работа за курс математики 5-го класса». | Урок контроля, оценки и коррекции знаний учащихся. ФК. | 1 |
|
|
| 170 | Итоговое занятие. | Урок обобщения и систематизации знаний. | 1 |
|
|
УЧЕБНО-МЕТОДИЧЕСКИЕ СРЕДСТВА ОБУЧЕНИЯ
Депман И.Я. За страницами учебника математики: книга для чтения учащимися 5 – 6 классов / И.Я. Депман, Н.Я. Виленкин. – М.: Просвещение, 1999. – 288 с.
Ерина Т.М.. Рабочая тетрадь по математике. 5 класс. – М.: Экзамен, 2011. – 128 с.
Жохов В.И. Программа. Планирование учебного материала. Математика. 5-6 классы. – М.: Мнемозина, 2011. – 32 с.
Жохов В.И. Преподавание математики в 5 – 6 классах: методическое пособие. – М.: Мнемозина, 2008. – 239 с.
Жохов В.И. Математика. 5 класс. Контрольные работы для учащихся общеобразовательных учреждений / В.И. Жохов, Л.Б. Крайнева. – М.: Мнемозина, 2010. – 64 с.
Жохов В.И. Математика. 5 класс. Диктанты для учащихся общеобразовательных учреждений / В.И. Жохов, И.М. Митяева. – М.: Мнемозина, 2010. – 96 с.
Жохов В.И. Математический тренажер. 5 класс: пособие для учителей и учащихся / В.И. Жохов. – М.: Мнемозина, 2010. – 48 с.
Кузнецова Г.М. Программы для общеобразовательных школ, гимназий, лицеев. Математика, 5 – 11 кл. / Г.М. Кузнецова, Н.Г. Миндюк. – 4-е изд., стереотип. М.: Дрофа, 2004. – 320с.
Лысенко Ф.Ф. Тесты для промежуточной аттестации. Математика, 5-6 класс / Ф.Ф. Лысенко, Л.С. Ольхова, С.Ю. Кулабухов. – Ростов-на-Дону: Легион, 2010. – 157 с.
Математика. 5 класс: учебник для общеобразовательных учреждений / Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. – М.: Мнемозина, 2010. – 288 с.
Попова Л.П. Контрольно-измерительные материалы. 5 класс. – М.: ВАКО, 2010. – 93 с.
Рудницкая В.Н. Рабочая тетрадь по математике №1. 5 класс. – М.: Мнемозина, 2010.
Рудницкая В.Н. Рабочая тетрадь по математике №2. 5 класс. – М.: Мнемозина, 2010.
Учебное интерактивное пособие к учебнику Н.Я. Виленкина, В.И. Жохова, А.С. Чеснокова, С.И. Шварцбурда «Математика» 5 кл. – М.: Мнемозина, 2009. – (CD-ROM)
Чесноков А.С. Дидактические материалы по математике для 5 класса / А.С. Чесноков, К.И. Нешков. – М: Классикс Стиль, 2009. – 165 с.
Контрольные работы
Контрольная работа №1
Вариант I
№1 Найдите сумму:
а) 3000000+5000+7
б) 654+765
№2 Выполнить действия:
(60+40):2 – 30:5
№3 Сравните числа и поставьте вместо звездочки знак
а) 63001 * 63002
б) 41527 * 42326
№4 Задача. От туристского лагеря до города 84 км. Турист ехал на велосипеде из лагеря в город со скоростью 12 км/ч., а возвращался по той же дороге со скоростью 14 км/ч. На какой путь турист затратил больше времени и на сколько часов.
Вариант II
№1 Найдите сумму:
а) 2000000+7000+300+2
б) 763+448
№2 Выполнить действия:
(70-50)∙5:20+55
№3 Сравните числа и поставьте вместо звездочки знак
а) 20850 * 20860
б) 31255 * 32254
№4 Задача. Игорь живет на расстоянии48 км от районного центра. Путь от дома до райцентра он проехал на велосипеде со скоростью 16 км/ч, а обратный путь по той же дороге он проехал со скоростью 12 км/ч. На какой путь Игорь затратил меньше времени и насколько часов.
Контрольная работа №2
Вариант I
№1 Выполнить действия:
а) (829-239)*75
б) 8991:111:3
№2 Задача. Периметр треугольника 36 см, а периметр прямоугольника в 3 раза меньше. На сколько сантиметров периметр треугольника больше периметра прямоугольника?
№3 Вычислить:
4кг – 80гр
№4
а) На сколько число 59345 больше числа 53568?
б) На сколько число 59345 меньше числа 69965?
№5 Задача. Вдоль аллеи (по прямой) высадили 15 кустов. Расстояние между любыми двумя соседними кустами одинаковое. Найдите это расстояние, если между крайними кустами 210дм.
Вариант II
№1 Выполнить действия:
а) 2000 – (859+1085):243
б) 3969:(305 – 158)
№2 Задача. Туристы в первый день ехали на велосипедах 6 часов со скоростью 12 км/ч, во - второй день они проехали с одинаковой скоростью такой же путь за 4 часа. С какой же скоростью ехали туристы во – второй день?
№3 Вычислить:
2кг – 60гр
№4
а) на сколько число 38954 больше числа 22359
б) На сколько число 38954 меньше числа 48234.
№5 Задача. Вдоль шоссе (по прямой) высадили 20 деревьев. Расстояние между любыми двумя соседними деревьями одинаковое. Найдите это расстояние, если между крайними деревьями 380м.
Контрольная работа №3
Вариант I
№1 Решите уравнение: а) 21+х=56
б) у-89=90
№2 Найти значение выражения: 260+в – 160, если в=93
№3 Вычислите, выбирая удобный порядок действий
а) 5+1977+1515
б) 863 – (163+387)
№4 Решить задачу с помощью уравнения.
В автобусе было 78 пассажиров. После того, как на остановке из него несколько человек вышли, в автобусе осталось 59 пассажиров. Сколько человек вышли из автобуса на остановке.
№5
На отрезке MN =19, отметили точку К такую, что МК=15 и точку F такую, что FN=13. Найти длину отрезка KF.
Вариант II
№1 Решите уравнение: а) х+32=68
б) 76 – у=24
№2 Найти значение выражения: 340+к – 240, если к=87
№3 Вычислите, выбирая удобный порядок действий
а) 7231+1437+563
б) (964+479) – 264
№4 Решить задачу с помощью уравнения.
В санатории было 97 отдыхающих. После того, как несколько человек уехали на экскурсию, в санатории осталось 78 отдыхающих. Сколько отдыхающих уехали на экскурсию.
№5
На отрезке DE=25 отметили точку L такую, что DL=19, и точку Р такую, что РЕ=17. Найдите длину отрезка LP.
Контрольная работа №4
Вариант I
№1 Найдите значение выражения: а) 58∙196 б) 405∙208 в) 36490:178
№2 Решите уравнение
а) х∙14=112 б) 133:у=19 в) m:15=90
№3 Вычислите, выбирая удобный порядок действий.
а) 4∙289∙25
б) 50∙97∙20
№4 Задача. Коля задумал число, умножил его на 3 и от произведения отнял 7. Он получил 50. Какое число задумал Коля?
№5 Угадайте корень уравнения и сделайте проверку:
х+х – 20=х+5
Вариант II
№1 Найдите значение выражения:
а) 67∙189 б) 306∙805 в) 38130:186
№2 Решите уравнение
а) х∙13=182 б) 187:у=17 в) n:14=98
№3 Вычислите, выбирая удобный порядок действий.
а) 25∙197∙4
б) 50∙23∙40
№4 Задача. Света задумала число, умножила его на 4 и к произведению прибавила 8. Получила 60. Какое число задумала Света?
№5 Угадайте корень уравнения и сделайте проверку:
у+у – 25=у+10
Контрольная работа №5
Вариант I
№1 Найдите значение выражения:
а) 684∙397 - 584∙397
б) 39∙58 – 9720:27+33
в) 23 + 32
№2 Решите уравнение:
а) 7у – 39=717 б) х+3х=76
№3 Упростите выражение:
а) 24а+16+13а б) 25∙m∙16
№4 Задача. В книге напечатаны 2 сказки. Первая занимает в 4 раза больше страниц, чем вторая, а обе они занимают 30 стр. Сколько страниц занимает каждая сказка?
№5 Имеет ли корни уравнение:
х2=х:х
Вариант II
№1 Найдите значение выражения:
а) 798∙349-798∙249
б) 57∙38-8640:24+66
в) 52+33
№2 Решите уравнение:
а) 8х+14=870 б) 5у-у=68
№3 Упростите выражение:
а) 37к+13+22к б) 50∙n∙12
№4 Задача. В двух корзинах 98 яблок. В первой яблок в шесть раз меньше, чем во второй. Сколько яблок в каждой корзине?
№5 Имеет ли корни уравнение:
у3=у∙у
Контрольная работа №6
Вариант I
1. Вычислите:
а) (53+132):21
б) 180∙94-47700:45+4946
2. Задача. Длина прямоугольного участка земли 125м, а ширина 96м. Найдите площадь поля и выразите её в арах.
3. Задача. Найдите объем прямоугольного параллелепипеда, измерения которого равны 4м, 3м и 5 дм.
4. Используя формулу пути s=v∙t, найдите:
а) путь, пройденный автомашиной за 3 ч, если её скорость 80 км/ч,
б) время движения катера, прошедшего 90 км со скоростью 15 км/ч
5. Задача. Найдите площадь поверхности и объем куба, ребро которого равно 6 дм. Во сколько раз уменьшится площадь поверхности и во сколько раз – объем куба, если ребро уменьшить вдвое?
Вариант II
1. Вычислите:
а) (63+122):15
б) 86∙170-5793+72800:35
2. Задача. Ширина прямоугольного поля 375м, а длина 1600м. Найдите площадь поля и выразите её в гектарах.
3. Задача. Найдите объем прямоугольного параллелепипеда, измерения которого равны 2дм, 6дм и 5 см.
4. Используя формулу пути s=v∙t, найдите:
а) путь, пройденный моторной лодкой за 2 часа, если её скорость 18 км/ч
б) скорость движения автомобиля, за 3 ч прошедшего 150 км.
5. Задача. Ребро куба равно 5см. Найдите площадь поверхности и объем этого куба. Во сколько раз увеличится площадь поверхности и во сколько раз – объем куба, если его ребро увеличить вдвое?
Контрольная работа №7
Вариант I
1. Примите за единичный отрезок длину 8 клеток тетради и отметьте на координатном луче точки А(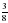 ), М(
), М(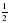 ), К(
), К(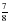 ), Т(
), Т(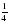 ), Р(
), Р(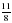 )
)
2. Сравните числа: а) 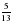 и
и 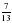 , б)
, б) 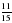 и
и 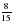 , в) 1 и
, в) 1 и 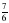 , г)
, г) 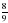 и
и 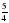
3. Сложите 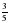 числа 30 и
числа 30 и 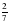 числа 14.
числа 14.
4. Какую часть составляют:
а) 9 см2 от квадратного дециметра,
б) 17 дм3 от кубического метра,
в) 13 кг от 2 ц?
5. Задача. Ширина прямоугольника 48 см, что составляет 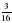 его периметра. Найдите длину этого прямоугольника.
его периметра. Найдите длину этого прямоугольника.
Вариант II
1. Примите за единичный отрезок длину 12 клеток тетради и отметьте на координатном луче точки В(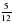 ), С(
), С(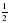 ), Е(
), Е(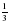 ), О(
), О(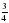 ), Н(
), Н(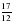 )
)
2. Сравните числа: а) 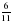 и
и 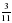 , б)
, б)  и
и 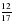 , в) 1 и
, в) 1 и 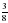 , г)
, г)  и
и 
3. Сложите  числа 18 и
числа 18 и  числа 40.
числа 40.
4. Какую часть составляют:
а) 7 дм2 от квадратного метра,
б) 19 см3 от кубического дециметра,
в) 9ц от 4 т?
5. Задача. Длина прямоугольника составляет  его периметра. Найдите ширину этого прямоугольника, если его длина равна 80 см.
его периметра. Найдите ширину этого прямоугольника, если его длина равна 80 см.
Контрольная работа №8
Вариант I
1. Выполните действия:
а)  б)
б) 
в)  г)
г) 
2. Задача. Турист шел с постоянной скоростью и за 3 часа прошел 14 км. С какой скоростью он шел?
3. Задача. В гараже 45 автомобилей. Из них  - легковые. Сколько легковых автомобилей в гараже.
- легковые. Сколько легковых автомобилей в гараже.
4. Решите уравнение:
а)  б)
б) 
5. Какое число надо разделить на 8, чтобы частное равнялось  ?
?
Вариант II
1. Выполните действия:
а)  б)
б) 
в) г)
г) 
2. Задача. Автомобиль, двигаясь с постоянной скоростью, прошел 14 км за 9 мин. Какова скорость автомобиля?
3. Задача. В классе 40 учеников. Из них  занимаются в спортивных секциях. Сколько учеников класса занимаются спортом?
занимаются в спортивных секциях. Сколько учеников класса занимаются спортом?
4. Решите уравнение:
а) б)
б) 
5. Какое число надо разделить на 6, чтобы частное равнялось  ?
?
Контрольная работа №9
Вариант I
1. Сравните числа: 7,195 и 12,1; 8,276 и 8,3; 0,76 и 0,7598
2. Выполните действия:
а) 12,3 + 5,26 в) 79,1-6,08
б) 0,48 + 0,057 г) 5-1,63
3. Округлите:
а) 3,18; 30,625; 257,51; 0,28 до единиц
б) 0,531; 12,467; 8,5452 и 0,009 до сотых
4. Задача. Собственная скорость лодки 3,4 км/ч. Скорость лодки против течения реки 0,8 км/ч. Найдите скорость лодки по течению.
5. Запишите четыре значения m, при которых верно неравенство 0,71m
Вариант II
1. Сравните числа: 8,2 и 6,984; 7,6 и 7,596; 0,6387 и 0,64
2. Выполните действия:
а) 15,4+3,18 в) 86,3 – 5,07
в) 0,068+0,39 г) 7 – 2,78
3. Округлите:
а) 8,72; 40,198; 164,53 и 0,61 до единиц
б) 0,834; 19,471; 6,352 и 0,08 до десятых.
4. Задача. Собственная скорость катера 32,8 км/ч. Скорость катера по течению реки 34,2 км/ч. Найдите скорость катера против течения.
5. Запишите четыре значения n, при которых верно неравенство 0,65n
Контрольная работа №10
Вариант I
1. Вычислите:
а) 4,35∙18 г) 53,3:26
б) 6,25∙108 д) 6:24
в) 126,385∙10 е) 126,385:100
2. Решить уравнение:
7у+2,6=27,8
3. Найдите значение выражения
90-16,2:9+0,08
4. Задача. На автомобиль погрузили 6 контейнеров и 8 одинаковых ящиков по 0,28т каждый. Какова масса одного ящика, если масса всего груза 2,4т?
5. Задача. Как изменится произведение двух десятичных дробей, если в одном множителе перенести запятую вправо через две цифры, а в другом – влево через четыре цифры?
Вариант II
1. Вычислите:
а) 3,85∙24; г) 35,7:34
б) 4,75∙116; д) 7:28
в) 234,166∙100 е) 234,166:10
2. Решить уравнение:
6х+3,8=20,6
3. Найдите значение выражения
40-23,2:8+0,07
4. Задача. Из 7,7м ткани сшили 7 платьев для кукол и 9 одинаковых полотенец. Сколько ткани пошло на одно полотенце, если на каждое платье потребовалось 0,65 м ткани?
5. Задача. Как изменится произведение двух десятичных дробей, если в одном множителе перенести запятую влево через четыре цифры, а в другом - вправо через две цифры?
Контрольная работа №11
Вариант I
1. Выполните действия:
а) 0,872∙6,3 г) 30,42:7,8
б) 1,6∙7,625 д) 0,702:0,065
в) 0,045∙0,1 е) 0,026:0,01
2. Найдите среднее арифметическое чисел 32,4; 41; 27,95; 46,9; 55,75.
3. Найдите значение выражения 296,2 – 2,7∙6,6 + 6:0,15.
4. Задача. Поезд 3ч шел со скоростью 63,2 км/ч и 4ч со скоростью 76,5 км/ч. Найдите среднюю скорость поезда на всем пути.
5. Задача. Сумма трех чисел 10,23, а среднее арифметическое шести других чисел 2,9. Найти среднее арифметическое всех этих девяти чисел.
Вариант II
1. Выполните действия:
а) 0,964∙7,4 г) 25,23:8,7
б) 2,4∙7,375 д) 0,0918:0,0085
в) 0,72∙0,01 е) 0,39:0,1
2. Найдите среднее арифметическое чисел 63; 40,63; 70,4; 67,97
3. Найдите значение выражения 398,6 – 3,8∙7,7 + 3:0,06
4. Задача. Легковой автомобиль шел 2ч со скоростью 55,4 км/ч и ещё 4ч со скоростью 63,5 км/ч. Найдите среднюю скорость автомобиля на всем пути.
5. Задача. Среднее арифметическое пяти чисел 4,7, а сумма других трех чисел 25,14. Найдите среднее арифметическое всех этих восьми чисел.
Контрольная работа №12
Вариант I
1. Задача. Площадь поля 260 га. Горохом засеяно 35% поля. Какую площадь занимают посевы гороха?
2. Найдите значение выражения 201 – (176,4:16,8+9,68)∙2,5.
3. Задача. В библиотеке 12% всех книг – словари. Сколько книг в библиотеке, если словарей в ней 900?
4. Решите уравнение 12+8,3х+1,5х = 95,3
5. Задача. От мотка провода отрезали сначала 30%, а затем ещё 60% остатка. После этого в мотке осталось 42 м провода. Сколько метров провода было в мотке первоначально?
Вариант II
1. Задача. В железной руде содержится 45% железа. Сколько тонн железа содержится в 380 т руды?
2. Найдите значение выражения (299,3:14,6 – 9,62)∙3,5+72,2
3. Задача. За день вспахали 18% поля. Какова площадь всего поля, если вспахали 1170 га?
4. Решите уравнение 6,7у+13+3,1у=86,5
5. Задача. Израсходовали сначала 40% имевшихся денег, а затем ещё 30% оставшихся. После этого осталось 105р. Сколько было денег первоначально?
Контрольная работа №13
Вариант I
1. Постройте углы, если:
а) о б) о
2. Начертите треугольник AKN такой, чтобы A = 120о. Измерьте и запишите градусные меры остальных углов треугольника.
3. Луч ОК делит прямой угол DOS на два угла так, что угол DOK составляет 0,7 угла DOS. Найдите градусную меру угла KOS.
4. Развернутый угол AMF разделен лучом МС на два угла АМС и CMF. Найдите градусные меры этих углов, если угол АМС вдвое больше угла CMF.
5. Из вершины развернутого угла DKP проведены его биссектриса КВ и луч КМ так, что о. Какой может быть градусная мера угла DKM?
Вариант II
1. Постройте углы, если:
а) ADF = 110o б) HON = 73o
2. Начертите треугольник BCF такой, чтобы о. Измерьте и запишите градусные меры остальных углов треугольника.
3. Луч АР делит прямой угол CAN на два угла так, что угол NAP составляет 0,3 угла CAN. Найдите градусную меру угла РАС.
4. Развернутый угол ВОЕ разделен лучом ОТ на два угла ВОТ и ТОЕ. Найдите градусные меры этих углов, если угол ВОТ втрое меньше угла ТОЕ.
5. Из вершины развернутого угла MNR проведены его биссектриса NB и луч NP так, что BNP = 26o. Какой может быть градусная мера угла MNP?
Контрольная работа №14
Вариант I
1. Вычислите: 2,66:3,8 – 0,81∙0,12 + 0,0372
2. В магазине 240 кг фруктов. За день продали 65% фруктов. Сколько килограммов фруктов осталось.
3. Найдите высоту прямоугольного параллелепипеда, объем которого равен 25,2 дм3, длина 3,5 дм и ширина 16 см.
4. Собственная скорость теплохода 24,5 км/ч, скорость течения реки 1,3 км/ч. Сначала теплоход 0,4 ч плыл по озеру, а затем 3,5 ч по реке против течения. Какой путь прошел теплоход за все это время?
5. Постройте углы МОК и КОС, если о, о. Какой может быть градусная мера угла СОМ?
Вариант II
1. Вычислите: 7,8∙0,26 – 2,32:2,9 + 0,672.
2. В цистерне 850 л молока. 48% молока разлили в бидоны. Сколько литров молока осталось в цистерне?
3. Объем прямоугольного параллелепипеда равен 1,35 м3, высота 2,25 м и длина 8 дм. Найдите его ширину.
4. Катер плыл 3,5 ч по течению реки и 0,6 ч по озеру. Найдите путь, пройденный катером за все это время, если собственная скорость катера 16,5 км/ч, а скорость течения реки 2,1 км/ч.
5. Постройте углы AND и NDB, если ADN = 34o, NDB = 120o. Какой может быть градусная мера угла ADB?
Итоговая контрольная работа
Вариант I
1. Вычислите: 8,45 + (346 – 83,6):12,8
2. Вычислите площадь прямоугольника, если его ширина 1,9 дм, а длина вдвое больше.
3. Катер шел 3ч против течения реки и 2ч по течению. Какой путь прошел катер за эти 5ч, если собственная скорость катера 18,6 км/ч, а скорость течения реки 1,3 км/ч?
4. Начертите треугольник АОВ, в котором угол АОВ равен 75о.
5. В классе 30 учеников. Оценку «5» на экзамене получили 30% учеников. Сколько учеников получили на экзамене пятерки?
Вариант II
1. Вычислите 6,35 + (359 – 63,8):14,4.
2. Длина прямоугольника 12,6 см, а ширина втрое меньше. Найдите площадь этого прямоугольника.
3. Собственная скорость моторной лодки 6,7 км/ч. Скорость течения реки 1,2 км/ч. Лодка шла 2ч против течения и 2ч по течению реки. Какой путь прошла моторная лодка за эти 4ч?
4. Начертите треугольник ВСК, в котором угол ВСК равен 110о.
5. Площадь поля 120 га. Тракторист вспахал 70% поля. Сколько гектаров земли вспахал тракторист?
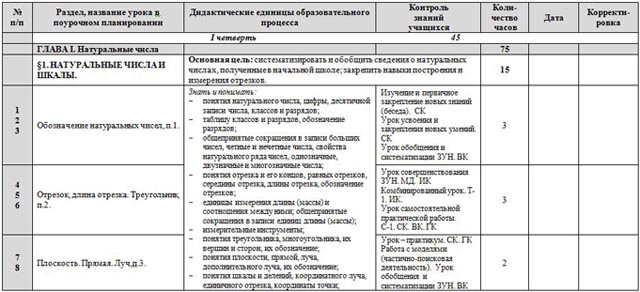

 Получите свидетельство
Получите свидетельство Вход
Вход


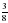 ), М(
), М(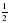 ), К(
), К(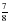 ), Т(
), Т(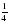 ), Р(
), Р(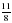 )
)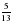 и
и 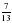 , б)
, б) 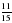 и
и 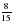 , в) 1 и
, в) 1 и 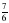 , г)
, г) 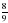 и
и 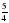
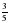 числа 30 и
числа 30 и 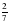 числа 14.
числа 14.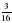 его периметра. Найдите длину этого прямоугольника.
его периметра. Найдите длину этого прямоугольника.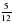 ), С(
), С(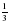 ), О(
), О(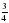 ), Н(
), Н(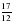 )
)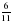 и
и 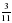 , б)
, б)  и
и 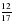 , в) 1 и
, в) 1 и 








 Рабочая программа по математике (5 класс) (0.17 MB)
Рабочая программа по математике (5 класс) (0.17 MB)
 0
0 635
635 64
64 Нравится
0
Нравится
0






