Краснодарский край, Выселковский район, станица Выселки
Муниципальное бюджетное общеобразовательное учреждение
средняя общеобразовательная школа №17
имени воина-интернационалиста Величко Александра Алексеевича
станицы Выселки муниципального образования Выселковский район
УТВЕРЖДЕНО
решением педагогического совета
от 29 августа 2015 года
протокол № 1
Председатель _______ Е.А.Беспалова
РАБОЧАЯ ПРОГРАММА
По математике
Уровень образования (класс) основное общее образование, 5-9 классы
Количество часов 850
Учитель Борисова Марина Минигарифовна
Программа разработана на основе программы по математике, включенной в содержательный раздел основной образовательной программы основного общего образования МБОУ СОШ №17 ст. Выселки, утвержденной педагогическим советом МБОУ СОШ №17 ст.Выселки , протокол № 1 от 29 августа 2015 года
Пояснительная записка.
Рабочая программа составлена в соответствии со следующими нормативными и распорядительными документами:
1. Закон «Об образовании в Российской Федерации» от 29.12. 2012 года № 273-ФЗ.
2. Закон Краснодарского края от 16 июля 2013 г. N 2770-КЗ "Об образовании в Краснодарском крае" (с изменениями и дополнениями)
3. Приказ Министерства образования РФ от 05.03. 2004 г. N 1089 «Об утверждении федерального компонента государственных образовательных стандартов начального общего, основного общего и среднего (полного) общего образования», с изменениями и дополнениями.
4. Приказ Министерства образования и науки РФ от 06.10. 2009 г. № 373 «Об утверждении и введении в действие федерального государственного образовательного стандарта начального общего образования», с изменениями и дополнениями.
5. Приказ Министерства образования и науки РФ от 29.12. 2014 г. № 1643 «О внесении изменений в приказ Министерства образования и науки Российской Федерации от 06.10. 2009 г. № 373 «Об утверждении и введении в действие федерального государственного образовательного стандарта начального общего образования»»
6. Приказ Министерства образования и науки РФ от 17.12. 2010 г. № 1897 «Об утверждении федерального государственного образовательного стандарта основного общего образования».
7. Приказ Министерства образования и науки РФ от 29.12. 2014 г. № 1644 «О внесении изменений в приказ Министерства образования и науки Российской Федерации от 17.12. 2010 г. № 1897 «Об утверждении федерального государственного образовательного стандарта основного общего образования».
8. Письмо Департамента государственной политики в образовании Министерства образования и науки РФ от 07.07. 2005 г. N 03-1263 «О примерных программах по учебным предметам федерального базисного учебного плана»,
9. Приказ Министерства образования и науки Российской Федерации от 30.08.2013 № 1015 (с изм. и дополнениями) «Об утверждении Порядка организации и осуществления образовательной деятельности по основным общеобразовательным программам - образовательным программам начального общего, основного общего
и среднего общего образования»
10. Приказ Министерства образования и науки Российской Федерации от 31.03. 2014 г. № 253 «Об утверждении федерального перечня учебников, рекомендуемых к использованию при реализации имеющих государственную аккредитацию образовательных программ начального общего, основного общего, среднего общего
образования»
11. Приказ Министерства образования и науки Российской Федерации от 08.06.2015 г. № 576 «О внесении изменений в федеральный перечень учебников, рекомендуемых к использованию при реализации имеющих государственную аккредитацию образовательных программ начального общего, основного общего, среднего
общего образования, утвержденный приказом Министерства образования и науки Российской Федерации от 31 марта 2014 г. № 253»
12. Постановление Федеральной службы по надзору в свете защиты прав потребителей и благополучия человека, Главного государственного санитарного врача РФ от 29.12. 2010 г. N 189 «Об утверждении СанПиН 2.4.2.2821-10 «Санитарно-эпидемиологические требования к условиям и организации обучения в общеобразовательных учреждениях», с изменениями.
13. Приказ Министерства образования и науки РФ от 04.10. 2010 г. № 986 «Об утверждении федеральных требований к образовательным учреждениям в части минимальной оснащённости учебного процесса и оборудования учебных помещений».
14. Письмо Министерства образования и науки РФ от 01.04. 2005 г. № 03-417 «О перечне учебного и компьютерного оборудования для оснащения общеобразовательных учреждений».
15. Письмо Министерства образования и науки РФ от 04.03. 2010 г. № 03-413 «О методических рекомендациях по реализации элективных курсов».
16. Рекомендации Министерства образования и науки РФ от 24.11. 2011 г. № МД-1552/03 «Об оснащении общеобразовательных учреждений учебным и учебно-лабораторным оборудованием».
17. Письмо министерства образования и науки Краснодарского края от 16.03. 2015 года № 47-3353/15-14 «О структуре основных образовательных программ общеобразовательных организаций».
18. Письмо министерства образования и науки Краснодарского края от 11.02.2014года № 47-1806/14-14 «О перечне профилей обучения, открываемых в общеобразовательных организациях в 2014-2015 учебном году».
19. Приказ департамента образования и науки Краснодарского края от 27.02.2012г. № 802 «Об утверждении перечня образовательных учреждений края, являющихся пилотными площадками по введению федерального государственного образовательного стандарта основного общего образования».
20. Письмо министерства образования и науки Краснодарского края от 14.07.2015г. № 47-10267/ 15-14 «О формировании учебных планов общеобразовательных организаций Краснодарского края на 2015-2016 учебный год»
21. Приказ министерства образования и науки Краснодарского края от 11.02.2013г. № 714 «Об утверждении перечня образовательных учреждений края, являющихся пилотными площадками по введению федерального государственного образовательного стандарта основного общего образования с 01.09. 2013 года».
22. Примерные основные образовательные программы начального общего образования и основного общего образования, внесенных в реестр образовательных программ, одобренных федеральным учебно-методическим объединением по общему образованию (протокол от 8 апреля 2015г. № 1/5). http://fgosreestr.ru/.
23. Письмо министерства образования и науки Краснодарского края от 17.07.2015 года № 47-10474/15-14 «О рекомендациях по составлению рабочих программ учебных предметов, курсов и календарно-тематического планирования»
- с учетом Приказа Минздравсоцразвития России от 26 августа 2010 г. № 761н. «Об утверждении Единого квалификационного справочника должностей руководителей, специалистов и служащих»
- на основе Примерных программ по учебным предметам. Математика. 5-9 классы.-3-е изд., перераб.- М.: Просвещение, 2011.-64с.- (Стандарты второго поколения).
- программы по математике, включенной в содержательный раздел основной образовательной программы основного общего образования МБОУ СОШ №17 ст. Выселки, утвержденной педагогическим советом МБОУ СОШ №17 ст.Выселки , протокол № 1 от 29 августа 2015 года,
обеспечена УМК для 5–6-го классов авторов Е.А. Бунимович, Г.В. Дорофеев, С.Б. Суворова и др., УМК для 7-9-го классов авторов Ю.Н.Макарычев и др. УМК 7-9-го классов авторов Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев.
Математика является одним из основных, системообразующих предметов школьного образования. Такое место математики среди школьных предметов обусловливает и её особую роль с точки зрения всестороннего развития личности учащихся. При этом когнитивная составляющая данного курса позволяет обеспечить как требуемый государственным стандартом необходимый уровень математической подготовки, так и повышенный уровень, являющийся достаточным для углубленного изучения предмета.
В основу настоящей программы положены педагогические и дидактические принципы вариативного развивающего образования, изложенные в концепции образовательной программы «Перспективная школа», и современные дидактико-психологические тенденции, связанные с вариативным развивающим образованием и требованиями ФГОС.
А. Личностно ориентированные принципы: принцип адаптивности; принцип развития; принцип комфортности процесса обучения.
Б. Культурно ориентированные принципы: принцип целостной картины мира; принцип целостности содержания образования; принцип систематичности; принцип смыслового отношения к миру; принцип ориентировочной функции знаний; принцип опоры на культуру как мировоззрение и как культурный стереотип.
В. Деятельностно ориентированные принципы: принцип обучения деятельности; принцип управляемого перехода от деятельности в учебной ситуации к деятельности в жизненной ситуации; принцип перехода от совместной учебно-познавательной деятельности к самостоятельной деятельности учащегося (зона ближайшего развития); принцип опоры на процессы спонтанного развития; принцип формирования потребности в творчестве и умений творчества.
Математическое образование является обязательной и неотъемлемой частью общего образования на всех ступенях школы. Обучение математике в основной школе направлено на достижение следующих целей:
1) в направлении личностного развития:
Формирование представлений о математике как части общечеловеческой культуры, о значимости математики в развитии цивилизации и современного общества;
Развитие логического и критического мышления, культуры речи, способности к умственному эксперименту;
Формирование интеллектуальной честности и объективности, способности к преодолению мыслительных стереотипов, вытекающих из обыденного опыта;
Воспитание качеств личности, обеспечивающих социальную мобильность, способность принимать самостоятельные решения;
Формирование качеств мышления, необходимых для адаптации в современном информационном обществе;
Развитие интереса к математическому творчеству и математических способностей;
2) в метапредметном направлении:
Развитие представлений о математике как форме описания и методе познания действительности, создание условий для приобретения первоначального опыта математического моделирования;
Формирование общих способов интеллектуальной деятельности, характерных для математики и являющихся основой познавательной культуры, значимой для различных сфер человеческой деятельности;
3) в предметном направлении:
Овладение математическими знаниями и умениями, необходимыми для продолжения образования, изучения смежных дисциплин, применения в повседневной жизни;
Создание фундамента для математического развития, формирования механизмов мышления, характерных для математической деятельности.
В организации учебно – воспитательного процесса важную роль играют задачи. Они являются и целью, и средством обучения. Важным условием правильной организации этого процесса является выбор рациональной системы методов и приемов обучения, специфики решаемых образовательных и воспитательных задач.
Целью изучения курса математике в 5-6 классах является систематическое развитие понятия числа, выработка умений выполнять устно и письменно арифметические действия над числами, переводить практические задачи на язык математики, подготовка учащихся к изучению систематических курсов алгебры и геометрии. Курс строится на индуктивной основе с привлечением элементов дедуктивных рассуждений. В ходе изучения курса учащиеся развивают навыки вычислений с натуральными числами, овладевают навыками с обыкновенными и десятичными дробями, положительными и отрицательными числами, получают представление об использовании букв для записи выражений и свойств арифметических действий, составлении уравнений, продолжают знакомство с геометрическими понятиями, приобретают навыки построения геометрических фигур.
Целью изучения курса математике в 7 - 9 классах является развитие вычислительных умений до уровня, позволяющего уверенно использовать их при решении задач математики и смежных предметов, усвоение аппарата уравнений и неравенств как основного средства математического моделирования задач, осуществление функциональной подготовки школьников. Курс характеризуется повышением теоретического уровня обучения, постепенным усилием роли теоретических обобщений и дедуктивных заключений. Прикладная направленность раскрывает возможность изучать и решать практические задачи.
Целью изучения курса геометрии в 7-9 классах является систематическое изучение свойств геометрических фигур на плоскости, формирование пространственных представлений, развитие логического мышления и подготовка аппарата, необходимого для изучения смежных дисциплин и курса стереометрии в старших классах.
В основе построения данного курса лежит идея гуманизации обучения, соответствующая современным представлениям о целях школьного образования и уделяющая особое внимание личности ученика, его интересам и способностям.
Предлагаемый курс позволяет обеспечить формирование как предметных умений, так и универсальных учебных действий школьников, а также способствует достижению определённых во ФГОС личностных результатов, которые в дальнейшем позволят учащимся применять полученные знания и умения для решения различных жизненных задач.
II. Общая характеристика учебного предмета «Математика»
Настоящая программа по математике для основной школы является логическим продолжением программы «Перспективная школа» для начальной школы и вместе с ней составляет описание непрерывного курса математики с 1-го по 9-й класс общеобразовательной школы.
В основе содержания обучения математике лежит овладение учащимися следующими видами компетенций: предметной, коммуникативной, организационной и общекультурной. В соответствии с этими видами компетенций выделены главные содержательно-целевые направления развития учащихся средствами предмета «Математика».
Предметная компетенция. Под предметной компетенцией понимается осведомлённость школьников о системе основных математических представлений и овладение ими необходимыми предметными умениями. Формируются следующие образующие эту компетенцию представления: о математическом языке как средстве выражения математических законов, закономерностей и т.д.; о математическом моделировании как одном из важных методов познания мира. Формируются следующие образующие эту компетенцию умения: создавать простейшие математические модели, работать с ними и интерпретировать полученные результаты; приобретать и систематизировать знания о способах решения математических задач, а также применять эти знания и умения для решения многих жизненных задач.
Коммуникативная компетенция. Под коммуникативной компетенцией понимается сформированность умения ясно и чётко излагать свои мысли, строить аргументированные рассуждения, вести диалог, воспринимая точку зрения собеседника и в то же время подвергая её критическому анализу, отстаивать (при необходимости) свою точку зрения, выстраивая систему аргументации. Формируются образующие эту компетенцию умения, а также умения извлекать информацию из разного рода источников, преобразовывая её при необходимости в другие формы (тексты, таблицы, схемы и т.д.).
Организационная компетенция. Под организационной компетенцией понимается сформированность умения самостоятельно находить и присваивать необходимые учащимся новые знания. Формируются следующие образующие эту компетенцию умения: самостоятельно ставить учебную задачу (цель), разбивать её на составные части, на которых будет основываться процесс её решения, анализировать результат действия, выявлять допущенные ошибки и неточности, исправлять их и представлять полученный результат в форме, легко доступной для восприятия других людей.
Общекультурная компетенция. Под общекультурной компетенцией понимается осведомленность школьников о математике как элементе общечеловеческой культуры, её месте в системе других наук, а также её роли в развитии представлений человечества о целостной картине мира. Формируются следующие образующие эту компетенцию представления: об уровне развития математики на разных исторических этапах; о высокой практической значимости математики с точки зрения создания и развития материальной культуры человечества, а также о важной роли математики с точки зрения формировании таких важнейших черт личности, как независимость и критичность мышления, воля и настойчивость в достижении цели и др.
Содержание математического образования в основной школе формируется на основе фундаментального ядра школьного математического образования. В программе оно представлено в виде совокупности содержательных разделов, конкретизирующих соответствующие блоки фундаментального ядра применительно к основной школе. Программа регламентирует объем материала, обязательного для изучения в основной школе, а также дает его распределение между 5—6 и 7—9 классами.
Содержание математического образования в основной школе включает следующие разделы: арифметика, алгебра, функции, вероятность и статистика, геометрия. Наряду с этим в него включен дополнительный раздел: математика в историческом развитии, что связано с реализацией целей общеинтеллектуального и общекультурного развития учащихся. Содержание раздела разворачивается в содержательно-методическую линию, пронизывающую все основные разделы содержания математического образования на данной ступени обучения.
Содержание раздела «Арифметика» служит базой для дальнейшего изучения учащимися математики, способствует развитию их логического мышления, формированию умения пользоваться алгоритмами, а также приобретению практических навыков, необходимых в повседневной жизни. Развитие понятия о числе в основной школе связано с рациональными и иррациональными числами, формированием первичных представлений о действительном числе. Завершение числовой линии (систематизация сведений о действительных числах, о комплексных числах), так же как и более сложные вопросы арифметики (алгоритм Евклида, основная теорема арифметики), отнесено к ступени общего среднего (полного) образования.
Содержание раздела «Алгебра» направлено на формирование у учащихся математического аппарата для решения задач из разных разделов математики, смежных предметов, окружающей реальности. Язык алгебры подчеркивает значение математики как языка для построения математических моделей процессов и явлений реального мира. В задачи изучения алгебры входят также развитие алгоритмического мышления, необходимого, в частности, для усвоения курса информатики, овладения навыками дедуктивных рассуждений. Преобразование символьных форм вносит специфический вклад в развитие воображения учащихся, их способностей к математическому творчеству. В основной школе материал группируется вокруг рациональных выражений, а вопросы, связанные с иррациональными выражениями, с тригонометрическими функциями и преобразованиями, входят в содержание курса математики на старшей ступени обучения в школе.
Содержание раздела «Функции» нацелено на получение школьниками конкретных знаний о функции как важнейшей математической модели для описания и исследования разнообразных процессов. Изучение этого материала способствует развитию у учащихся умения использовать различные языки математики (словесный, символический, графический), вносит вклад в формирование представлений о роли математики в развитии цивилизации и культуры.
Раздел «Вероятность и статистика» — обязательный компонент школьного образования, усиливающий его прикладное и практическое значение. Этот материал необходим прежде всего для формирования у учащихся функциональной грамотности — умений воспринимать и критически анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей, проводить простейшие вероятностные расчеты. Изучение основ комбинаторики позволит учащимся рассматривать случаи, осуществлять перебор и подсчет числа вариантов, в том числе в простейших прикладных задачах.
При изучении статистики и вероятности расширяются представления о современной картине мира и методах его исследования, формируется понимание роли статистики как источника социально значимой информации и закладываются основы вероятностного мышления.
Цель содержания раздела «Геометрия» — развить у учащихся пространственное воображение и логическое мышление путем систематического изучения свойств геометрических фигур на плоскости и в пространстве и применения этих свойств при решении задач вычислительного и конструктивного характера. Существенная роль при этом отводится развитию геометрической интуиции. Сочетание наглядности со строгостью является неотъемлемой частью геометрических знаний. Материал, относящийся к блокам «Координаты» и «Векторы», в значительной степени несет в себе межпредметные знания, которые находят применение как в различных математических дисциплинах, так и в смежных предметах.
Особенностью раздела «Логика и множества» является то, что представленный в нем материал преимущественно изучается и используется распределенно – в ходе рассмотрения различных вопросов курса. Соответствующий материал нацелен на математическое развитие учащихся, формирование у них умения точно, сжато и ясно излагать мысли в устной и письменной речи.
Раздел «Математика в историческом развитии» предназначен для формирования представлений о математике как части человеческой культуры, для общего развития школьников, для создания культурно-исторической среды обучения. На него не выделяется специальных уроков, усвоение его не контролируется, но содержание этого раздела органично присутствует в учебном процессе как своего рода гуманитарный фон при рассмотрении проблематики основного содержания математического образования.
Ценностные ориентиры содержания учебного предмета.
Математическое образование играет важную роль как в практической, так и в духовной жизни общества. Практическая сторона математического образования связана с формированием способов деятельности, духовная — с интеллектуальным развитием человека, формированием характера и общей культуры.
Практическая полезность математики обусловлена тем, что ее предметом являются фундаментальные структуры реального мира: пространственные формы и количественные отношения — от простейших, усваиваемых в непосредственном опыте, до достаточно сложных, необходимых для развития научных и технологических идей. Без конкретных математических знаний затруднено понимание принципов устройства и использования современной техники, восприятие и интерпретация разнообразной социальной, экономической, политической информации, малоэффективна повседневная практическая деятельность. Каждому человеку в своей жизни приходится выполнять достаточно сложные расчеты, находить в справочниках нужные формулы и применять их, владеть практическими приемами геометрических измерений и построений, читать информацию, представленную в виду таблиц, диаграмм, графиков, понимать вероятностный характер случайных событий, составлять несложные алгоритмы и др.
Без базовой математической подготовки невозможно стать образованным современным человеком. В школе математика служит опорным предметом для изучения смежных дисциплин. В послешкольной жизни реальной необходимостью в наши дни является непрерывное образование, что требует полноценной базовой общеобразовательной подготовки, в том числе и математической. И наконец, все больше специальностей, где необходим высокий уровень образования, связано с непосредственным применением математики (экономика, бизнес, финансы, физика, химия, техника, информатика, биология, психология и др.). Таким образом, расширяется круг школьников, для которых математика становится значимым предметом.
Для жизни в современном обществе важным является формирование математического стиля мышления, проявляющегося в определенных умственных навыках. В процессе математической деятельности в арсенал приемов и методов человеческого мышления естественным образом включаются индукция и дедукция, обобщение и конкретизация, анализ и синтез, классификация и систематизация, абстрагирование и аналогия. Объекты математических умозаключений и правила их конструирования вскрывают механизм логических построений, вырабатывают умения формулировать, обосновывать и доказывать суждения, тем самым развивают логическое мышление. Ведущая роль принадлежит математике в формировании алгоритмического мышления и воспитании умений действовать по заданному алгоритму и конструировать новые. В ходе решения задач — основной учебной деятельности на уроках математики — развиваются творческая и прикладная стороны мышления.
Обучение математике дает возможность развивать у учащихся точную, экономную и информативную речь, умение отбирать наиболее подходящие языковые (в частности, символические, графические) средства.
Математическое образование вносит свой вклад в формирование общей культуры человека. Необходимым компонентом общей культуры в современном толковании является общее знакомство с методами познания действительности, представление о предмете и методе математики, его отличия от методов естественных и гуманитарных наук, об особенностях применения математики для решения научных и прикладных задач.
Изучение математики способствует эстетическому воспитанию человека, пониманию красоты и изящества математических рассуждений, восприятию геометрических форм, усвоению идеи симметрии.
История развития математического знания дает возможность пополнить запас историко-научных знаний школьников, сформировать у них представления о математике как части общечеловеческой культуры. Знакомство с основными историческими вехами возникновения и развития математической науки, с историей великих открытий, именами людей, творивших науку, должно войти в интеллектуальный багаж каждого культурного человека.
III. Описание места учебного предмета «Математика» в учебном плане
Согласно учебному плану МБОУ СОШ №17 имени воина-интернационалиста А. А. Величко ст. Выселки всего на изучение математики в основной школе отводится 5 учебных часов в неделю в течение каждого года обучения, всего 850 уроков.
В соответствии с требованиями Федерального государственного образовательного стандарта основного общего образования предмет «Математика» изучается с 5-го по 9-й класс в виде следующих учебных курсов: 5–6 класс – «Математика» (интегрированный предмет), 7–9 классах предмет «Математика» (Алгебра и Геометрия).
Распределение учебного времени между этими предметами представлено в таблице.
| Классы | Предметы математического цикла | Количество часов на ступени основного образования
|
| 5-6 | Математика | 340
|
| 7-9 | Математика (Алгебра) | 306
|
| Математика (Геометрия) | 204
|
| Всего | 850 |
Предмет «Математика» в 5—6 классах включает арифметический материал, элементы алгебры и геометрии, а также элементы вероятностно-статистической линии.
Предмет «Алгебра» включает некоторые вопросы арифметики, развивающие числовую линию 5—6 классов, собственно алгебраический материал, элементарные функции, а также элементы вероятностно-статистической линии.
В рамках учебного предмета «Геометрия» традиционно изучаются евклидова геометрия, элементы векторной алгебры, геометрические преобразования.
Изучение вероятностно-статистического материала отнесено к 5—6, к 7—9 классам
IV. Личностные, метапредметные и предметные результаты освоения учебного предмета «Математика»
Изучение математики в основной школе дает возможность обучающимся достичь следующих результатов развития:
I В личностном направлении:
• умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры;
критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта;
представление о математической науке как сфере человеческой деятельности, об этапах ее развития, о ее значимости для развития цивилизации;
креативность мышления, инициатива, находчивость, активность при решении математических задач;
умение контролировать процесс и результат учебной математической деятельности;
способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений;
I I В метапредметном направлении:
первоначальные представления об идеях и о методах математики как универсальном языке науки и техники, средстве моделирования явлений и процессов;
умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;
умение находить в различных источниках информацию, необходимую для решения математических проблем, представлять ее в понятной форме, принимать решение в условиях неполной и избыточной, точной и вероятностной информации;
умение понимать и использовать математические средства наглядности (графики, диаграммы, таблицы, схемы и др.) для иллюстрации, интерпретации, аргументации;
умение выдвигать гипотезы при решении учебных задач, понимать необходимость их проверки;
умение применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач;
понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом;
умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем;
умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера;
Ш В предметном направлении:
овладение базовым понятийным аппаратом по основным разделам содержания, представление об основных изучаемых понятиях (число, геометрическая фигура, уравнение, функция, вероятность) как важнейших математических моделях, позволяющих описывать и изучать реальные процессы и явления;
умение работать с математическим текстом (анализировать, извлекать необходимую информацию), грамотно применять математическую терминологию и символику, использовать различные языки математики;
умение проводить классификации, логические обоснования, доказательства математических утверждений;
умение распознавать виды математических утверждений (аксиомы, определения, теоремы и др.), прямые и обратные теоремы;
развитие представлений о числе и числовых системах от натуральных до действительных чисел, овладение навыками устных, письменных, инструментальных вычислений;
овладение символьным языком алгебры, приемами выполнения тождественных преобразований рациональных выражений, решения уравнений, систем уравнений, неравенств и систем неравенств, умение использовать идею координат на плоскости для интерпретации уравнений, неравенств, систем, умение применять алгебраические преобразования, аппарат уравнений и неравенств для решения задач из различных разделов курса;
овладение системой функциональных понятий, функциональным языком и символикой, умение на основе функционально-графических представлений описывать и анализировать реальные зависимости;
овладение основными способами представления и анализа статистических данных; наличие представлений о статистических закономерностях в реальном мире и о различных способах их изучения, о вероятностных моделях;
овладение геометрическим языком, умение использовать его для описания предметов окружающего мира, развитие пространственных представлений и изобразительных умений, приобретение навыков геометрических построений;
усвоение систематических знаний о плоских фигурах и их свойствах, а также на наглядном уровне — о простейших пространственных телах, умение применять систематические знания о них для решения геометрических и практических задач;
умения измерять длины отрезков, величины углов, использовать формулы для нахождения периметров, площадей и объемов геометрических фигур;
умение применять изученные понятия, результаты, методы для решения задач практического характера и задач из смежных дисциплин с использованием при необходимости справочных материалов, калькулятора, компьютера.
V. Содержание учебного предмета «Математика»
Таблица распределения часов:
| Раздел | Количество часов |
| Примерная программа | Рабочая программа | Рабочая программа по классам |
|
| 5 кл | 6 кл | 7 кл | 8кл | 9кл |
| Натуральные числа | 50 | 50 | 50 |
|
|
|
|
| Дроби | 120 | 120 | 54 | 66 |
|
|
|
| Рациональные числа | 40 | 40 |
| 40 |
|
|
|
| Измерения, приближения, оценки. Зависимости между величинами | 30 | 30 | 20 |
|
| 10 |
|
| Элементы алгебры | 25 | 25 |
| 25 |
|
|
|
| Описательная статистика. Вероятность. Комбинаторика. Множества. | 20 | 20 | 12 | 8 |
|
|
|
| Наглядная геометрия | 45 | 45 | 25 | 20 |
|
|
|
| Действительные числа | 15 | 15 |
|
|
| 15 |
|
| Алгебраические выражения | 90 | 90 |
|
| 56 | 30 | 4 |
| Уравнения | 65 | 65 |
|
| 22 | 22 | 21 |
| Неравенства | 20 | 20 |
|
|
| 10 | 10 |
| Зависимости между величинами | 13 | 13 |
|
| 6 |
| 7 |
| Числовые функции | 25 | 25 |
|
| 8 | 5 | 12 |
| Числовые последовательности. | 15 | 15 |
|
|
|
| 15 |
| Описательная статистика | 5 | 5 |
|
| 5 |
|
|
| Случайные события и вероятность | 5 | 5 |
|
|
| 5 |
|
| Элементы комбинаторики и теории вероятностей | 8 | 8 |
|
|
|
| 8 |
| Множества. Элементы логики | 5 | 5 |
|
|
|
| 5 |
| Геометрические фигуры | 102 | 102 |
|
| 40 | 50 | 12 |
| Измерение геометрических величин | 35 | 35 |
|
| 5 | 10 | 20 |
| Построение с помощью циркуля и линейки | 17 | 17 |
|
| 15 | 2 |
|
| Геометрические преобразования | 10 | 10 |
|
|
| 2 | 8 |
| Координаты | 10 | 10 |
|
|
|
| 10 |
| Векторы | 10 | 10 |
|
|
|
| 10 |
| Резерв | 95 | 70 | 9 | 11 | 13 | 9 | 28 |
| ИТОГО | 875ч | 850ч | 170 | 170 | 170 | 170 | 170 |
Контрольные работы.
| 5 класс | 6 класс | 7 класс (алгебра) | 7 класс (геометрия) | 8 класс (алгебра) | 8 класс (геометрия) | 9 класс (алгебра) | 9 класс (геометрия) |
| 12 | 12 | 9 | 5 | 9 | 5 | 8 | 5 |
5-6 класс. МАТЕМАТИКА (340 часов)
Натуральные числа (50 ч.)
Как записывают и читают числа. Римская нумерация. Десятичная нумерация. Натуральный ряд. Арифметические действия с натуральными числами. Сложение натуральных чисел. Свойства нуля при сложении. Вычитание натуральных чисел как действие, обратной сложению. Свойства нуля при вычитании. Прикидка и оценка суммы. Умножение натуральных чисел. Свойства нуля и единицы при умножении. Деление натуральных чисел как действие, обратное умножению. Свойства нуля и единицы при делении. Числовые выражения. Вычисление значений числовых выражений. Порядок действий в числовых выражениях. Использование скобок. Составление и запись числовых выражений. Степень числа. Возведение натурального числа в степень. Квадрат числа, куб числа. Вычисление значений выражений, содержащих степень. Решение текстовых задач арифметическим способом. Свойства сложения. Свойства умножения. Переместительное свойство. Сочетательное свойство. Удобные вычисления. Распределительное свойство умножения относительно сложения. Преобразование числовых выражений. Примеры вычислений с использованием распределительного свойства. Решение задач на части. Задачи на уравнивание. Делители числа. Кратные числа. Простые числа. Составные числа и число 1. Решето Эратосфена. Разложение натурального числа на простые множители. Наибольший общий делитель, наименьшее общее кратное. Свойства делимости. Делимость произведения. Делимость суммы. Контрпример. Признаки делимости на 10, на 5, на 2. Признаки делимости на 9 и на 3. Деление с остатком. Примеры деления чисел с остатком.
Дроби (120 ч.)
Деление целого на доли. Обыкновенные дроби. Правильные и неправильные дроби. Изображение дробей точками на координатной прямой. Основное свойство дроби. Равные дроби. Приведение дроби к новому знаменателю. Сокращение дробей. Сравнение дробей с одинаковыми знаменателями. Приведение дробей к общему знаменателю. Сравнение дробей с разными знаменателями. Некоторые другие приемы сравнения дробей. Деление и дроби. Представление натуральных чисел дробями.
Сложение дробей с одинаковыми знаменателями. Вычитание дробей с одинаковыми знаменателями. Сложение дробей с разными знаменателями. Вычитание дробей с разными знаменателями. Смешанная дробь. Выделение целой части из неправильной дроби. Представление смешанной дроби в виде неправильной. Сложение смешанных дробей. Вычитание смешанных дробей. Правило умножения дробей. Умножение дроби на натуральное число. Умножение на смешанную дробь. Взаимообратные дроби. Правило деления дробей. Разные действия с дробями. Нахождение части от целого. Нахождение целого по его части. Задачи на совместную работу. Задачи на движение.
Дробь, числитель и знаменатель дроби. Основное свойство дроби. Приведение дроби к новому знаменателю. Сокращение дробей. Правила действий с дробями: сложение, вычитание, умножение, деление дробей. Задачи на совместную работу. «Многоэтажные» дроби. Нахождение части от числа. Нахождение числа по его части. Какую часть одно число составляет от другого. Понятие процента. Решение задач на нахождение процента от величины, на увеличение величины на несколько процентов. Особенности представления данных на столбчатых и круговых диаграммах. Построение диаграмм.
Десятичная запись чисел. Десятичные дроби. Представление десятичной дроби в виде обыкновенной и обыкновенной в виде десятичной. Изображение десятичных дробей точками на координатной прямой. Десятичные дроби и метрическая система мер. Признак обратимости обыкновенной дроби в десятичную. Десятичные представления некоторых обыкновенных дробей. Выражение величин дробями. Равные десятичные дроби. Сравнение и упорядочивание десятичных дробей. Сравнение обыкновенной дроби и десятичной.
Сложение десятичных дробей. Вычитание десятичных дробей. Действия с обыкновенными и десятичными дробями. Решение задач. Умножение десятичной дроби на единицу с нулями. Деление десятичной дроби на единицу с нулями. Переход от одних единиц измерения к другим. Умножение десятичной дроби на десятичную дробь. Умножение десятичной дроби на натуральное число. Возведение десятичной дроби в квадрат и куб, умножение десятичной дроби на обыкновенную. Разные действия с десятичными дробями. Решение задач. Случай, когда частное выражается десятичной дробью (деление десятичной дроби на натуральное число, на десятичную дробь). Пропорция. Основное свойство пропорции. Вычисление частного десятичных дробей в общем случае. Решение задач на движении. Что значит округлить десятичную дробь. Правило округления десятичных дробей. Приближённое частное.
Отношение двух чисел. Деление в данном отношении. Решение задач на деление в данном отношении. Выражение отношения в процентах. Масштаб. Представление процента десятичной дробью. Выражение дроби в процентах. Выражение дроби в процентах. Нахождение процентов от величины. Нахождение величины по её проценту. Решение текстовых задач арифметическими способами.
Рациональные числа (40 ч.)
Числа, противоположные натуральным. Множество целых чисел. Ряд целых чисел. Изображение целых чисел точками на координатной прямой. Сравнение и упорядочивание целых чисел. Сложение целых чисел одного знака, разных знаков. Сумма противоположных чисел. Вычисление суммы нескольких целых чисел. Вычисление числовых значений буквенных выражений. Правило нахождения разности двух целых чисел. Вычисление значений выражений, содержащих только действия сложения и вычитания. Вычисление значений буквенных выражений. Умножение целых чисел. Деление целых чисел. Разные действия с целыми числами.
Рациональные числа: положительные и отрицательные числа (целые и дробные); противоположные числа. Множество рациональных чисел. Изображение рациональных чисел точками координатной прямой. Сравнение рациональных чисел с помощью координатной прямой. Установление отношений «больше» («меньше») между рациональными числами. Понятие модуля числа. Арифметические действия с рациональными числами. Правила сложения рациональных чисел одного знака, разных знаков. Свойства арифметических действий. Свойства сложения, свойство нуля при сложении. Вычитание рациональных чисел. Умножение и деление рациональных чисел, правила знаков при умножении и делении. Свойства умножения, свойства 0, 1 и -1 при умножении. Равенство 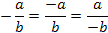 и его применение при вычислениях. Увеличение и уменьшение величины на несколько процентов. Округление и прикидка. Нахождение процентного отношения. Решение текстовых задач.
и его применение при вычислениях. Увеличение и уменьшение величины на несколько процентов. Округление и прикидка. Нахождение процентного отношения. Решение текстовых задач.
Измерения, приближения, оценки. (20 ч.)
Округление натуральных чисел. Единицы измерения длины, массы, времени, скорости. Движения в противоположных направлениях, скорость сближения, скорость удаления. Движение по реке, скорость движения по течению, против течения. Примеры зависимостей между величинами скорость, время, расстояние; производительность, время, работа; цена, количество, стоимость и др. Представление зависимостей в виде формул. Вычисления по формулам. Решение текстовых задач арифметическими способами. Окружность и круг. Радиус и диаметр окружности. Диагональ многоугольника. Выпуклые многоугольники. Равные фигуры. Признаки равенства. Единицы измерения площадей. Площадь фигуры. Площадь прямоугольника. Площадь арены цирка. Развёртка прямоугольного параллелепипеда и пирамиды. Объем прямоугольного параллелепипеда. Единицы измерения объема.
Элементы алгебры (25 ч.)
Математические выражения. Использование букв для обозначения чисел; для записи свойств арифметических действий. Буквенные выражения. Математические предложения. Числовое значение буквенного выражения. Допустимые выражения букв в выражении. Составление выражения по условию задачи с буквенными данными. Некоторые геометрические формулы. Формула стоимости. Формула пути. Число π. Формула длины окружности. Формула площади круга. Формула объёма шара. Вычисление размеров фигур, ограниченных окружностями и их дугами. Вычисления, связанные с цилиндром и шаром. Уравнение, корень уравнения. Решение уравнений. Нахождение неизвестных компонентов арифметических действий. Решение задач с помощью уравнений. Примеры различных систем координат в окружающем мире.
Декартовы координаты на плоскости. Прямоугольная система координат на плоскости, координаты точки. Построение точки по ее координатам, определение координат точки на плоскости. Неравенство треугольника. Цилиндр, конус, шар. Сечение. Задачи на разрезание и составление фигур. Геометрия на клетчатой бумаге. Призмы. Параллелепипед. Развёртка призмы. Призмы в архитектуре.
Описательная статистика. Вероятность. Комбинаторика. Множества (20 ч.)
Как устроены таблицы. Чтение таблиц. Как составлять таблицы. Диаграммы. Столбчатые диаграммы, чтение и построение диаграмм. Круговые диаграммы, чтение круговых диаграмм. Представление данных в виде таблиц, диаграмм. Примеры опросов общественного мнения. Сбор и представление информации.
Понятие о случайном опыте и событии. Достоверное и невозможное события. Комбинаторные задачи. Примеры решения комбинаторных задач перебором вариантов.
Множество, элемент множества. Задание множеств перечислением элементов, характеристическим свойством. Стандартные обозначения числовых множеств. Пустое множество и его обозначение. Подмножество. Иллюстрация отношений между множествами с помощью диаграмм Эйлера-Венна. Понятие о классификации. Теоретико-множественные модели некоторых комбинаторных задач.
Наглядная геометрия (45 ч.)
Разнообразный вид линий. Виды линий. Внутренняя и внешняя области. Наглядное представление о фигурах на плоскости. Прямая. Части прямой. Луч. Отрезок. Ломаная. Длина линий. Как сравнить два отрезка. Единицы длины. Длина отрезка. Длина ломаной. Как измерить длину кривой. Как обозначаются и сравниваются углы. Угол. Биссектриса угла. Виды углов. Величины. Как измерить величину угла. Построение угла заданной величины. Многоугольники. Периметр многоугольника. Треугольники и их виды. Классификация треугольников по сторонам. Равнобедренный треугольник. Классификация треугольников по углам. Прямоугольник. Квадрат. Построение прямоугольника. Периметр прямоугольника. Диагонали прямоугольника. Геометрические тела. Многогранники. Изображение пространственных тел. Параллелепипед, куб. Пирамида. Единицы объёма. Объём прямоугольного параллелепипеда. Что такое развертка. Вертикальные углы. Перпендикулярные прямые. Параллельные прямые. Прямые в пространстве. Расстояние между двумя точками. Расстояние от точки до фигуры. Расстояние между параллельными прямыми. Расстояние от точки до плоскости. Взаимное расположение прямой и окружности. Построение касательной. Две окружности. Неравенство треугольника. Построение треугольников по трём сторонам. Цилиндр, конус, шар. Сечение. Точка, симметричная относительно прямой. Симметрия и равенство. Симметрия в пространстве. Зеркальная симметрия. Симметрия фигур. Прямоугольник, равнобедренный треугольник, окружность. Симметрия относительно точки. Центр симметрии фигуры. Задачи на разрезание и составление фигур. Геометрия на клетчатой бумаге. Параллелограмм. Свойства параллелограмма. Виды параллелограммов. Какой многоугольник называется правильным. Окружность и правильный многоугольник. Правильные многогранники. Площадь параллелограмма и треугольника. Призма. Параллелепипед. Развертка призмы.
Резерв 20 часов.
7-9 класс Математика (АЛГЕБРА) (всего 306ч)
Действительные числа (15 ч.)
Расширение множества натуральных чисел до множества целых чисел, множества целых чисел до множества рациональных чисел. Понятие об иррациональном числе. Иррациональность числа и несоизмеримость стороны и диагонали квадрата. Десятичные приближения иррациональных чисел. Множество действительных чисел; представление действительных чисел в виде бесконечных десятичных дробей. Сравнение действительных чисел. Взаимно однозначное соответствие между действительными числами и точками координатной прямой. Числовые промежутки, интервал, отрезок, луч. Изображение чисел точками координатной прямой. Квадратный корень из числа. Корень третьей степени. Запись корней с помощью степени с дробным показателем.
Степень с целым показателем. Свойства степени с целым показателем. Преобразование выражений со степенями.
Алгебраические выражения ( 90 ч.)
Алгебраические выражения. Числовые выражения. Буквенные выражения (выражения с переменными). Числовое значение буквенного выражения. Сравнение значений выражений. Допустимые значения переменных, входящих в алгебраические выражения. Подстановка выражений вместо переменных.
Преобразование буквенных выражений на основе свойств арифметических действий. Равенство буквенных выражений. Тождество. Доказательство тождеств. Тождественные преобразования выражений.
Степень с натуральным показателем. Умножение степеней. Деление степеней. Возведение в степень произведения и степени. Одночлен и его стандартный вид. Умножение одночленов, возведение одночленов в степень.
Многочлен и его стандартный вид. Степень многочлена. Сложение, вычитание, умножение многочлена на одночлен. Вынесение общего множителя за скобки. Умножение многочленов. Разложение многочлена на множители способом группировки.
Возведение в квадрат суммы и разности двух выражений. Возведение в куб суммы и разности двух выражений. Формула разности квадратов. Преобразование целого выражения в многочлен. Разложение многочленов на множители. Многочлены с одной переменной. Корень многочлена. Возведение двучлена в степень.
Алгебраическая дробь. Основное свойство алгебраической дроби. Сложение, вычитание, умножение, деление алгебраических дробей. Рациональные выражения и их преобразования. Доказательство тождеств. Квадратные корни. Свойства арифметических квадратных корней и их применение к преобразованию числовых выражений и вычислениям( корень из произведения, частного, степени).
Квадратный трехчлен. Теорема о разложении квадратного трехчлена множители, разложение квадратного трехчлена на множители.
Уравнения (65 ч.)
Уравнение с одной переменной. Корень уравнения. Свойства числовых равенств. Равносильность уравнений.
Линейное уравнение с одной переменной. Решение задач с помощью уравнения.
Линейное уравнение с двумя переменными. График линейного уравнения с двумя переменными. Корни уравнения. Система уравнений с двумя переменными. Равносильность систем. Системы двух линейных уравнений с двумя переменными; решение подстановкой и сложением. Решение текстовых задач алгебраическим способом. Квадратное уравнение: формула корней квадратного уравнения. Неполные квадратные уравнения. Теорема Виета. Биквадратные уравнения. Решение уравнений, сводящихся к линейным и квадратным. Решение дробно-рациональных уравнений. Решение текстовых задач алгебраическим способом. Целое уравнение и его корни. Примеры решения уравнений третьей и четвертой степени разложением на множители. Дробные рациональные уравнения. Решение текстовых задач алгебраическим способом.
Уравнение с двумя переменными. Линейное уравнение с двумя переменными, примеры решения уравнений в целых числах. Примеры решения систем нелинейных уравнений с двумя переменными.
Декартовы координаты на плоскости. Графическая интерпретация уравнения с двумя переменными. График линейного уравнения с двумя переменными; угловой коэффициент прямой; условие параллельности прямых. Графики простейших нелинейных уравнений: парабола, гипербола, окружность. Графическая интерпретация систем уравнений с двумя переменными. Способ подстановки.
Неравенства (20 ч.)
Числовые неравенства и их свойства. Числовые промежутки. Координатная прямая.
Неравенство с одной переменной. Равносильность неравенств. Линейные неравенства с одной переменной. Системы неравенств с одной переменной.
Неравенства второй степени с одной переменной. Квадратные неравенства. Примеры решения дробно-рациональных неравенств. Метод интервалов.
Неравенства с двумя переменными. Системы неравенств с двумя переменными. Графическая интерпретация неравенств и систем неравенств с двумя переменными.
Измерения, приближения, оценки. (10 ч.)
Приближенное значение величины, точность приближения. Запись приближенных значений. Действия над приближенными значениями. Вычисления с приближенными данными на калькуляторе. Размеры объектов окружающего мира (от элементарных частиц до Вселенной), длительность процессов в окружающем мире. Выделение множителя - степени 10 в записи числа. Стандартный вид числа. Прикидка и оценка результатов вычислений
Зависимости между величинами (13 ч.)
Зависимость между величинами. Представление зависимостей между величинами в виде формул. Вычисления по формулам. Прямая пропорциональная зависимость: задание формулой, коэффициент пропорциональности; свойства. Примеры прямо пропорциональных зависимостей. Решение задач на прямую пропорциональную зависимость.
Обратная пропорциональная зависимость: задание формулой, коэффициент обратной пропорциональности; свойства. Примеры обратных пропорциональных зависимостей. Свойства функций, их отображение на графике. Примеры графиков зависимостей, отражающих реальные процессы. Решение задач на обратную пропорциональную зависимость.
Числовые функции (25 ч.)
Понятие функции. Область определения и множество значений функции Функции, описывающие прямую пропорциональную зависимость, ее график и свойства. Прямая пропорциональность, ее график и свойства. Линейная функция, ее график и свойства. Построение графиков прямой пропорциональности, линейной функции. Задание функции несколькими способами.
Функции у = х2, у=х3, их графики.
Функция, описывающая обратную пропорциональную зависимость, ее график и свойства.
Функция у=√х, ее график и свойства.
Способы задания функции. График функции. Свойства функции, их отображение на графике: возрастание и убывание функции, нули функции, сохранение знака. Чтение и построение графиков функций.
Примеры графиков, отражающих реальные процессы. Квадратичная функция, ее график и свойства. Степенные функции с натуральными показателями 2 и 3, их графики и свойства.
Числовые последовательности (15 ч.)
Понятие числовой последовательности. Задание последовательности рекуррентной формулой и формулой n-го члена. Арифметическая и геометрическая прогрессии. Формулы n-го члена арифметической и геометрической прогрессий, суммы первых п членов. Изображение членов арифметической и геометрической прогрессий точками координатной плоскости. Линейный и экспоненциальный рост. Сложные проценты.
Описательная статистика (5 ч.)
Представление данных в виде таблиц, диаграмм, графиков. Случайная изменчивость. Статистические характеристики набора данных: среднее арифметическое, медиана, наибольшее и наименьшее значения,
размах, дисперсия. Репрезентативные и нерепрезентативные выборки.
Случайные события и вероятность (5 ч.)
Понятие о случайном опыте и случайном событии. Элементарные события. Частота случайного события. Статистический подход к понятию вероятности. Несовместные события. Формула сложения вероятностей. Вероятности противоположных событий. Независимые события. Умножение вероятностей. Достоверные и невозможные события. Равновозможность событий. Классическое определение вероятности
Элементы комбинаторики и теории вероятностей (8 ч.)
Решение комбинаторных задач перебором вариантов. Комбинаторное правило умножения. Перестановки и факториал. Относительная частота и вероятность случайного события. Сложение и умножение вероятностей.
Множества. Элементы логики (5 ч.)
Определение. Аксиомы и теоремы. Доказательство. Доказательство от противного. Теорема, обратная данной. Пример и контрпример. Иллюстрация отношений между множествами с помощью диаграмм Эйлера-Венна. Понятие о равносильности, следовании, употребление логических связок если ..., то ..., в том и только том случае. Логические связки и, или
Резерв 30 часов.
7-9 класс Математика (ГЕОМЕТРИЯ) (всего 204ч)
Геометрические фигуры (102 ч.)
Прямые и углы. Точка, прямая, плоскость. Отрезок, луч. Угол. Прямой угол, острый и тупой углы, развернутый угол. Вертикальные и смежные углы. Биссектриса угла и ее свойства. Свойства углов с параллельными и перпендикулярными сторонами. Перпендикулярные прямые.
Треугольник. Прямоугольные, остроугольные, тупоугольные треугольники. Первый признак равенства треугольников. Решение задач на применение первого признака равенства треугольников. Высота, медиана, биссектриса. Равнобедренные и равносторонние треугольники. Свойства и признаки равнобедренного треугольника. Второй признак равенства треугольников. Решение задач на применение второго признака равенства треугольников. Третий признак равенства треугольников. Решение задач на применение третьего признака равенства треугольников.
Параллельные и пересекающиеся прямые. Определение параллельных прямых. Признаки и свойства параллельности прямых. Теоремы об углах, образованных двумя параллельными прямыми и секущей. Теорема Фалеса. Сумма углов треугольника Соотношения между сторонами и углами треугольника. Внешние углы треугольника. Неравенство треугольника. Прямоугольные треугольники и их свойства. Признаки равенства прямоугольных треугольников. Перпендикуляр и наклонная к прямой.
Многоугольник. Выпуклые многоугольники. Сумма углов выпуклого многоугольника.
Четырехугольник. Параллелограмм, его свойства и признаки. Прямоугольник, его свойства и признаки. Квадрат, его свойства и признаки. Ромб, его свойства и признаки. Трапеция, средняя линия трапеции.
Теорема Пифагора. Теорема, обратная теореме Пифагора.
Подобие треугольников. Признаки подобия треугольников. средняя линия треугольника Пропорциональные отрезки в прямоугольном треугольнике. Синус, косинус, тангенс, котангенс острого угла прямоугольного треугольника.
Окружность и круг. Дуга, хорда. Сектор, сегмент. Центральный угол, вписанный угол; величина вписанного угла. Взаимное расположение прямой и окружности, двух окружностей. Касательная и секущая к окружности, их свойства. Серединный перпендикуляр к отрезку. Геометрическое место точек. Свойства биссектрисы угла и серединного перпендикуляра к отрезку. Решение задач на вычисление, доказательство с использованием свойств изученных фигур.
Правильные многоугольники. Вписанные и описанные многоугольники. Окружность, вписанная в треугольник, и окружность, описанная около треугольника. Вписанные и описанные окружности правильного многоугольника.
Наглядные представления о пространственных телах. Куб, параллелепипед, призма, пирамида, шар, сфера, конус, цилиндр. Примеры сечений. Примеры разверток.
Измерение геометрических величин (35 ч.)
Измерение отрезков. Длина ломаной. Измерение углов.
Расстояние от точки до прямой. Расстояние между параллельными прямыми.
Понятие площади плоских фигур. Равносоставленные и равновеликие фигуры. Площадь прямоугольника. Площади параллелограмма, треугольника и трапеции. Соотношение между площадями подобных фигур.
Решение задач на вычисление и доказательство с использованием изученных формул.
Решение прямоугольных треугольников. Синус, косинус, тангенс, котангенс острого угла прямоугольного треугольника. и углов от 0 до 180°; приведение к острому углу Основное тригонометрическое тождество. Формулы, связывающие синус, косинус, тангенс, котангенс одного и того же угла. Решение треугольников: теорема косинусов и теорема синусов. Замечательные точки треугольника.
Формулы, выражающие площадь треугольника: через две стороны и угол между ними.
Периметр многоугольника. Длина окружности, число пи; длина дуги окружности.
Градусная мера угла, соответствие между величиной центрального угла и длиной дуги окружности.
Площадь правильного многоугольника. Формулы, выражающие площадь треугольника: через периметр и радиус вписанной окружности, формула Герона. Площадь круга и площадь сектора.
Связь между площадями подобных фигур. Объем тела.
Формулы объема прямоугольного параллелепипеда, куба, шара, цилиндра и конуса.
Построения с помощью циркуля и линейки (17 ч.)
Деление отрезка на п равных частей. Построение угла, равного данному. Построение биссектрисы угла. Построение перпендикуляра к прямой. Деление отрезка пополам. Практические способы построения параллельных прямых. Основные задачи на построение треугольников. Построение треугольника по трем элементам.
Построение серединного перпендикуляра к отрезку.
Геометрические преобразования (10 ч.)
Понятие о равенстве фигур. Понятие о движении: осевая и центральная симметрии.
Понятие о движении. Параллельный перенос, поворот. Понятие о подобии фигур и гомотетии.
Векторы (10 ч.)
Длина (модуль) вектора. Равенство векторов. Коллинеарные векторы. Координаты вектора. Умножение вектора на число, сумма векторов, разложение вектора по двум неколлинеарным векторам. Скалярное произведение векторов.
Координаты (10 ч.) Разложение вектора по двум неколлинеарным векторам. Координаты вектора. Связь между координатами вектора и координатами его начала и конца. Координаты середины отрезка. Вычисление длины вектора. Формула расстояния между двумя точками плоскости. Уравнение линии на плоскости. Уравнение прямой. Уравнение окружности.
Резерв 20 часов.
МАТЕМАТИКА В ИСТОРИЧЕСКОМ РАЗВИТИИ
История формирования понятия числа: натуральные числа, дроби, недостаточность рациональных чисел для геометрических измерений, иррациональные числа. Старинные системы записи чисел. Дроби в Вавилоне, Египте, Риме. Открытие десятичных дробей. Старинные системы мер. Десятичные дроби и метрическая система мер. Появление отрицательных чисел и нуля. Л. Магницкий. Л. Эйлер.
Зарождение алгебры в недрах арифметики. Ал-Хорезми. Рождение буквенной символики. П. Ферма, Ф. Виет, Р. Декарт. История вопроса о нахождении формул корней алгебраических уравнений, неразрешимость в радикалах уравнений степени, большей четырех. Н. Тарталья, Дж. Кардано, Н. X. Абель, Э. Галуа.
Изобретение метода координат, позволяющего переводить геометрические объекты на язык алгебры. Р. Декарт и П. Ферма. Примеры различных систем координат на плоскости.
Задача Леонардо Пизанского (Фибоначчи) о кроликах, числа Фибоначчи. Задача о шахматной доске.
Истоки теории вероятностей: страховое дело, азартные игры. П. Ферма и Б. Паскаль. Я. Бернулли. А. Н. Колмогоров.
От землемерия к геометрии. Пифагор и его школа. Фалес. Архимед. Построение правильных многоугольников.
Повторение и итоговый контроль.
VI. Тематическое планирование и виды деятельности учащихся.
| Содержание учебного предмета, курса | Характеристика деятельности обучающихся
|
| Натуральные числа (50 часов) |
| 5 класс. Натуральные числа ( 50 часов) Натуральные числа (3ч) 1)Как записывают и читают числа. 2)Римская нумерация. 3)Десятичная нумерация. Натуральный ряд. Действия с натуральными числами. (21ч) 1)Арифметические действия с натуральными числами. 2)Сложение натуральных чисел. 3)Свойства нуля при сложении. 4)Вычитание натуральных чисел как действие, обратного сложению. 5)Свойства нуля при вычитании. 6)Прикидка и оценка суммы. 7)Умножение натуральных чисел. 8)Свойства нуля и единицы при умножении. 9)Деление натуральных чисел как действие, обратное умножению. 10)Свойства нуля и единицы при делении. 11)Числовые выражения. 12)Вычисление значений числовых выражений. 13)Порядок действий в числовых выражениях. 14)Использование скобок. 15)Составление и запись числовых выражений. 16) Степень числа. 17)Возведение натурального числа в степень. 18)Квадрат и куб числа. 19) Вычисление значений выражений, содержащих степень. 20) Решение текстовых задач арифметическим способом. 21) Контрольная работа. Использование свойств действий при вычислениях (10ч) 1)Свойства сложения. 2)Свойства умножения. 3)Переместительное свойство. 4)Сочетательное свойства. 5)Удобные вычисления. 6)Распределительное свойство умножения относительно сложения. 7) Примеры вычислений с использованием распределительного свойства. 8) Решение задач на части. 9) Задачи на уравнивание. 10) Контрольная работа. Делимость чисел. (16ч) 1)Делители числа. 2)Кратные числа. 3)Простые числа. 4)Составные числа и число 1. 5)Решето Эратосфена. 6)Разложение натурального числа на простые множители. 7)Наибольший общий делитель. 8)Наименьшее общее кратное. 9)Свойства делимости. 10)Делимость произведения. 11)Делимость суммы. Контрпример. 12)Признаки делимости на 10, на 5, на 2. 13) Признаки делимости на 9 и на 3. 14) Деление с остатком. 15) Примеры деления чисел с остатком 16) Контрольная работа. |
Описывать свойства натурального ряда. Читать и записывать натуральные числа, сравнивать и упорядочивать их. Выполнять вычисления с натуральными числами; вычислять значения степеней. Формулировать свойства арифметических действий, записывать их с помощью букв, преобразовывать на их основе числовые выражения. Анализировать и осмысливать текст задачи, переформулировать условие, извлекать необходимую информацию, моделировать условие с помощью схем, рисунков, реальных предметов; строить логическую цепочку рассуждений; критически оценивать полученный ответ, осуществлять самоконтроль, проверяя ответ на соответствие условию. Формулировать определения делителя и кратного, простого числа и составного числа, свойства и признаки делимости. Доказывать и опровергать с помощью контрпримеров утверждения о делимости чисел. Классифицировать натуральные числа (четные и нечетные, по остаткам от деления на 3 и т. п.). Исследовать простейшие числовые закономерности, проводить числовые эксперименты ( в том числе с использованием калькулятора, компьютера)
|
| Дроби (120 часов) |
| 5 класс. Дроби (54 часа) Дроби. (19ч) 1)Деление целого на доли. 2)Обыкновенные дроби. 3)Правильные и неправильные дроби. 4)Изображение дробей точками на координатной прямой. 5)Основное свойство дроби. 6)Равные дроби. 7)Приведение дроби к новому знаменателю. 8) - 9) Сокращение дробей. 10) Сравнение дробей с одинаковыми знаменателями. 11) - 12) Приведение дробей к общему знаменателю. 13) - 14) Сравнение дробей с разными знаменателями. 15) Некоторые другие приемы сравнения дробей. 16) Деление и дроби. 17)- 18)Представление натуральных чисел дробями. 19) Контрольная работа. Действия с дробями. (35ч) 1)Сложение дробей с одинаковыми знаменателями. 2) Вычитание дробей с одинаковыми знаменателями. 3)Сложение дробей с разными знаменателями. 4)Вычитание дробей с разными знаменателями. 5)-6)Смешанная дробь. 7) Выделение целой части из неправильной дроби. 8)Представление смешанной дроби в виде неправильной. 9)Сложение смешанных дробей 10)-11)Вычитание смешанных дробей. 12) Правило умножения дробей. 13) -14) Умножение дроби на натуральное число. 15) -16) Умножение дроби на смешанную дробь. 17) -18) Взаимообратные дроби. 19)-20)Правило деления дробей. 21) – 22)Правило деления дробей на натуральное число. 23) –24) Разные действия с дробями. 25) – 26) Нахождение части от целого. 27) – 28) Нахождение целого по его части. 29) -30) Задачи на совместную работу. 31)-32) Задачи на движение. 33)-34) Обобщающий урок по теме «Дроби». 35) Контрольная работа по теме «Дроби». 6 класс. Дроби (66 часов) Дроби и проценты. (20ч) Дробь, числитель и знаменатель дроби. Основное свойство дроби. Приведение дроби к новому знаменателю. Сокращение дробей. -6) Правила действий с дробями: сложение, вычитание, умножение, деление дробей. 7)Задачи на совместную работу. 8)«Многоэтажные» дроби. 9) – 10) Нахождение части от числа. 11) -12)Нахождение числа по его части. 13)Какую часть одно число составляет от другого. 14) Понятие процента. 15)-16) Решение задач на нахождение процента от величины, на увеличение величины на несколько процентов. 17)Особенности представления данных на столбчатых и круговых диаграммах. 18)Построение диаграмм. 19) Обобщающий урок по теме «Дроби и проценты». 20) Контрольная работа по теме «Дроби и проценты». Десятичные дроби. (9ч) 1)Десятичная запись чисел. 2) Представление десятичной дроби в виде обыкновенной и обыкновенной в виде десятичной. 3) Изображение десятичных дробей точками на координатной прямой. 4) Десятичные дроби и метрическая система мер. 5) Признак обратимости обыкновенной дроби в десятичную. Десятичные представления некоторых обыкновенных дробей. 6) Выражение величин дробями. Равные десятичные дроби. 7) Сравнение и упорядочивание десятичных дробей. Сравнение обыкновенной дроби и десятичной. 8) Обобщающий урок по теме «Десятичные дроби» 9) Контрольная работа по теме «Десятичные дроби» Действия с десятичными дробями. (27ч) 1)-2)Сложение десятичных дробей. 3)-4)Вычитание десятичных дробей. 5)-6)Действия с обыкновенными и десятичными дробями. Решение задач. 7)Умножение десятичной дроби на единицу с нулями. 8)-9)Деление десятичной дроби на единицу с нулями. 10)Переход от одних единиц измерения к другим. 11)-12)Умножение десятичной дроби на натуральное число. 13)-14)Умножение десятичной дроби на десятичную дробь. 15) Возведение десятичной дроби в квадрат и куб. 16)Умножение десятичной дроби на обыкновенную. 17)Разные действия с десятичными дробями. Решение задач. 18)Деление десятичной дроби на натуральное число. 19)-20)Деление на десятичную дробь. 21)Пропорция. Основное свойство пропорции. 22)Вычисление частного десятичных дробей в общем случае. 23)Решение задач на движении. 24)Что значит округлить десятичную дробь. Правило округления десятичных дробей. 25)Приближённое частное. 26) Обобщающий урок по теме «Действия с десятичными дробями» 27)Контрольная работа по теме «Действия с десятичными дробями» Отношения и проценты. (10ч) 1) Отношение двух чисел. 2)Деление в данном отношении. 3)Решение задач на деление в данном отношении. 4)Выражение отношения в процентах. 5)Масштаб. 6)Представление процента десятичной дробью. 7)Выражение дроби в процентах. 8)Нахождение процентов от величины. 9)Нахождение величины по её проценту. 10)Решение текстовых задач арифметическими способами.
|
Моделировать в графической, предметной форме понятия и свойства, связанные с понятием обыкновенной дроби. Формулировать, записывать с помощью букв основное свойство обыкновенной дроби, правила действий с обыкновенными дробями. Преобразовывать обыкновенные дроби, сравнивать и упорядочивать их. Выполнять вычисления с обыкновенными дробями. Записывать и читать десятичные дроби. Представлять обыкновенные дроби в виде десятичных и десятичные в виде обыкновенных; находить десятичные приближения обыкновенных дробей. Сравнивать и упорядочивать десятичные дроби. Выполнять вычисления с десятичными дробями. Использовать эквивалентные представления дробных чисел при их сравнении, при вычислениях. Выполнять прикидку и оценку в ходе вычислений. Объяснять, что такое процент. Представлять проценты в дробях и дроби в процентах. Осуществлять поиск информации (в СМИ), содержащей данные, выраженные в процентах, интерпретировать их. Приводить примеры использования отношений в практике. Решать задачи на проценты и дроби (в том числе задачи из реальной практики, используя при необходимости калькулятор), использовать понятия отношения и пропорции при решении задач. Анализировать и осмысливать текст задачи, переформулировать условие, извлекать необходимую информацию, моделировать условие с помощью схем, рисунков, реальных предметов; строить логическую цепочку рассуждений; критически оценивать полученный ответ, осуществлять самоконтроль, проверяя ответ на соответствие условию. Проводить несложные исследования, связанные со свойствами дробных чисел, опираясь на числовые эксперименты (в том числе с использованием калькулятора, компьютера)
Моделировать в графической и предметной форме обыкновенные дроби, вычисления с дробями. Использовать дробную черту как знак деления при записи нового вида дробного выражения («многоэтажная» дробь). Применять различные способы вычисления значений таких выражений, выполнять преобразования «многоэтажных» дробей. Решать задачи на совместную работу. Анализировать числовые закономерности, связанные с арифметическими действий с обыкновенными дробями, доказывать в несложных случаях выявленные свойства. Моделировать понятие процента в графической форме. Решать задачи на нахождение нескольких процентов величины, на увеличение (уменьшение) величины на несколько процентов.
|
| Рациональные числа(40 часов) |
| 6 класс. Рациональные числа (40часов) Целые числа(13часов) 1)Числа, противоположные натуральным. Множество целых чисел. Ряд целых чисел. 2)Изображение целых чисел точками на координатной прямой. Сравнение и упорядочивание целых чисел. 3)Сложение целых чисел одного знака, разных знаков. 4)Сумма противоположных чисел. 5)Вычисление суммы нескольких целых чисел. Вычисление числовых значений буквенных выражений. 6)Правило нахождения разности двух целых чисел. 7)Вычисление значений выражений, содержащих только действия сложения и вычитания. 8) Вычисление значений буквенных выражений. 9)Умножение целых чисел. 10)Деление целых чисел. 11)Разные действия с целыми числами. 12)Обобщающий урок по теме «Целые числа» 13) Контрольная работа по теме «Целые числа» Рациональные числа. (20ч) 1)Рациональные числа: положительные и отрицательные числа (целые и дробные); противоположные числа. 2)Множество рациональных чисел. 3)Изображение рациональных чисел точками координатной прямой. 4)Сравнение рациональных чисел с помощью координатной прямой. 5)Установление отношений «больше» («меньше») между рациональными числами. 6)Понятие модуля числа. 7)Арифметические действия с рациональными числами. 8)-9)Правила сложения рациональных чисел одного знака, разных знаков. 10)-11)Свойства арифметических действий. Свойства сложения, свойство нуля при сложении. 12)-13)Вычитание рациональных чисел. 14)-15)Умножение и деление рациональных чисел, правила знаков при умножении и делении. 16)Свойства умножения, свойства 0, 1 и -1 при умножении. 17)-18)Равенство 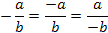 и его применение при вычислениях. и его применение при вычислениях. 19) Обобщающий урок по теме «Рациональные числа» 20) Контрольная работа по теме «Рациональные числа». Отношения и проценты. (7ч) 1) Увеличение величины на несколько процентов. 2) Уменьшение величины на несколько процентов.
3)Увеличение и уменьшение величины на несколько процентов. 4)Округление и прикидка. 5)Нахождение процентного отношения. Решение текстовых задач. 6) Обобщающий урок по теме «Отношения и проценты». 7) Контрольная работа по теме «Отношения и проценты» |
Приводить примеры использования в окружающем мире положительных и отрицательных чисел (температура, выигрыш — проигрыш, выше — ниже уровня моря и т. п.). Изображать точками координатной прямой положительные и отрицательные рациональные числа. Характеризовать множество целых чисел, множество рациональных чисел. Формулировать и записывать с помощью букв свойства действий с рациональными числами, применять для преобразования числовых выражений. Сравнивать и упорядочивать рациональные числа, выполнять вычисления с рациональными числами |
| Измерения, приближения, оценки. Зависимости между величинами ( 30 часов) |
| 5класс. Измерения, приближения, оценки. Зависимости между величинами ( 20 часов) Натуральные числа (6 часов) 1)Округление натуральных чисел. 2)Единицы измерения длины, массы, времени, скорости. Примеры зависимостей между величинами: скорость, время, расстояние; производительность, время, работа; цена, количество, стоимость. 3)Представление зависимостей в виде формул. Вычисления по формулам. 3)Движения в противоположных направлениях, скорость сближения, скорость удаления. 4)-5)Движение по реке, скорость движения по течению, против течения. 6)Решение текстовых задач арифметическими способами. Линии (3 часа) 1)Окружность и круг. 2)-3)Радиус и диаметр окружности. Углы и многоугольники (3 часа) 1)Диагональ многоугольника. 2)-3)Выпуклые многоугольники. Треугольники и четырехугольники (5 часов) 1)Равные фигуры. Признаки равенства. 2)Единицы измерения площадей. 3)Площадь фигуры. 4)Площадь прямоугольника. 5)Площадь арены цирка. Многогранники (3 часа) 1)Развёртка прямоугольного параллелепипеда и пирамиды. 2)Объем прямоугольного параллелепипеда. 3)Единицы измерения объема.
8 класс. Измерения. Приближения. Оценки. (10 часов) 1)Приближенное значение величины, точность приближения. 2)Запись приближенных значений. 3)Действия над приближенными значениями. 4)Вычисления с приближенными данными на калькуляторе. 5)Размеры объектов окружающего мира (от элементарных частиц до Вселенной), длительность процессов в окружающем мире. 6)Выделение множителя - степени 10 в записи числа. 7)-8)Стандартный вид числа. 9)-10) Прикидка и оценка результатов вычислений
|
Выражать одни единицы измерения величины в других единицах (метры в километрах, минуты в часах и т. п.). Округлять натуральные числа и десятичные дроби. Выполнять прикидку и оценку в ходе вычислений. Моделировать несложные зависимости с помощью формул; выполнять вычисления по формулам. Использовать знания о зависимостях между величинами (скорость, время, расстояние; работа, производительность, время и т. п.) при решении текстовых задач.
Находить, анализировать, сопоставлять числовые характеристики объектов окружающего мира. Использовать запись чисел в стандартном виде для выражения размеров объектов, длительности процессов в окружающем мире. Сравнивать числа и величины, записанные с использованием степени 10. Использовать разные формы записи приближенных значений; делать выводы о точности приближения по их записи. Выполнять вычисления с реальными данными. Выполнять прикидку и оценку результатов вычислений |
| Элементы алгебры (25 часов) |
| 6 класс. Элементы алгебры (25ч.) Выражения. Формулы. Уравнения. (25ч) 1)Математические выражения. 2) Использование букв для обозначения чисел; для записи свойств арифметических действий 3) Буквенные выражения. Математические предложения. 4)Числовое значение буквенного выражения. 5)Допустимые выражения букв в выражении 6) Составление выражения по условию задачи с буквенными данными. 7) Некоторые геометрические формулы. 8)Формула стоимости. Формула пути. 9) Число π. Формула длины окружности. 10) Формула площади круга. 11) Вычисление размеров фигур, ограниченных окружностями и их дугами. 12) Формула объёма шара. Вычисления, связанные с цилиндром и шаром. 13) Контрольная работа по теме «Выражения, формулы, уравнения» 14) Уравнение, корень уравнения. 15)Решение уравнений. 16)-17) Нахождение неизвестных компонентов арифметических действий. 18)-19) Решение задач с помощью уравнений. 20) Примеры различных систем координат в окружающем мире. Декартовы координаты на плоскости. 21) Прямоугольная система координат на плоскости, Координаты точки. 22)Построение точки по ее координатам. 23)Определение координат точки на плоскости. 24) Обобщающий урок по теме «Выражения, формулы, уравнения» 25) Контрольная работа по теме «Выражения. Формулы. Уравнения»
|
Читать и записывать буквенные выражения, составлять буквенные выражения по условиям задач. Вычислять числовое значение буквенного выражения при заданных значениях букв. Составлять уравнения по условиям задач. Решать простейшие уравнения на основе зависимостей между компонентами арифметических действий. Строить на координатной плоскости точки и фигуры по заданным координатам; определять координаты точек |
| Описательная статистика. Вероятность. Комбинаторика. Множества (20 часов) |
| 5 класс. Описательная статистика. Вероятность. Комбинаторика. Множества (12 часов) Таблицы и диаграммы ( 9 часов) 1)Как устроены таблицы. 2)Чтение таблиц. 3)Как составлять таблицы. 4) Диаграммы. 5)Столбчатые диаграммы, чтение и построение диаграмм. 6)Круговые диаграммы, чтение круговых диаграмм. 7)Представление данных в виде таблиц, диаграмм. 8)Примеры опросов общественного мнения. 9)Сбор и представление информации. Натуральные числа. (3 часа) 1)Понятие о случайном опыте и событии. Достоверное и невозможное события. 2)Комбинаторные задачи. 3)Примеры решения комбинаторных задач перебором вариантов. 6 класс. Описательная статистика. Вероятность. Комбинаторика. Множества. (8 часов) Множества. Комбинаторика. (8ч) 1)Множество, элемент множества. 2)-3) Задание множеств перечислением элементов, характеристическим свойством. 4)Стандартные обозначения числовых множеств. 5)Пустое множество и его обозначение. Подмножество. 6)Иллюстрация отношений между множествами с помощью диаграмм Эйлера-Венна. 7)Понятие о классификации. 8)Теоретико-множественные модели некоторых комбинаторных задач.
|
Извлекать информацию из таблиц и диаграмм, выполнять вычисления по табличным данным, сравнивать величины, находить наибольшие и наименьшие значения и др. Выполнять сбор информации в несложных случаях, организовывать информацию в виде таблиц и диаграмм, в том числе с помощью компьютерных программ. Приводить примеры случайных событий, достоверных и невозможных событий. Сравнивать шансы наступления событий; строить речевые конструкции с использованием словосочетаний более вероятно, маловероятно и др. Выполнять перебор всех возможных вариантов для пересчета объектов или комбинаций, выделять комбинации, отвечающие заданным условиям.
Приводить примеры конечных и бесконечных множеств. Находить объединение и пересечение конкретных множеств. Приводить примеры несложных классификаций из различных областей жизни. Иллюстрировать теоретико-множественные понятия с помощью кругов Эйлера |
| Наглядная геометрия (45 часов) |
|
5 класс. Наглядная геометрия ( 25 часов) Линии.(6ч) 1)Разнообразный вид линий. 2)Виды линий. Внутренняя и внешняя области. 3)Наглядное представление о фигурах на плоскости. Прямая. Части прямой. Луч. Отрезок. Ломаная. 4) Длина линий. Как сравнить два отрезка. 5)Единицы длины. Длина отрезка. 6)Длина ломаной. Как измерить длину кривой. Углы и многоугольники. (6ч) 1)Как обозначаются и сравниваются углы. 2)Угол. Биссектриса угла. Виды углов. 3)Величины. 4)Как измерить величину угла. 5)Построение угла заданной величины. 6) Многоугольники. Периметр многоугольника. Треугольники и четырехугольники. (5ч) 1)Треугольники и их виды. 2)Классификация треугольников по сторонам. Равнобедренный треугольник. 3)Классификация треугольников по углам. 4)Прямоугольник. Квадрат. Построение прямоугольника. 5)Периметр прямоугольника. Диагонали прямоугольника. Многогранники. (8ч) 1)Наглядные представления о пространственных фигурах. 2)Геометрические тела. 3)Многогранники. 4)Изображение пространственных тел. 5)Параллелепипед, куб. 6)Пирамида. 7)Объём прямоугольного параллелепипеда. Единицы объёма. 8)Что такое развертка. 6 класс. Наглядная геометрия ( 20 часов) Прямые на плоскости и в пространстве. (5ч) 1)Вертикальные углы. Перпендикулярные прямые. 2) Параллельные прямые. Прямые в пространстве. 3) Расстояние между двумя точками, Расстояние от точки до фигуры. 4) Расстояние между параллельными прямыми. Расстояние от точки до плоскости. 5) Контрольная работа по теме «Прямые на плоскости и в пространстве» Окружность. (5ч) 1)Взаимное расположение прямой и окружности. Построение касательной. 2) Две окружности 3)Неравенство треугольника. Построение треугольников по трём сторонам 4) Цилиндр, конус, шар. Сечение. 5) Контрольная работа по теме «Окружность». Симметрия. (5ч) 1)Точка, симметричная относительно прямой. Симметрия и равенство. 2)Симметрия в пространстве. Зеркальная симметрия. 3) Симметрия фигур. Прямоугольник, равнобедренный треугольник, окружность. 4) Симметрия относительно точки. Центр симметрии фигуры. 5)Задачи на разрезание и составление фигур. Геометрия на клетчатой бумаге. Многоугольники и многогранники. (5ч) 1)Параллелограмм. Свойства параллелограмма. Виды параллелограммов. 2)Какой многоугольник называется правильным. Окружность и правильный многоугольник. 3)Правильные многогранники. 4) Площадь параллелограмма и треугольника. 5) Призма. Параллелепипед. Развертка призмы.
|
Распознавать на чертежах, рисунках, в окружающем мире геометрические фигуры, конфигурации фигур (плоские и пространственные). Приводить примеры аналогов геометрических фигур в окружающем мире. Изображать геометрические фигуры и их конфигурации от руки и с использованием чертежных инструментов. Изображать геометрические фигуры на клетчатой бумаге. Измерять с помощью инструментов и сравнивать длины отрезков и величины углов. Строить отрезки заданной длины с помощью линейки и циркуля и углы заданной величины с помощью транспортира. Выражать одни страницы измерения длин через другие. Вычислять площади квадратов и прямоугольников, используя формулы площади квадрата и прямоугольника. Выражать одни единицы измерения площади через другие. Изготавливать пространственные фигуры из разверток; распознавать развертки куба, параллелепипеда, пирамиды, цилиндра и конуса. Рассматривать простейшие сечения пространственных фигур, получаемые путем предметного или компьютерного моделирования, определять их вид. Соотносить пространственные фигуры с их проекциями на плоскость. Вычислять объемы куба и прямоугольного параллелепипеда, используя формулы объема куба и прямоугольного параллелепипеда. Выражать одни единицы измерения объема через другие. Исследовать и описывать свойства геометрических фигур (плоских и пространственных), используя эксперимент, наблюдение, измерение, моделирование. Использовать компьютерное моделирование и эксперимент для изучения свойств геометрических объектов. Моделировать геометрические объекты, используя бумагу, пластилин, проволоку и др. Находить в окружающем мире плоские и пространственные симметричные фигуры. Решать задачи на нахождение длин отрезков, периметров многоугольников; градусной меры углов; площадей квадратов и прямоугольников; объемов кубов и прямоугольных параллелепипедов, куба. Выделять в условии задачи данные, необходимые для решения задачи, строить логическую цепочку рассуждений, сопоставлять полученный результат с условием задачи. Изображать равные фигуры; симметричные фигуры. Конструировать орнаменты и паркеты, изображая их от руки, с помощью инструментов, а также используя компьютерные программы. |
| Действительные числа (15ч.) |
| 8 класс. Квадратные корни (9ч.) Расширение множества натуральных чисел до множества целых чисел, множества целых чисел до множества рациональных чисел. Понятие об иррациональном числе. Иррациональность числа и несоизмеримость стороны и диагонали квадрата. Десятичные приближения иррациональных чисел. Множество действительных чисел; представление действительных чисел в виде бесконечных десятичных дробей. Сравнение действительных чисел. Взаимно однозначное соответствие между действительными числами и точками координатной прямой. Числовые промежутки, интервал, отрезок, луч. Изображение чисел точками координатной прямой. Квадратный корень из числа. Корень третьей степени. Запись корней с помощью степени с дробным показателем. Степень с целым показателем (6ч) Степень с целым показателем. Свойства степени с целым показателем. Преобразование выражений со степенями.
| Описывать множество целых чисел, множество рациональных чисел, соотношение между этими множествами. Сравнивать и упорядочивать рациональные числа, выполнять вычисления с рациональными числами, вычислять значения степеней с целым показателем. Формулировать определение квадратного корня из числа. Использовать график функции у = х2 для нахождения квадратных корней. Вычислять точные и приближенные значения корней, используя при необходимости калькулятор; проводить оценку квадратных корней. Формулировать определение корня третьей степени; находить значения кубических корней, при необходимости используя калькулятор. Исследовать свойства квадратного корня, кубического корня, проводя числовые эксперименты с использованием калькулятора, компьютера. Приводить примеры иррациональных чисел; распознавать рациональные и иррациональные числа; изображать числа точками координатной прямой. Находить десятичные приближения рациональных и иррациональных чисел; сравнивать и упорядочивать действительные числа. Описывать множество действительных чисел. Использовать в письменной математической речи обозначения и графические изображения числовых множеств, теоретико-множественную символику |
| Алгебраические выражения. (90ч.) |
| 7 класс. Алгебраические выражения (56 ч.) Выражения, тождества, уравнения (10ч.) Алгебраические выражения. Числовые выражения. Буквенные выражения (выражения с переменными). Числовое значение буквенного выражения. Сравнение значений выражений. Допустимые значения переменных, входящих в алгебраические выражения. Подстановка выражений вместо переменных. Преобразование буквенных выражений на основе свойств арифметических действий. Равенство буквенных выражений. Тождество. Доказательство тождеств. Тождественные преобразования выражений. Контрольная работа по теме « Выражения, тождества, уравнения » Степень с натуральным показателем (12 ч.) Степень с натуральным показателем. Умножение степеней. Деление степеней. Возведение в степень произведения и степени. Одночлен и его стандартный вид. Умножение одночленов, возведение одночленов в степень. Многочлены (17 ч.) Многочлен и его стандартный вид. Степень многочлена. Сложение, вычитание, умножение многочлена на одночлен. Вынесение общего множителя за скобки. Умножение многочленов. Разложение многочлена на множители способом группировки. Формулы сокращенного умножения (17 ч.). Возведение в квадрат суммы и разности двух выражений. Возведение в куб суммы и разности двух выражений. Формула разности квадратов. Преобразование целого выражения в многочлен. Разложение многочленов на множители. Многочлены с одной переменной. Корень многочлена. Возведение двучлена в степень. 8 класс. Алгебраические выражения (30 ч.) Рациональные дроби (21ч.) Алгебраическая дробь. Основное свойство алгебраической дроби. Сложение, вычитание, умножение, деление алгебраических дробей. Рациональные выражения и их преобразования. Доказательство тождеств. Квадратные корни (9ч.) Квадратные корни. Свойства арифметических квадратных корней и их применение к преобразованию числовых выражений и вычислениям (корень из произведения, частного, степени). 9 класс. Алгебраические выражения (4 ч.) Свойства функций. Квадратичная функция. (4 ч.) Квадратный трехчлен. Теорема о разложении квадратного трехчлена множители, разложение квадратного трехчлена на множители.
|
Выполнять элементарные знаково-символические действия: применять буквы для обозначения чисел, для записи общих утверждений; составлять буквенные выражения по условиям, заданным словесно, рисунком или чертежом; преобразовывать алгебраические суммы и произведения (выполнять приведение подобных слагаемых, раскрытие скобок, упрощение произведений). Вычислять числовое значение буквенного выражения; находить область допустимых значений переменных в выражении.
Формулировать, записывать в символической форме и обосновывать свойства степени с натуральным показателем; применять свойства степени для преобразования выражений и вычислений. Выполнять действия с многочленами. Доказывать формулы сокращенного умножения, применять их в преобразованиях выражений и вычислениях. Выполнять разложение многочленов на множители. Распознавать квадратный трехчлен, выяснять возможность разложения на множители, представлять квадратный трехчлен в виде произведения линейных множителей. Применять различные формы самоконтроля при выполнении преобразований. Формулировать основное свойство алгебраической дроби и применять его для преобразования дробей. Выполнять действия с алгебраическими дробями. Представлять целое выражение в виде многочлена, дробное -в виде отношения многочленов; доказывать тождества. Формулировать определение степени с целым показателем. Формулировать, записывать в символической форме и иллюстрировать примерами свойства степени с целым показателем; применять свойства степени для преобразования выражений и вычислений. Доказывать свойства арифметических квадратных корней; применять их к преобразованию выражений. Вычислять значения выражений, содержащих квадратные корни; выражать переменные из геометрических и физических формул. Исследовать уравнение х2 = а; находить точные и приближенные корни при я0 |
| Уравнения (65 ч.) |
| 7 класс. Уравнения (22ч.) Выражения, тождества, уравнения (8ч.) Уравнение с одной переменной. Корень уравнения. Свойства числовых равенств. Равносильность уравнений. Линейное уравнение с одной переменной. Решение задач с помощью уравнения. Системы линейных уравнений (14ч.) Линейное уравнение с двумя переменными. График линейного уравнения с двумя переменными. Корни уравнения. Система уравнений с двумя переменными. Равносильность систем. Системы двух линейных уравнений с двумя переменными; решение подстановкой и сложением. Решение текстовых задач алгебраическим способом. 8 класс. Уравнения (22ч.) Квадратные уравнения (22ч.) Квадратное уравнение: формула корней квадратного уравнения. Неполные квадратные уравнения. Теорема Виета. Биквадратные уравнения. Решение уравнений, сводящихся к линейным и квадратным. Решение дробно-рациональных уравнений. Решение текстовых задач алгебраическим способом. 9 класс. Уравнения (21ч.) Уравнения и неравенства с одной переменной ( 8ч.) Целое уравнение и его корни. Примеры решения уравнений третьей и четвертой степени разложением на множители. Дробные рациональные уравнения. Решение текстовых задач алгебраическим способом.
|
Умение решать уравнения вида ах = b при различных значениях а и b, а также несложные уравнения, сводящиеся к ним,решать основные виды линейных уравнений с одной переменной, системы двух уравнений с двумя переменными; понимать уравнение как важнейшую математическую модель для описания и изучения разнообразных реальных ситуаций, решать текстовые задачи алгебраическим методом; применять графические представления для исследования уравнений
Определять, является ли пара чисел решением данного уравнения с двумя переменными; приводить примеры решений уравнений с двумя переменными. Решать задачи, алгебраической моделью которых является уравнение с двумя переменными, находить целые решения путем перебора. Решать системы двух уравнений с двумя переменными, указанные в содержании. Решать текстовые задачи алгебраическим способом: переходить от словесной формулировки условия задачи к алгебраической модели путем составления системы уравнений; решать составленную систему уравнений; интерпретировать результат. Строить графики уравнений с двумя переменными. Конструировать эквивалентные речевые высказывания с использованием алгебраического и геометрического языков. Использовать функционально-графические представления для решения и исследования уравнений и систем. |
| Неравенства (20ч.) |
| 8 класс. Неравенства ( 10ч.) Неравенства (10ч.) Числовые неравенства и их свойства. Числовые промежутки. Координатная прямая. Неравенство с одной переменной. Равносильность неравенств. Линейные неравенства с одной переменной. Системы неравенств с одной переменной. 9 класс. Неравенства ( 10ч.) Уравнения и неравенства с одной переменной ( 6ч.) Неравенства второй степени с одной переменной. Квадратные неравенства. Примеры решения дробно-рациональных неравенств. Метод интервалов. Уравнения и неравенства с двумя переменными(4ч.) Неравенства с двумя переменными. Системы неравенств с двумя переменными. Графическая интерпретация неравенств и систем неравенств с двумя переменными.
|
Формулировать свойства числовых неравенств, иллюстрировать их на координатной прямой, доказывать алгебраически; применять свойства неравенств в ходе решения задач. Распознавать линейные и квадратные неравенства. Решать линейные неравенства, системы линейных неравенств. Решать квадратные неравенства, используя графические представления
|
| Зависимости между величинами (13 ч.) |
| Зависимости между величинами (13 ч.) 7 класс. Зависимости между величинами (6 ч.) Функции (6ч.) 1)Зависимость между величинами. 2)Представление зависимостей между величинами в виде формул. 3)Вычисления по формулам. 4)Прямая пропорциональная зависимость: задание формулой, коэффициент пропорциональности, свойства 5) Примеры прямо пропорциональных зависимостей. Решение задач на прямую пропорциональную зависимость. 9 класс. Основные понятия функции (7 ч.) Свойства функций. Квадратичная функция(7ч.) Обратная пропорциональная зависимость: задание формулой, коэффициент обратной пропорциональности; свойства. Примеры обратных пропорциональных зависимостей. Решение задач на обратную пропорциональную зависимость. Свойства функций, их отображение на графике. Примеры графиков зависимостей, отражающих реальные процессы.
|
Составлять формулы, выражающие зависимости между величинами, вычислять по формулам. Распознавать прямую и обратную пропорциональные зависимости. Решать текстовые задачи на прямую и обратную пропорциональные зависимости (в том числе с контекстом из смежных дисциплин, из реальной жизни) |
| Числовые функции (25 ч.) |
| 7 класс. Числовые функции (8 ч.) Функции (6 ч.) 1)Понятие функции. 2)Область определения и множество значений функции 3)Функции, описывающие прямую пропорциональную зависимость. Прямая пропорциональность, ее график и свойства. Линейная функция, ее график и свойства. Построение графиков прямой пропорциональности, линейной функции. Задание функции несколькими способами. Степень с натуральным показателем (2 ч.) Функции у = х2, у=х3, их графики. 8 класс. Числовые функции (5 ч.) Рациональные дроби (3 ч.) Функция, описывающая обратную пропорциональную зависимость, ее график и свойства. Квадратные корни ( 2ч.) Функция у=√х, ее график и свойства. 9 класс. Числовые функции (12 ч.) Свойства функций. Квадратичная функция(12ч.) Способы задания функции. График функции. Свойства функции, их отображение на графике: возрастание и убывание функции, нули функции, сохранение знака. Чтение и построение графиков функций. Примеры графиков, отражающих реальные процессы. Квадратичная функция, ее график и свойства. Степенные функции с натуральными показателями 2 и 3, их графики и свойства.
|
Вычислять значения функций, заданных формулами (при необходимости использовать калькулятор); составлять таблицы значений функций. Строить по точкам графики функций. Описывать свойства функции на основе ее графического представления. Моделировать реальные зависимости с помощью формул и графиков. Интерпретировать графики реальных зависимостей. Использовать функциональную символику для записи разнообразных фактов, связанных с рассматриваемыми функциями, обогащая опыт выполнения знаково-симво-лических действий. Строить речевые конструкции с использованием функциональной терминологии. Использовать компьютерные программы для исследования положения на координатной плоскости графиков функций в зависимости от значений коэффициентов, входящих в формулу. Распознавать виды изучаемых функций. Показывать схематически положение на координатной плоскости графиков функций вида у = kx, у — kx ~ b, у = —, у = ах2, у=ах2+с, у = ах2 + Ьх+с в зависимости от значений коэффициентов,входящих в формулы. Строить графики изучаемых функций; описывать их свойства |
| Числовые последовательности. (15ч) |
| 9 класс. Числовые последовательности (15ч.) Понятие числовой последовательности. Задание последовательности рекуррентной формулой и формулой n-го члена. Арифметическая и геометрическая прогрессии. Формулы n-го члена арифметической и геометрической прогрессий, суммы первых п членов. Изображение членов арифметической и геометрической прогрессий точками координатной плоскости. Линейный и экспоненциальный рост. Сложные проценты.
| Применять индексные обозначения, строить речевые высказывания с использованием терминологии, связанной с понятием последовательности. Вычислять члены последовательностей, заданных формулой n-го члена или рекуррентной формулой. Устанавливать закономерность в построении последовательности, если выписаны первые несколько ее членов. Изображать члены последовательности точками на координатной плоскости. Распознавать арифметическую и геометрическую прогрессии при разных способах задания. Выводить на основе доказательных рассуждений формулы общего члена арифметической и геометрической прогрессий, суммы первых л членов арифметической и геометрической прогрессий; решать задачи с использованием этих формул. Рассматривать примеры из реальной жизни, иллюстрирующие изменение в арифметической прогрессии, в геометрической прогрессии; изображать соответствующие зависимости графически. Решать задачи на сложные проценты, в том числе задачи из реальной практики (с использованием калькулятора) |
| Описательная статистика (5ч.) |
| 7 класс. Описательная статистика (5 ч.) Выражения, тождества, уравнения (5ч.) Представление данных в виде таблиц, диаграмм, графиков. Случайная изменчивость. Статистические характеристики набора данных: среднее арифметическое, медиана, наибольшее и наименьшее значения, размах, дисперсия. Репрезентативные и нерепрезентативные выборки.
|
Извлекать информацию из таблиц и диаграмм, выполнять вычисления по табличным данным. Определять по диаграммам наибольшие и наименьшие данные, сравнивать величины. Организовывать информацию в виде таблиц, столбчатых и круговых диаграмм, в том числе с помощью компьютерных программ. Приводить примеры числовых данных (цена, рост, время на дорогу и т. д.), находить среднее арифметическое, размах, дисперсию числовых наборов. Приводить содержательные примеры использования средних и дисперсии для описания данных (уровень воды в водоеме, спортивные показатели, определение границ климатических зон) |
| Случайные события и вероятность. (5 ч.) |
| 8 класс. Случайные события и вероятность. (5ч.) Понятие о случайном опыте и случайном событии. Элементарные события. Частота случайного события. Статистический подход к понятию вероятности. Несовместные события. Формула сложения вероятностей. Вероятности противоположных событий. Независимые события. Умножение вероятностей. Достоверные и невозможные события. Равновозможность событий. Классическое определение вероятности
|
Проводить случайные эксперименты, в том числе с помощью компьютерного моделирования, интерпретировать их результаты. Вычислять частоту случайного события; оценивать вероятность с помощью частоты, полученной опытным путем. Приводить примеры достоверных и невозможных событий. Объяснять значимость маловероятных событий в зависимости от их последствий. Решать задачи на нахождение вероятностей событий. Приводить примеры противоположных событий. Использовать при решении задач свойство вероятностей противоположных событий |
| Элементы комбинаторики и теории вероятностей (8ч.) |
| 9 класс. Элементы комбинаторики и теории вероятностей. (8ч.) Решение комбинаторных задач перебором вариантов. Комбинаторное правило умножения. Перестановки и факториал. Относительная частота и вероятность случайного события. Сложение и умножение вероятностей.
|
Выполнять перебор всех возможных вариантов для пересчета объектов или комбинаций. Применять правило комбинаторного умножения для решения задач на нахождение числа объектов или комбинаций (диагонали многоугольника, рукопожатия, число кодов, шифров, паролей и т. п.). Распознавать задачи на определение числа перестановок и выполнять соответствующие вычисления. Решать задачи на вычисление вероятности с применением комбинаторики |
| Множества. Элементы логики (5 ч.) |
| 9 класс. Множества. Элементы логики. (5 ч.) Определение. Аксиомы и теоремы. Доказательство. Доказательство от противного. Теорема, обратная данной. Пример и контрпример. Иллюстрация отношений между множествами с помощью диаграмм Эйлера-Венна. Понятие о равносильности, следовании, употребление логических связок если ..., то ..., в том и только том случае. Логические связки и, или | Воспроизводить формулировки определений; конструировать несложные определения самостоятельно. Воспроизводить формулировки и доказательства изученных теорем, проводить несложные доказательства самостоятельно, ссылаться в ходе обоснований на определения, теоремы, аксиомы. Иллюстрировать математические понятия и утверждения примерами. Использовать примеры и контрпримеры в аргументации. Конструировать математические предложения с помощью связок если ..., то ..., в том и только том случае, логических связок и, или |
| МАТЕМАТИКА ( ГОМЕТРИЯ) 204 ч. |
| Геометрические фигуры (102 ч) |
| 7 класс. Геометрические фигуры (40 ч.) Начальные геометрические сведения (8ч.) Точка, прямая, плоскость. Отрезок, луч. Угол. Прямой угол, острый и тупой углы, развернутый угол. Вертикальные и смежные углы. Биссектриса угла и ее свойства. Свойства углов с параллельными и перпендикулярными сторонами. Перпендикулярные прямые.
Треугольники (11ч.) Треугольник. Прямоугольные, остроугольные, тупоугольные треугольники. Первый признак равенства треугольников. Решение задач на применение первого признака равенства треугольников. Высота, медиана, биссектриса. Равнобедренные и равносторонние треугольники. Свойства и признаки равнобедренного треугольника. Второй признак равенства треугольников. Решение задач на применение второго признака равенства треугольников. Третий признак равенства треугольников. Решение задач на применение третьего признака равенства треугольников.
Параллельные прямые (10ч.) Параллельные и пересекающиеся прямые. Определение параллельных прямых. Признаки параллельности прямых. Решение задач на применение признаков параллельности прямых. Об аксиомах геометрии. Аксиома параллельных прямых. Свойства параллельных прямых. Решение задач на применение свойств параллельных прямых. Теоремы об углах, образованных двумя параллельными прямыми и секущей. Решение задач на нахождение углов, образованных двумя параллельными прямыми и секущей. Соотношения между сторонами и углами треугольника (11ч.) Сумма углов треугольника. Решение задач на применение теоремы о сумме углов треугольника. Соотношения между сторонами и углами треугольника. Внешние углы треугольника. Неравенство треугольника. Прямоугольные треугольники и их свойства. Решение задач на применение свойств прямоугольного треугольника. Признаки равенства прямоугольных треугольников. Применение признаков равенства прямоугольных треугольников при решении задач. Перпендикуляр и наклонная к прямой. 8 класс. Геометрические фигуры (50 ч.) Четырехугольники (12ч.) Многоугольник. Выпуклые многоугольники. Сумма углов выпуклого многоугольника. Четырехугольник. Параллелограмм, его свойства и признаки. Теорема Фалеса. Прямоугольник, его свойства и признаки. Квадрат, его свойства и признаки. Ромб, его свойства и признаки. Трапеция, средняя линия трапеции. Площади фигур (4ч.) Теорема Пифагора. Теорема, обратная теореме Пифагора. Подобные треугольники (19ч.) Подобие треугольников. Признаки подобия треугольников. средняя линия треугольника Пропорциональные отрезки в прямоугольном треугольнике. Синус, косинус, тангенс, котангенс острого угла прямоугольного треугольника. Окружность (15ч.) Окружность и круг. Дуга, хорда. Сектор, сегмент. Центральный угол, вписанный угол; величина вписанного угла. Взаимное расположение прямой и окружности, двух окружностей. Касательная и секущая к окружности, их свойства. Серединный перпендикуляр к отрезку. Геометрическое место точек. Свойства биссектрисы угла и серединного перпендикуляра к отрезку. Решение задач на вычисление, доказательство с использованием свойств изученных фигур. 9 класс. Геометрические фигуры (12 ч.) Длина окружности и площадь круга (2ч.) Правильные многоугольники. Вписанные и описанные многоугольники. Окружность, вписанная в треугольник, и окружность, описанная около треугольника. Вписанные и описанные окружности правильного многоугольника. Начальные сведения из стереометрии (10ч.) Наглядные представления о пространственных телах. Куб, параллелепипед, призма, пирамида, шар, сфера, конус, цилиндр. Примеры сечений. Примеры разверток.
|
Устанавливать и характеризовать взаимное расположение точек, прямых, отрезков; находить длины отрезков и расстояния между двумя точками; характеризовать взаимное расположение сторон пар смежных и вертикальных углов; по данной градусной мере одного из вертикальных или смежных углов находить градусную меру другого; через данную точку проводить прямую, перпендикулярную данной прямой определять виды углов, обозначать их, развивать практические навыки работы с чертежом, воспитывать эстетическое восприятие изучаемого материала, применять знания из других областей
Находить соответственные элементы двух равных треугольников; использовать признаки равенства для доказательства равенства треугольников; изображать медианы, биссектрисы, высоты треугольника; формулировать определения и иллюстрировать понятия равных треугольников, равнобедренного, равностороннего, формулировать и доказывать теоремы о свойствах и признаках равнобедренного треугольника использовать их свойства при решении задач; использовать свойства равнобедренного и равностороннего треугольников при решении задач; изображать на рисунке треугольник, заданный своими элементами
Распознавать на чертежах, изображать параллельные прямые, формулировать определения параллельных прямых; углов, образованных при пересечении двух параллельных прямых секущей; перпендикулярных прямых; перпендикуляра и наклонной к прямой; серединного перпендикуляра к отрезку. Объяснять, что такое геометрическое место точек, приводить примеры геометрических мест точек. Формулировать аксиому параллельных прямых. Формулировать и доказывать теоремы, выражающие свойства вертикальных и смежных углов, свойства и признаки параллельных прямых, о единственности перпендикуляра к прямой, свойстве перпендикуляра и наклонной, свойствах биссектрисы угла и серединного перпендикуляра к отрезку. Решать задачи на построение, доказательство и вычисления. Выделять в условии задачи условие и заключение. Распознавать на чертежах, формулировать определения, изображать прямоугольный, остроугольный, тупоугольный, равнобедренный, равносторонний треугольники; высоту, медиану, биссектрису, среднюю линию треугольника. Формулировать определение равных треугольников. Формулировать и доказывать теоремы о признаках равенства треугольников. Объяснять и иллюстрировать неравенство треугольника. Формулировать и доказывать теоремы о свойствах и признаках равнобедренного треугольника, соотношениях между сторонами и углами треугольника, сумме углов треугольника, внешнем угле треугольника, о средней линии треугольника. Формулировать определение подобных треугольников. Формулировать и доказывать теоремы о признаках подобия треугольников, теорему Фалеса. Формулировать и доказывать теоремы о точках пересечения серединных перпендикуляров, биссектрис, медиан, высот или их продолжений. Исследовать свойства треугольника с помощью компьютерных программ. Решать задачи на построение, доказательство и вычисления. Выделять в условии задачи условие и заключение. Моделировать условие задачи с помощью чертежа или рисунка, проводить дополнительные построения в ходе решения. Опираясь на данные условия задачи, проводить необходимые рассуждения. Интерпретировать полученный результат и сопоставлять его с условием задачи. Распознавать, формулировать определение и изображать параллелограмм, прямоугольник, квадрат, ромб, трапецию, равнобедренную и прямоугольную трапеции, среднюю линию трапеции. Формулировать и доказывать теоремы о свойствах и признаках параллелограмма, прямоугольника, квадрата, ромба, трапеции. Исследовать свойства четырехугольников с помощью компьютерных программ. Решать задачи на построение, доказательство и вычисления. Моделировать условие задачи с помощью чертежа или рисунка, проводить дополнительные построения в ходе решения. Выделять на чертеже конфигурации, необходимые для проведения обоснований логических шагов решения. Формулировать определения понятий, связанных с окружностью, секущей и касательной к окружности, углов, связанных с окружностью. Формулировать и доказывать теоремы об углах, связанных с окружностью. Изображать, распознавать и описывать взаимное расположение прямой и окружности. Изображать и формулировать определения вписанных и описанных многоугольников и треугольников; окружности, вписанной в треугольник, и окружности, описанной около треугольника. Формулировать и доказывать теоремы о вписанной и описанной окружностях треугольника и многоугольника. Исследовать свойства конфигураций, связанных с окружностью, с помощью компьютерных программ. Распознавать многоугольники, формулировать определение и приводить примеры многоугольников. Формулировать и доказывать теорему о сумме углов выпуклого многоугольника. Исследовать свойства многоугольников с помощью компьютерных программ. Решать задачи на доказательство и вычисления. Моделировать условие задачи с помощью чертежа или рисунка, проводить дополнительные построения в ходе решения. Интерпретировать полученный результат и сопоставлять его с условием задачи |
| Измерение геометрических величин (35 ч.) |
| 7 класс. Измерение геометрических величин ( 5 ч.) Начальные геометрические сведения (3ч.) Измерение отрезков. Длина ломаной. Измерение углов. Соотношение между сторонами и углами треугольника (2ч.) Расстояние от точки до прямой. Расстояние между параллельными прямыми. 8 класс. Измерение геометрических величин (10ч.) Площади фигур (10ч.) Понятие площади плоских фигур. Равносоставленные и равновеликие фигуры. Площадь прямоугольника. Площади параллелограмма, треугольника и трапеции. Соотношение между площадями подобных фигур. Решение задач на вычисление и доказательство с использованием изученных формул. 9класс. Измерение геометрических величин. (20ч.) Соотношения между сторонами и углами треугольника(10ч.) Решение прямоугольных треугольников. Синус, косинус, тангенс, котангенс острого угла прямоугольного треугольника. и углов от 0 до 180°; приведение к острому углу Основное тригонометрическое тождество. Формулы, связывающие синус, косинус, тангенс, котангенс одного и того же угла. Решение треугольников: теорема косинусов и теорема синусов. Замечательные точки треугольника. Формулы, выражающие площадь треугольника: через две стороны и угол между ними. Длина окружности и площадь круга (10 ч.) Периметр многоугольника. Длина окружности, число пи; длина дуги окружности. Градусная мера угла, соответствие между величиной центрального угла и длиной дуги окружности. Площадь правильного многоугольника. Формулы, выражающие площадь треугольника: через периметр и радиус вписанной окружности, формула Герона. Площадь круга и площадь сектора.
Связь между площадями подобных фигур. Объем тела. Формулы объема прямоугольного параллелепипеда, куба, шара, цилиндра и конуса.
|
Находить длины отрезков и расстояния между двумя точками Формулировать и объяснять свойства длины, градусной меры угла. Формулировать определения расстояния между точками, от точки до прямой, между параллельными прямыми.
Формулировать и объяснять свойства длины, градусной меры угла, площади. Формулировать соответствие между величиной центрального угла и длиной дуги окружности. Объяснять и иллюстрировать понятия равновеликих и равносоставленных фигур. Выводить формулы площадей прямоугольника, параллелограмма, треугольника и трапеции, а также формулу, выражающую площадь треугольника через две стороны и угол между ними, длину окружности, площадь круга. Находить площадь многоугольника разбиением на треугольники и четырехугольники. Объяснять и иллюстрировать отношение площадей подобных фигур. Решать задачи на вычисление линейных величин, градусной меры угла и площадей треугольников, четырехугольников и многоугольников, длины окружности и площади круга. Опираясь на данные условия задачи, находить возможности применения необходимых формул, преобразовывать формулы. Использовать формулы для обоснования доказательных рассуждений в ходе решения. Интерпретировать полученный результат и сопоставлять его с условием задачи. Формулировать определения и иллюстрировать понятия синуса, косинуса, тангенса и котангенса острого угла прямоугольного треугольника. Выводить формулы, выражающие функции угла прямоугольного треугольника через его стороны. Формулировать и доказывать теорему Пифагора. Формулировать определения синуса, косинуса, тангенса, котангенса углов от 0° до 180 Выводить формулы, выражающие функции углов от 0° до 180° через функции острых углов. Формулировать и разъяснять основное тригонометрическое тождество. Вычислять значение функции угла по одной из его заданных функций. Формулировать и доказывать теоремы синусов и косинусов.
|
| Построения с помощью циркуля и линейки (17 ч.) |
| 7 класс. Построения с помощью циркуля и линейки (15ч.) Треугольники (7ч.) Деление отрезка на п равных частей. Построение угла, равного данному. Построение биссектрисы угла. Построение перпендикуляра к прямой. Деление отрезка пополам.
Параллельные прямые (3ч.) Практические способы построения параллельных прямых. Соотношения между сторонами и углами треугольника (5ч.) Основные задачи на построение треугольников. Построение треугольника по трем элементам.
8 класс. Построения с помощью циркуля и линейки (2ч.) Окружность (2ч.) Построение серединного перпендикуляра к отрезку.
|
Находить условия существования решения задачи на построение с помощью циркуля и линейки, доказывать, что построенная фигура удовлетворяет условиям задачи, проводить необходимые доказательные рассуждения. уверенно пользоваться чертежными инструментами.
Выполнять построение параллельных прямых, Находить условия существования решения, выполнять необходимых для построения искомой фигуры, доказывать, что построенная фигура удовлетворяет условиям задачи (определять число решений задачи при каждом возможном выборе данных)
Решать задачи на построение, строить треугольник по заданным элементам, доказывать, что построенная фигура удовлетворяет условиям задачи, оценивать правильность выполнения действий на уровне адекватной ретроспективной оценки, выделять в условии задачи условие и заключение, сопоставлять полученный результат с условием задачи.
|
| Геометрические преобразования (10 ч.) |
| 8 класс. Геометрические преобразования (2ч.) Четырехугольники(2ч.) Понятие о равенстве фигур. Понятие о движении: осевая и центральная симметрии. 9 класс. Геометрические преобразования (8ч.) Понятие о движении. Параллельный перенос, поворот. Понятие о подобии фигур и гомотетии.
|
Объяснять и иллюстрировать понятия равенства фигур, подобия. Строить равные и симметричные фигуры, выполнять параллельный перенос и поворот. Исследовать свойства движений с помощью компьютерных программ. Выполнять проекты по темам геометрических преобразований на плоскости. |
| Векторы(10ч). |
| Длина (модуль) вектора. Равенство векторов. Коллинеарные векторы. Координаты вектора. Умножение вектора на число, сумма векторов, разложение вектора по двум неколлинеарным векторам. Скалярное произведение векторов. Применение векторов к решению задач.
| Формулировать определения и иллюстрировать понятия вектора, длины (модуля) вектора, коллинеарных векторов, равных векторов. Вычислять длину и координаты вектора. Находить угол между векторами. Выполнять операции над векторами. Выполнять проекты по темам использования векторного метода при решении задач на вычисления и доказательства |
| Координаты. (10ч) |
| Разложение вектора по двум неколлинеарным векторам. Координаты вектора. Связь между координатами вектора и координатами его начала и конца. Координаты середины отрезка. Вычисление длины вектора. Формула расстояния между двумя точками плоскости. Уравнение линии на плоскости. Уравнение прямой. Уравнение окружности.
| Объяснять и иллюстрировать понятие декартовой системы координат. Выводить и использовать формулы координат середины отрезка, расстояния между двумя точками плоскости, уравнения прямой и окружности. Выполнять проекты по темам использования координатного метода при решении задач на вычисления и доказательства. |
VII. Описание учебно-методического и материально-технического обеспечения образовательного процесса по предмету МАТЕМАТИКА.
Оснащение процесса обучения математике обеспечивается библиотечным фондом печатными пособиями, а также информационно-коммуникативными средствами, экранно-звуковыми пособиями, техническими средствами обучения, учебно-практическим и учебно-лабораторным оборудованием.
.
1. Библиотечный фонд
1.1. Нормативные документы: Примерные программы по учебным предметам. Математика 5-9 классы. Москва «Просвещение» 2011 г.
1.2. Бунимович Е.А., Кузнецов Л.В., Минаев С.С., Рослова Л.О., Суворова С.Б. «Рабочие программы «МАТЕМАТИКА». Предметная линия учебников «СФЕРЫ»». –М.: Просвещение.2011г.
1.3. Учебники:
Бунимович Е.А. Математика. Арифметика. Геометрия. 5 класс: учебник для общеобразовательных учреждений./ Е.А.Бунимович, Г.В.Дорофеев, С.Б.Суворова и др. – М.: Просвещение,2013.
Электронное приложение к учебниу. – М.: Просвещение,2013.
Бунимович Е.А. Математика. Арифметика. Геометрия. 6 класс: учебник для общеобразовательных учреждений./ Е.А.Бунимович, Г.В.Дорофеев, С.Б.Суворова и др. – М.: Просвещение,2013.
Электронное приложение к учебниу. – М.: Просвещение,2013.
Л.С.Атанасян, В.Ф.Бутузов «Геометрия 7-9» М.Просвещение, 2015 г.
Ю.Н. Макарычев, Н.Г. Миндюк и др. «Алгебра, 7» М. Просвещение, 2015 г
Ю.Н. Макарычев, Н.Г. Миндюк и др. «Алгебра, 8» М. Просвещение, 2015 г
Ю.Н. Макарычев, Н.Г. Миндюк и др. «Алгебра, 9» М. Просвещение, 2015 г
1.4.Учебные пособия:
Бунимович Е.А. Математика. Арифметика. Геометрия. Тетрадь-тренажер. 5 класс: пособие для учащихся общеобразовательных учреждений./ Е.А.Бунимович, Л.В.Кузнецова, С.С.Минаева и др. – М. Просвещение,2013.
Бунимович Е.А. Математика. Арифметика. Геометрия. Тетрадь-тренажер. 6 класс: пособие для учащихся общеобразовательных учреждений./Е.А.Бунимович, Л.В.Кузнецова, С.С.Минаева и др. – М.: Просвещение,2013.
Бунимович Е.А. Математика. Арифметика. Геометрия. Тетрадь-экзаменатор. 5 класс: пособие для учащихся общеобразовательных учреждений./ Е.А.Бунимович, Л.В.Кузнецова, С.С.Минаева и др. – М.: Просвещение,2013.
Бунимович Е.А. Математика. Арифметика. Геометрия. Тетрадь-экзаменатор. 6 класс: пособие для учащихся общеобразовательных учреждений./ Е.А.Бунимович, Л.В.Кузнецова, С.С.Минаева и др. – М.: Просвещение,2013.
Бунимович Е.А. Математика. Арифметика. Геометрия. Задачник. 5 класс: пособие для учащихся общеобразовательных учреждений./ Е.А.Бунимович, Л.В.Кузнецова, С.С.Минаева и др. – М.: Просвещение,2013
Бунимович Е.А. Математика. Арифметика. Геометрия. Задачник. 6 класс: пособие для учащихся общеобразовательных учреждений./ Е.А.Бунимович, Л.В.Кузнецова, С.С.Минаева и др. – М.: Просвещение,2013.
1.5.Дидактический материал:
Л.И.Звавич, Л.В.Кузнецова, С.Б.Суворова «Дидактические материалы по алгебре» 7 класс. М.: «Просвещение» 2012
Л.И.Звавич, Л.В.Кузнецова, С.Б.Суворова «Дидактические материалы по алгебре» 8 класс. М.: «Просвещение» 2012
Л.И.Звавич, Л.В.Кузнецова, С.Б.Суворова «Дидактические материалы по алгебре» 9 класс. М.: «Просвещение» 2012
Ершова А.И. Ершова А.С., Голобородько В.В. «Математика 5 кл. Самостоятельные и контрольные работы». М. «Илекса», 2012г
Ершова А.И. Ершова А.С., Голобородько В.В. «Математика 6 кл. Самостоятельные и контрольные работы». М. «Илекса», 2012г
Чесноков Д.М. Дидактический материал по математике 5 кл. М.: «Просвещение» 2012 г.
Чесноков Д.М. Дидактический материал по математике 6 кл. М.: «Просвещение» 2012 г.
Ершова А.И., Ершова А.С., Голобородько В.В. «Алгебра, геометрия 7 кл. Самостоятельные и контрольные работы». М.: «Илекса», 2012г
Ершова А.И., Ершова А.С., Голобородько В.В. «Алгебра, геометрия 7 кл. Самостоятельные и контрольные работы». М.: «Илекса», 2012г
Ершова А.И., Ершова А.С., Голобородько В.В. «Алгебра, геометрия 7 кл. Самостоятельные и контрольные работы». М.: «Илекса», 2012г
2. Печатные пособия.
2.1.Таблицы по математике для 5-6 классов.
2.2.Портреты выдающихся деятелей математики.
2.3. Набор таблиц по алгебре для 7-9 классов.
2.4 Набор таблиц по геометрии для 7-9 классов.
3. Информационные средства
3.1.Мультимедийные обучающие программы и электронные издания по основным разделам курса математики.
3.2.Электронная база данных для создания тематических и итоговых разноуровневых тренировочных и проверочных материалов для организации фронтальной и индивидуальной работы.
3.3.Инструментальная среда по математике.
3.4.Сайт интернет - поддержки УМК «Сферы»: www.spheres.ru
3.5 Интерактивное учебное пособие «Наглядная математика»
4. Экранно – звуковые пособия.
4.1Видеофильмы по истории развития математики, математических идей и методов.
4.2 Презентации к урокам.
5. Технические средства обучения.
5.1.Ноутбук.
5.2.Мультимедиапроектор.
5.3.Экран (на штативе или навесной)
6. Учебно - практическое и учебно-лабораторное оборудование.
6.1.Комплект чертёжных инструментов (классных и раздаточных), линейка, транспортир, угольник (300, 600, 900), угольник (450, 90), циркуль.
6.2.Комплекты планиметрических и стереометрических тел (демонстрационных и раздаточных).
6.3.Комплект для моделирования (цветная бумага, картон, калька, клей, ножницы, пластилин).
VIII. Планируемые результаты учебного предмета МАТЕМАТИКА.
Планируемые результаты изучения курса математики в 5-6 классах
В результате изучения темы «Линии» обучающиеся
должны уметь:
Различать виды линий;
Проводить и обозначать прямую, луч, отрезок, ломаную;
Строить отрезок заданной длины и находить длину отрезка;
Распознавать окружность; проводить окружность заданного радиуса;
Переходить от одних единиц измерения длины к другим единицам, выбирать подходящие единицы измерения в зависимости от контекста задачи.
получат возможность:
В результате изучения темы «Натуральные числа» обучающиеся
должны уметь:
Понимать особенности десятичной системы счисления; знать названия разрядов и классов (в том числе «миллион»и «миллиард»);
Читать и записывать натуральные числа ,используя также и сокращённые обозначения (тыс., млн, млрд); уметь представлять натуральное число в виде суммы разрядных слагаемых;
Приобрести опыт чтения чисел, записанных римскими цифрами, используя в качестве справочного материала таблицу значений таких цифр, как L,C,D,M; читать и записывать римскими цифрами числа в простейших, наиболее употребительных случаях (например IV,XII,XIX);
Сравнивать и упорядочивать натуральные числа, используя для записи результата знаки и ; читать и записывать двойные неравенства;
Изображать натуральные числа точками на координатной прямой; понимать и уметь читать записи типа А(3);
Округлять натуральные числа до указанного разряда, поясняя при этом свои действия;
Знать термины «приближённое значение с недостатком» и «приближённое значение с избытком»;
Приобрести первоначальный опыт решения комбинаторных задач методом перебора всех возможных вариантов.
получат возможность:
познакомиться с позиционными системами счисления
углубить и развить представления о натуральных числах
приобрести привычку контролировать вычисления
В результате изучения темы «Действия с натуральными числами» обучающиеся
должны:
Выполнять арифметические действия с натуральными числами, находить значения числовых выражений, устанавливая порядок выполнения действий;
Знать, как связаны между собой действия сложения и вычитания, умножения и деления; знать термины «слагаемое», «вычитаемое», «делимое» и пр., находить неизвестное число в равенстве на основе зависимости между компонентами действий;
Представлять произведение нескольких равных множителей в виде степени с натуральным показателем; знать термины «степень числа», «основание степени», «показатель степени»; возводить натуральное число в натуральную степень;
Решать несложные текстовые задачи арифметическим методом;
Решать несложные текстовые задачи на движение двух объектов навстречу друг другу, на движение реке.
получат возможность:
углубить и развить представления о свойствах делимости натуральных чисел
научиться использовать приемы, рационализирующие вычисления, приобрести привычку контролировать вычисления, выбирая подходящий для ситуации способ;
ощутить гармонию чисел, подметить различные числовые закономерности, провести математическое исследование.
В результате изучения темы «Использование свойств действий при вычислениях» обучающиеся должны:
Знать и уметь записывать с помощью букв переместительное и сочетательное свойства сложения и умножения, распределительное свойство умножения относительно сложения;
В несложных случаях использовать рассмотренные свойства для преобразования числовых выражений: группировать слагаемые в сумме и множители в произведении; с помощью распределительного свойства раскрывать скобки в произведении и выносить в сумме общий множитель за скобки; выполняя преобразование выражения, записывать соответствующую цепочку равенств;
Решать арифметическим способом несложные задачи на части и на уравнение.
получат возможность:
В результате изучения темы «Углы и многоугольники» обучающиеся
должны уметь:
Распознавать углы; использовать терминологию, связанную с углами: вершина, сторона, биссектриса;
Распознавать острые, тупые, прямые, развёрнутые углы;
Измерять величину угла с помощью транспортира и строить угол заданной величины;
Строить биссектрису угла с помощью транспортира;
Распознавать многоугольники; использовать терминологию, связанную с многоугольниками: вершина, сторона, угол, диагональ; применять классификацию многоугольников;
Изображать многоугольники с заданными свойствами; разбивать многоугольник на заданные многоугольники;
Вычислять периметр многоугольника.
получат возможность:
В результате изучения темы «Делимость чисел» обучающиеся
должны уметь:
Владеть понятиями «делитель» и «кратное», понимать взаимосвязь между ними, уметь употреблять их в речи;
Понимать обозначения НОД (a;b) и НОК(a;b), уметь находить НОД и НОК в не сложных случаях;
Знать определение простого числа, уметь приводить примеры простых и составных чисел, знать некоторые элементарные сведения о простых числах .
получат возможность:
В результате изучения темы «Треугольники и четырехугольники» обучающиеся
должны:
Распознавать и изображать остроугольные, тупоугольные, прямоугольные треугольники;
Распознавать равнобедренный треугольник и использовать связанную с ним терминологию: боковые стороны, основание; распознавать равносторонний треугольник;
Строить равнобедренный треугольник по боковым сторонам и углу между ними; понимать свойство равенства углов при основании равнобедренного треугольника;
Строить прямоугольник на нелинованной бумаге с помощью чертежных инструментов;
Понимать свойства диагоналей прямоугольника; распознавать треугольники, получаемые при разбиением прямоугольника его диагоналями;
Распознавать, моделировать и изображать равные фигуры;
Изображать многоугольники с заданными свойствами; разбивать многоугольник на заданные многоугольники;
Вычислять периметр треугольника, прямоугольника, площадь прямоугольника; применять единицы измерения площади.
получат возможность:
Научиться вычислять площади фигур, составленных из двух и более прямоугольников;
Приобрести навыки исследовательской работы.
Приобрести опыт выполнения проектных работ по темам: «Периметр и площадь школьного участка», « План школьной территории».
В результате изучения темы «Дроби» обучающиеся
должны уметь:
Знать, что означают знаменатель и числитель дроби, уметь читать и записывать дроби, иллюстрировать дробь как долю целого на рисунках и чертежах;
Находить дробь от величины, опираясь на содержательный смысл понятия дроби;
Соотносить дроби и точки координатной прямой;
Понимать, в чём заключается основное свойство дроби, иллюстрировать равенство дробей с помощью рисунков и чертежей, с помощью координатной прямой;
Сокращать дроби, приводить дроби к новому знаменателю, к общему знаменателю, сравнивать и упорядочивать дроби;
Записывать в виде дроби частное двух натуральных чисел, представлять натуральное число в виде дроби.
получат возможность:
В результате изучения темы «Действия с дробями» обучающиеся
должны уметь:
Знать и записывать с помощью букв правила сложения и вычитания дробей с одинаковыми знаменателями; выполнять сложение и вычитание дробей с одинаковыми и с разными знаменателями;
Владеть приёмами выделения целой части из неправильной дроби и представления смешанной дроби в виде неправильной;
Знать и записывать с помощью букв правила умножения и деления дробей; применять правила на практике, включая случаи действий с натуральными числами и смешанными дробями;
Владеть приёмами решения задач на нахождение части целого и целого по его части;
Решать знакомые текстовые задачи, содержащие дробные данные.
получат возможность:
В результате изучения темы «Многогранники» обучающиеся
должны:
Распознавать цилиндр, конус , шар;
Распознавать многогранники; использовать терминологию, связанную с многогранниками: вершина, ребро, грань; читать проекционное изображение многогранника;
Распознавать параллелепипед, изображать его на бумаге в клетку, определять измерения; распознавать и называть пирамиду;
Распознавать развертку куба; моделировать куб из его развертки.
получат возможность:
Приобрести опыт выполнения проектных работ по темам: «Модели многогранников», «Объем классной комнаты», «Макет домика для щенка», «Многогранники в архитектуре».
Развития пространственного воображения
Углубить и развить представления о пространственных геометрических фигурах.
В результате изучения темы «Таблицы и диаграммы» обучающиеся
должны уметь:
Анализировать готовые таблицы и диаграммы, отвечать на поставленные вопросы, делать простейшие выводы из представленных данных;
Заполнять несложные таблицы, следуя инструкции.
получат возможность:
Рациональные числа
Ученик научится:
понимать особенности десятичной системы счисления;
владеть понятиями, связанными с делимостью натуральных чисел;
выражать числа в эквивалентных формах, выбирая наиболее подходящую в зависимости от конкретной ситуации;
сравнивать и упорядочивать рациональные числа;
выполнять вычисления с рациональными числами, сочетая устные и письменные приёмы вычислений, применение калькулятора;
использовать понятия и умения, связанные с пропорциональностью величин, процентами в ходе решения математических задач и задач из смежных предметов, выполнять несложные практические расчеты.
Ученик получит возможность:
познакомиться с позиционными системами счисления с основаниями, отличными от 10;
углубить и развить представления о натуральных числах и свойствах делимости;
научиться использовать приёмы, рационализирующие вычисления, приобрести привычку контролировать вычисления, выбирая подходящий для ситуации способ.
Описательная статистика
Ученик научится использовать простейшие способы представления и анализа статистических данных.
Ученик получит возможность приобрести первоначальный опыт организации сбора данных при проведении опроса общественного мнения, осуществлять их анализ, представлять результаты опроса в виде таблицы, диаграммы.
Планируемые результаты изучения курса алгебры в 7-9 классах
Действительные числа
Выпускник научится:
• использовать начальные представления о множестве действительных чисел;
• оперировать понятием квадратного корня, применять его в вычислениях.
Выпускник получит возможность:
• развить представление о числе и числовых системах от натуральных до действительных чисел; о роли вычислений в практике;
• развить и углубить знания о десятичной записи действительных чисел (периодические и непериодические дроби).
Измерения, приближения, оценки
Выпускник научится:
• использовать в ходе решения задач элементарные представления, связанные с приближёнными значениями величин.
Выпускник получит возможность:
• понять, что числовые данные, которые используются для характеристики объектов окружающего мира, являются преимущественно приближёнными, что по записи приближённых значений, содержащихся в информационных источниках, можно судить о погрешности приближения;
• понять, что погрешность результата вычислений должна быть соизмерима с погрешностью исходных данных.
Алгебраические выражения
Выпускник научится:
• оперировать понятиями «тождество», «тождественное преобразование», решать задачи, содержащие буквенные данные; работать с формулами;
• выполнять преобразования выражений, содержащих степени с целыми показателями и квадратные корни;
• выполнять тождественные преобразования рациональных выражений на основе правил действий над многочленами и алгебраическими дробями;
• выполнять разложение многочленов на множители.
Выпускник получит возможность научиться:
• выполнять многошаговые преобразования рациональных выражений, применяя широкий набор способов и приёмов;
• применять тождественные преобразования для решения задач из различных разделов курса (например, для нахождения наибольшего/наименьшего значения выражения).
Уравнения
Выпускник научится:
• решать основные виды рациональных уравнений с одной переменной, системы двух уравнений с двумя переменными;
• понимать уравнение как важнейшую математическую модель для описания и изучения разнообразных реальных ситуаций, решать текстовые задачи алгебраическим методом;
• применять графические представления для исследования уравнений, исследования и решения систем уравнений с двумя переменными.
Выпускник получит возможность:
• овладеть специальными приёмами решения уравнений и систем уравнений; уверенно применять аппарат уравнений для решения разнообразных задач из математики, смежных предметов, практики;
• применять графические представления для исследования уравнений, систем уравнений, содержащих буквенные коэффициенты.
Неравенства
Выпускник научится:
• понимать и применять терминологию и символику, связанные с отношением неравенства, свойства числовых неравенств;
• решать линейные неравенства с одной переменной и их системы; решать квадратные неравенства с опорой на графические представления;
• применять аппарат неравенств для решения задач из различных разделов курса.
Выпускник получит возможность научиться:
• разнообразным приёмам доказательства неравенств; уверенно применять аппарат неравенств для решения разнообразных математических задач и задач из смежных предметов, практики;
• применять графические представления для исследования неравенств, систем неравенств, содержащих буквенные коэффициенты.
Основные понятия. Числовые функции
Выпускник научится:
• понимать и использовать функциональные понятия и язык (термины, символические обозначения);
• строить графики элементарных функций; исследовать свойства числовых функций на основе изучения поведения их графиков;
• понимать функцию как важнейшую математическую модель для описания процессов и явлений окружающего мира, применять функциональный язык для описания и исследования зависимостей между физическими величинами.
Выпускник получит возможность научиться:
• проводить исследования, связанные с изучением свойств функций, в том числе с использованием компьютера; на основе графиков изученных функций строить более сложные графики (кусочно-заданные, с «выколотыми» точками и т. п.);
• использовать функциональные представления и свойства функций для решения математических задач из различных разделов курса.
Числовые последовательности
Выпускник научится:
• понимать и использовать язык последовательностей (термины, символические обозначения);
• применять формулы, связанные с арифметической и геометрической прогрессией, и аппарат, сформированный при изучении других разделов курса, к решению задач, в том числе с контекстом из реальной жизни.
Выпускник получит возможность научиться:
• решать комбинированные задачи с применением формул n-го члена и суммы первых n членов арифметической и геометрической прогрессии, применяя при этом аппарат уравнений и неравенств;
• понимать арифметическую и геометрическую прогрессию как функции натурального аргумента; связывать арифметическую прогрессию с линейным ростом, геометрическую — с экспоненциальным ростом.
Описательная статистика
Выпускник научится использовать простейшие способы представления и анализа статистических данных.
Выпускник получит возможность приобрести первоначальный опыт организации сбора данных при проведении опроса общественного мнения, осуществлять их анализ, представлять результаты опроса в виде таблицы, диаграммы.
Случайные события и вероятность
Выпускник научится находить относительную частоту и вероятность случайного события.
Выпускник получит возможность приобрести опыт проведения случайных экспериментов, в том числе с помощью компьютерного моделирования, интерпретации их результатов.
Комбинаторика
Выпускник научится решать комбинаторные задачи на нахождение числа объектов или комбинаций.
Выпускник получит возможность научиться некоторым специальным приёмам решения комбинаторных задач.
Планируемые результаты изучения курса геометрии в 7-9 классах
Наглядная геометрия
Выпускник научится:
• распознавать на чертежах, рисунках, моделях и в окружающем мире плоские и пространственные геометрические фигуры;
• вычислять объём прямоугольного параллелепипеда.
Выпускник получит возможность:
• научиться вычислять объёмы пространственных геометрических фигур, составленных из прямоугольных параллелепипедов;
• распознавать развёртки куба, прямоугольного параллелепипеда, правильной пирамиды, цилиндра и конуса;
• строить развёртки куба и прямоугольного параллелепипеда;
• определять по линейным размерам развёртки фигуры линейные размеры самой фигуры и наоборот;
• углубить и развить представления о пространственных геометрических фигурах;
• научиться применять понятие развёртки для выполнения практических расчётов.
Геометрические фигуры
Выпускник научится:
• пользоваться языком геометрии для описания предметов окружающего мира и их взаимного расположения;
• распознавать и изображать на чертежах и рисунках геометрические фигуры и их конфигурации;
• находить значения длин линейных элементов фигур и их отношения, градусную меру углов от 0 до 180, применяя определения, свойства и признаки фигур и их элементов, отношения фигур (равенство, подобие, симметрии, поворот, параллельный перенос);
• оперировать с начальными понятиями тригонометрии и выполнять элементарные операции над функциями углов;
• решать задачи на доказательство, опираясь на изученные свойства фигур и отношений между ними и применяя изученные методы доказательств;
• решать несложные задачи на построение, применяя основные алгоритмы построения с помощью циркуля и линейки;
• решать простейшие планиметрические задачи в пространстве.
Выпускник получит возможность:
• овладеть методами решения задач на вычисления и доказательства: методом от противного, методом подобия, методом перебора вариантов и методом геометрических мест точек;
• приобрести опыт применения алгебраического и тригонометрического аппарата и идей движения при решении геометрических задач;
• овладеть традиционной схемой решения задач на построение с помощью циркуля и линейки: анализ, построение, доказательство и исследование;
• научиться решать задачи на построение методом геометрического места точек и методом подобия;
• приобрести опыт исследования свойств планиметрических фигур с помощью компьютерных программ;
• приобрести опыт выполнения проектов по темам «Геометрические преобразования на плоскости», «Построение отрезков по формуле».
Измерение геометрических величин
Выпускник научится:
• использовать свойства измерения длин, площадей и углов при решении задач на нахождение длины отрезка, длины окружности, длины дуги окружности, градусной меры угла;
• вычислять площади треугольников, прямоугольников, параллелограммов, трапеций, кругов и секторов;
• вычислять длину окружности, длину дуги окружности;
• вычислять длины линейных элементов фигур и их углы, используя формулы длины окружности и длины дуги окружности, формулы площадей фигур;
• решать задачи на доказательство с использованием формул длины окружности и длины дуги окружности, формул площадей фигур;
• решать практические задачи, связанные с нахождением геометрических величин (используя при необходимости справочники и технические средства).
Выпускник получит возможность научиться:
• вычислять площади фигур, составленных из двух или более прямоугольников, параллелограммов, треугольников, круга и сектора;
• вычислять площади многоугольников, используя отношения равновеликости и равносоставленности;
• применять алгебраический и тригонометрический аппарат и идеи движения при решении задач на вычисление площадей многоугольников.
Координаты
Выпускник научится:
• вычислять длину отрезка по координатам его концов; вычислять координаты середины отрезка;
• использовать координатный метод для изучения свойств прямых и окружностей.
Выпускник получит возможность:
• овладеть координатным методом решения задач на вычисления и доказательства;
• приобрести опыт использования компьютерных программ для анализа частных случаев взаимного расположения окружностей и прямых;
• приобрести опыт выполнения проектов на тему «Применение координатного метода при решении задач на вычисления и доказательства».
Векторы
Выпускник научится:
• оперировать с векторами: находить сумму и разность двух векторов, заданных геометрически, находить вектор, равный произведению заданного вектора на число;
• находить для векторов, заданных координатами: длину вектора, координаты суммы и разности двух и более векторов, координаты произведения вектора на число, применяя при необходимости сочетательный, переместительный и распределительный законы;
• вычислять скалярное произведение векторов, находить угол между векторами, устанавливать перпендикулярность прямых.
Выпускник получит возможность:
• овладеть векторным методом для решения задач на вычисления и доказательства;
• приобрести опыт выполнения проектов на тему «применение векторного метода при решении задач на вычисления и доказательства».
|
СОГЛАСОВАНО
Протокол заседания методического объединения учителей математики МБОУ СОШ № 17 ст.Выселки от 27 августа 2015 года № 1 ___________ Борисова М.М. подпись руководителя МО Ф.И.О.
|
|
СОГЛАСОВАНО
Заместитель директора по УР _______________ Н.А.Панченко . 28 августа 2015 года |
82
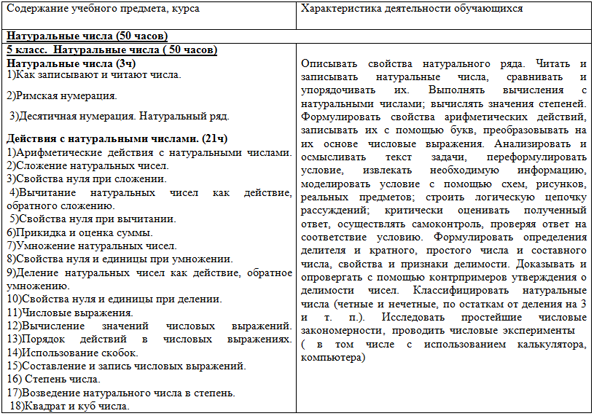

 Получите свидетельство
Получите свидетельство Вход
Вход











 Рабочая программа по математике (5-9-е классы) (0.6 MB)
Рабочая программа по математике (5-9-е классы) (0.6 MB)
 0
0 711
711 79
79 Нравится
0
Нравится
0







