Муниципальное бюджетное образовательное учреждение
средняя общеобразовательная школа № 33 имени
Героя Советского Союза Л.П. Тихмянова
УТВЕРЖДАЮ
Директор МБОУ - СОШ № 33
_____________ Н.Н. Акулова
приказ _______от ______2013 года
РАБОЧАЯ ПРОГРАММА
по геометрии
в 9 « Б » классе
2013 – 2014 учебный год
Составитель программы:
учитель математики
Панина Елена Юрьевна
Программа рассмотрена на заседании школьного методического объединения
Протокол № __ от «__»_________2013г.
Руководитель__________________________( _______ __________)
1.ПОЯСНИТЕЛЬНАЯ ЗАПИСКА.
Нормативно-правовая база.
Данная рабочая программа ориентирована на учащихся 9 классов и реализуется на основе следующих документов:
1.Закон РФ «Об образовании», п.7,ст.32;
2. Письмо Департамента образования от 13.11.2002 г. «»О развитии содержания
общего образования.
3.Программа для общеобразовательных школ, гимназий, лицеев:
Сборник “Программы для общеобразовательных школ, гимназий, лицеев:
Математика. 5-11 кл.”/ Сост. Г.М.Кузнецова, Н.Г. Миндюк. – 3-е изд., стереотип.-
М. Дрофа, 2002; 4-е изд. – 2004г.
4.Стандарт основного общего образования по математике.
Стандарт основного общего образования по математике //Математика в школе. –
2004г,-№4, -с.4
5.Федерального перечня учебников, рекомендованных Министерством образования
Российской Федерации к использованию в образовательном процессе в
общеобразовательных учреждениях на 2012-2013 учебный год,
Программы по геометрии к учебнику 7-9. Автор Атанасян Л.С., В. Ф. Бутузов, С. Б. Кадомцев и др.(Составитель программ: Т. А .Бурмистрова. «Просвещение», 2008 г. )
Учебно-методического комплекта «Геометрия, 7–9», авторы Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др.
Данная рабочая программа \ соответствует учебнику «геометрия 7-9». Автор Атанасян Л.С., В. Ф. Бутузов, С. Б. Кадомцев и др.8 г.
1.2 Место предмета в федеральном базисном учебном плане.
В соответствии с базисным учебным планом и учебным планом МБОУ –СОШ №33 г. Тулы в 9 классе на изучение курса «Геометрия» отводится 2 часа в неделю, 34 учебных недель т.е. 68 часов в год.
Причины создания рабочей программы.
Внесение данных изменений позволит охватить весь изучаемый материал по программе, повысить уровень обученности учащихся по предмету, а также более эффективно осуществить индивидуальный подход к обучающимся.
Общая характеристика учебного предмета.
Геометрия – один из важнейших компонентов математического образования. Она необходима для приобретения конкретных знаний о пространстве и практически значимых умений, формирования языка описания объектов окружающего мира, развития пространственного воображения и интуиции, математической культуры, эстетического воспитания учащихся. Изучение геометрии вносит вклад в развитие логического мышления, в формирование понятия доказательства.
В курсе геометрии 9-го класса формируется понятие вектора. Особое внимание уделяется выполнению операций над векторами в геометрической форме. Учащиеся дополняют знания о треугольниках сведениями, о методах вычисления элементов произвольных треугольниках, основанных на теоремах синусов и косинусов. Даются систематизированные сведения о правильных многоугольниках, об окружности, вписанной в правильный многоугольник и описанной. Особое место занимает решение задач на применение формул. Даются первые знания о движении, повороте и параллельном переносе. Серьезное внимание уделяется формированию умений рассуждать, делать простые доказательства, давать обоснования выполняемых действий. Параллельно закладываются основы для изучения систематических курсов стереометрии, физики, химии и других смежных предметов.
Курс характеризуется рациональным сочетанием логической строгости и геометрической наглядности. Увеличивается теоретическая значимость изучаемого материала, расширяются внутренние логические связи курса, повышается роль дедукции, степень абстрактности изучаемого материала. Учащиеся овладевают приемами аналитико-синтетической деятельности при доказательстве теорем и решении задач. Систематическое изложение курса позволяет продолжить работу по формированию представлений учащихся о строении математической теории, обеспечивает развитие логического мышления школьников. Изложение материала характеризуется постоянным обращением к наглядности, использованием рисунков и чертежей на всех этапах обучения и развитием геометрической интуиции на этой основе. Целенаправленное обращение к примерам из практики развивает умения учащихся вычленять геометрические факты, формы, и отношения.
1.5 Цели обучения.
Образовательные и воспитательные задачи обучения геометрии должны решаться комплексно с учетом возрастных особенностей обучающихся, специфики геометрии как учебного предмета, определяющего её роль и место в общей системе школьного обучения и воспитания. При планировании уроков следует иметь в виду, что теоретический материал осознается и усваивается преимущественно в процессе решения задач. Организуя решение задач, целесообразно шире использовать дифференцированный подход к учащимся. Важным условием правильной организации учебно-воспитательного процесса является выбор учителем рациональной системы методов и приемов обучения, сбалансированное сочетание традиционных и новых методов обучения, оптимизированное применение объяснительно-иллюстрированных и эвристических методов, использование технических средств, ИКТ -компонента. Учебный процесс необходимо ориентировать на рациональное сочетание устных и письменных видов работы, как при изучении теории, так и при решении задач. Внимание учителя должно быть направлено на развитие речи учащихся, формирование у них навыков умственного труда – планирование своей работы, поиск рациональных путей её выполнения, критическую оценку результатов.
Основные цели курса:
-овладение системой математических знаний и умений, необходимых в практической деятельности, продолжения образования;
-приобретение опыта планирования и осуществления алгоритмической деятельности;
-освоение навыков и умений проведения доказательств, обоснования выбора решений;
-приобретение умений ясного и точного изложения мыслей;
-развить пространственные представления и умения, помочь освоить основные факты и методы планиметрии;
-научить пользоваться геометрическим языком для описания предметов.
Задачи обучения:
- научить учащихся выполнять действия над векторами как направленными отрезками;
-познакомить с использованием векторов и метода координат при решении геометрических задач;
- развить умение учащихся применять тригонометрический аппарат при решении геометрических задач;
- расширить знания учащихся о многоугольниках;
- рассмотреть понятия длины окружности и площади круга для их вычисления;
- познакомить учащихся с понятием движения и его свойствами;
- дать начальное представление о телах и поверхностях в пространстве..
1.6 Структура рабочей программы.
Рабочая программа включает следующие разделы:
пояснительную записку;
основное содержание;
примерное распределение учебных часов по разделам программы;
требования к уровню подготовки учащихся данного класса;
тематическое планирование учебного материала;
поурочное планирование;
примерные контрольные работы;
учебное и учебно-методическое обеспечение обучения.
1.7 Обоснование увеличения/ уменьшения часов.
Данное планирование определяет достаточный объем учебного времени для повышения математических знаний учащихся в среднем звене школы, улучшения усвоения других учебных предметов.
Количество часов по темам изменено в связи со сложностью тем.
.
1.8 Формы и методы обучения.
Основной формой организации учебного процесса является классно-урочная система. В качестве дополнительных форм организации образовательного процесса по данной программе используется система консультационной поддержки, индивидуальных занятий, работа учащихся с использованием современных информационных технологий: игровое моделирование (дидактические игры, работа в малых группах, работа в парах сменного состава); проблемное обучение; личностно ориентированное обучение.
Теоретический материал курса излагается на наглядно-интуитивном уровне, математические методы и законы формулируются в виде правил. Курс строится на индуктивной основе с привлечением дедуктивных рассуждений.
Учебный процесс ориентирован на:
создание оптимальных условий обучения;
исключение психотравмирующих факторов;
сохранение психосоматического состояния здоровья учащихся;
развитие положительной мотивации к освоению программы;
развитие индивидуальности и одаренности каждого ребенка.
рациональное сочетание устных и письменных видов работы как при изучении теории, так и при решении задач;
сбалансированное сочетание традиционных и новых методов обучения;
оптимизированное применение объяснительно-иллюстративных и эвристических методов;
использование современных технических средств обучения.
2.ТРЕБОВАНИЯ К УРОВНЮ ПОДГОТОВКИ УЧАЩИХСЯ.
должны знать:
Понятие вектора. Правило сложение векторов. Определение синуса косинуса, тангенса, котангенса. Теорему синусов и косинусов. Решение треугольников. Соотношение между сторонами и углами треугольника. Определение многоугольника. Формулы длины окружности и площади круга. Свойства вписанной и описанной окружности около правильного многоугольника. Понятие движения на плоскости: симметрия, параллельный перенос, поворот.
должны уметь:
Применять вектора к решению простейших задач. Складывать, вычитать вектора, умножать вектор на число. Решать задачи, применяя теорему синуса и косинуса. Применять алгоритм решения произвольных треугольников при решении задач. Решать задачи на применение формул - вычисление площадей и сторон правильных многоугольников. Применять свойства окружностей при решении задач. Строить правильные многоугольники с помощью циркуля и линейки.
владеть компетенциями: познавательной, коммуникативной, информационной и рефлексивной.
способны решать следующие жизненно-практические задачи:
Самостоятельно приобретать и применять знания в различных ситуациях, работать в группах, аргументировать и отстаивать свою точку зрения, уметь слушать других, извлекать учебную информацию на основе сопоставительного анализа объектов, пользоваться предметным указателем энциклопедий и справочником для нахождения информации, самостоятельно действовать в ситуации неопределённости при решении актуальных для них проблем.
3.УЧЕБНО - ТЕМАТИЧЕСКИЙ ПЛАН.
|
№ |
Темы (разделы) | Ко-во часов в примерной программе | Количество часов в рабочей программе | Кол-во контрольных работ |
| 1. | Вводное повторение | - | 2 |
|
| 2. | Векторы | 18
| 8 |
|
| 3. | Метод координат | 10 | 1
|
| 4. | Соотношение между сторонами и углами треугольника | 10
| 11 | 1 |
| 5. | Длина окружности и площадь круга | 16
| 12 | 1 |
| 6. | Движение | 12
| 8 | 1 |
| 7. | Начальные сведения из стереометрии | -
| 8 |
|
| 8. | Аксиомы планиметрии | 2 | 2 |
|
| 9. | Итоговое повторение | 10 | 7 | 1 |
| Итого. |
| 68 | 68 | к.р. |
4. СОДЕРЖАНИЕ ПРОГРАММЫ УЧЕБНОГО КУРСА.
1. Векторы. Метод координат
Понятие вектора. Равенство векторов. Сложение и вычитание векторов. Умножение вектора на число. Разложение вектора по двум неколлинеарным векторам. Координаты вектора. Простейшие задачи в координатах. Уравнения окружности и прямой. Применение векторов и координат при решении задач.
О с н о в н а я ц е л ь - научить учащихся выполнять действия над векторами как направленными отрезками, что важно для применения векторов в физике; познакомить с использованием векторов и метода координат при решении геометрических задач.
Вектор определяется как направленный отрезок и действия над векторами вводятся так, как это принято в физике, т. е. как действия с направленными отрезками. Основное внимание должно быть уделено выработке умений выполнять операции над векторами (складывать векторы по правилам треугольника и параллелограмма, строить вектор, равный разности двух данных векторов, а также вектор, равный произведению данного вектора на данное число).
На примерах показывается, как векторы могут применяться к решению геометрических задач. Демонстрируется эффективность применения формул для координат середины отрезка, расстояния между двумя 'точками, уравнений окружности и прямой в конкретных геометрических задачах, тем самым дается представление об изучении геометрических фигур с помощью методов алгебры.
2. Соотношения между сторонами и углами треугольника.
Скалярное произведение векторов
Синус, косинус и тангенс угла. Теоремы синусов и косинусов. Решение треугольников. Скалярное произведение векторов и его применение в геометрических задачах.
О с н о в н а я ц е л ь - развить умение учащихся применять тригонометрический аппарат при решении геометрических задач.
Синус и косинус любого угла от 0 до 180 вводятся с помощью единичной полуокружности, доказываются теоремы синусов и косинусов и выводится еще одна формула площади треугольника (половина произведения двух сторон на синус угла между ними). Этот аппарат применяется к решению треугольников.
Скалярное произведение векторов вводится как в физике (произведение длин векторов на косинус угла между ними). Рассматриваются свойства скалярного произведения и его применение при решении геометрических задач.
Основное внимание следует уделить выработке прочных навыков в применении тригонометрического аппарата при решении геометрических задач.
3. Длина окружности и площадь круга
Правильные многоугольники. Окружности, описанная около правильного многоугольника и вписанная в него. Построение правильных многоугольников. Длина окружности. Площадь круга.
О с н о в н а я ц е л ь - расширить знание учащихся о многоугольниках; рассмотреть понятия длины окружности и площади круга и формулы для их вычисления.
В начале темы дается определение правильного многоугольника и рассматриваются теоремы об окружностях, описанной около правильного многоугольника и вписанной в него. С помощью описанной окружности решаются задачи о построении правильного шестиугольника и правильного 2п-угольника, если дан правильный п-угольник.
Формулы, выражающие сторону правильного многоугольника и радиус вписанной в него окружности через радиус описанной окружности, используются при выводе формул длины окружности и площади круга. Вывод опирается на интуитивное представление о пределе: при неограниченном увеличении числа сторон правильного многоугольника, вписанного в окружность, его периметр стремится к длине этой окружности, а площадь - к площади круга, ограниченного окружностью.
4. Движения
Отображение плоскости на себя. Понятие движения. Осевая и центральная симметрии. Параллельный перенос. Поворот. Наложения и движения.
О с н о в н а я ц е л ь - познакомить учащихся с понятием движения и его свойствами, с основными видами движений, со взаимоотношениями наложений и движений.
Движение плоскости вводится как отображение плоскости на себя, сохраняющее расстояние между точками. При рассмотрении видов движений основное внимание уделяется построению образов точек, прямых, отрезков, треугольников при осевой и центральной симметриях, параллельном переносе, повороте. На эффектных примерах показывается применение движений при решении геометрических задач.
Понятие наложения относится в данном курсе к числу основных понятий. Доказывается, что понятия наложения и движения являются эквивалентными: любое наложение является движением плоскости и обратно. Изучение доказательства не является обязательным, однако следует рассмотреть связь понятий наложения и движения.
5. Об аксиомах геометрии. Беседа об аксиомах геометрии.
О с н о в н а я ц е л ь - дать более глубокое представление о системе аксиом планиметрии и аксиоматическом методе.
В данной теме рассказывается о различных системах аксиом геометрии, в частности о различных способах введения понятия равенства фигур.
6. Начальные сведения из стереометрии
Предмет стереометрии. Геометрические тела и поверхности.
Многогранники: призма, параллелепипед, пирамида, формулы для вычисления их объемов. Тела и поверхности вращения: цилиндр, конус, сфера, шар, формулы для вычисления их площадей поверхностей и объемов.
О с н о в н а я ц е л ь - дать начальное представление о телах и поверхностях в пространстве; познакомить учащихся с основными формулами для вычисления площадей поверхностей и объемов тел.
Рассмотрение простейших многогранников (призмы, параллелепипеда, пирамиды), а также тел и поверхностей вращения (цилиндра, конyca, сферы, шара) проводится на основе наглядных представлений, без привлечения аксиом стереометрии.
7. Повторение.
КАЛЕНДАРНО ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ
ПО ГЕОМЕТРИИ В 9 КЛАССЕ
Класс: 9 « Б »
Годовое количество часов: 68
Количество часов в неделю: 2
Плановое количество контрольных работ: 5
I ч -
II ч -
III ч -
IV ч –
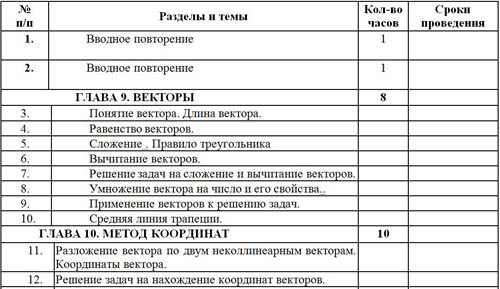
| № п/п | Разделы и темы | Кол-во часов | Сроки проведения |
-
| Вводное повторение | 1 |
|
-
| Вводное повторение | 1 |
|
| ГЛАВА 9. ВЕКТОРЫ | 8 |
|
-
| Понятие вектора. Длина вектора. |
|
|
-
| Равенство векторов. |
|
|
-
| Сложение . Правило треугольника |
|
|
-
| Вычитание векторов. |
|
|
-
| Решение задач на сложение и вычитание векторов. |
|
|
-
| Умножение вектора на число и его свойства.. |
|
|
-
| Применение векторов к решению задач. |
|
|
-
| Средняя линия трапеции. |
|
|
| ГЛАВА 10. МЕТОД КООРДИНАТ | 10 |
|
-
| Разложение вектора по двум неколлинеарным векторам. Координаты вектора. |
|
|
-
| Решение задач на нахождение координат векторов. |
|
|
-
| Связь между координатами вектора и координатами его начала и конца. |
|
|
-
| Простейшие задачи в координатах. |
|
|
-
| Решение простейших задачи в координатах. |
|
|
-
| Уравнение окружности. |
|
|
-
| Уравнение прямой. Использование уравнения прямой и окружности при решении задач. |
|
|
-
| Зачет № 1. по теме «Векторы. Метод координат» |
|
|
-
| Обобщающий урок по теме «Векторы. Метод координат» |
|
|
-
| Контрольная работа № 1. по теме «Векторы. Метод координат» |
|
|
| ГЛАВА 11. СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА | 11 |
|
-
| Анализ контрольной работы. Синус, косинус, тангенс угла. |
|
|
-
| Основное тригонометрическое тождество и формулы приведения. |
|
|
-
| Формулы для вычисления координат точки. |
|
|
-
| Теорема о площади треугольника. |
|
|
-
| Теорема синусов. Решение задач. |
|
|
-
| Теорема косинусов. Решение задач. |
|
|
-
| Решение треугольников. Измерительные работы. |
|
|
-
| Угол между векторами. Скалярное произведение векторов. Решение задая |
|
|
-
| Скалярное произведение в координатах и его свойства. Решение задач. |
|
|
-
| Зачет № 2 по теме « Соотношения между сторонами и углами треугольника. Скалярное произведение векторов.». |
|
|
-
| Контрольная работа № 2 по теме « Соотношения между сторонами и углами треугольника. Скалярное произведение векторов.». |
|
|
| ГЛАВА 12. ДЛИНА ОКРУЖНОСТИ И ПЛОЩАДЬ КРУГА. | 12 |
|
-
| Анализ контрольной работы. Правильные многоугольники и окружность, описанная около правильного многоугольника. |
|
|
-
| Окружность, вписанная в правильный многоугольник. |
|
|
-
| Формулы для вычислений площади правильного многоугольника, его стороны и радиуса вписанной окружности. |
|
|
-
| Построение правильных многоугольников. |
|
|
-
| Длина окружности. |
|
|
-
| Площадь круга. |
|
|
-
| Площадь кругового сектора. |
|
|
-
| Решение задач на нахождение длины окружности и площади круга. |
|
|
-
| Решение задач по теме «Правильные многоугольники. Вписанная, описанная окружность» |
|
|
-
| Зачет № 3 по теме «Длина окружности. Площадь круга» |
|
|
-
| Урок обобщения по теме «Длина окружности. Площадь круга» |
|
|
-
| Контрольная работа № 3 по теме «Длина окружности. Площадь круга» |
|
|
| ГЛАВА 13. ДВИЖЕНИЯ | 8 |
|
-
| Анализ контрольной работы .Понятие движения. |
|
|
-
| Осевая и центральная симметрия. |
|
|
-
| Решение задач на свойства осевой и центральной симметрии. |
|
|
-
| Параллельный перенос. |
|
|
-
| Поворот. |
|
|
-
| Решение задач на свойства параллельного переноса и поворот.. |
|
|
-
| Зачет № 4 по теме «Движения». |
|
|
-
| Контрольная работа № 4 по теме «Движения». |
|
|
| ГЛАВА 14. НАЧАЛЬНЫЕ СВЕДЕНИЯ ИЗ СТЕРЕОМЕТРИИ | 8 |
|
-
| Анализ контрольной работы .Предмет стереометрии. Многогранник. |
|
|
-
| Призма . Параллелепипед. |
|
|
-
| Объем тела. |
|
|
-
| Свойства прямоугольного параллелепипеда. Пирамида. |
|
|
-
| Цилиндр. Решение задач. |
|
|
-
| Конус. Решение задач. |
|
|
-
| Сфера . Шар. |
|
|
-
| Решение задач по теме «Тела вращения» |
|
|
| ОБ АКСИОМАХ ПЛАНИМЕТРИИ | 2 |
|
-
| Об аксиомах планиметрии. |
|
|
-
| Об аксиомах планиметрии. |
|
|
| Итоговое повторение | 7 |
|
-
| Признаки равенства треугольников . Решение задач. |
|
|
-
| Признаки и свойства параллельных прямых. Решение задач. |
|
|
-
| Соотношение между сторонами и углами треугольника. Решение задач. |
|
|
-
| Итоговая контрольная работа. |
|
|
-
| Параллелограмм. Прямоугольник .Ромб. Квадрат. Решение задач. |
|
|
-
| Признаки подобия треугольников. Решение задач. |
|
|
-
| Окружность. Решение задач. |
|
|
6. СРЕДСТВА КОНТРОЛЯ
В ходе реализации данной программы предусмотрены следующие виды и формы контроля: самостоятельные работы, тестирование, математические диктанты, контрольные работы. Формы учёта достижений это: проверка тетрадей по предмету, анализ текущей успеваемости, внеурочная деятельность- участие в олимпиадах, математических конкурсах.
7. УЧЕБНО – МЕТОДИЧЕСКИЕ СРЕДСТВА ОБУЧЕНИЯ .
Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б., Позняк Э. Г., Юдина И. И. Геометрия 7-9. – М.: Просвещение, 2008.
Атанасян Л.С., Бутузов В.Ф. Изучение геометрии в 7-9 классах. - М.: Просвещение, 2003.
Гаврилова Н.Ф.. Поурочные разработки по геометрии 8 класс. – М: ВАКО, 2005.
Звавич Л.И. и другие. Контрольные и проверочные работы по геометрии 7-9 классы. - М.: Дрофа, 2001г.
Зив Б.Г., Меллер В.М. Дидактические материалы по геометрии. - М.: Просвещение, 1999г.
Зив Б.Г. Меллер В.М..Бакинский А.Г. Задачи по геометрии для 7-11классов. - М.: Просвещение, 1991г.
Мельникова Н.Б. Геометрия: Дидактические материалы для 7-9 кл. общеобразоват. учреждений. – М.: Мнемозина, 1999.
Кукарцева Г.И. Сборник задач по геометрии в рисунках и тестах. 7-9 классы. - М.: Мнемозина, 1997г
Саврасов С.М., Ястребинецкий Г.А.. Упражнения по планиметрии на готовых чертежах.- М.: Просвещение, 1987г.
Примерная программа основного общего образования по математике 2005г. (сборник нормативных документов. Математика / сост. Э.Д. Днепров, А.Г Аркадьев. – 2-е изд., стереотип. – М.: Дрофа, 2008),
Программы общеобразовательных учреждений. Геометрия. 7 – 9 классы./сост. Бурмистрова Т. А. – М: «Просвещение», 2008
Стандарт основного общего образования по математике//«Вестник образования» -2004 - № 12

 Получите свидетельство
Получите свидетельство Вход
Вход











 Рабочая программа по геометрии (9 класс) (0.23 MB)
Рабочая программа по геометрии (9 класс) (0.23 MB)
 0
0 457
457 107
107 Нравится
0
Нравится
0






