Муниципальное бюджетное образовательное учреждение
Средняя общеобразовательная школа № 33 имени
Героя Советского Союза Л.П. Тихмянова
УТВЕРЖДАЮ
Директор МБОУ - СОШ № 33
_____________ Н.Н. Акулова
приказ _______от ______2012 года
РАБОЧАЯ ПРОГРАММА
по геометрии
в 8 « Б » классе
2012 – 2013 учебный год
Составитель программы:
учитель математики
Панина Елена Юрьевна
Программа рассмотрена на заседании школьного методического объединения
Протокол № __ от «__»_________2012г.
Руководитель__________________________( _______ __________)
1.ПОЯСНИТЕЛЬНАЯ ЗАПИСКА.
Нормативно-правовая база.
Данная рабочая программа ориентирована на учащихся 8 классов и реализуется на основе следующих документов:
1.Закон РФ «Об образовании», п.7,ст.32;
2. Письмо Департамента образования от 13.11.2002 г. «»О развитии содержания
общего образования.
3.Программа для общеобразовательных школ, гимназий, лицеев:
Сборник “Программы для общеобразовательных школ, гимназий, лицеев:
Математика. 5-11 кл.”/ Сост. Г.М.Кузнецова, Н.Г. Миндюк. – 3-е изд., стереотип.-
М. Дрофа, 2002; 4-е изд. – 2004г.
4.Стандарт основного общего образования по математике.
Стандарт основного общего образования по математике //Математика в школе. –
2004г,-№4, -с.4
5.Федерального перечня учебников, рекомендованных Министерством образования
Российской Федерации к использованию в образовательном процессе в
общеобразовательных учреждениях на 2012-2013 учебный год,
Программы по геометрии к учебнику 7-9. Автор Атанасян Л.С., В. Ф. Бутузов, С. Б. Кадомцев и др.(Составитель программ: Т. А .Бурмистрова. «Просвещение», 2008 г. )
Учебно-методического комплекта «Геометрия, 7–9», авторы Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др.
Данная рабочая программа ориентирована на учащихся 8классов, соответствует учебнику «геометрия 7-9». Автор Атанасян Л.С., В. Ф. Бутузов, С. Б. Кадомцев и др.8 г.
1.2 Место предмета в федеральном базисном учебном плане.
В соответствии с базисным учебным планом и учебным планом МБОУ –СОШ №33 г. Тулы в 8 классе на изучение курса «Геометрия» отводится 2 часа в неделю, 34 учебных недель т.е. 68 часов в год. Распределение часов по разделам курса произведено в соответствии с авторской программой.
Причины создания рабочей программы.
Распределение часов по разделам курса произведено в соответствии с авторской программой.
1.4 Общая характеристика учебного предмета.
В курсе геометрии 8 класса изучаются наиболее важные виды четырехугольников -параллелограмм, прямоугольник, ромб, квадрат, трапеция; даётся представление о фигурах, обладающих осевой или центральной симметрией; расширяются и углубляются полученные в 5—6 классах представления обучающихся об измерении и вычислении площадей; выводятся формулы площадей прямоугольника, параллелограмма, треугольника, трапеции; доказывается одна из главных теорем геометрии — теорему Пифагора; вводится понятие подобных треугольников; рассматриваются признаки подобия треугольников и их применения; делается первый шаг в освоении учащимися тригонометрического аппарата геометрии; расширяются сведения об окружности, полученные учащимися в 7 классе; изучаются новые факты, связанные с окружностью; знакомятся обучающиеся с четырьмя замечательными точками треугольника; знакомятся обучающиеся с выполнением действий над векторами как направленными отрезками, что важно для применения векторов в физике.
Изучение программного материала дает возможность учащимся:
осознать, что геометрические формы являются идеализированными образами реальных объектов;
научиться использовать геометрический язык для описания предметов окружающего мира;
получить представления о некоторых областях применения геометрии в быту, науке, технике, искусстве;
усвоить систематизированные сведения о плоских фигурах и основных геометрических отношениях;
приобрести опыт дедуктивных рассуждений: уметь доказывать основные теоремы курса, проводить доказательные рассуждения в ходе решения задач;
научиться решать задачи на доказательство, вычисление и построение;
овладеть набором эвристик, часто применяемых при решении планиметрических задач на вычисление и доказательство (выделение ключевой фигуры, стандартное дополнительное построение, геометрическое место точек и т. п.);
приобрести опыт применения аналитического аппарат (алгебраические уравнения и др.) для решения геометрических задач.
1.5 Цели обучения.
Цели обучения математики в общеобразовательной школе определяются ее ролью в развитии общества в целом и формировании личности каждого отдельного человека. Программа направлена на достижение следующих целей:
овладение системой математических знаний и умений, необходимых для применения практической деятельности изучения смежных дисциплин, продолжения образования;
интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, пространственных представлений;
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
воспитание культуры личности, отношения к математике как части общечеловеческой культуры, понимание значимости математики для научно технического прогресса;
развитие представлений о полной картине мира, о взаимосвязи математики с другими предметами.
В курсе геометрии 8-го класса продолжается решение задач на признаки равенства треугольников, но в совокупности с применением новых теоретических факторов. Теореме о сумме углов выпуклого многоугольника позволяет расширить класс задач. Формируется практические навыки вычисления площадей многоугольников в ходе решения задач. Особое внимание уделяется применению подобия треугольников к доказательствам теорем и решению задач. Даются первые знания о синусе, косинусе и тангенсе острого угла прямоугольного треугольника. Даются учащимся систематизированные сведения об окружности и её свойствах, вписанной и описанной окружностях. Серьезное внимание уделяется формированию умений рассуждать, делать простые доказательства, давать обоснования выполняемых действий. Параллельно закладываются основы для изучения систематических курсов стереометрии, физики, химии и других смежных предметов.
Задачи:
систематизировать знания обучающихся об основных свойствах простейших геометрических фигур;
изучить признаки равенства треугольников;
сформировать умение доказывать равенство треугольников с опорой на признаки равенства треугольников;
дать систематизированные сведения о параллельности прямых;
расширить знания обучающихся о треугольниках;
систематизировать и расширить знания обучающихся о свойствах окружности;
сформировать умение решать простейшие задачи на построение с помощью циркуля и линейки.
1.6 Структура рабочей программы.
Рабочая программа включает следующие разделы:
пояснительную записку;
основное содержание;
примерное распределение учебных часов по разделам программы;
требования к уровню подготовки учащихся данного класса;
тематическое планирование учебного материала;
поурочное планирование;
примерные контрольные работы;
учебное и учебно-методическое обеспечение обучения.
1.7 Обоснование увеличения/ уменьшения часов.
Распределение часов по разделам курса произведено в соответствии с авторской программой.
1.8 Формы и методы обучения.
Основной формой организации учебного процесса является классно-урочная система. В качестве дополнительных форм организации образовательного процесса по данной программе используется система консультационной поддержки, индивидуальных занятий, работа учащихся с использованием современных информационных технологий: игровое моделирование (дидактические игры, работа в малых группах, работа в парах сменного состава); проблемное обучение; личностно ориентированное обучение.
Теоретический материал курса излагается на наглядно-интуитивном уровне, математические методы и законы формулируются в виде правил. Курс строится на индуктивной основе с привлечением дедуктивных рассуждений.
Учебный процесс ориентирован на:
создание оптимальных условий обучения;
исключение психотравмирующих факторов;
сохранение психосоматического состояния здоровья учащихся;
развитие положительной мотивации к освоению программы;
развитие индивидуальности и одаренности каждого ребенка.
рациональное сочетание устных и письменных видов работы как при изучении теории, так и при решении задач;
сбалансированное сочетание традиционных и новых методов обучения;
оптимизированное применение объяснительно-иллюстративных и эвристических методов;
использование современных технических средств обучения.
2.ТРЕБОВАНИЯ К УРОВНЮ ПОДГОТОВКИ УЧАЩИХСЯ.
1. Уметь объяснить, какая фигура называется многоугольником, назвать его элементы; знать, что такое периметр многоугольника, какой многоугольник называется выпуклым; уметь вывести формулу суммы углов выпуклого многоугольника .Уметь находить углы многоугольников, их периметры.
2. Знать определения параллелограмма и трапеции, виды трапеций, формулировки свойств и признаков параллелограмма и равнобедренной трапеции, уметь их доказывать и применять при решении задач. Уметь выполнять деление отрезка на n равных частей с помощью циркуля и линейки; используя свойства параллелограмма и равнобедренной трапеции уметь доказывать некоторые утверждения. Уметь выполнять задачи на построение четырехугольников.
3. Знать определения частных видов параллелограмма: прямоугольника, ромба и квадрата, формулировки их свойств и признаков.
4. Знать определения симметричных точек и фигур относительно прямой и точки.
Уметь строить симметричные точки и распознавать фигуры, обладающие осевой симметрией и центральной симметрией.
5. Знать основные свойства площадей и формулу для вычисления площади прямоугольника. Уметь вывести формулу для вычисления площади прямоугольника и использовать ее при решении задач.
6. Знать формулы для вычисления площадей параллелограмма, треугольника и трапеции; уметь их доказывать, а также знать теорему об отношении площадей треугольников, имеющих по равному углу.
7. Знать теорему Пифагора и обратную ей теорему, область применения, пифагоровы тройки. Уметь находить неизвестную величину в прямоугольном треугольнике.
8. Знать определения пропорциональных отрезков и подобных треугольников, теорему об отношении подобных треугольников и свойство биссектрисы треугольника .Уметь определять подобные треугольники, находить неизвестные величины из пропорциональных отношений.
9. Знать признаки подобия треугольников, определение пропорциональных отрезков. Уметь доказывать признаки подобия и применять их при решении задач .
Знать теоремы о средней линии треугольника, точке пересечения медиан треугольника и пропорциональных отрезках в прямоугольном треугольнике. Уметь доказывать эти теоремы и применять при решении задач типа 567, 568, 570, 572 – 577, а также уметь с помощью циркуля и линейки делить отрезок в данном отношении и решать задачи на построение типа 586 – 590.
Знать определения синуса, косинуса и тангенса острого угла прямоугольного треугольника, значения синуса, косинуса и тангенса для углов 30, 45 и 60, метрические соотношения. Уметь доказывать основное тригонометрическое тождество, решать задачи типа 591 – 602.
Знать возможные случаи взаимного расположения прямой и окружности, определение касательной, свойство и признак касательной. Уметь их доказывать и применять при решении задач типа 631, 633 – 636, 638 – 643, 648, выполнять задачи на построение окружностей и касательных, определять отрезки хорд окружностей.
Знать, какой угол называется центральным и какой вписанным, как определяется градусная мера дуги
Знать теоремы о биссектрисе угла и о серединном перпендикуляре к отрезку, их следствия, а также теорему о пересечении высот треугольника. Уметь доказывать эти теоремы и применять их при решении задач типа 674 – 679, 682 – 686. Уметь выполнять построение замечательных точек треугольника.
Знать, какая окружность называется вписанной в многоугольник и какая описанной около многоугольника, теоремы об окружности, вписанной в треугольник, и об окружности, описанной около треугольника, свойства вписанного и описанного четырехугольников. Уметь доказывать эти теоремы и применять при решении задач типа 689 – 696, 701 – 711.
Знать определения вектора и равных векторов. Уметь изображать и обозначать векторы, откладывать от данной точки вектор, равный данному, решать задачи типа 741 – 743, 745 – 752.
Знать законы сложения векторов, определение разности двух векторов; знать, какой вектор называется противоположным данному; уметь объяснить, как определяется сумма двух и более векторов; уметь строить сумму двух и более данных векторов, пользуясь правилами треугольника, параллелограмма, многоугольника, строить разность двух данных векторов двумя способами, решать задачи типа 759 – 771.
Знать, какой вектор называется произведением вектора на число, какой отрезок называется средней линией трапеции. Уметь формулировать свойства умножения вектора на число, формулировать и доказывать теорему о средней линии трапеции.
Уметь применять все изученные формулы при решении задач, в устной форме доказывать теоремы и излагать необходимый теоретический материал.
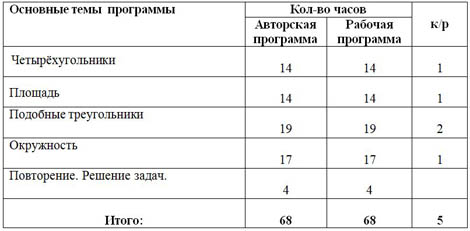
3.УЧЕБНО - ТЕМАТИЧЕСКИЙ ПЛАН.
Рабочая программа не отличается от авторской по содержанию тем образовательного стандарта и рекомендуемой последовательности тем учебного курса.
| Основные темы программы | Кол-во часов |
к/р |
| Авторская программа | Рабочая программа |
| Четырёхугольники |
14 |
14 |
1 |
|
Площадь |
14 |
14 |
1 |
| Подобные треугольники |
19 |
19 |
2 |
| Окружность |
17 |
17 |
1 |
| Повторение. Решение задач. |
4 |
4 |
|
|
Итого: |
68 |
68 |
5 |
4. СОДЕРЖАНИЕ ПРОГРАММЫ УЧЕБНОГО КУРСА.
Глава 5. Четырехугольники (14 часов)
Многоугольник, выпуклый многоугольник, четырехугольник. Параллелограмм, его свойства и признаки. Трапеция. Прямоугольник, ромб, квадрат, их свойства. Осевая и центральная симметрии.
Цель: изучить наиболее важные виды четырехугольников — параллелограмм, прямоугольник, ромб, квадрат, трапецию; дать представление о фигурах, обладающих осевой или центральной симметрией.
Доказательства большинства теорем данной темы и решения многих задач проводятся с помощью признаков равенства треугольников, поэтому полезно их повторить, в начале изучения темы.
Осевая и центральная симметрии вводятся не как преобразование плоскости, а как свойства геометрических фигур, в частности четырехугольников. Рассмотрение этих понятий как движений плоскости состоится в 9 классе.
Глава 6. Площадь (14 часов)
Понятие площади многоугольника. Площади прямоугольника, параллелограмма, треугольника, трапеции. Теорема Пифагора.
Цель: расширить и углубить полученные в 5—6 классах представления обучающихся об измерении и вычислении площадей; вывести формулы площадей прямоугольника, параллелограмма, треугольника, трапеции; доказать одну из главных теорем геометрии — теорему Пифагора.
Вывод формул для вычисления площадей прямоугольника, параллелограмма, треугольника, трапеции основывается на двух основных свойствах площадей, которые принимаются исходя из наглядных представлений, а также на формуле площади квадрата, обоснование которой не является обязательным для обучающихся.
Нетрадиционной для школьного курса является теорема об отношении площадей треугольников, имеющих по равному углу. Она позволяет в дальнейшем дать простое доказательство признаков подобия треугольников.
В этом состоит одно из преимуществ, обусловленных ранним введением понятия площади. Доказательство теоремы Пифагора основывается на свойствах площадей и формулах для площадей квадрата и прямоугольника. Доказывается также теорема, обратная теореме Пифагора.
Глава 7. Подобные треугольники (19 часов)
Подобные треугольники. Признаки подобия треугольников. Применение подобия к доказательству теорем и решению задач. Синус, косинус и тангенс острого угла прямоугольного треугольника.
Цель: ввести понятие подобных треугольников; рассмотреть признаки подобия треугольников и их применения; сделать первый шаг в освоении учащимися тригонометрического аппарата геометрии.
Определение подобных треугольников дается не на основе преобразования подобия, а через равенство углов и пропорциональность сходственных сторон.
Признаки подобия треугольников доказываются с помощью теоремы об отношении площадей треугольников, имеющих по равному углу.
На основе признаков подобия доказывается теорема о средней линии треугольника, утверждение о точке пересечения медиан треугольника, а также два утверждения о пропорциональных отрезках в прямоугольном треугольнике. Дается представление о методе подобия в задачах на построение.
В заключение темы вводятся элементы тригонометрии — синус, косинус и тангенс острого угла прямоугольного треугольника.
Глава 8. Окружность (17 часов)
Взаимное расположение прямой и окружности. Касательная к окружности, ее свойство и признак. Центральные и вписанные углы. Четыре замечательные точки треугольника. Вписанная и описанная окружности.
Цель: расширить сведения об окружности, полученные учащимися в 7 классе; изучить новые факты, связанные с окружностью; познакомить обучающихся с четырьмя замечательными точками треугольника.
В данной теме вводится много новых понятий и рассматривается много утверждений, связанных с окружностью. Для их усвоения следует уделить большое внимание решению задач. Утверждения о точке пересечения биссектрис треугольника и точке пересечения серединных перпендикуляров к сторонам треугольника выводятся как следствия из теорем о свойствах биссектрисы угла и серединного перпендикуляра к отрезку. Теорема о точке пересечения высот треугольника (или их продолжений) доказывается с помощью утверждения о точке пересечения серединных перпендикуляров.
Наряду с теоремами об окружностях, вписанной в треугольник и описанной около него, рассматриваются свойство сторон описанного четырехугольника и свойство углов вписанного четырехугольника.
9. Повторение. Решение задач. (4 часа)
Цель: Повторение, обобщение и систематизация знаний, умений и навыков за курс геометрии 8 класса.
КАЛЕНДАРНО ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ
ПО ГЕОМЕТРИИ В 8 КЛАССЕ
Класс: 8 «Б»
Годовое количество часов: 68
Количество часов в неделю: 2
Плановое количество контрольных работ: 5
Iч - 1
IIч - 1
IIIч - 2
IVч – 1
| № урока | Содержание материала | Кол-во часов | Сроки проведения |
| Глава V. Четырехугольники. | 14 |
|
|
| 1.1. Многоугольники. | 2 |
|
-
| Понятие многоугольника. выпуклого многоугольника. | 1 |
|
-
| Понятие четырехугольника. | 1 |
|
|
| 1.2. Параллелограмм и трапеция. | 5 |
|
-
| Определение параллелограмма. | 1 |
|
-
| Свойства параллелограмма. | 1 |
|
-
| Признаки параллелограмма. | 1 |
|
-
| Решение задач по теме «Параллелограмм». | 1 |
|
-
| Трапеция. Виды трапеции. | 1 |
|
|
| 1.3. Прямоугольник, ромб, квадрат. | 7 |
|
-
| Прямоугольник и его свойства. | 1 |
|
-
| Ромб и его свойства. | 1 |
|
-
| Квадрат и его свойства. | 1 |
|
-
| Осевая и центральная симметрия. | 1 |
|
-
| Зачет №1 по теме «Четырехугольники» | 1 |
|
-
| Решение задач по теме «Четырехугольники» | 1 |
|
-
| Контрольная работа №1 по теме «Четырехугольники» | 1 |
|
| Глава VΙ. Площади фигур. | 14 |
|
|
| 2.1. Площадь многоугольника | 2 |
|
-
| Понятие площади многоугольника. | 1 |
|
-
| Площадь прямоугольника. | 1 |
|
|
| 2.2. Площадь параллелограмма, треугольника и трапеции | 6 |
|
-
| Площадь параллелограмма. | 1 |
|
-
| Решение задач по теме «Площадь параллелограмма». | 1 |
|
-
| Площадь треугольника. | 1 |
|
-
| Решение задач по теме «Площадь треугольника». | 1 |
|
-
| Площадь трапеции. | 1 |
|
-
| Решение задач по теме «Площадь трапеции». | 1 |
|
|
| 2.3. Теорема Пифагора. | 6 |
|
-
| Теорема Пифагора. | 1 |
|
-
| Решение задач на применение теоремы Пифагора. | 1 |
|
-
| Теорема обратная теореме Пифагора. | 1 |
|
-
| Зачет №2 по теме «Площадь». |
|
|
| Решение задач по теме «Площадь параллелограмма». | 1 |
|
-
| Контрольная работа №2 по теме «Площадь». | 1 |
|
| Глава 3. Подобные треугольники | 19 |
|
|
| 3.1. Определение подобных треугольников. | 2 |
|
-
| Пропорциональные отрезки. Определение подобных треугольников. | 1 |
|
-
| Отношение площадей подобных треугольников. | 1 |
|
|
| 3.2. Признаки подобия треугольников. | 6 |
|
-
| Первый признак подобия треугольников. | 1 |
|
-
| Решение задач на применение первого признака подобия. | 1 |
|
-
| Второй признак подобия треугольников. | 1 |
|
-
| Решение задач на применение второго признака подобия. | 1 |
|
-
| Третий признак подобия треугольников. | 1 |
|
-
| Контрольная работа №3 по теме «Признаки подобия треугольников». | 1 |
|
|
| 3.3. Применение подобия к доказательству теорем и решению задач. | 6 |
|
-
| Средняя линия треугольника. | 1 |
|
-
| Решение задач по теме «Средняя линия треугольника». | 1 |
|
-
| Утверждение о точке пересечения медиан треугольника. | 1 |
|
-
| Пропорциональные отрезки в прямоугольном треугольнике. | 1 |
|
-
| Решение задач по теме «Пропорциональные отрезки в прямоугольном треугольнике». | 1 |
|
-
| Метод подобия в задачах на построение. О подобии произвольных фигур. | 1 |
|
|
| 3.4. Соотношения между сторонами и углами прямоугольного треугольника. | 4 |
|
-
| Синус, косинус, тангенс острого угла прямоугольного треугольника. | 1 |
|
-
| Основное тригонометрическое тождество. | 1 |
|
-
| Значение синуса, косинуса, тангенса для углов 30, 45, 60. | 1 |
|
-
| Зачет № 3 по теме «Применение подобия к решению задач». |
|
|
-
| Контрольная работа №4 по теме «Применение подобия к решению задач». | 1 |
|
| Глава 4. Окружность | 17 |
|
|
| 4.1. Касательная к окружности. | 3 |
|
-
| Взаимное расположение прямой и окружности. | 1 |
|
-
| Касательная к окружности. | 1 |
|
-
| Свойство отрезков касательных, проведенных из одной точки к окружности. | 1 |
|
|
| 4.2. Центральные и вписанные углы. | 3 |
|
-
| Градусная мера дуги окружности. Определение центрального угла. | 1 |
|
-
| Теорема о вписанном угле. Свойства вписанного угла. | 1 |
|
-
| Свойство двух пересекающихся хорд окружности. | 1 |
|
|
| 4.3. Четыре замечательные точки треугольника. | 3 |
|
-
| Свойство биссектрисы угла. | 1 |
|
-
| Свойство серединного перпендикуляра к отрезку. | 1 |
|
-
| Теорема о пересечении высот треугольника. | 1 |
|
|
| 4.4. Вписанная и описанная окружности. | 7 |
|
-
| Вписанная окружность. | 1 |
|
-
| Теорема об окружности, вписанной в треугольник. | 1 |
|
-
| Описанная окружность. | 1 |
|
-
| Теорема об окружности, описанной около треугольника. | 1 |
|
-
| Окружность вписанная в четырехугольник и описанная около четырехугольника. | 1 |
|
-
| Решение задач по теме « Окружность». | 1 |
|
-
| Зачет № 4 по теме « Окружность». |
|
|
-
| Контрольная работа №5 по теме « Окружность». | 1 |
|
| Повторение. Решение задач. | 4 |
|
-
| Решение задач по теме «Площадь треугольника». | 1 |
|
-
| Решение задач по теме «Площадь параллелограмма». | 1 |
|
-
| Решение задач по теме «Подобные треугольники». | 1 |
|
-
| Решение задач по теме «Окружность». | 1 |
|
6. СРЕДСТВА КОНТРОЛЯ
В ходе реализации данной программы предусмотрены следующие виды и формы контроля: самостоятельные работы, тестирование, математические диктанты, контрольные работы. Формы учёта достижений это: проверка тетрадей по предмету, анализ текущей успеваемости, внеурочная деятельность- участие в олимпиадах, математических конкурсах.
7. УЧЕБНО – МЕТОДИЧЕСКИЕ СРЕДСТВА ОБУЧЕНИЯ .
Учебник: Атанасян Л.С., Бутузов В.Ф. и др. Геометрии: 7-9 класс.-М.: Просвещение, 2005-2008.;
Самостоятельные и контрольные работы по алгебре и геометрии для 7класса.-М.: Илекса, Харьков: Гимназия, 1999.
Математические диктанты 7-11 классыМ.: Илекса2005 г.;
«Примерное планирование учебного материала и контрольные работы по математике в 5-9 классах»;В.И. Жохов, Картышева Г.Д.
Упражнения по планиметрии на готовых чертежах Саврасова С.М., Ястребинецкий Г.А.: Пособие для учителя. – М. : Просвещение, 1987. – 112 с.

 Получите свидетельство
Получите свидетельство Вход
Вход











 Рабочая программа по геометрии (8 класс) (42.25 КB)
Рабочая программа по геометрии (8 класс) (42.25 КB)
 0
0 694
694 46
46 Нравится
0
Нравится
0


