Рабочая программа по геометрии (10 класс)

Пояснительная записка

На основании статьи 47 пункта 3 закона «Об образовании» (новый), на основании статьи 32 пункта 2 закона «Об образовании» (старый), в соответствии с федеральным компонентом государственного стандарта общего образования одобренного решением коллегии Минобразования России и Президиума Российской академии образования от 23 декабря 2003 года №21/12, утвержденного приказом Минобразования России «Об утверждении федерального компонента государственных стандартов начального общего, основного общего и среднего (полного) общего образования» от 5 марта 2004 года №1089, федерального базисного учебного плана и примерных учебных планов, одобренных решением коллегии Минобразования России и Президиума Российской академии образования от 23 декабря 2003 года №21/12, утвержденных приказом Минобразования России «Об утверждении федерального базисного плана учебного плана  начального общего, основного общего и среднего (полного) общего образования» от 9 марта 2004 года №1312, примерной программы основного общего образования по математике, на основании утвержденного федерального перечня учебников, рекомендованных (допущенных) к использованию в образовательном процессе в образовательных учреждениях, реализующих образовательные программы общего образования и имеющих государственную аккредитацию, на 2013/2014 учебный год составлена данная рабочая программа по геометрии.

Рабочая программа по геометрии составлена на основе нормативных документов:

Государственный образовательный стандарт основного общего и среднего (полного) общего образования;

Закон РФ «Об образовании» [Электронный ресурс] – Российская газета.

Закон РФ «Об образовании» [Электронный ресурс] – Российская газета.

Приказ Минобрнауки России от 19.12.2012 № 1067 «Об утверждении федеральных перечней учебников, рекомендованных (допущенных) к использованию в образовательном процессе в образовательных учреждениях, реализующих образовательные программы общего образования и имеющих государственную аккредитацию, на 2013 / 2014 учебный год» [Электронный ресурс] – Российская газета.

Обязательный минимум содержания основного общего курса математики;

Примерная основная образовательная программа образовательного учреждения. Основная школа / сост. Е. С. Савинов — М.: Просвещение, 2011;

Программы для общеобразовательных школ, гимназий, лицеев. Математика. «Дрофа». Москва. 2004. С. 172-174.

Сборник нормативных документов. Математика/ сост. Э.Д. Днепров, А.Г. Аркадьев  «Дрофа». Москва. 2009

Региональный компонент

Федеральный базисный учебный план для образовательных учреждений РФ от 09.03.2004 № 1312.

Рабочая программа предназначена для работы  в 10классе  по учебнику

«Геометрия 10-11», И. Ф. Шарыгин и др., Дрофа, 2013. Курс рассчитан на 66 часов в год (по 2 часа в неделю).

Программа  конкретизирует содержание предметных тем образовательного стандарта и дает примерное распределение учебных часов по разделам курса.

В данном курсе представлены следующие со­держательные линии: «Прямые и плоскости в пространстве», «Многогранники», «Тела и по­верхности вращения», «Объемы тел и площади поверхностей», «Координаты и векторы».

В рамках указанных содержательных линий решаются следующие задачи:

систематизация полученных сведений о плоских геометрических фигурах;

совершенствование навыков изображения плоских и пространственных фигур; расширение и совершенствование геометрического аппарата, сформированного на ступени основного общего об­разования, и его применение к решению геомет­рических задач;

расширение и систематизация общих све­дений о геометрических телах.

Изучение геометрии в старшей школе на базо­вом уровне направлено на достижение следующих целей:

формирование представлений о геометрии как особом языке науки, средстве моделирования явлений, об идеях и методах геометрии;

развитие логического мышления, про­странственного воображения, критичности мыш­ления, необходимом для будущей профессиональ­ной деятельности, а также для обучения в вузе;

овладение знаниями и умениями, необхо­димыми в повседневной жизни, для изучения дру­гих школьных предметов на базовом уровне; для получения образования, не требующего усилен­ной математической подготовки;

воспитание общей культуры личности, по­нимание значимости идей и методов геометрии для науки и культуры.

Компетенции изучения курса

Программа предполагает достижение выпускниками старшей школы следующих личностных, метапредметных и предметных результатов.

В личностных результатах сформированность:

целостного мировоззрения, соответствующего совре­менному уровню развития науки математики и общественной практики ее применения;

основ саморазвития и самовоспитания в соответствии с общечеловеческими ценностями и идеалами гражданского общества; готовности и способности к самостоятельной, творческой и ответственной деятельности с применением ме­тодов математики.

Весь материал - в документе.

Пояснительная записка

На основании статьи 47 пункта 3 закона «Об образовании» (новый), на основании статьи 32 пункта 2 закона «Об образовании» (старый), в соответствии с федеральным компонентом государственного стандарта общего образования одобренного решением коллегии Минобразования России и Президиума Российской академии образования от 23 декабря 2003 года №21/12, утвержденного приказом Минобразования России «Об утверждении федерального компонента государственных стандартов начального общего, основного общего и среднего (полного) общего образования» от 5 марта 2004 года №1089, федерального базисного учебного плана и примерных учебных планов, одобренных решением коллегии Минобразования России и Президиума Российской академии образования от 23 декабря 2003 года №21/12, утвержденных приказом Минобразования России «Об утверждении федерального базисного плана учебного плана начального общего, основного общего и среднего (полного) общего образования» от 9 марта 2004 года №1312, примерной программы основного общего образования по математике, на основании утвержденного федерального перечня учебников, рекомендованных (допущенных) к использованию в образовательном процессе в образовательных учреждениях, реализующих образовательные программы общего образования и имеющих государственную аккредитацию, на 2013/2014 учебный год составлена данная рабочая программа по геометрии.

Рабочая программа по геометрии составлена на основе нормативных документов:

1. Государственный образовательный стандарт основного общего и среднего (полного) общего образования;

2. Закон РФ «Об образовании» [Электронный ресурс] // – Российская газета – URL: http://www.rg.ru/1992/07/31/obrazovanie-dok.html;

3. Закон РФ «Об образовании» [Электронный ресурс] // – Российская газета – URL: http://www.rg.ru/2012/12/30/obrazovanie-dok.html;

4. Приказ Минобрнауки России от 19.12.2012 № 1067 «Об утверждении федеральных перечней учебников, рекомендованных (допущенных) к использованию в образовательном процессе в образовательных учреждениях, реализующих образовательные программы общего образования и имеющих государственную аккредитацию, на 2013/2014 учебный год» [Электронный ресурс] // – Российская газета – URL: http://www.rg.ru/2013/02/08/uchebniki-dok.html;

5. Обязательный минимум содержания основного общего курса математики;

6. Примерная основная образовательная программа образовательного учреждения. Основная школа / сост. Е. С. Савинов — М.: Просвещение, 2011;

7. Программы для общеобразовательных школ, гимназий, лицеев. Математика. «Дрофа». Москва. 2004. С. 172-174.

8. Сборник нормативных документов. Математика/ сост. Э.Д. Днепров, А.Г. Аркадьев «Дрофа». Москва. 2009

9. Региональный компонент

10. Федеральный базисный учебный план для образовательных учреждений РФ от 09.03.2004 № 1312.

Рабочая программа предназначена для работы в 10классе по учебнику

«Геометрия 10-11», И. Ф. Шарыгин и др., Дрофа, 2013. Курс рассчитан на 66 часов в год (по 2 часа в неделю).

Программа конкретизирует содержание предметных тем образовательного стандарта и дает примерное распределение учебных часов по разделам курса.

В данном курсе представлены следующие со­держательные линии: «Прямые и плоскости в пространстве», «Многогранники», «Тела и по­верхности вращения», «Объемы тел и площади поверхностей», «Координаты и векторы».

В рамках указанных содержательных линий решаются следующие задачи:

• систематизация полученных сведений о плоских геометрических фигурах;

• совершенствование навыков изображения плоских и пространственных фигур; расширение и совершенствование геометрического аппарата, сформированного на ступени основного общего об­разования, и его применение к решению геомет­рических задач;

• расширение и систематизация общих све­дений о геометрических телах.

Изучение геометрии в старшей школе на базо­вом уровне направлено на достижение следующих целей:

• формирование представлений о геометрии как особом языке науки, средстве моделирования явлений, об идеях и методах геометрии;

• развитие логического мышления, про­странственного воображения, критичности мыш­ления, необходимом для будущей профессиональ­ной деятельности, а также для обучения в вузе;

• овладение знаниями и умениями, необхо­димыми в повседневной жизни, для изучения дру­гих школьных предметов на базовом уровне; для получения образования, не требующего усилен­ной математической подготовки;

• воспитание общей культуры личности, по­нимание значимости идей и методов геометрии для науки и культуры.

Компетенции изучения курса

Программа предполагает достижение выпускниками старшей школы следующих личностных, метапредметных и предметных результатов.

В личностных результатах сформированность:

• целостного мировоззрения, соответствующего совре­менному уровню развития науки математики и общественной практики ее применения;

• основ саморазвития и самовоспитания в соответствии с общечеловеческими ценностями и идеалами гражданского общества; готовности и способности к самостоятельной, творческой и ответственной деятельности с применением ме­тодов математики;

• готовности и способности к образованию, в том числе самообразованию, на протяжении всей жизни; сознательного отношения к непрерывному образованию как условию ус­пешной профессиональной и общественной деятельности на основе развитой мотивации учебной деятельности и личност­ного смысла изучения математики, заинтересованности в приобретении и расширении математических знаний и спо­собов действий, осознанности в построении индивидуальной образовательной траектории;

• осознанного выбора будущей профессии, ориентиро­ванной в применении математических методов и возможнос­тей реализации собственных жизненных планов; отношение к профессиональной деятельности как возможности участия в решении личных, общественных, государственных, общена­циональных проблем;

• логического мышления: критичности (умение распо­знавать логически некорректные высказывания), креативнос­ти (собственная аргументация, опровержения, постановка задач, формулировка проблем, работа над исследовательским проектом и др.).

В метапредметных результатах сформированность:

• способности самостоятельно ставить цели учебной и исследовательской, проектной деятельности, планировать, осуществлять, контролировать и оценивать учебные действия в соответствии с поставленной задачей и условиями ее выпол­нения;

• умения самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эф­фективные способы решения учебных и познавательных за­дач;

• умения находить необходимую информацию, критиче­ски оценивать и интерпретировать информацию в различных источниках (в справочниках, литературе, Интернете), пред­ставлять информацию в различной форме (словесной, таб­личной, графической, символической), обрабатывать, хра­нить и передавать информацию в соответствии с познаватель­ными или коммуникативными задачами;

• навыков осуществления познавательной, учебно-иссле­довательской и проектной деятельности, навыков разреше­ния проблем; способности и готовности к самостоятельному поиску методов решения практических задач, применению различных методов познания;

• умения продуктивно общаться и взаимодействовать в процессе совместной деятельности, учитывать позиции дру­гих участников деятельности, эффективно разрешать конф­ликты;

• умения владения языковыми средствами — умения яс­но, логично и точно излагать свою точку зрения, использо­вать адекватные языковые средства;

• умения представлять информацию в словесной, графи­ческой, табличной, символической форме;

навыков познавательной рефлексии как осознания со­вершаемых действий и мыслительных процессов, их результа- тов и оснований, границ своего знания и незнания, новых по­знавательных задач и средств их достижения.

В предметных результатах сформированность:

• представлений о геометрии как части мировой культу­ры и о ее месте в современной цивилизации, о способах опи­сания на математическом языке явлений реального мира;

• представлений об историческом пути развития геомет­рии как науки;

• представлений о математических понятиях как о важ­нейших математических моделях, позволяющих описывать и изучать разные процессы и явления; понимание возможности аксиоматического построения математических теорий;

• владение методами доказательств и алгоритмов реше­ния; умение их применять, проводить доказательные рассуж­дения в ходе решения задач;

• владение основными понятиями о плоских и простран­ственных геометрических фигурах, их основных свойствах;

• умения распознавать на чертежах, моделях и в реаль­ном мире геометрические фигуры;

• умения применять изученные свойства геометрических

• фигур и формулы для решения геометрических задач и задач с практическим содержанием;

• умения использовать готовые компьютерные програм­мы при решении задач.

СТРУКТУРА КУРСА

КОНТРОЛЬ РЕАЛИЗАЦИИ ПРОГРАММЫ

СТАРТОВЫЙ КОНТРОЛЬ:

Тест состоит из двух частей. Каждая часть включает пять задач. При выполнении заданий первой части учащимся нужно выбрать один из четырех предложенных ответов. При выполнении задач второй части учащиеся должны указать число, являющееся ответом задачи.

Часть 1

1. Какое утверждение верно для треугольника со сторонами 5, 9, 15?

а) треугольник остроугольный;

б) треугольник тупоугольный:

в) треугольник прямоугольный;

г) такого треугольника не существует.

2. Если одна из сторон треугольника на 3 см меньше другой стороны, высота делит третью сторону на отрезки 5 см и 10 см, то периметр треугольника равен:

а) 25см; б) 40 см;

в) 32см; г) 20 см.

3. Если один из углов ромба равен 60^º диагональ, проведенная из вершины этого утла, равна 4 см, то периметр ромба равен:

а) 16 см: б) 8 см;

в) 12 см: г) 24 см.

1. Величина одного углов треугольника равна 20°. Найдите величину острого угла между биссектрисами двух других углов треугольника

а) 84°; б) 92°;

в) 80°; в) 87°.

1. В Δ ABC сторона а = 7, сторона b = 8, сторона с = 5. Вычислите А

а) 120°; 6)45°;

в) 30°; в) 60°.

Часть II

1.В равнобедренном треугольнике боковая сторона делится точкой касания со вписанной окружностью в отношении 8:5, считая от вершины, лежащей против основания. Найдите основание треугольника, если радиус вписанной окружности равен 10.

2.В треугольнике ВСЕ 60º СЕ : ВС = 3: 1. Отрезок СК биссектриса треугольника. Найдите КЕ, если радиус описанной около треугольника окружности равен 8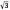 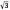см.

1. Найдите площадь треугольника КМР, если сторона КР равна 5, медиана РО равна 3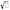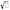2, КОР= 135°

2. Диагонали равнобедренной трапеции перпендикулярны. Найдите площадь трапеции, если ее средняя линия равна 5

3. Окружность, центр которой лежит на гипотенузе АВ прямоугольного треугольника ABC, касается катетов АС и ВС соответственно в точках Е и D. Найдите величину угла ABC (в градусах), если известно, что АЕ = 1, BD =3

ИТОГОВЫЙ КОНТРОЛЬ:

1. Основание конуса совпадает с одним из оснований цилиндра, а вершина конуса с центром другого ос­нования цилиндра. Во сколько раз площадь осево­го сечения цилиндра больше площади осевого сече­ния конуса?

2. Все ребра треугольной пирамиды равны 1. Рассмот­рите сечение этой пирамиды плоскостью, парал­лельной двум противоположным (скрещивающим­ся) ребрам пирамиды. Как называется многоуголь­ник, получившийся в сечении? Чему равен его периметр? В каких пределах меняется его пло­щадь?

3. Найдите радиус шара, касающегося трех граней единичного куба и вписанного в этот куб шара.

4. Отрезок, длина которого равна 1, образует угол в 45° с одной гранью прямого двугранного угла, и он же образует угол 30° с другой гранью этого же дву­гранного угла. Найдите длину проекции этого от­резка на ребро двугранного угла.

5. Высота пирамиды равна 1, все двугранные углы при основании равны 45°, периметр многоугольни­ка, расположенного в основании, равен 2р. Найди­те площадь этого многоугольника. При каких р та­кая пирамида возможна?

6. В основании треугольной пирамиды ABCD лежит правильный треугольник ABC. Найдите его сторо­ну, если известно, что все боковые грани этой пи­рамиды равновелики и BD = CD = 1, AD = 2.

ПЕРЕЧЕНЬ ПРОВЕРОЧНЫХ РАБОТ ПО МОДУЛЯМ

КОМПЛЕКТ ТЕОРЕТИЧЕСКИХ ВОПРОСОВ НА КОНЕЦ ГОДА

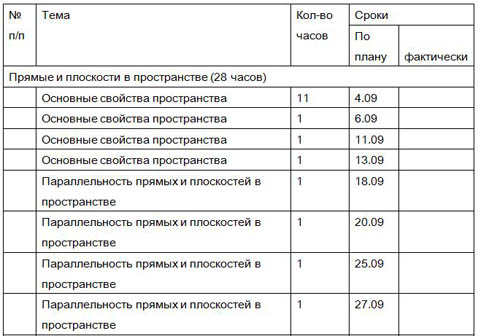
КАЛЕНДАРНО-ТЕМАТИЧЕСКИЙ ПЛАН

Планирование по модулям:

В результате изучения этой темы учащиеся должны

знать/понимать:

— содержание введенных свойств трехмерного пространства (аксиом стереометрии);

— что плоскость в пространстве можно задать:

а) тремя точками, не лежащими на одной прямой;

б) прямой и не принадлежащей ей точкой;

в) двумя пересекающимися прямыми;

г) двумя параллельными прямыми;

— случаи взаимного расположения прямых, плоскостей, а также прямых и плоскостей;

уметь:

— применять доказанные теоремы;

— видеть взаимное расположение прямых, прямых и плоскостей, плоскостей на моделях и изображениях многогранников;

— строить точки пересечения прямой и плоскости, изображать пересечения двух плоскостей;

— корректно обосновывать утверждения, возникающие при решении задач и доказательстве теорем.

В результате изучения этой темы учащиеся должны

знать/понимать:

— определения выпуклого многогранника и его элементов (вершины, ребра, грани, диагонали, двугранные и многогранные углы);

— определение прямоугольного параллелепипеда, куба, пирамиды;

— что куб — правильный прямоугольный параллелепипед;

— свойства диагоналей параллелепипеда;

— формулы вычисления площадей боковой и полной поверхностей пирамиды и призмы;

уметь:

— в параллельной проекции строить:

а) изображения куба, прямого и наклонного параллелепипедов, правильной пирамиды (правильного тетраэдра);

б) изображения прямых и плоскостей, параллельных и перпендикулярных ребрам и граням данного многогранника;

в) строить сечения многогранников;

г) на изображении многогранника выделять его невидимые элементы штриховыми линиями;

д) определять («видеть») и вычислять углы между его ребрами и гранями,

линейные углы двугранных углов между его гранями;

— строить методом следов, методом внутреннего проектирования, комбинированным методом сечения призмы и параллелепипеда и вычислять площади этих сечений.

В результате изучения этой темы учащиеся должны

знать/понимать:

— определения цилиндра, конуса, шара, сферы и их элементов;

уметь:

— применять формулы для вычисления площади боковой и полной поверхностей цилиндра и конуса;

— строить изображения цилиндра, конуса, шара, сферы и их сечения.

В результате изучения этой темы учащиеся должны

знать/понимать:

— что такое проектирование, сечение, угол между скрещивающимися прямыми;

уметь:

— находить угол и расстояние между скрещивающимися прямыми;

— изображать сечения тел вращения и многогранников;

— изображать развертки куба и тетраэдра.

МАТЕРИАЛЬНО-ТЕХНИЧЕСКОЕ ОБЕСПЕЧЕНИЕ

1. Компьютер

2. Компьютерные презентации

Приложения к рабочей программе

Приложение 1

График промежуточного контроля:

Приложения 2

Примерные контрольные работы

Контрольная работа № 1 «Прямые и плоскости в пространстве»

Вариант 1

1. В треугольнике ABC известны ВАС = 40°, ВСА = 25°. ВСКМ — трапеция с основаниями ВС и КМ, не лежащая в плоскости треугольника ABC. Каки­ми являются прямые АВ и КМ? Чему равен угол между ними?

2. Дана треугольная пирамида ABCD. На AD взята точка К так, что АК = 3KD, на АС — точка М так, что 2AM = 3МС. Через К и М проведена плоскость, параллельная АВ и пересекающая прямые BD и ВС в точках Р и Q соответственно. Найдите: 1) MQ : АВ; 2)КР :АВ; 3)KP : MQ.

Вариант 2

1. В треугольнике ABC известны BCPQ — трапеция, не лежащая в плоскости данного треугольника. ВС и PQ — основания тра­пеции. Какими являются прямые АВ и PQ? Чему равен угол между ними?

2. В треугольной пирамиде ABCD на BD взята точка K так, что ВК : KD = 2 : 1, на ВС — точка М так, что ВМ : МС = 3:4. Через К и М проведена плос­кость, пересекающая прямую AD в точке F, прямую АС — в точке F и параллельная АВ. Найдите

FK: АВ; 2) МТ :АВ; 3) FK : TМ.

Контрольная работа № 2 «Перпендикулярность прямой и плоскости»

Вариант 1

1. В пространстве отмечены четыре точки. Сколько может быть различных плоскостей, содержащих не менее трех из этих точек? (Перечислите все воз­можности.)

2. Дана треугольная пирамида ABCD. На прямой AD взята точка К так, что АК = 3KD, на АС — точка М так, что 2AM = 3МС. Через К и М проведена плоскость, параллельная АВ и пересекающая пря­мые BD и ВС в точках Р и Q соответственно. Най­дите MQ : КР.

3. Пусть ABCDE — правильный пятиугольник, ВСКМ — параллелограмм, не лежащий в плоскос­ти пятиугольника. Найдите угол между DE и КМ.

4. Задача из учебника (на усмотрение учителя).

5. В треугольнике ABC известны стороны: АВ = 5, ВС = 13, С А = 10. Проекции АВ и ВС на некоторую плоскость равны соответственно 4 и 12. Найдите длину проекции С А на эту же плоскость.

Вариант 2

1. 1.В пространстве имеется точка и две прямые. Сколь­ко может быть различных плоскостей, содержащих данную точку и хотя бы одну прямую? (Перечисли­те все возможности.)

2. 2.Дана треугольная пирамида ABCD. На AD взята точка К так, что ЗАК" = 5KD, на АС — точка М так, что AM = 5МС. Через К и М проведена плос­кость, параллельная АВ и пересекающая прямые BD и ВС в точках Р и Q соответственно. Найдите КР : MQ.

3. 3.Пусть KLMNP — правильный пятиугольник, АВКМ — параллелограмм, не принадлежащий плоскости этого пятиугольника. Чему равен угол между АВ и LN?

4. 4.Задача из учебника (на усмотрение учителя).

5. 5.В треугольнике две стороны равны 13 и 7, угол между ними 60°. Проекции данных сторон на неко­торую плоскость равны 12 и 4л/3. Найдите длину проекции третьей стороны на эту же плоскость.

Контрольная работа № 3 «Многогранники»

Вариант 1

1. В основании треугольной пирамиды лежит прямо­угольный треугольник с катетами 7 и 24 см. Боко­вые ребра образуют с высотой пирамиды углы, рав­ные 30°. Найдите боковые ребра.

2. Все ребра правильной треугольной призмы равны а. Найдите площадь сечения, проходящего через диа­гональ одной из ее граней и середину не принадле­жащего этой грани ребра.

3. В основании пирамиды лежит многоугольник с пе­риметром 2р, высота пирамиды равна h, двугран­ные углы при основании имеют величину а. Найди­те площадь основания.

4. Дан параллелепипед ABCDA₁B₁C₁D₁ Известно, что площадь треугольника BDA₁ равна S. Найдите пло­щадь сечения, проходящего через середины ребер A₁D₁ DC и BB₁

5. Сторона основания ABCD правильной четырех­угольной пирамиды ABCDE равна 2, боковые ребра равны 3. Боковая грань ABE служит основанием треугольной пирамиды ABEF, расположенной вне исходной пирамиды, причем AF = BF = 3, EF = 2. Сколько граней имеет многогранник ABCDEF? Как он называется? Через точку К на ребре EF такую, что ЕК = 1, проведена плоскость, перпендикулярная EF. Найдите площадь сечения.

Вариант 2

1. Боковые ребра треугольной пирамиды равны 2. В основании лежит треугольник, одна сторона ко­торого равна 3, а противолежащий угол равен 60°. Найдите высоту пирамиды.

2. Боковое ребро правильной треугольной призмы в два раза больше стороны основания. Проведено сечение через диагональ боковой грани призмы и середину противоположного ребра. Найдите наи­больший угол у получившегося в сечении треуголь­ника.

3. В основании пирамиды лежит многоугольник пло­щадью S и периметром Р. Все двугранные углы при основании равны (3. Найдите высоту пирамиды.

4. Дан параллелепипед ABCDA₁B₁C₁D₁. Известно, что площадь сечения, проходящего через середины АВ, АА_Х и AD, имеет площадь q. Найдите площадь се­чения, проходящего через середины ребер DD_V А₁В₁ и ВС.

5. Сторона основания ABCD правильной четырех­угольной пирамиды ABCDE равна 3, боковые ребра равны 4. Боковая грань ABE служит основанием треугольной пирамиды ABEF, расположенной вне исходной пирамиды, причем AF = BF = 4, EF = 3. Сколько граней имеет многогранник ABCDEF? Как он называется? Через точку К на ребре EF такую, что ЕК = 2, проведена плоскость, перпендикуляр­ная EF. Найдите площадь сечения.

Контрольная работа № 4 «Круглые тела»

Вариант 1

1. Найдите площадь сечения шара радиусом 4 см плоскостью, расстояние до которой от центра шара равно 3 см.

2. Расстояние от центра шара радиуса 3 до прямой l равно 2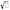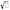3. Через l проведены две плоскости, ка­сающиеся шара. Найдите величину угла между этими плоскостями.

3. Найдите отношение радиуса описанного шара к ра­диусу вписанного шара для правильной треуголь­ной пирамиды, двугранные углы при основании ко­торой равны а.

4. В основании призмы лежит треугольник со сторо­нами 3, 4 и 5; боковые ребра этой призмы равны 12. Известно, что около этой призмы можно описать шар. Найдите радиус этого шара.

5. Радиус шара, вписанного в треугольную пирамиду, все ребра которой равны между собой, равен l. Найдите радиус шара, касающегося трех граней этой пирамиды и вписанного в нее шара.

Вариант 2

1. На каком расстоянии от центра шара радиуса 5 на­до провести плоскость, чтобы площадь получивше­гося сечения была в 3 раза меньше площади сече­ния, проходящего через центр шара?

2. Две плоскости пересекаются под углом 60°. Центр шара, касающегося обеих плоскостей, находится на расстоянии 5 см от линии их пересечения. Най­дите радиус этого шара, если известно, что этот ра­диус больше 3 см.

3. Найдите отношение радиуса описанного шара к ра­диусу вписанного шара для правильной шести­угольной пирамиды, двугранные углы при основа­нии которой равны а.

4. В основании прямой призмы лежит треугольник со сторонами 5, 12 и 13. Известно, что в эту призму можно вписать шар. Найдите радиус этого шара.

5. Все ребра треугольной пирамиды равны 1. Внутри пирамиды расположены два равных касающихся между собой шара. Найдите радиусы этих шаров, если известно, что каждый из них касается трех граней пирамиды, но при этом каждая грань каса­ется лишь одного шара.

Итоговая контрольная работа

1. Основание конуса совпадает с одним из оснований цилиндра, а вершина конуса с центром другого ос­нования цилиндра. Во сколько раз площадь осево­го сечения цилиндра больше площади осевого сече­ния конуса?

2. Все ребра треугольной пирамиды равны 1. Рассмот­рите сечение этой пирамиды плоскостью, парал­лельной двум противоположным (скрещивающим­ся) ребрам пирамиды. Как называется многоуголь­ник, получившийся в сечении? Чему равен его периметр? В каких пределах меняется его пло­щадь?

3. Найдите радиус шара, касающегося трех граней единичного куба и вписанного в этот куб шара.

4. Отрезок, длина которого равна 1, образует угол в 45° с одной гранью прямого двугранного угла, и он же образует угол 30° с другой гранью этого же дву­гранного угла. Найдите длину проекции этого от­резка на ребро двугранного угла.

5. Высота пирамиды равна 1, все двугранные углы при основании равны 45°, периметр многоугольни­ка, расположенного в основании, равен 2р. Найди­те площадь этого многоугольника. При каких р та­кая пирамида возможна?

6. В основании треугольной пирамиды ABCD лежит правильный треугольник ABC. Найдите его сторо­ну, если известно, что все боковые грани этой пи­рамиды равновелики и BD = CD = 1, AD = 2.

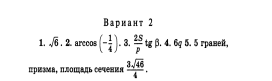
0