РАБОЧАЯ УЧЕБНАЯ ПРОГРАММА
ПО АЛГЕБРЕ
ДЛЯ 9 КЛАССА
СОСТАВИТЕЛЬ
ИЗЕКЕЕВА АЛИНА МИХАЙЛОВНА
УЧИТЕЛЬ ПЕРВОЙ
КВАЛИФИКАЦИОННОЙ КАТЕГОРИИ
Пояснительная записка к рабочей учебной программе
Рабочая программа учебного предмета «Алгебра» составлена в соответствии с требованиями федерального компонента государственного стандарта общего образования на основе типовой учебной программы (Программы общеобразовательных учреждений. Алгебра, 7-9 кл./Ш.А.Алимов, Ю.М.Колягин, С.В.Сидоров и др.; составитель Т.А. Бурмистрова. – М.: Просвещение, 2008, рекомендованной Министерством образования и науки РФ.)
Данная программа выполняет две основные функции.
Информационно-методическая функция позволяет всем участникам образовательного процесса получить представление о целях, содержании, общей стратегии обучения, воспитания и развития учащихся средствами данного учебного предмета.
Организационно-планирующая функция предусматривает выделение этапов обучения, структурирование учебного материала, определение его количественных и качественных характеристик на каждом из этапов, в том числе для содержательного наполнения промежуточной аттестации учащихся.
2. Общая характеристика учебного предмета
Математическое образование является обязательной и неотъемлемой частью общего образования на всех ступенях школы. Обучение математике в основной школе направлено на достижение следующих целей:
1) в направлении личностного развития:
• формирование представлений о математике как части общечеловеческой культуры, о значимости математики в развитии цивилизации и современного общества;
• развитие логического и критического мышления, культуры речи, способности к умственному эксперименту;
• формирование интеллектуальной честности и объективности, способности к преодолению мыслительных стереотипов, вытекающих из обыденного опыта;
• воспитание качеств личности, обеспечивающих социальную мобильность, способность принимать самостоятельные решения;
• формирование качеств мышления, необходимых для адаптации в современном информационном обществе;
• развитие интереса к математическому творчеству и математических способностей;
2) в метапредметном направлении:
• развитие представлений о математике как форме описания и методе познания действительности, создание условий для приобретения первоначального опыта математического моделирования;
• формирование общих способов интеллектуальной деятельности, характерных для математики и являющихся основой познавательной культуры, значимой для различных сфер человеческой деятельности;
3) в предметном направлении:
• овладение математическими знаниями и умениями, необходимыми для продолжения образования, изучения смежных дисциплин, применения в повседневной жизни;
• создание фундамента для математического развития, формирования механизмов мышления, характерных для математической деятельности.
Содержание раздела «Алгебра» направлено на формирование у учащихся математического аппарата для решения задач из разных разделов математики, смежных предметов, окружающей реальности. Язык алгебры подчеркивает значение математики как языка для построения математических моделей процессов и явлений реального мира. В задачи изучения алгебры входят также развитие алгоритмического мышления, необходимого, в частности, для усвоения курса информатики, овладения навыками дедуктивных рассуждений. Преобразование символьных форм вносит специфический вклад в развитие воображения учащихся, их способностей к математическому творчеству. В основной школе материал группируется вокруг рациональных выражений, а вопросы, связанные с иррациональными выражениями, с тригонометрическими функциями и преобразованиями, входят в содержание курса математики на старшей ступени обучения в школе.
Содержание раздела «Функции» нацелено на получение школьниками конкретных знаний о функции как важнейшей математической модели для описания и исследования разнообразных процессов. Изучение этого материала способствует развитию у учащихся умения использовать различные языки математики (словесный, символический, графический), вносит вклад в формирование представлений о роли математики в развитии цивилизации и культуры.
Раздел «Вероятность и статистика» — обязательный компонент школьного образования, усиливающий его прикладное и практическое значение. Этот материал необходим прежде всего для формирования у учащихся функциональной грамотности — умений воспринимать и критически анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей, проводить простейшие вероятностные расчеты. Изучение основ комбинаторики позволит учащимся рассматривать случаи, осуществлять перебор и подсчет числа вариантов, в том числе в простейших прикладных задачах.
При изучении статистики и вероятности расширяются представления о современной картине мира и методах его исследования, формируется понимание роли статистики как источника социально значимой информации и закладываются основы вероятностного мышления.
Место учебного предмета в учебном плане
На ступени основного общего образования на учебный предмет «Алгебра» отводится 315 часов согласно Федеральному базисному учебному плану для образовательных учреждений Российской Федерации, в том числе в 9 классе 105 часов (6 контрольных работ) из расчета 3-х учебных часов в неделю
Данная программа содержит все темы, включенные в федеральный компонент содержания образования.
При проведении уроков используются беседы, интегрированные уроки, практикумы, работа в группах, работа в парах, тестирование.
Итоговый промежуточный контроль проводится в форме Государственной итоговой аттестации (в новой форме).
4. Ценностные ориентиры содержания учебного предмета
Математическое образование играет важную роль как в практической, так и в духовной жизни общества. Практическая сторона математического образования связана с формированием способов деятельности, духовная — с интеллектуальным развитием человека, формированием характера и общей культуры.
Практическая полезность математики обусловлена тем, что ее предметом являются фундаментальные структуры реального мира: пространственные формы и количественные отношения — от простейших, усваиваемых в непосредственном опыте, до достаточно сложных, необходимых для развития научных и технологических идей. Без конкретных математических знаний затруднено понимание принципов устройства и использования современной техники, восприятие и интерпретация разнообразной социальной, экономической, политической информации, малоэффективна повседневная практическая деятельность. Каждому человеку в своей жизни приходится выполнять достаточно сложные расчеты, находить в справочниках нужные формулы и применять их, владеть практическими приемами геометрических измерений и построений, читать информацию, представленную в виду таблиц, диаграмм, графиков, понимать вероятностный характер случайных событий, составлять несложные алгоритмы и др.
Без базовой математической подготовки невозможно стать образованным современным человеком. В школе математика служит опорным предметом для изучения смежных дисциплин. В послешкольной жизни реальной необходимостью в наши дни является непрерывное образование, что требует полноценной базовой общеобразовательной подготовки, в том числе и математической. И наконец, все больше специальностей, где необходим высокий уровень образования, связано с непосредственным применением математики (экономика, бизнес, финансы, физика, химия, техника, информатика, биология, психология и др.). Таким образом, расширяется круг школьников, для которых математика становится значимым предметом.
Для жизни в современном обществе важным является формирование математического стиля мышления, проявляющегося в определенных умственных навыках. В процессе математической деятельности в арсенал приемов и методов человеческого мышления естественным образом включаются индукция и дедукция, обобщение и конкретизация, анализ и синтез, классификация и систематизация, абстрагирование и аналогия. Объекты математических умозаключений и правила их конструирования вскрывают механизм логических построений, вырабатывают умения формулировать, обосновывать и доказывать суждения, тем самым развивают логическое мышление. Ведущая роль принадлежит математике в формировании алгоритмического мышления и воспитании умений действовать по заданному алгоритму и конструировать новые. В ходе решения задач — основной учебной деятельности на уроках математики — развиваются творческая и прикладная стороны мышления.
Обучение математике дает возможность развивать у учащихся точную, экономную и информативную речь, умение отбирать наиболее подходящие языковые (в частности, символические, графические) средства.
Математическое образование вносит свой вклад в формирование общей культуры человека. Необходимым компонентом общей культуры в современном толковании является общее знакомство с методами познания действительности, представление о предмете и методе математики, его отличия от методов естественных и гуманитарных наук, об особенностях применения математики для решения научных и прикладных задач.
Изучение математики способствует эстетическому воспитанию человека, пониманию красоты и изящества математических рассуждений, восприятию геометрических форм, усвоению идеи симметрии.
История развития математического знания дает возможность пополнить запас историко-научных знаний школьников, сформировать у них представления о математике как части общечеловеческой культуры. Знакомство с основными историческими вехами возникновения и развития математической науки, с историей великих открытий, именами людей, творивших науку, должно войти в интеллектуальный багаж каждого культурного человека.
5. Результаты изучения учебного предмета
Изучение математики в основной школе дает возможность обучающимся достичь следующих результатов развития:
1) в личностном направлении:
• умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры;
• критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта;
• представление о математической науке как сфере человеческой деятельности, об этапах ее развития, о ее значимости для развития цивилизации;
• креативность мышления, инициатива, находчивость, активность при решении математических задач;
• умение контролировать процесс и результат учебной математической деятельности;
• способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений;
2) в метапредметном направлении:
• первоначальные представления об идеях и о методах математики как универсальном языке науки и техники, средстве моделирования явлений и процессов;
• умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;
• умение находить в различных источниках информацию, необходимую для решения математических проблем, представлять ее в понятной форме, принимать решение в условиях неполной и избыточной, точной и вероятностной информации;
• умение понимать и использовать математические средства наглядности (графики, диаграммы, таблицы, схемы и др.) для иллюстрации, интерпретации, аргументации;
• умение выдвигать гипотезы при решении учебных задач, понимать необходимость их проверки;
• умение применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач;
• понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом;
• умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем;
• умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера;
3) в предметном направлении:
• овладение базовым понятийным аппаратом по основным разделам содержания, представление об основных изучаемых понятиях (число, геометрическая фигура, уравнение, функция, вероятность) как важнейших математических моделях, позволяющих описывать и изучать реальные процессы и явления;
• умение работать с математическим текстом (анализировать, извлекать необходимую информацию), грамотно применять математическую терминологию и символику, использовать различные языки математики;
• умение проводить классификации, логические обоснования, доказательства математических утверждений;
• развитие представлений о числе и числовых системах от натуральных до действительных чисел, овладение навыками устных, письменных, инструментальных вычислений;
• овладение символьным языком алгебры, приемами выполнения тождественных преобразований рациональных выражений, решения уравнений, систем уравнений, неравенств и систем неравенств, умение использовать идею координат на плоскости для интерпретации уравнений, неравенств, систем, умение применять алгебраические преобразования, аппарат уравнений и неравенств для решения задач из различных разделов курса;
• овладение системой функциональных понятий, функциональным языком и символикой, умение на основе функционально-графических представлений описывать и анализировать реальные зависимости;
• овладение основными способами представления и анализа статистических данных; наличие представлений о статистических закономерностях в реальном мире и о различных способах их изучения, о вероятностных моделях;
• умение применять изученные понятия, результаты, методы для решения задач практического характера и задач из смежных дисциплин с использованием при необходимости справочных материалов, калькулятора, компьютера.
6. Основное содержание
Повторение курса алгебры 8 класса (4 ч)
Алгебраические уравнения. Системы нелинейных уравнений (15 ч)
Деление многочленов. Решение алгебраических уравнений. Уравнения, сводящиеся к алгебраическим. Системы нелинейных уравнений с двумя неизвестными. Различные способы решения систем уравнений. Решение задач с помощью систем уравнений.
Основная цель - обучить делению многочленов, решению алгебраических уравнений и систем уравнений.
Степень с рациональным показателем (8 ч)
Степень с целым показателем и ее свойства. Возведение числового неравенства в степень с натуральным показателем. (Корень -й степени , степень с рациональным показателем – изучается при 4 ч в неделю).
-й степени , степень с рациональным показателем – изучается при 4 ч в неделю).
Основная цель – сформировать понятие с целым показателем; выработать умение выполнять преобразования простейших выражений, содержащих степень с целым показателем; ввести понятия корня  -й степени и степени с рациональным показателем.
-й степени и степени с рациональным показателем.
Степенная функция (18 ч)
Область определения функции. Возрастание и убывание функции. Четность и нечетность функции. Функция 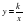 .
.
Основная цель – выработать умение исследовать по заданному графику функции 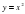 ,
, 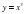 ,
, 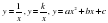 .
.
Элементы тригонометрии (8 ч)
Радианная мера угла. Поворот точки вокруг начала координат. Определение синуса,
косинуса и тангенса угла. Знаки синуса, косинуса и тангенса. Зависимость между синусом, косинусом и тангенсом одного и того же угла.
Основная цель – ввести понятия синуса, косинуса, тангенса и котангенса произвольного угла; сформировать умения вычислять по известному значению одной из тригонометрических функций значения остальных тригонометрических функций, выполнять несложные преобразования тригонометрических выражений.
Прогрессии (14 ч)
Числовая последовательность. Арифметическая и геометрическая прогрессии. Формулы n-го члена и суммы п первых членов арифметической и геометрической прогрессий.
Основная цель — познакомить учащихся с понятиями арифметической и геометрической прогрессий.
6. Случайные события (13 ч)
События невозможные, достоверные, случайные. Совместные и несовместные события. Равновозможные события. Классическое определение вероятности события. Представление о геометрической вероятности. Решение вероятностных задач с помощью комбинаторики. Противоположные события и их вероятности. Относительная частота и закон больших чисел. Тактика игр, справедливые и несправедливые игры.
Основная цель — познакомить учащихся с различными видами событий, с понятием вероятности события и с различными подходами к определению этого понятия; сформировать умения нахождения вероятности события, когда число равновозможных исходов испытания очевидно; обучить нахождению вероятности события после проведения серии однотипных испытаний.
7. Случайные величины (12 ч)
Таблицы распределения значений случайной величины. Наглядное представление распределения случайной величины: полигон частот, диаграммы круговые, линейные, столбчатые, гистограмма. Генеральная совокупность и выборка. Репрезентативная выборка. Характеристики выборки: размах, мода, медиана, среднее. Представление о законе нормального распределения.
Основная цель — сформировать представления о закономерностях в массовых случайных явлениях; выработать умение сбора и наглядного представления статистических данных; обучить нахождению центральных тенденций выборки.
8. Повторение. Решение задач по курсу алгебры 7 – 9 классов (13 ч)
График контрольных работ
| Дата | Тема |
| 15.10. | Алгебраические уравнения. Системы нелинейных уравнений |
| 31.10. | Степень с рациональным показателем |
| 19.12. | Степенная функция |
| 27.02. | Прогрессии |
| 3.04. | Случайные события |
| 8.05. | Случайные величины |
7. Тематическое планирование с определением основных видов учебной деятельности
| Содержание материала | Характеристика основных видов деятельности ученика (на уровне учебных действий) |
| Повторение курса алгебры 8 класса (4 часа) |
| Глава I. Алгебраические уравнения. Системы нелинейных уравнений (15 часов) |
| Деление многочленов Решение алгебраических уравнений Уравнения, сводящиеся к алгебраическим Системы нелинейных уравнений с двумя неизвестными Различные способы решения систем уравнений Решение задач с помощью систем уравнений Обобщающий урок | Выполнять деление многочлена на многочлен. Знать способы поиска корня алгебраического уравнения. Решать алгебраические уравнения третьей и четвертой степени, уравнения, сводящиеся к алгебраическим (в том числе возвратные). Определить, является ли пара чисел решением данного уравнения с двумя неизвестными; приводить примеры решений уравнений с двумя переменными, обозначенные в содержании. Решать задачи, алгебраической моделью которых является система нелинейных уравнений с двумя неизвестными. Решать системы двух нелинейных уравнений с двумя неизвестными. Решать текстовые задачи алгебраическим способом: переходить от словесной формулировки условия задачи к алгебраической модели путём составления системы уравнений; решать составленную систему уравнений; интерпретировать результат. |
| Глава II. Степень с рациональным показателем (8 часов) |
| Повторение свойств степени с натуральным показателем Степень с целым показателем Арифметический корень натуральной степени. Свойства арифметического корня Степень с рациональным показателем. Возведение в степень числового неравенства. | Сравнивать и упорядочивать степени с целыми и рациональными показателями; выполнять вычисления с рациональными числами, вычислять значения степеней с целым показателем. Формулировать определение арифметического корня натуральной степени из числа. Вычислять приближённые значения корней, используя при необходимости калькулятор; проводить оценку корней. Применять свойства арифметического корня для преобразования выражений. Формулировать определение корня третьей степени; находить значения кубических корней, при необходимости используя калькулятор. Исследовать свойства кубического корня, проводя числовые эксперименты с использованием калькулятора, компьютера. Возводить числовое неравенство с положительными левой и правой частью в степень. Сравнивать степени с разными основаниями и равными показателями. Формулировать определение степени с рациональным показателем, применять свойства степени с рациональным показателем при вычислениях |
| Глава III. Степенная функция (18 часов) |
| Область определения функции. Возрастание и убывание функции. Четность и нечетность функции.
Функция 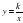 . . Неравенства и уравнения, содержащие степень | Вычислять значения функций, заданных формулами (при необходимости использовать калькулятор); Составлять таблицы значений функций. Формулировать определение функции. Строить по точкам графики функций. Описывать свойства функции на основе её графического представления (область определения, множество значений, промежутки знакопостоянства, чётность, нечётность, возрастание, убывание, наибольшее, наименьшее значения). Интерпретировать графики реальных зависимостей. Использовать функциональную символику для записи разнообразных фактов, связанных с функциями у = х , у = х, у = х , у = — , обогащая опыт выполнения знаково-символических действий. Строить речевые конструкции с использованием функциональной терминологии. Исследование графиков функций в зависимости от значений коэффициентов, входящих в формулу. Распознавать виды изучаемых функций. Строить графики указанных функций (в том числе с применением движений графиков); описывать их свойства. Решать простейшие уравнения и неравенства, содержащие степень. Решать иррациональные уравнения
|
| Глава IV. Элементы тригонометрии (8 часов) |
| Радианная мера угла Поворот точки вокруг начала координат Определение синуса, косинуса и тангенса угла Знаки синуса, косинуса и тангенса Зависимость между синусом, косинусом и тангенсом одного и того же угла Тригонометрические тождества | Знать угол в 1 радиан; единичная окружность; Выражать градусные меры углов в радианах и радианные меры в градусах; Уметь обозначать на единичной окружности точки с заданными координатами, читать единичную окружность Формулировать определения синуса, косинуса, тангенса, котангенса угла  ; ; Таблица значений тригонометрических функций углов 30о, 45о, 60о. Исследование тригонометрических функций; Формулировать основные тригонометрические тождества, формулы сложения, формулы синуса и косинуса двойного угла, формулы приведения Применять основные тригонометрические тождества, формулы сложения, формулы синуса и косинуса двойного угла, формулы приведения для нахождения значений тригонометрических выражений. Уметь доказывать тригонометрические тождества; упрощать тригонометрические выражения; вычислять значения тригонометрических выражений |
| Глава IV. Прогрессии (14 часов) |
| Числовая последовательность Арифметическая прогрессия Сумма  первых членов арифметической прогрессии первых членов арифметической прогрессии Геометрическая прогрессия Сумма  первых членов геометрической прогрессии первых членов геометрической прогрессии
| Применять индексные обозначения, строить речевые высказывания с использованием терминологии, связан-ной с понятием последовательности. Вычислять члены последовательностей, заданных формулой  -го члена или рекуррентной формулой. -го члена или рекуррентной формулой. Устанавливать закономерность в построении последовательности, если вы-писаны первые несколько её членов. Изображать члены последовательности точками на координатной плоскости. Распознавать арифметическую и геометрическую прогрессии при разных способах задания. Выводить на основе доказательных рассуждений формулы общего члена арифметической и геометрической прогрессий, суммы первых  членов арифметической и геометрической прогрессий; решать задачи с использованием этих формул. Рассматривать примеры из реальной жизни, иллюстрирующие изменение процессов в арифметической прогрессии, в геометрической прогресс-сии; изображать соответствующие зависимости графи-чески. членов арифметической и геометрической прогрессий; решать задачи с использованием этих формул. Рассматривать примеры из реальной жизни, иллюстрирующие изменение процессов в арифметической прогрессии, в геометрической прогресс-сии; изображать соответствующие зависимости графи-чески. Решать задачи на сложные проценты, в том числе задачи из реальной практики (с использованием калькулятора) |
| Глава V. Случайные события (13 часов) |
| События Вероятность события. Решение вероятностных задач с помощью комбинаторики Геометрическая вероятность Относительная частота и закон больших чисел
| Находить вероятность события в испытаниях с равновозможными исходами (с применением классического определения вероятности). Проводить случайные эксперименты, в том числе с помощью компьютерного моделирования, интерпретировать их результаты. Вычислять частоту случайного события; оценивать вероятность с помощью частоты, полученной опытным путём. Приводить примеры достоверных и невозможных событий. Объяснять значимость маловероятных событий в зависимости от их последствий. Решать задачи на нахождение вероятностей событий, в том числе с применением комбинаторики. Приводить примеры противоположных событий. Использовать при решении задач свойство вероятностей противоположных событий. |
| Глава VI. Случайные величины (12 часов) |
| Таблицы распределения Полигоны частот Генеральная совокупность и выборка Размах и центральные тенденции | Организовывать информацию и представлять её в виде таблиц, столбчатых и круговых диаграмм. Находить среднее арифметическое, размах, моду и медиану совокупности числовых данных. Приводить содержательные примеры использования средних значений для характеристики совокупности данных (спортивные показатели, размеры одежды и др.). |
| Повторение курса алгебры (13 часов) |
8. Материально – техническое обеспечение образовательного процесса
Кабинет математики является неотъемлемой частью информационно-образовательной среды по предмету. В нем проводятся внеклассные и внеурочные занятия, воспитательная работа с учащимися. Поэтому он необходим в школе, а его оснащение должно соответствовать требованиям государственного образовательного стандарта. Основа кабинета - рабочие места для учащихся и учителя.
Оборудование кабинета:
- комплект технических и информационно-коммуникативных средств обучения:
- аппаратура воспроизведения аудио- и видеоинформации,
- компьютер,
- мультимедиапроектор,
- интерактивную доску,
- медиатеку,
- электронная база данных для создания тематических и итоговых разноуровневых
трениировочных и проверочных материалов для организации фронтальной и индивидуальной
работы,
- интернет,
- комплект тематических таблиц по всем разделам школьного курса математики;
- портреты выдающихся деятелей математики;
- учебно-методической, справочно-информационной и научно-популярной литература:
1) Нормативные документы: Примерная программа основного общего образования по математике, Планируемые результаты освоения программы основного общего образования по математике.
2) Авторские программы по курсам математики.
3) Учебники: по математике для 5—6 классов, по алгебре для 7—9 классов, по геометрии для 7—9 классов.
4) Учебные пособия: рабочие тетради, дидактические материалы, сборники контрольных работ.
5) Пособия для подготовки и проведения государственной аттестации по математике за курс основной школы.
6) Учебные пособия по элективным курсам.
7) Научная, научно-популярная, историческая литература.
8) Справочные пособия (энциклопедии, словари, справочники по математике и т.п.).
9) Методические пособия для учителя.
- картотеку с заданиями для индивидуального обучения, организации самостоятельных работ обучающихся, проведения контрольных работ и т. д.;
- Учебно-практическое и учебно-лабораторное оборудование:
1) комплект чертежных инструментов : линейка, циркуль, транспортир, угольник (30°, 60°, 90°), угольник (45°, 90°).
2) Комплекты планиметрических и стереометрических тел (демонстрационных и раздаточных),
9. Линия учебно-методических комплектов авторов
III. А. Алимова и др.
1. Алимов Ш. А. Алгебра, 7 кл.: учебник для общеобразовательных учреждений / Ш. А. Алимов, Ю. М. Колягин, М. В. Ткачёва, Ю. В. Сидоров, Н. Е. Фёдорова, М. И. Шабунин. — М.: Просвещение, 2011.
2. Алимов Ш. А. Алгебра, 8 кл.: учебник для общеобразовательных учреждений / Ш. А. Алимов, Ю. М. Колягин, М. В. Ткачёва, Ю. В. Сидоров, Н. Е. Фёдорова, М. И. Шабунин. — М.: Просвещение, 2011.
3. Алимов Ш. А. Алгебра, 9 кл.: учебник для общеобразовательных учреждений / III.А. Алимов, Ю. М. Колягин, М. В. Ткачёва, Ю. В. Сидоров, Н. Е. Фёдорова, М. И. Шабунин. — М.: Просвещение, 2011.
4. Колягин Ю. М. Алгебра, 7 кл.: рабочая тетрадь, в 2 ч. / Ю. М. Колягин,М. В. Ткачёва, Н. Е. Фёдорова, М. И. Шабунин. — М.: Просвещение, 2011.
5. Калягин Ю. М. Алгебра, 8 кл.: рабочая тетрадь, в 2 ч. / Ю. М. Колягин,М. В. Ткачёва, Н. Е. Фёдорова, М. И. Шабунин. — М.: Просвещение, 2011.
6. Калягин Ю. М. Алгебра, 9 кл.: рабочая тетрадь/ Ю. М. Колягин, К).В. Сидоров и др. — М.: Просвещение 2011.
7. Колягин Ю. М. Изучение алгебры, 7 — 9 кл.: книга для учителя / М. Ю. Колягин, Ю. В. Сидоров, М. В. Ткачёва и др. — М.: Просвещение, 2011.
8. Ткачёва М. В. Алгебра, 7 кл.: дидактические материалы / М. В. Ткачёва, Н. Е. Фёдорова, М. И. Шабунин. — М.: Просвещение, 2011.
9. Ткачёва М. В. Алгебра, 7 кл.: тематические тесты. ГИА/ М. В. Ткачёва. — М.: Просвещение, 2011.
10. Ткачёва М. В. Алгебра, 8 кл.: дидактические материалы/ М. В. Ткачёва, Н. Е. Фёдорова, М. И. Шабунин. — М.: Просвещение, 2011.
И. Ткачёва М. В. Алгебра, Вкл.: тематические тесты. ГИА/ М. В. Ткачёва. — М.: Просвещение, 2011.
12. Ткачёва М. В. Алгебра, 9 кл.: дидактические материалы/ М.В.Ткачёва, Н.Е.Фёдорова, М. И. Шабунин. — М.: Просвещение, 2011.
13. Ткачёва М. В. Алгебра, 9 кл.: тематические тесты / М. В. Ткачёва. — М.: Просвещение, 2011.

 Получите свидетельство
Получите свидетельство Вход
Вход


 -й степени , степень с рациональным показателем – изучается при 4 ч в неделю).
-й степени , степень с рациональным показателем – изучается при 4 ч в неделю). 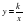 .
.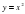 ,
, 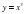 ,
, 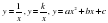 .
.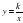 .
. ;
; 








 Рабочая программа по алгебре (9 класс) (64.57 КB)
Рабочая программа по алгебре (9 класс) (64.57 КB)
 0
0 503
503 48
48 Нравится
0
Нравится
0


