Рабочая программа по алгебре (7 класс)

1.ПОЯСНИТЕЛЬНАЯ ЗАПИСКА.

1.1 Нормативно-правовая база.

          Рабочая программа по математике составлена на основе федерального компонента государственного стандарта основного общего образования. 

          Данная рабочая программа ориентирована на учащихся 7 классов, соответствует учебнику « Алгебра» для 7 класса общеобразовательных учреждений / Ю.Н.Макарычев, Н.Г.Миндюк, К.И.Нешков, С.Б.Суворова / Просвещение, 2005-2010г.

1.2 Место предмета в федеральном базисном учебном плане.

Рабочая программа курса алгебры 7 класса рассчитана на 136 часов ( 4 часа в неделю при 34 неделях в год) .102 часа  согласно Федеральному базисному учебному плану для образовательных учреждений Российской Федерации и 34 часов из школьного и регионального компонента).

1.3 Причины создания рабочей программы.

Дополнительные 34 часа  позволяют глубже изучить наиболее трудные для учащихся темы, рассмотреть большее количество разнообразных задач и упражнений изучаемых тем. Согласно учебного плану МБОУ-СОШ №33 программа рассчитана на 136  часов в год (4 часа в неделю).

1.4 Общая характеристика учебного предмета.

Курс характеризуется повышением теоретического уровня обучения, постепенным усилением роли теоретических обобщений и дедуктивных заключений. Прикладная направленность курса обеспечивается систематическим обращением к примерам, раскрывающим возможности применения математики к изучению действительности и решению практических задач.

В ходе освоения содержания курса учащиеся получают возможность:

развить представления о числе и роли вычислений в человеческой практике; сформировать практические навыки выполнения устных, письменных, инструментальных вычислений, развить вычислительную культуру;

овладеть символическим языком алгебры, выработать формально-оперативные алгебраические умения и научиться применять их к решению математических и нематематических задач;

изучить свойства и графики элементарных функций, научиться использовать функционально-графические представления для описания и анализа реальных зависимостей;

развить пространственные представления и изобразительные умения, освоить основные факты и методы планиметрии, познакомиться с простейшими пространственными телами и их свойствами;

получить представления о статистических закономерностях в реальном мире и о различных способах их изучения, об особенностях выводов и прогнозов, носящих вероятностный характер;

развить логическое мышление и речь – умениия логически обосновывать суждения, проводить несложные систематизации, приводить примеры и контрпримеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства;

сформировать представления об изучаемых понятиях и методах как важнейших средствах математического моделирования реальных процессов и явлений.

Учебно-тематический план:

Весь материал -с мотрите документ.

Муниципальное бюджетное образовательное учреждение

средняя общеобразовательная школа № 33 имени

Героя Советского Союза Л.П. Тихмянова

УТВЕРЖДАЮ

Директор МБОУ - СОШ № 33

_____________ Н.Н. Акулова

приказ _______от ______2012 года

РАБОЧАЯ ПРОГРАММА

по алгебре

в 7 « А » классе

2012 – 2013 учебный год

Составитель программы:

учитель математики

Панина Елена Юрьевна

Программа рассмотрена на заседании школьного методического объединения

Протокол № __ от «__»_________2012г.

Руководитель__________________________( _______ __________)

1.ПОЯСНИТЕЛЬНАЯ ЗАПИСКА.

1.1 Нормативно-правовая база.

Рабочая программа по математике составлена на основе федерального компонента государственного стандарта основного общего образования. 
Данная рабочая программа ориентирована на учащихся 7 классов и реализуется на основе следующих документов: 

1.Закон РФ «Об образовании», п.7,ст.32;

2. Письмо Департамента образования от 13.11.2002 г. «»О развитии содержания

общего образования.

3.Программа для общеобразовательных школ, гимназий, лицеев: 
Сборник “Программы для общеобразовательных школ, гимназий, лицеев:

Математика. 5-11 кл.”/ Сост. Г.М.Кузнецова, Н.Г. Миндюк. – 3-е изд., стереотип.-

М. Дрофа, 2002; 4-е изд. – 2004г. 
4.Стандарт основного общего образования по математике. 
Стандарт основного общего образования по математике //Математика в школе. –

2004г,-№4, -с.4

5.Федерального перечня учебников, рекомендованных Министерством образования

Российской Федерации к использованию в образовательном процессе в

общеобразовательных учреждениях на 2012-2013 учебный год,

Данная рабочая программа ориентирована на учащихся 7классов, соответствует учебнику « Алгебра» для 7 класса общеобразовательных учреждений / Ю.Н.Макарычев, Н.Г.Миндюк, К.И.Нешков, С.Б.Суворова / Просвещение, 2005-2010г.

1.2 Место предмета в федеральном базисном учебном плане.

Рабочая программа курса алгебры 7 класса рассчитана на 136 часов ( 4 часа в неделю при 34 неделях в год) .102 часа согласно Федеральному базисному учебному плану для образовательных учреждений Российской Федерации и 34 часов из школьного и регионального компонента).

1.3 Причины создания рабочей программы.

Дополнительные 34 часа позволяют глубже изучить наиболее трудные для учащихся темы, рассмотреть большее количество разнообразных задач и упражнений изучаемых тем. Согласно учебного плану МБОУ-СОШ №33 программа рассчитана на 136 часов в год (4 часа в неделю).

1.4 Общая характеристика учебного предмета.

Курс характеризуется повышением теоретического уровня обучения, постепенным усилением роли теоретических обобщений и дедуктивных заключений. Прикладная направленность курса обеспечивается систематическим обращением к примерам, раскрывающим возможности применения математики к изучению действительности и решению практических задач.

В ходе освоения содержания курса учащиеся получают возможность:

• развить представления о числе и роли вычислений в человеческой практике; сформировать практические навыки выполнения устных, письменных, инструментальных вычислений, развить вычислительную культуру;

• овладеть символическим языком алгебры, выработать формально-оперативные алгебраические умения и научиться применять их к решению математических и нематематических задач;

• изучить свойства и графики элементарных функций, научиться использовать функционально-графические представления для описания и анализа реальных зависимостей;

• развить пространственные представления и изобразительные умения, освоить основные факты и методы планиметрии, познакомиться с простейшими пространственными телами и их свойствами;

• получить представления о статистических закономерностях в реальном мире и о различных способах их изучения, об особенностях выводов и прогнозов, носящих вероятностный характер;

• развить логическое мышление и речь – умениия логически обосновывать суждения, проводить несложные систематизации, приводить примеры и контрпримеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства;

• сформировать представления об изучаемых понятиях и методах как важнейших средствах математического моделирования реальных процессов и явлений.

1.5 Цели обучения.

1) в направлении личностного развития
• развитие логического и критического мышления, культуры речи, способности к умственному эксперименту;
• формирование у учащихся интеллектуальной честности и объективности, способности к преодолению мыслительных стереотипов, вытекающих из обыденного опыта;
• воспитание качеств личности, обеспечивающих социальную мобильность, способность принимать самостоятельные решения;
• формирование качеств мышления, необходимых для адаптации в современном информационном обществе;
• развитие интереса к математическому творчеству и математических способностей;

2) в метапредметном направлении
• формирование представлений о математике как части общечеловеческой культуры, о значимости математики в развитии цивилизации и современного общества;
• развитие представлений о математике как форме описания и методе познания действительности, создание условий для приобретения первоначального опыта математического моделирования;
• формирование общих способов интеллектуальной деятельности, характерных для математики и являющихся основой познавательной культуры, значимой для различных сфер человеческой деятельности;

3) в предметном направлении
• овладение математическими знаниями и умениями, необходимыми для продолжения обучения в старшей школе или иных общеобразовательных учреждениях, изучения смежных дисциплин, применения в повседневной жизни;
• создание фундамента для математического развития, формирования механизмов мышления, характерных для математической деятельности.

1.6 Структура рабочей программы.

Рабочая программа включает следующие разделы:

пояснительную запи­ску;

• основное содержание;

• примерное распределение учебных часов по разделам программы;

• требования к уровню подготовки учащихся данного класса;

• тематическое планирование учебного материала;

• поурочное планирование;

• примерные контрольные работы;

• учебное и учебно-методическое обеспечение обучения.

1.7 Обоснование увеличения/ уменьшения часов.

В настоящей рабочей программе изменено соотношение часов на изучение тем, в связи с их сложностью. Для более широкого знакомства с математикой введен курс «Элементы статистики и теории вероятностей» в количестве 4 часов. На этом этапе продолжается решение задач путем перебора возможных вариантов, изучается статистический подход к понятию вероятности. Дается классическое определение вероятности, формируются умения вычислять вероятности с помощью формул комбинаторики. Особое внимание уделяется правилу сложения вероятностей.

1.8 Формы и методы обучения.

Основной формой организации учебного процесса является классно-урочная система. В качестве дополнительных форм организации образовательного процесса по данной программе используется система консультационной поддержки, индивидуальных занятий, работа учащихся с использованием современных информационных технологий: игровое моделирование (дидактические игры, работа в малых группах, работа в парах сменного состава); проблемное обучение; личностно ориентированное обучение.

Теоретический материал курса излагается на наглядно-интуитивном уровне, математические методы и законы формулируются в виде правил. Курс строится на индуктивной основе с привлечением дедуктивных рассуждений.

Учебный процесс ориентирован на:

• создание оптимальных условий обучения;

• исключение психотравмирующих факторов;

•    сохранение психосоматического состояния здоровья учащихся;

•    развитие положительной мотивации к освоению программы;

•  развитие индивидуальности и одаренности каждого ребенка.
  
  

• рациональное сочетание устных и письменных видов работы как при изучении теории, так и при решении задач;

• сбалансированное сочетание традиционных и новых методов обучения;

• оптимизированное применение объяснительно-иллюстративных и эвристических методов;

• использование современных технических средств обучения.

2.ТРЕБОВАНИЯ К УРОВНЮ ПОДГОТОВКИ УЧАЩИХСЯ.

знать/понимать

• существо понятия математического доказательства; примеры доказательств;

• существо понятия алгоритма; примеры алгоритмов;

• как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;

• как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;

• как потребности практики привели математическую науку к необходимости расширения понятия числа;

• вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов;

• каким образом геометрия возникла из практических задач землемерия; примеры геометрических объектов и утверждений о них, важных для практики;

• смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации;

уметь

• составлять буквенные выражения и формулы по условиям задач, осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;

• выполнять основные действия со степенями с натуральным показателем, с многочленами; выполнять тождественные преобразования целых выражений; выполнять разложение многочленов на множители;

• решать линейные уравнения и уравнения, сводящиеся к ним, системы двух линейных уравнений,

• решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;

• изображать числа точками на координатной прямой

• определять координаты точки плоскости, строить точки с заданными координатами;

• находить значение функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;

• описывать свойства изученных функций (y = kx + b, y = kx, y = x2, y = x3) и строить их графики.

использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

• выполнения расчётов по формулам, составления формул, выражающих зависимость между реальными величинами; нахождения нужной формулы в справочных материалах;

• моделирования практических ситуаций и исследование построенных моделей с использованием аппарата алгебры; описания зависимости между физическими величинами соответствующими формулами при исследовании несложных практических ситуаций;

• интерпретации графиков реальных зависимостей между величинами.

3.УЧЕБНО - ТЕМАТИЧЕСКИЙ ПЛАН.

4. СОДЕРЖАНИЕ ПРОГРАММЫ УЧЕБНОГО КУРСА.

Содержание тем учебного курса

Количество часов 136 ч.

Алгебра 7 класс

Повторение курса математики 6 класса (4 часа).

ГЛАВА 1. Выражения, тождества, уравнения. Статистические характеристики. (26 часов)

Числовые выражения с переменными. Простейшие преобразования выражений. Уравнение, корень уравнения. Линейное уравнение с одной переменной. Решение текстовых задач методом составления уравнений.

Цель: систематизировать и обобщить сведения о преобразованиях алгебраических выражений и решении уравнений с одной переменной.

Первая тема курса 7 класса является связующим звеном между курсом математики 5—6 классов и курсом алгебры. В ней закрепляются вычислительные навыки, систематизируются и обобщаются сведения о преобразованиях выражений и решении уравнений.

Нахождение значений числовых и буквенных выражений даёт возможность повторить с обучающимися правила действий с рациональными числами. Умения выполнять арифметические действия с рациональными числами являются опорными для всего курса алгебры. Следует выяснить, насколько прочно овладели ими учащиеся, и в случае необходимости организовать повторение с целью ликвидации выявленных пробелов. Развитию навыков вычислений должно уделяться серьезное внимание и в дальнейшем при изучении других тем курса алгебры.

В связи с рассмотрением вопроса о сравнении значений выражений расширяются сведения о неравенствах: вводятся знаки ≥ и ≤, дается понятие о двойных неравенствах.

При рассмотрении преобразований выражений формально-оперативные умения остаются на том же уровне, учащиеся поднимаются на новую ступень в овладении теорией. Вводятся понятия «тождественно равные выражения», «тождество», «тождественное преобразование выражений», содержание которых будет постоянно раскрываться и углубляться при изучении преобразований различных алгебраических выражений. Подчеркивается, что основу тождественных преобразований составляют свойства действий над числами.

Усиливается роль теоретических сведений при рассмотрении уравнений. С целью обеспечения осознанного восприятия обучающимися алгоритмов решения уравнений вводится вспомогательное понятие равносильности уравнений, формулируются и разъясняются на конкретных примерах свойства равносильности. Дается понятие линейного уравнения и исследуется вопрос о числе его корней. В системе упражнений особое внимание уделяется решению уравнений вида ах=b при различных значениях а и b. Продолжается работа по формированию у обучающихся умения использовать аппарат уравнений как средство для решения текстовых задач. Уровень сложности задач здесь остается таким же, как в 6 классе.

Ознакомление обучающихся с простейшими статистическими характеристиками: средним арифметическим, модой, медианой, размахом. Учащиеся должны уметь пользовать эти характеристики для анализа ряда данных в несложных ситуациях.

Глава 2. Функции (18 часов)

Функция, область определения функции. Вычисление значений функции по формуле. График функции. Прямая пропорциональность и ее график. Линейная функция и её график.

Цель: ознакомить обучающихся с важнейшими функциональными понятиями и с графиками прямой пропорциональности и линейной функции общего вида.

Данная тема является начальным этапом в систематической функциональной подготовке обучающихся. Здесь вводятся такие понятия, как функция, аргумент, область определения функции, график функции. Функция трактуется как зависимость одной переменной от другой. Учащиеся получают первое представление о способах задания функции. В данной теме начинается работа по формированию у обучающихся умений находить по формуле значение функции по известному значению аргумента, выполнять ту же задачу по графику и решать по графику обратную задачу. Функциональные понятия получают свою конкретизацию при изучении линейной функции и ее частного вида — прямой пропорциональности. Умения строить и читать графики этих функций широко используются как в самом курсе алгебры, так и в курсах геометрии и физики. Учащиеся должны понимать, как влияет знак коэффициента на расположение в координатной плоскости графика функции у=кх, где к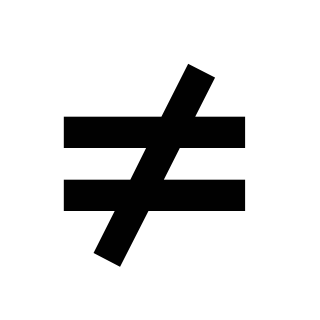0, как зависит от значений к и b взаимное расположение графиков двух функций вида у=кх+b.

Формирование всех функциональных понятий и выработка соответствующих навыков, а также изучение конкретных функций сопровождаются рассмотрением примеров реальных зависимостей между величинами, что способствует усилению прикладной направленности курса алгебры.

Глава 3. Степень с натуральным показателем ( 19 часов )

Степень с натуральным показателем и ее свойства. Одночлен. Функции у=х², у=х³ и их графики.

Цель: выработать умение выполнять действия над степенями с натуральными показателями.

В данной теме дается определение степени с натуральным показателем. В курсе математики 6 класса учащиеся уже встречались с примерами возведения чисел в степень. В связи с вычислением значений степени в 7 классе дается представление о нахождении значений степени с помощью калькулятора; Рассматриваются свойства степени с натуральным показателем: На примере доказательства свойств а^m · аⁿ = а^m+n; а^m : аⁿ = а^m-n, где m n; (а^m)ⁿ = а^m·n; (ab)^m = a^mb^m учащиеся впервые знакомятся с доказательствами, проводимыми на алгебраическом материале. Указанные свойства степени с натуральным показателем находят применение при умножении одночленов и возведении одночленов в степень. При нахождении значений выражений содержащих степени, особое внимание следует обратить на порядок действий.

Рассмотрение функций у=х², у=х³ позволяет продолжить работу по формированию умений строить и читать графики функций. Важно обратить внимание обучающихся на особенности графика функции у=х²: график проходит через начало координат, ось Оу является его осью симметрии, график расположен в верхней полуплоскости.

Умение строить графики функций у=х² и у=х³ используется для ознакомления обучающихся с графическим способом решения уравнений.

Глава 4. Многочлены ( 23 часа )

Многочлен. Сложение, вычитание и умножение многочленов. Разложение многочленов на множители.

Цель: выработать умение выполнять сложе­ние, вычитание, умножение многочленов и разложение многочленов на множители.

Данная тема играет фундаментальную роль в формировании умения выполнять тождественные преобразования алгебраических выражений. Формируемые здесь формально-оперативные умения являются опорными при изучении действий с рациональными дробями, корнями, степенями с рациональными показателями.

Изучение темы начинается с введения понятий многочлена, стандартного вида многочлена, степени многочлена. Основное место в этой теме занимают алгоритмы действий с многочленами — сложение, вычитание и умножение. Учащиеся должны понимать, что сумму, разность, произведение многочленов всегда можно представить в виде многочлена. Действия сложения, вычитания и умножения многочленов выступают как составной компонент в заданиях на преобразования целых выражений. Поэтому нецелесообразно переходить к комбинированным заданиям прежде, чем усвоены основные алгоритмы.

Серьезное внимание в этой теме уделяется разложению многочленов на множители с помощью вынесения за скобки общего множителя и с помощью группировки. Соответствующие преобразования находят широкое применение как в курсе 7 класса, так и в последующих курсах, особенно в действиях с рациональными дробями.

В данной теме учащиеся встречаются с примерами использования рассматриваемых преобразований при решении разнообразных задач, в частности при решении уравнений. Это позволяет в ходе изучения темы продолжить работу по формированию умения решать уравнения, а также решать задачи методом составления уравнений. В число упражнений включаются несложные задания на доказательство тождества.

Глава 5. Формулы сокращенного умножения ( 23 часа )

Формулы (а - b )(а + b ) = а² - b ², (а ± b)² = а²± 2а b + b², (а ± b)³ = а³ ± За² b + За b² ± b³, (а ± b) (а² 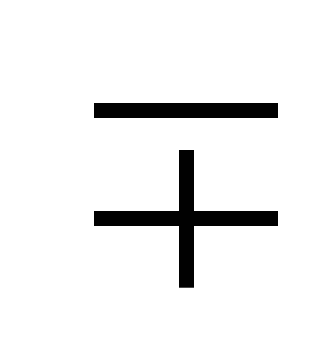а b + b²) = а³ ± b³. Применение формул сокращённого умножения в преобразованиях выражений.

Цель: выработать умение применять формулы сокращенного умножения в преобразованиях целых выражений в многочлены и в разложении многочленов на множители.

В данной теме продолжается работа по формированию у обучающихся умения выполнять тождественные преобразования целых выражений. Основное внимание в теме уделяется формулам (а - b)(а + b) = а² - b ², (а ± b)² = а²± 2а b + b². Учащиеся должны знать эти формулы и соответствующие словесные формулировки, уметь применять их как «слева направо», так и «справа налево». Наряду с указанными рассматриваются также формулы (а ± b)³ = а³ ± За² b + За b² ± b³, (а ± b) (а² 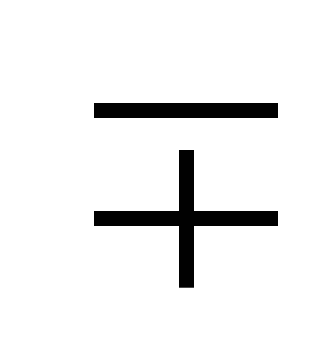а b + b²) = а³ ± b³. Однако они находят меньшее применение в курсе, поэтому не следует излишне увлекаться выполнением упражнений на их использование.

В заключительной части темы рассматривается применение различных приемов разложения многочленов на множители, а также использование преобразований целых выражений для решения широкого круга задач.

Глава 6. Системы линейных уравнений ( 19 часов )

Система уравнений. Решение системы двух линейных уравнений с двумя переменными и его геометрическая интерпретация. Решение текстовых задач методом составления систем уравнений.

Цель: ознакомить обучающихся со способом решения систем линейных уравнений с двумя переменными, выработать умение решать системы уравнений и применять их при решении текстовых задач.

Изучение систем уравнений распределяется между курсами 7 и 9 классов. В 7 классе вводится понятие системы и рассматриваются системы линейных уравнений.

Изложение начинается с введения понятия «линейное уравнение с двумя переменными». В систему упражнений включаются несложные задания на решение линейных уравнений с двумя переменными в целых числах.

Формируется умение строить график уравнения ах + bу=с, где а≠0 или b≠0, при различных значениях а, b, с. Введение графических образов даёт возможность наглядно исследовать вопрос о числе решений системы двух линейных уравнений с двумя переменными. Основное место в данной теме занимает изучение алгоритмов решения систем двух линейных уравнений с двумя переменными способом подстановки и способом сложения. Введение систем позволяет значительно расширить круг текстовых задач, решаемых с помощью аппарата алгебры. Применение систем упрощает процесс перевода данных задачи с обычного языка на язык уравнений.

Повторение ( 4 часа)

Цель: Повторение, обобщение и систематизация знаний, умений и навыков за курс алгебры 7 класса.

КАЛЕНДАРНО ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ

Класс: 7 «Б»

Годовое количество часов: 136

Количество часов в неделю: 4

Плановое количество контрольных работ: 10

I ч - 2

II ч - 1

III ч - 3

IV ч – 4

6. СРЕДСТВА КОНТРОЛЯ

В ходе реализации данной программы предусмотрены следующие виды и формы контроля: самостоятельные работы, тестирование, математические диктанты, контрольные работы. Формы учёта достижений это: проверка тетрадей по предмету, анализ текущей успеваемости, внеурочная деятельность- участие в олимпиадах, математических конкурсах.

7. УЧЕБНО – МЕТОДИЧЕСКИЕ СРЕДСТВА ОБУЧЕНИЯ .

1.Алгебра, учебник для 7 класса общеобразовательных учреждений /Ю.Н.Макарычев, Н.Г.Миндюк, К.И.Нешков, С.Б.Суворова – М.: Просвещение, 2009 г.

2.Дидактические материалы по алгебре для 7 класса/ Ю.Н.Макарычев, Н.Г.Миндюк, Л.М.Короткова/ М.: Просвещение, 2007 г.

Уроки алгебры в 7 классе /В.И.Жохов, Л.Б.Крайнева. Пособие для учителей/ М.: Просвещение, 2009 г.

3.Разноуровневые дидактические материалы по алгебре, 7 класс/ Н.Г.Миндюк, М.Б.Миндюк/ М.: Генжер, 2007 г.

4.Тесты по алгебре, 7 класс, П.И.Алтынов, М. «Экзамен», 2008 г.

5.Контрольные и проверочные работы по алгебре в 7 классе / Л.И.Звавич, Л.Я.Шляпочник, Б.В.Козулин/ Москва «Дрофа», 2005 г.