1. Пояснительная записка
Нормативные документы, в соответствии с которыми разработана рабочая программа:
Федеральный закон от 29.12.2012г. №273-ФЗ «Об образовании в Российской Федерации».
Основная образовательная программа филиала МБОУ СОШ села Каменка Самойловского района Саратовской области в селе Криуша на 2016-2017 учебный год
Федеральный государственный образовательный стандарт основного общего образования (утвержден приказом Минобрнауки России от 17.12.2010 г. № 1897, зарегистрирован в Минюсте России 01.02.2011 г., регистрационный номер 19644);
Приказ Министерства образования и науки Российской Федерации от 31 марта 2014 г. № 253 "Об утверждении федерального перечня учебников, рекомендуемых к использованию при реализации имеющих государственную аккредитацию образовательных программ основного общего образования" (с изменениями от 21 апреля 2016 года № 459).
Примерные программы основного общего образования. Математика. – (Стандарты второго поколения). – 3-е изд., перераб. – М.: Просвещение, 2012.
Алгебра. Рабочие программы. Предметная линия учебников Ю. Н. Макарычева и других. 7-9 классы: пособие для учителей общеобразоват. организаций / Н. Г. Миндюк. – 2-е изд., дораб. – М. : Просвещение, 2014. – 32с.
Учебный план филиала МБОУ СОШ села Каменка Самойловского района Саратовской области в селе Криуша на 2016-2017 учебный год
Цели и задачи:
овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, пространственных представлений, способность к преодолению трудностей;
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса;
приобретение конкретных знаний о пространстве и практически значимых умений, формирование языка описания объектов окружающего мира, для развития пространственного воображения и интуиции, математической культуры, для эстетического воспитания обучающихся. Изучение геометрии вносит вклад в развитие логического мышления, в формирование понятия доказательства.
Общая характеристика учебного предмета
Математическое образование в основной школе складывается из следующих содержательных компонентов (точные названия блоков): арифметика; алгебра; геометрия; элементы комбинаторики, теории вероятностей, статистики и логики. В своей совокупности они отражают богатый опыт обучения математике в нашей стране, учитывают современные тенденции отечественной и зарубежной школы и позволяют реализовать поставленные перед школьным образованием цели на информационно емком и практически значимом материале. Эти содержательные компоненты, развиваясь на протяжении всех лет обучения, естественным образом переплетаются и взаимодействуют в учебных курсах.
Арифметика призвана способствовать приобретению практических навыков, необходимых для повседневной жизни. Она служит базой для всего дальнейшего изучения математики, способствует логическому развитию и формированию умения пользоваться алгоритмами.
Алгебра Изучение алгебры нацелено на формирование математического аппарата для решения задач из математики, смежных предметов, окружающей реальности. Язык алгебры подчеркивает значение математики как языка для построения математических моделей, процессов и явлений реального мира (одной из основных задач изучения алгебры является развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики; овладение навыками дедуктивных рассуждений. Преобразование символических форм вносит свой специфический вклад в развитие воображения, способностей к математическому творчеству. Другой важной задачей изучения алгебры является получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов (равномерных, равноускоренных, экспоненциальных, периодических и др.), для формирования у обучающихся представлений о роли математики в развитии цивилизации и культуры.
Геометрия — один из важнейших компонентов математического образования, необходимый для приобретения конкретных знаний о пространстве и практически значимых умений, формирования языка описания объектов окружающего мира, для развития пространственного воображения и интуиции, математической культуры, для эстетического воспитания обучающихся. Изучение геометрии вносит вклад в развитие логического мышления, в формирование понятия доказательства.
Элементы логики, комбинаторики, статистики и теории вероятностей становятся обязательным компонентом школьного образования, усиливающим его прикладное и практическое значение. Этот материал необходим, прежде всего, для формирования функциональной грамотности – умений воспринимать и анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей, производить простейшие вероятностные расчёты. Изучение основ комбинаторики позволит учащемуся осуществлять рассмотрение случаев, перебор и подсчёт числа вариантов, в том числе в простейших прикладных задачах.
При изучении статистики и теории вероятностей обогащаются представления о современной картине мира и методах его исследования, формируется понимание роли статистики как источника социально значимой информации и закладываются основы вероятностного мышления.
Таким образом, в ходе освоения содержания курса учащиеся получают возможность:
развить представление о числе и роли вычислений в человеческой практике; сформировать практические навыки выполнения устных, письменных, инструментальных вычислений, развить вычислительную культуру;
овладеть символическим языком алгебры, выработать формально-оперативные алгебраические умения и научиться применять их к решению математических и нематематических задач;
изучить свойства и графики элементарных функций, научиться использовать функционально-графические представления для описания и анализа реальных зависимостей;
развить пространственные представления и изобразительные умения, освоить основные факты и методы планиметрии, познакомиться с простейшими пространственными телами и их свойствами;
получить представления о статистических закономерностях в реальном мире и о различных способах их изучения, об особенностях выводов и прогнозов, носящих вероятностный характер;
развить логическое мышление и речь – умения логически обосновывать суждения, проводить несложные систематизации, приводить примеры и контрпримеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства;
сформировать представления об изучаемых понятиях и методах как важнейших средствах математического моделирования реальных процессов и явлений.
В курсе геометрии 7 класса систематизируются знания обучающихся о простейших геометрических фигурах и их свойствах; вводится понятие равенства фигур; вводится понятие теоремы; вырабатывается умение доказывать равенство треугольников с помощью изученных признаков; вводится новый класс задач - на построение с помощью циркуля и линейки; вводится одно из важнейших понятий - понятие параллельных прямых; даётся первое представление об аксиомах и аксиоматическом методе в геометрии; вводится аксиома параллельных прямых; рассматриваются новые интересные и важные свойства треугольников (в данной теме доказывается одна из важнейших теорем геометрии — теорема о сумме углов треугольника. Она позволяет дать классификацию треугольников по углам (остроугольный, прямоугольный, тупоугольный), а также установить некоторые свойства и признаки равенства прямоугольных треугольников).
Согласно федеральному базисному учебному плану для образовательных учреждений Российской Федерации на изучение математики в 7 классе отводится 5 часов в неделю и ещё 1 час добавлен из вариативной части учебного плана для отработки устойчивых практических навыков действия с переменными, одночленами и многочленами, осознанного усвоения алгоритмов и приемов преобразования выражений, решения задач и уравнений .
Описание места учебного предмета в учебном плане
Описание места учебного предмета, курса в учебном плане
Согласно федеральному базисному учебному плану для общеобразовательнх учреждений Российской Федерации на изучение математики на ступени основного общего образования отводится не менее 875 часов из расчета 5 часов в неделю с 5 по 9 класс.
Рабочая программа для 7 класса рассчитана на 3 часа в неделю по алгебре и 2 часа в неделю по геометрии, общий объем 170 часов.
Основные формы, технологии, методы обучения, типы уроков
| Формы организации учебного процесса:
| Повторение на уроках проводится в следующих видах и формах:
|
|
|
Особое внимание уделяется повторению при проведении самостоятельных и контрольных работ.
Основной формой организации учебного процесса является классно-урочная система. В качестве дополнительных форм организации образовательного процесса по данной программе используется система консультационной поддержки, индивидуальных занятий, работа учащихся с использованием современных информационных технологий. Организация сопровождения учащихся направлена на:
создание оптимальных условий обучения;
исключение психотравмирующих факторов;
сохранение психосоматического состояния здоровья учащихся;
развитие положительной мотивации к освоению программы;
развитие индивидуальности и одаренности каждого ребенка.
Виды и формы контроля:
| Виды и формы контроля |
|
| Оценивание достижений обучающихся происходит при помощи |
|
2. Содержание программы
Глава 1. Выражения, тождества, уравнения (21 час)
Числовые выражения с переменными. Простейшие преобразования выражений. Уравнение, корень уравнения. Линейное уравнение с одной переменной. Решение текстовых задач методом составления уравнений. Статистические характеристики.
Основная цель систематизировать и обобщить сведения о преобразованиях алгебраических выражений и решении уравнений с одной переменной.
Первая тема курса 7 класса является связующим звеном между курсом математики 5—6 классов и курсом алгебры. В ней закрепляются вычислительные навыки, систематизируются и обобщаются сведения о преобразованиях выражений и решении уравнений.
Нахождение значений числовых и буквенных выражений даёт возможность повторить с обучающимися правила действий с рациональными числами. Умения выполнять арифметические действия с рациональными числами являются опорными для всего курса алгебры. Следует выяснить, насколько прочно овладели ими учащиеся, и в случае необходимости организовать повторение с целью ликвидации выявленных пробелов. Развитию навыков вычислений должно уделяться серьезное внимание и в дальнейшем при изучении других тем курса алгебры.
В связи с рассмотрением вопроса о сравнении значений выражений расширяются сведения о неравенствах: вводятся знаки ≥ и ≤, дается понятие о двойных неравенствах.
При рассмотрении преобразований выражений формально-оперативные умения остаются на том же уровне, учащиеся поднимаются на новую ступень в овладении теорией. Вводятся понятия «тождественно равные выражения», «тождество», «тождественное преобразование выражений», содержание которых будет постоянно раскрываться и углубляться при изучении преобразований различных алгебраических выражений. Подчеркивается, что основу тождественных преобразований составляют свойства действий над числами.
Усиливается роль теоретических сведений при рассмотрении уравнений. С целью обеспечения осознанного восприятия обучающимися алгоритмов решения уравнений вводится вспомогательное понятие равносильности уравнений, формулируются и разъясняются на конкретных примерах свойства равносильности. Дается понятие линейного уравнения и исследуется вопрос о числе его корней. В системе упражнений особое внимание уделяется решению уравнений вида ах=b при различных значениях а и b. Продолжается работа по формированию у обучающихся умения использовать аппарат уравнений как средство для решения текстовых задач. Уровень сложности задач здесь остается таким же, как в 6 классе.
Изучение темы завершается ознакомлением обучающихся с простейшими статистическими характеристиками: средним арифметическим, модой, медианой, размахом. Учащиеся должны уметь пользовать эти характеристики для анализа ряда данных в несложных ситуациях.
Глава 2. Функции (18 часов)
Функция, область определения функции. Вычисление значений функции по формуле. График функции. Прямая пропорциональность и ее график. Линейная функция и её график.
Основная цель ознакомить обучающихся с важнейшими функциональными понятиями и с графиками прямой пропорциональности и линейной функции общего вида.
Данная тема является начальным этапом в систематической функциональной подготовке обучающихся. Здесь вводятся такие понятия, как функция, аргумент, область определения функции, график функции. Функция трактуется как зависимость одной переменной от другой. Учащиеся получают первое представление о способах задания функции. В данной теме начинается работа по формированию у обучающихся умений находить по формуле значение функции по известному значению аргумента, выполнять ту же задачу по графику и решать по графику обратную задачу. Функциональные понятия получают свою конкретизацию при изучении линейной функции и ее частного вида — прямой пропорциональности. Умения строить и читать графики этих функций широко используются как в самом курсе алгебры, так и в курсах геометрии и физики. Учащиеся должны понимать, как влияет знак коэффициента на расположение в координатной плоскости графика функции у=кх, где к![]() 0, как зависит от значений к и b взаимное расположение графиков двух функций вида у=кх+b.
0, как зависит от значений к и b взаимное расположение графиков двух функций вида у=кх+b.
Формирование всех функциональных понятий и выработка соответствующих навыков, а также изучение конкретных функций сопровождаются рассмотрением примеров реальных зависимостей между величинами, что способствует усилению прикладной направленности курса алгебры.
Глава 3. Степень с натуральным показателем (18 часов)
Степень с натуральным показателем и ее свойства. Одночлен. Функции у=х2, у=х3 и их графики.
Основная цель: выработать умение выполнять действия над степенями с натуральными показателями.
В данной теме дается определение степени с натуральным показателем. В курсе математики 6 класса учащиеся уже встречались с примерами возведения чисел в степень. В связи с вычислением значений степени в 7 классе дается представление о нахождении значений степени с помощью калькулятора; Рассматриваются свойства степени с натуральным показателем: На примере доказательства свойств аm · аn = аm+n; аm : аn = аm-n, где m n; (аm)n = аm·n; (ab)m = ambm учащиеся впервые знакомятся с доказательствами, проводимыми на алгебраическом материале. Указанные свойства степени с натуральным показателем находят применение при умножении одночленов и возведении одночленов в степень. При нахождении значений выражений содержащих степени, особое внимание следует обратить на порядок действий.
Рассмотрение функций у=х2, у=х3 позволяет продолжить работу по формированию умений строить и читать графики функций. Важно обратить внимание обучающихся на особенности графика функции у=х2: график проходит через начало координат, ось Оу является его осью симметрии, график расположен в верхней полуплоскости.
Умение строить графики функций у=х2 и у=х3 используется для ознакомления обучающихся с графическим способом решения уравнений.
Глава 4. Многочлены (20 часов)
Многочлен. Сложение, вычитание и умножение многочленов. Разложение многочленов на множители.
Основная цель выработать умение выполнять сложение, вычитание, умножение многочленов и разложение многочленов на множители.
Данная тема играет фундаментальную роль в формировании умения выполнять тождественные преобразования алгебраических выражений. Формируемые здесь формально-оперативные умения являются опорными при изучении действий с рациональными дробями, корнями, степенями с рациональными показателями.
Изучение темы начинается с введения понятий многочлена, стандартного вида многочлена, степени многочлена. Основное место в этой теме занимают алгоритмы действий с многочленами — сложение, вычитание и умножение. Учащиеся должны понимать, что сумму, разность, произведение многочленов всегда можно представить в виде многочлена. Действия сложения, вычитания и умножения многочленов выступают как составной компонент в заданиях на преобразования целых выражений. Поэтому нецелесообразно переходить к комбинированным заданиям прежде, чем усвоены основные алгоритмы.
Серьезное внимание в этой теме уделяется разложению многочленов на множители с помощью вынесения за скобки общего множителя и с помощью группировки. Соответствующие преобразования находят широкое применение как в курсе 7 класса, так и в последующих курсах, особенно в действиях с рациональными дробями.
В данной теме учащиеся встречаются с примерами использования рассматриваемых преобразований при решении разнообразных задач, в частности при решении уравнений. Это позволяет в ходе изучения темы продолжить работу по формированию умения решать уравнения, а также решать задачи методом составления уравнений. В число упражнений включаются несложные задания на доказательство тождества.
Глава 5. Формулы сокращенного умножения (23 часа)
Формулы (а - b )(а + b ) = а2 - b 2, (а ± b)2 = а2± 2а b + b2, (а ± b)3 = а3 ± За2 b + За b2 ± b3, (а ± b) (а2 ![]() а b + b2) = а3 ± b3. Применение формул сокращённого умножения в преобразованиях выражений.
а b + b2) = а3 ± b3. Применение формул сокращённого умножения в преобразованиях выражений.
Основная цель выработать умение применять формулы сокращенного умножения в преобразованиях целых выражений в многочлены и в разложении многочленов на множители.
В данной теме продолжается работа по формированию у обучающихся умения выполнять тождественные преобразования целых выражений. Основное внимание в теме уделяется формулам (а - b)(а + b) = а2 - b 2, (а ± b)2 = а2± 2а b + b2. Учащиеся должны знать эти формулы и соответствующие словесные формулировки, уметь применять их как «слева направо», так и «справа налево». Наряду с указанными рассматриваются также формулы (а ± b)3 = а3 ± За2 b + За b2 ± b3, (а ± b) (а2 ![]() а b + b2) = а3 ± b3. Однако они находят меньшее применение в курсе, поэтому не следует излишне увлекаться выполнением упражнений на их использование.
а b + b2) = а3 ± b3. Однако они находят меньшее применение в курсе, поэтому не следует излишне увлекаться выполнением упражнений на их использование.
В заключительной части темы рассматривается применение различных приемов разложения многочленов на множители, а также использование преобразований целых выражений для решения широкого круга задач.
Глава 6. Системы линейных уравнений (14 часов)
Система уравнений. Решение системы двух линейных уравнений с двумя переменными и его геометрическая интерпретация. Решение текстовых задач методом составления систем уравнений.
Основная цель ознакомить обучающихся со способом решения систем линейных уравнений с двумя переменными, выработать умение решать системы уравнений и применять их при решении текстовых задач.
Изучение систем уравнений распределяется между курсами 7 и 9 классов. В 7 классе вводится понятие системы и рассматриваются системы линейных уравнений.
Изложение начинается с введения понятия «линейное уравнение с двумя переменными». В систему упражнений включаются несложные задания на решение линейных уравнений с двумя переменными в целых числах.
Формируется умение строить график уравнения ах + bу=с, где а≠0 или b≠0, при различных значениях а, b, с. Введение графических образов даёт возможность наглядно исследовать вопрос о числе решений системы двух линейных уравнений с двумя переменными. Основное место в данной теме занимает изучение алгоритмов решения систем двух линейных уравнений с двумя переменными способом подстановки и способом сложения. Введение систем позволяет значительно расширить круг текстовых задач, решаемых с помощью аппарата алгебры. Применение систем упрощает процесс перевода данных задачи с обычного языка на язык уравнений.
7. Повторение (6 часов)
3. Планируемые предметные результаты
Программа позволяет добиваться следующих результатов освоения образовательной программы основного общего образования:
личностные:
ответственного отношения к учению, готовности и способности обучающихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию;
формирования коммуникативной компетентности в общении и сотрудничестве со сверстниками, старшими и младшими в образовательной, учебно-исследовательской, творческой и других видах деятельности;
умения ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры;
первоначального представления о математической науке как сфере человеческой деятельности, об этапах её развития, о её значимости для развития цивилизации;
критичности мышления, умения распознавать логически некорректные высказывания, отличать гипотезу от факта;
креативности мышления, инициативы, находчивости, активности при решении арифметических задач;
умения контролировать процесс и результат учебной математической деятельности;
формирования способности к эмоциональному восприятию математических объектов, задач, решений, рассуждений;
метапредметные:
способности самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач;
умения осуществлять контроль по образцу и вносить необходимые коррективы;
способности адекватно оценивать правильность или ошибочность выполнения учебной задачи, её объективную трудность и собственные возможности её решения;
умения устанавливать причинно-следственные связи; строить логические рассуждения, умозаключения (индуктивные, дедуктивные и по аналогии) и выводы;
умения создавать, применять и преобразовывать знаковосимволические средства, модели и схемы для решения учебных и познавательных задач;
развития способности организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками: определять цели, распределять функции и роли участников, взаимодействовать и находить общие способы работы; умения работать в группе: находить общее решение и разрешать конфликты на основе согласования позиций и учёта интересов; слушать партнёра; формулировать, аргументировать и отстаивать своё мнение;
формирования учебной и общепользовательской компетентности в области использования информационно-коммуникационных технологий (ИКТ-компетентности);
первоначального представления об идеях и о методах математики как об универсальном языке науки и техники;
развития способности видеть математическую задачу в других дисциплинах, в окружающей жизни;
умения находить в различных источниках информацию, необходимую для решения математических проблем, и представлять её в понятной форме; принимать решение в условиях неполной и избыточной, точной и вероятностной информации;
умения понимать и использовать математические средства наглядности (рисунки, чертежи, схемы и др.) для иллюстрации, интерпретации, аргументации;
умения выдвигать гипотезы при решении учебных задач и понимания необходимости их проверки;
понимания сущности алгоритмических предписаний и умения действовать в соответствии с предложенным алгоритмом;
умения самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем;
способности планировать и осуществлять деятельность, направленную на решение задач исследовательского характера;
предметные:
умения работать с математическим текстом (структурирование, извлечение необходимой информации), точно и грамотно выражать свои мысли в устной и письменной речи, применяя математическую терминологию и символику, использовать различные языки математики (словесный, символический, графический), развития способности обосновывать суждения, проводить классификацию;
владения базовым понятийным аппаратом: иметь представление о числе, дроби, процентах, об основных геометрических объектах (точка, прямая, ломаная, угол, многоугольник, многогранник, круг, окружность, шар, сфера и пр.), формирования представлений о статистических закономерностях в реальном мире и различных способах их изучения;
умения выполнять арифметические преобразования рациональных выражений, применять их для решения учебных математических задач и задач, возникающих в смежных учебных предметах;
умения пользоваться изученными математическими формулами;
знания основных способов представления и анализа статистических данных; умения решать задачи с помощью перебора всех возможных вариантов;
умения применять изученные понятия, результаты и методы при решении задач из различных разделов курса, в том числе задач, не сводящихся к непосредственному применению известных алгоритмов.
Календарно – тематическое планирование уроков алгебры в 7 классе
По учебнику Макарычева Ю.Н., Москва, Просвещение, 2016г.
Количество часов в год – 102
Количество часов в неделю – 3 часа
Количество контрольных работ – 10
| № урока |
| Тема урока | Тип урока | Дата проведения | |
| план | факт | ||||
|
| |||||
| 1/1 | §1 Выражения | Числовые выражения. | Урок открытия новых знаний |
|
|
| 2/2 | Выражения с переменными. | Урок открытия новых знаний |
|
| |
| 3/3 | Нахождение значений выражений с переменными. | Урок рефлексии |
|
| |
| 4/4 | Сравнение значений выражений. | Урок рефлексии |
|
| |
| 5/5 | § 2 Преобразования выражений | Свойства действий над числами | Урок открытия новых знаний |
|
|
| 6/6 | Тождества. | Урок открытия новых знаний |
|
| |
| 7/7 | Тождественные преобразования выражений. | Урок рефлексии |
|
| |
| 8/8 | Обобщающий урок по теме «Числовые и алгебраические выражения» | Урок методологической направленности |
|
| |
| 9/9 | Контрольная работа №1 по теме «Числовые и алгебраические выражения» | Урок развивающего контроля |
|
| |
| 10/10 | § 3 Уравнения с одной переменной | Уравнение и его корни. | Урок открытия новых знаний |
|
|
| 11/11 | Линейное уравнение с одной переменной. | Урок открытия новых знаний |
|
| |
| 12/12 | Решение линейных уравнений. | Урок рефлексии |
|
| |
| 13/13 | Отработка навыков решения линейных уравнений | Урок рефлексии |
|
| |
| 14/14 | Решение задач с помощью уравнений | Урок рефлексии |
|
| |
| 15/15 | Отработка навыков решения задач с помощью уравнений | Урок рефлексии |
|
| |
| 16/16 | Обобщающий урок по теме «Уравнения с одной переменной» | Урок методологической направленности |
|
| |
| 17/17 | Контрольная работа№2 по теме «Уравнения с одной переменной» | Урок развивающего контроля |
|
| |
| 18/18 | § 4 Статистические характеристики | Среднее арифметическое, размах, мода | Урок открытия новых знаний |
|
|
| 19/19 | Отработка навыков вычисления среднего арифметического, размаха, моды | Урок открытия новых знаний |
|
| |
| 20/20 | Медиана как статистическая характеристика | Урок открытия новых знаний |
|
| |
| 21/21 | Формулы | Урок открытия новых знаний |
|
| |
| 2. Функции. (11часов)
| |||||
| 22/1 | §5 Функции и их графики | Что такое функция. | Урок открытия новых знаний |
|
|
| 23/2 | Вычисление значений функции по формуле. | Урок рефлексии |
|
| |
| 24/3 | Нахождение значений функции. | Урок рефлексии |
|
| |
| 25/4 | График функции. | Урок открытия новых знаний |
|
| |
| 26/5 | Построение графика функции. | Урок рефлексии |
|
| |
| 27/6 | §6 Линейная функция | Прямая пропорциональность. | Урок открытия новых знаний |
|
|
| 28/7 | График прямой пропорциональности. | Урок рефлексии |
|
| |
| 29/8 | Линейная функция и ее график. | Урок открытия новых знаний |
|
| |
| 30/9 | Построение графиков линейной функции. | Урок рефлексии |
|
| |
| 31/10 | Обобщающий урок по теме "Функции" | Урок методологической направленности |
|
| |
| 32/11 | Контрольная работа№3 по теме «Понятие функции. Линейная функция и ее график» | Урок развивающего контроля |
|
| |
|
| |||||
| 33/1 | §7 Степень и ее свойства | Определение степени с натуральным показателем | Урок открытия новых знаний |
|
|
| 34/2 | Умножение и деление степеней | Урок открытия новых знаний |
|
| |
| 35/3 | Возведение в степень произведения и степени | Урок открытия новых знаний |
|
| |
| 36/4 | Отработка навыков возведение в степень произведения и степени | Урок рефлексии |
|
| |
| 37/5 |
§8 Одночлены | Одночлен и его стандартный вид. | Урок открытия новых знаний |
|
|
| 38/6 | Умножение одночленов. | Урок открытия новых знаний |
|
| |
| 39/7 | Возведение одночлена в степень. | Урок открытия новых знаний |
|
| |
| 40/8 | Функция y = x² и ее график. | Урок открытия новых знаний |
|
| |
| 41/9 | Функция y = x3 и ее график. | Урок открытия новых знаний |
|
| |
| 42/10 | Обобщение изученного материала по теме «Одночлены» | Урок методологической направленности |
|
| |
| 43/11 | Контрольная работа№4 по теме «Степень с натуральным показателем и ее свойства. Одночлены» | Урок развивающего контроля |
|
| |
| Глава 4. Многочлены. (20 часов)
| |||||
| 44/1 | §9 Сумма и разность многочленов | Многочлен и его стандартный вид. | Урок открытия новых знаний |
|
|
| 45/2 | Сложение и вычитание многочленов. | Урок открытия новых знаний |
|
| |
| 46/3 | Отработка навыков сложения и вычитания многочленов | Урок рефлексии |
|
| |
| 47/4 | Отработка навыков сложения и вычитания многочленов | Урок рефлексии |
|
| |
| 48/5 | §10 Произведение одночлена на многочлен | Умножение одночлена на многочлен. | Урок открытия новых знаний |
|
|
| 49/6 | Использование умножения одночлена на многочлен при преобразовании алгебраических выражений | Урок рефлексии |
|
| |
| 50/7 | Использование умножения одночлена на многочлен при решении уравнений | Урок рефлексии |
|
| |
| 51/8 | Использование умножения одночлена на многочлен при решении задач | Урок рефлексии |
|
| |
| 52/9 | Вынесение общего множителя за скобки. | Урок открытия новых знаний |
|
| |
| 53/10 | Разложение многочлена на множители. | Урок рефлексии |
|
| |
| 54/11 | Контрольная работа№5 по теме « Сумма и разность многочленов. Умножение одночлена на многочлен» | Урок развивающего контроля |
|
| |
| 55/12 |
§11 Произведение многочленов | Умножение многочлена на многочлен. | Урок открытия новых знаний |
|
|
| 56/13 | Представление выражений в виде многочлена. | Урок рефлексии |
|
| |
| 57/14 | Отработка навыков умножения многочлена на многочлен. | Урок рефлексии |
|
| |
| 58/15 | Коррекция навыков умножения многочлена на многочлен | Урок рефлексии |
|
| |
| 59/16 | Разложение многочлена на множители способом группировки. | Урок открытия новых знаний |
|
| |
| 60/17 | Разложение многочлена на множители способом группировки. | Урок рефлексии |
|
| |
| 61/18 | Отработка навыков разложения многочлена на множители способом группировки. | Урок рефлексии |
|
| |
| 62/19 | Обобщение изученного материала по теме «Произведения многочленов» | Урок методологической направленности |
|
| |
| 63/20 | Контрольная работа№6 по теме « Произведение многочленов» | Урок развивающего контроля |
|
| |
| Глава 5. Формулы сокращенного умножения. (18 часов) | |||||
| 64/1 | §12 Квадрат суммы и квадрат разности | Возведение в квадрат и куб суммы и разности двух выражений. | Урок открытия новых знаний |
|
|
| 65/2 | Преобразование выражений. | Урок рефлексии |
|
| |
| 66/3 | Упрощение выражений. | Урок рефлексии |
|
| |
| 67/4 | Разложение на множители с помощью формул квадрата суммы и квадрата разности. | Урок рефлексии |
|
| |
| 68/5 | Преобразование выражений в квадрат двучлена. | Урок рефлексии |
|
| |
| 69/6 |
§13 Разность квадратов. Сумма и разность кубов | Умножение разности выражений на их сумму. | Урок открытия новых знаний |
|
|
| 70/7 | Отработка навыков умножения разности двух выражений на их сумму | Урок рефлексии |
|
| |
| 71/8 | Разложение разности квадратов на множители. | Урок рефлексии |
|
| |
| 72/9 | Разложение разности квадратов на множители. | Урок рефлексии |
|
| |
| 73/10 | Разложение на множители суммы и разности кубов. | Урок рефлексии |
|
| |
| 74/11 | Обобщение изученного материала по теме «Формулы сокращенного умножения» | Урок методологической направленности |
|
| |
| 75/12 | Контрольная работа№7 по теме « Формулы сокращенного умножения» | Урок развивающего контроля |
|
| |
| 76/13 | §14 Преобразование целых выражений | Преобразование целого выражения в многочлен. | Урок открытия новых знаний |
|
|
| 77/14 | Преобразование выражений. | Урок рефлексии |
|
| |
| 78/15 | Применение различных способов для разложения на множители. | Урок рефлексии |
|
| |
| 79/16 | Разложение на множители способом группировки. | Урок рефлексии |
|
| |
| 80/17 | Обобщение изученного материала по теме «Преобразования целых выражений» | Урок методологической направленности |
|
| |
| 81/18 | Контрольная работа№8 по теме «Преобразования целых выражений» | Урок развивающего контроля |
|
| |
| Глава 6. Системы линейных уравнений. (14 часов)
| |||||
| 82/1 | §15Линейные ур-я с двумя переменными | Линейное уравнение с двумя переменными. | Урок открытия новых знаний |
|
|
| 83/2 | График линейного уравнения с двумя переменными. | Урок открытия новых знаний |
|
| |
| 84/3 | Построение графиков линейного уравнения с двумя переменными. | Урок рефлексии |
|
| |
| 85/4 | Системы линейных уравнений с двумя переменными. | Урок рефлексии |
|
| |
| 86/5 | Графический способ решения систем линейных уравнений. | Урок рефлексии |
|
| |
| 87/6 | §16 Решение систем линейных уравнений | Способ подстановки. | Урок открытия новых знаний |
|
|
| 88/7 | Решение систем способом подстановки. | Урок рефлексии |
|
| |
| 89/8 | Способ сложения. | Урок открытия новых знаний |
|
| |
| 90/9 | Решение систем способом сложения. | Урок рефлексии |
|
| |
| 91/10 | Решение задач с помощью систем уравнений. | Урок рефлексии |
|
| |
| 92/11 | Решение задач с помощью систем уравнений. | Урок рефлексии |
|
| |
| 93/12 | Отработка навыков решения задач с помощью систем уравнений | Урок рефлексии |
|
| |
| 94/13 | Обобщение изученного материала по теме « Системы линейных уравнений» | Урок методологической направленности |
|
| |
| 95/14 | Контрольная работа№9 по теме «Системы линейных уравнений» | Урок развивающего контроля |
|
| |
| Итоговое повторение материала (7часов)
| |||||
| 96/1 | Функции | Урок методологической направленности |
|
| |
| 97/2 | Одночлены. Многочлены | Урок методологической направленности |
|
| |
| 98/3 | Формулы сокращенного умножения | Урок методологической направленности |
|
| |
| 99/4 | Системы линейных уравнений | Урок методологической направленности |
|
| |
| 100/5 | Контрольная работа № 10 (итоговая) | Урок развивающего контроля |
|
| |
| 101/6 | Анализ контрольной работы. Решение задач | Урок методологической направленности |
|
| |
| 102/7 | Урок занимательной математики | Урок методологической направленности |
|
| |
Приложение к рабочей программе
Контрольные работы по математике. Блок «Алгебра»
Контрольная работа №1 по теме «Числовые и алгебраические выражения»
1 вариант
Найдите значение выражения: 4а + 6в при а =
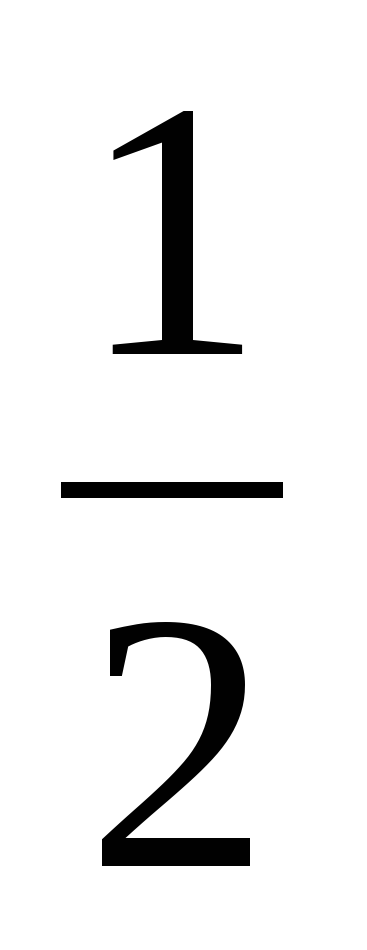 , в =
, в = 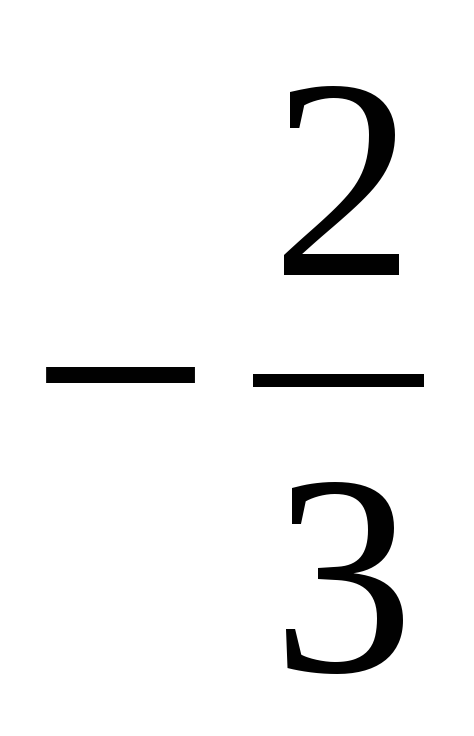 .
.Сравните значения выражений 3х + 0,1 и – 3х – 0,1 при х = – 2.
Упростите выражение: а) 4а – 5в – 2а + 2в; б) 4(3а + 2) – 8; в) 18х – (х – 2) + (2х + 2).
Упростите выражение и найдите его значение: 4 (1,5а – 2,5) – 4а + 8 при а =
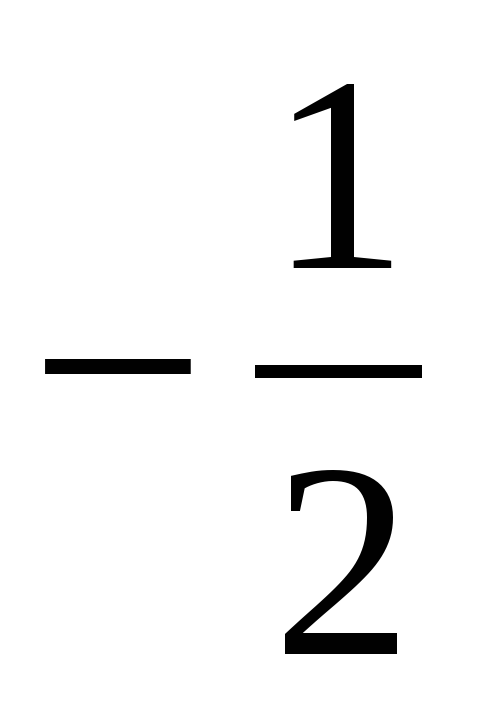
Упростите выражение: 2х – (5х – (4х + 5)).
2 вариант
Найдите значение выражения: 3х – 15у при х =
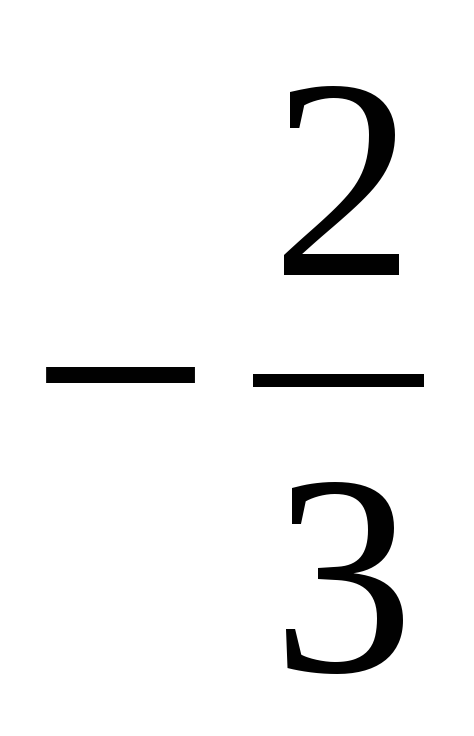 , у =
, у = 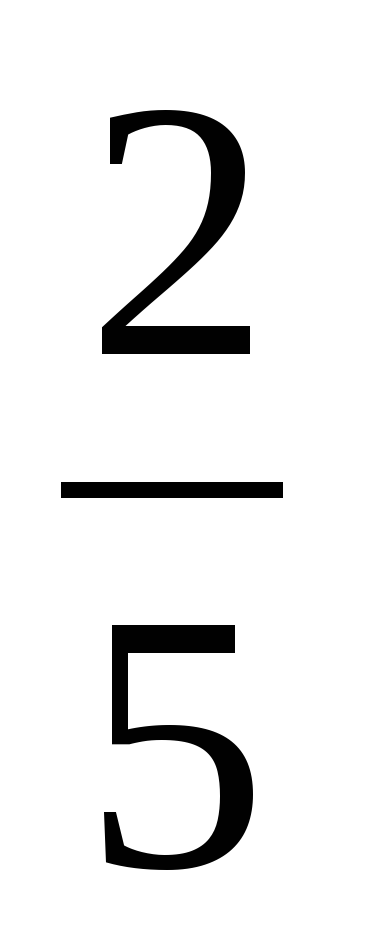 .
.Сравните значения выражений 4 - 0,1а и 0,1а – 4 при а = 2.
Упростите выражение: а) 8х – 5у – 6х + 2у; б) 2(7х – 3)+ 6; в) 13а – (а – 3) + (4а + 3).
Упростите выражение и найдите его значение: – 2 (3х + 2,5)+ 8х + 4 при х =
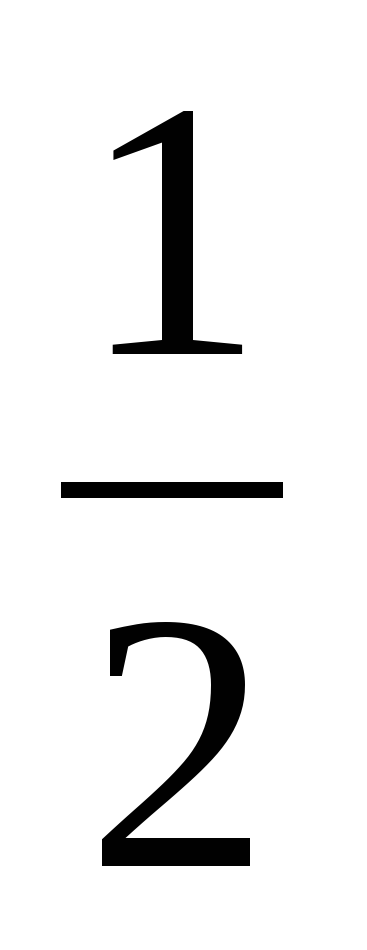
Упростите выражение: 2а – (6а – (3а + 5)).
Контрольная работа№2 по теме «Уравнения с одной переменной»
1 вариант
Решите уравнение: а)
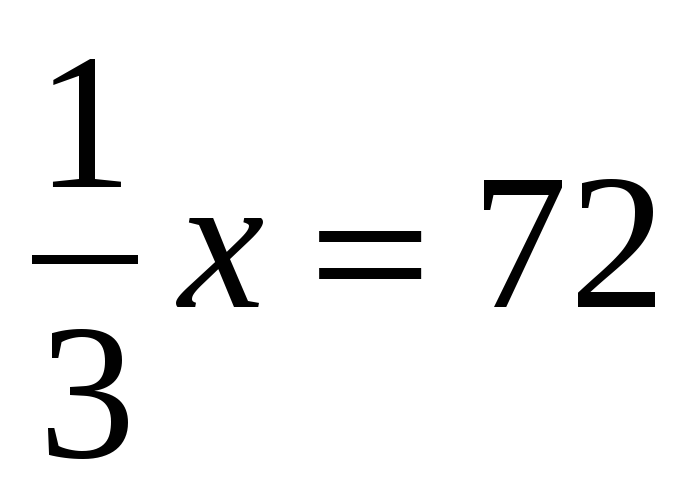 ; б) 6х – 10,2 = 0; в) 5х – 4,5 = 3х + 2,5; г) 2х – (6х – 5) = 45.
; б) 6х – 10,2 = 0; в) 5х – 4,5 = 3х + 2,5; г) 2х – (6х – 5) = 45.Часть пути в школу Таня проезжает на автобусе, а остальной путь проделывает пешком. Вся дорога у нее занимает 26 мин. Она идет на 6 мин дольше, чем едет на автобусе. Сколько минут она едет на автобусе?
В двух сараях сложено сено, причем в первом сарае сена в 3 раза больше, чем во втором. После того как из первого сарая увезли 20 т сена, а во второй привезли 10 т, в обоих сараях сена стало поровну. Сколько тонн сена было в двух сараях первоначально?
Решите уравнение: 7х – (х + 3) = 3(2х – 1)
2 вариант
Решите уравнение: а)
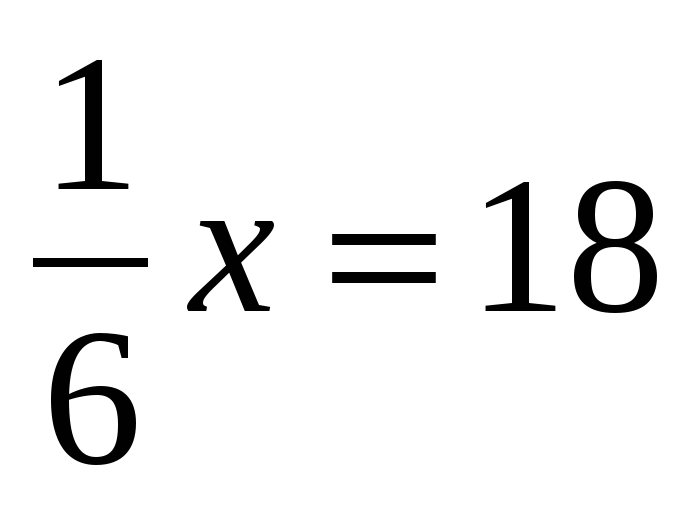 ; б) 7х + 11,9 = 0; в) 6х – 0,8 = 3х + 2,2; г) 5х – (7х + 7) = 9.
; б) 7х + 11,9 = 0; в) 6х – 0,8 = 3х + 2,2; г) 5х – (7х + 7) = 9.Часть пути в 600 км турист пролетел на самолете, а часть проехал на автобусе. На самолете он проделал путь в 9 раз больший, чем на автобусе. Сколько километров проехал турист на автобусе?
На первом участке было в 5 раз больше саженцев смородины, чем на втором. После того как с первого участка увезли 50 саженцев, а на второй посадили еще 90, на обоих участках саженцев стало поровну. Сколько саженцев смородины было на двух участках первоначально?
Решите уравнение: 6х – (2х – 5) = 2(2х + 4)
Контрольная работа№3 по теме «Понятие функции. Линейная функция и ее график»
1 вариант
Функция задана формулой у = 6х +19. Определите: а) значение у, если х = 0,5; б) значение х, при котором у = 1; в) проходит ли график функции через точку А (– 2; 7).
а) постройте график функции у = 2х – 4.б) укажите, чему равно значение у при х = 1,5; при х = 2.
В одной и той же системе координат постройте графики функций: а) у = – 2х ; б) у = 3.
Найдите координаты точки пересечения графиков функций у = 2х – 7 и у = –13х + 23.
Задайте формулой линейную функцию, график которой параллелен прямой у = 3х – 7 и проходит через начало координат.
2 вариант
Функция задана формулой у = 4х – 30. Определите: а) значение у, если х = – 2,5 ; б) значение х, при котором у = – 6; в) проходит ли график функции через точку А (7;– 3).
а) постройте график функции у = – 3х + 3.б) укажите, при каком значении х значение у равно 6; 3.
В одной и той же системе координат постройте графики функций: а) у =
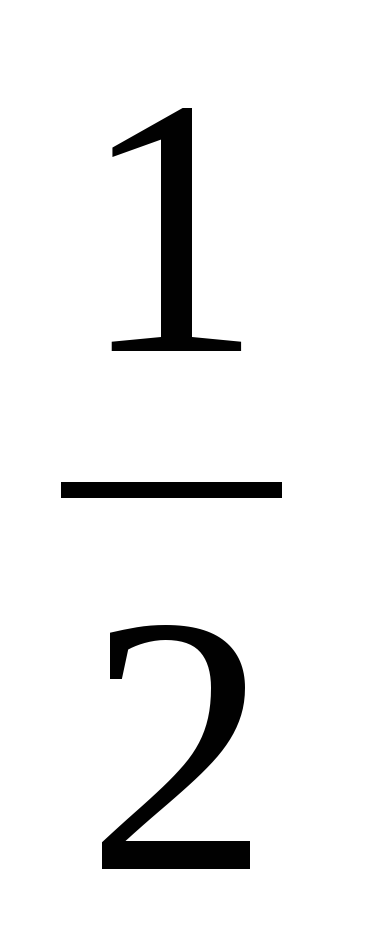 х; б) у = – 4.
х; б) у = – 4.Найдите координаты точки пересечения графиков функций у = 8х + 15 и у = 20х – 9.
Задайте формулой линейную функцию, график которой параллелен прямой у = – 5х + 8 и проходит через начало координат.
Контрольная работа№4 по теме «Степень с натуральным показателем и ее свойства. Одночлены»
1 вариант
Найдите значение выражения: а) 8 ·
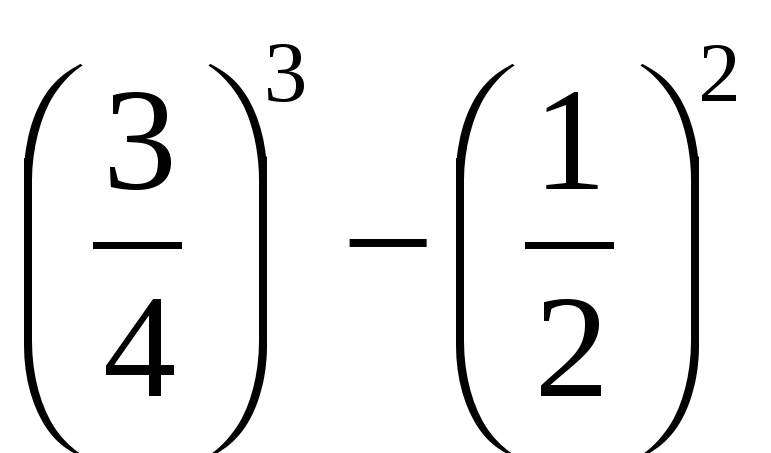 ; б) 1 – 5х2 при х = – 4.
; б) 1 – 5х2 при х = – 4. Выполните действия: а) у7 · у12; б) у20 : у 5; в) (у2)8; г) (2у)4.
Упростите выражение: а) –2ав3·3а2в4; б) (-2а5в2) 3.
Вычислите: а)
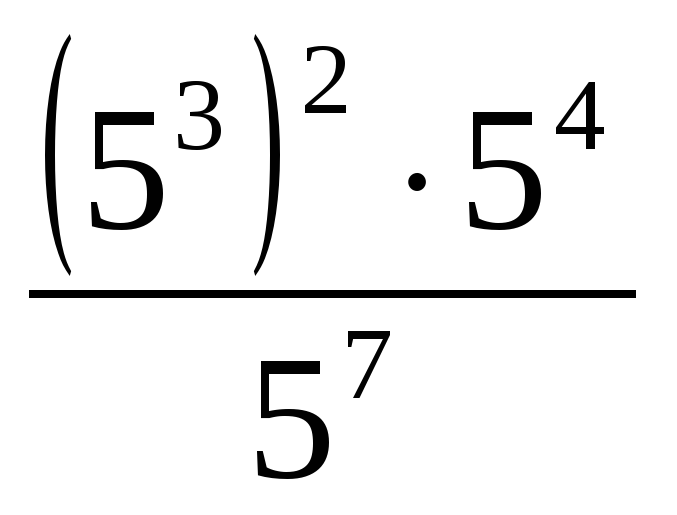 ; б)
; б) 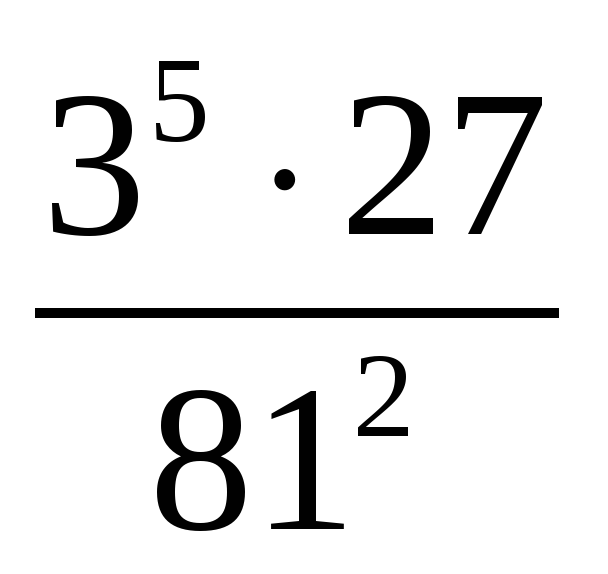 .
.Упростите выражение:
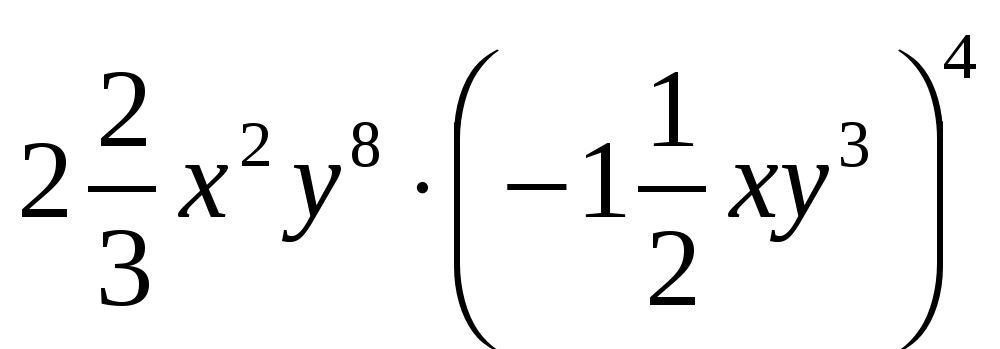 .
.Представьте выражение в виде степени: а) хn-1 · x3-n · x; б) (аn+1)2 : an .
2 вариант
Найдите значение выражения: а) 3 ·
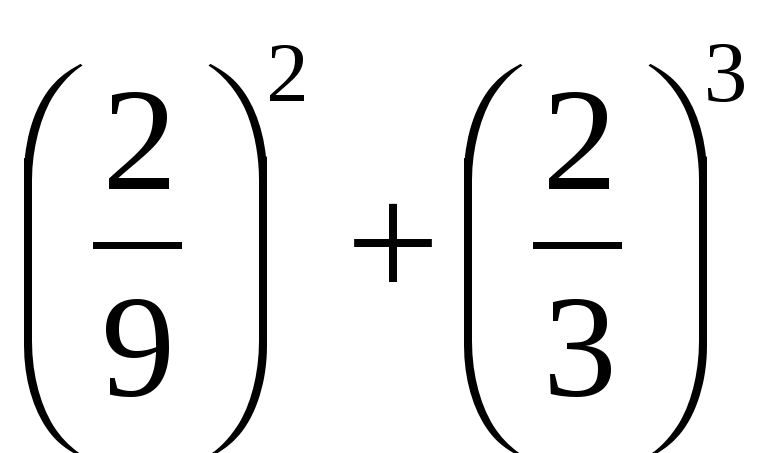 ; б) – 9 p3 при p = –
; б) – 9 p3 при p = –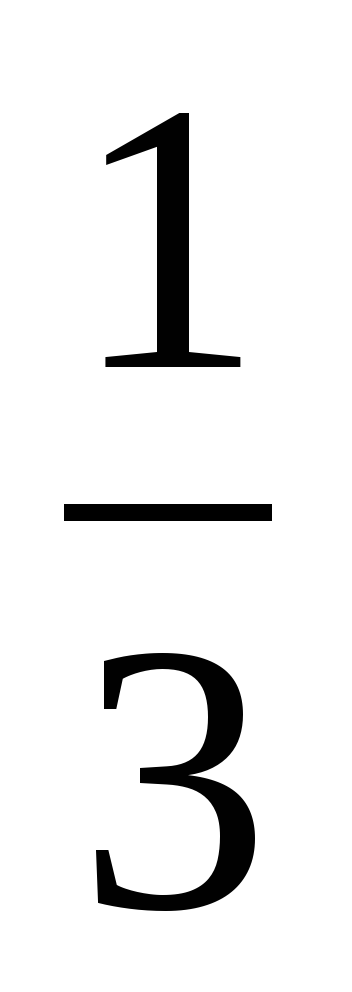 .
.
Выполните действия: а) с3 ·с 22; б) с18 : с 6; в) (с4)6; г) (3с)5.
Упростите выражение: а) –2х5у2 ·3ху4; б) (3х2у3) 2.
Вычислите: а)
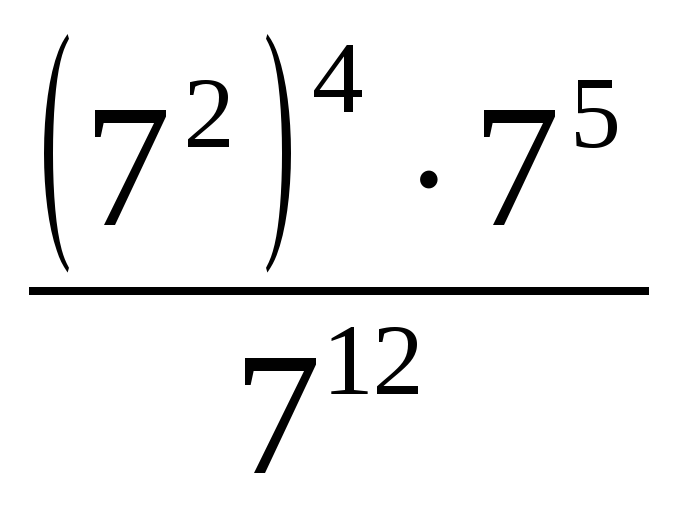 ; б)
; б) 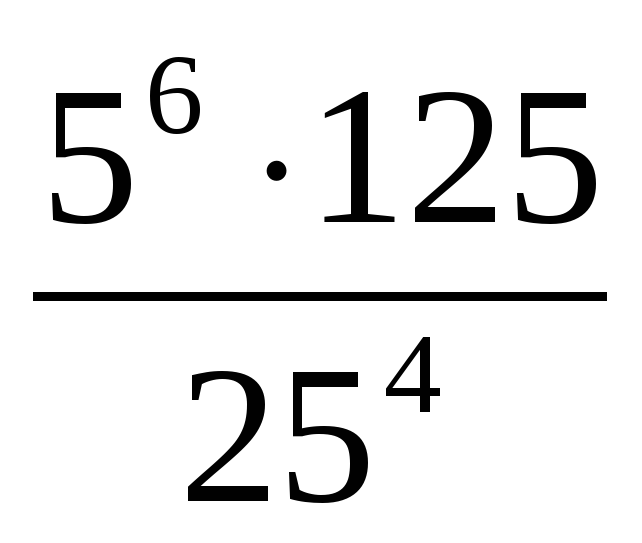 .
.Упростите выражение:
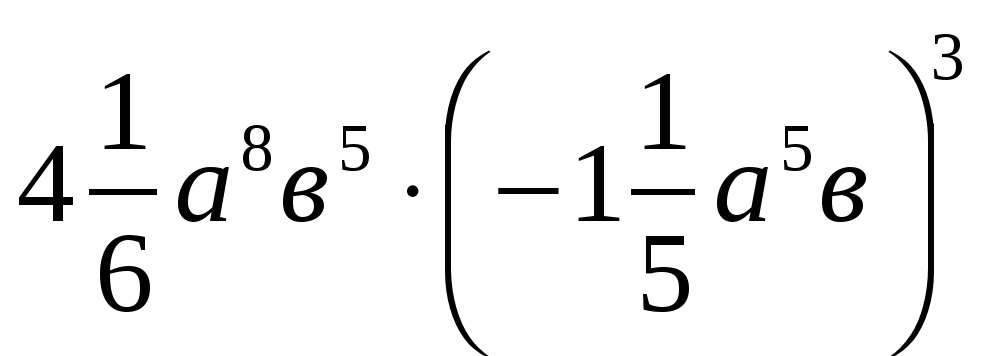 .
.Представьте выражение в виде степени: а) аm+1 ·a ·a3 – m ; б) x 3n : (xn - 1)2 .
Контрольная работа№5 по теме « Сумма и разность многочленов. Умножение одночлена на многочлен»
1 вариант
1. Постройте график функции у = х². С помощью графика функции определите:
а) значение у при х = 1,5; х = - 1,5; б) при каких значениях х значение у равно 4.
2. Округлите число 36,72 до десятых.
Найдите: а) абсолютную погрешность приближения, б) относительную погрешность приближения.
3. По графику функции у = х² (смотри задание №1) найдите приближенное значение у при х = 1,7. Оцените
относительную погрешность приближенного значения.
2 вариант
1. Постройте график функции у = х². С помощью графика функции определите:
а) значение у при х = 2,5; х = -- 2,5 б) при каких значениях х значение у равно 9.
2. Округлите число 5,36 до десятых.
Найдите: а) абсолютную погрешность приближения, б) относительную погрешность приближения.
3. По графику функции у = х² (смотри задание №1) найдите приближенное значение у при х = --1,3. Оцените
относительную погрешность приближенного значения.
Контрольная работа№6 по теме « Произведение многочленов»
1 вариант
1. Выполните действия: а) (3а – 4ах + 2) – (11а – 14 ах); б) 3у2 (у3 + 1).
2. Вынесите общий множитель за скобки: а) 10ав – 15в2; б) 18а3 + 6а2.
3. Решите уравнение: 9х – 6 (х – 1) = 5 (х + 2).
4. За 4 ч пассажирский поезд прошел то же расстояние, что товарный – за 6ч. Найдите скорость пассажирского поезда, если известно, что скорость товарного на 20 км/ч меньше.
5. Решите уравнение: 3х _ х_ 5 – х
6 3 9
6. Упростите выражение: 2а (а + в – с) – 2в (а – в – с) + 2с (а – в + с)
1 вариант
1. Выполните действия: а) (2а2 – 3а + 1) – (7а2 – 5а); б) 3х (4х4 – х).
2. Вынесите общий множитель за скобки: а) 2ху – 3ху2; б) 8в4 + 2в3.
3. Решите уравнение: 7 – 4 (3х – 1) = 5 (1 – 2х).
4.В трех шестых классах 91 ученик. В шестом «А» на 2 ученика меньше, чем в шестом «Б», а в шестом «В» на 3 ученика больше, чем в шестом «Б». Сколько учащихся в каждом классе?
5. Решите уравнение: х – 1 5 – х _ _ 3 х
5 2 4
6. Упростите выражение: 3х (х + у + с) – 3у (х – у – с) – 3с (х + у – с).
Контрольная работа№7 по теме « Формулы сокращенного умножения»
1 вариант
1. Выполните умножение: а) (с + 2) (с – 3); б) (2а – 1) (3а + 4); в) (5х – 2у) (4х – у);
2. Разложите на множители: а) а (а + 3) – 2 (а + 3); б) ах – ау + 5х – 5у ;
3. Упростите выражение: – 0,1 х (2х2 + 6) (5 – 4 х2)
4. Представьте многочлен в виде произведения: а) х2 – ху – 4х + 4у ; б) аb – ас – bх + сх + с – b
5. Из прямоугольного листа железа вырезали квадратную пластинку, для чего с одной стороны листа отрезали полосу шириной 2 см, а с другой – 3 см. Найдите сторону получившегося квадрата, если известно, что его площадь на 51 см2 меньше площади прямоугольника.
2 вариант
1. Выполните умножение: а) (а – 5) (а – 3); б) (5х + 4) (2х – 1); в) (3p – с) (2p + 4с);
2. Разложите на множители: а) х (х – у) + а (х – у); б) 2а – 2b + са – сb ;
3. Упростите выражение: 0,5 (4х2 – 1) (5х2 + 2);
4. Представьте многочлен в виде произведения: а) 2а – ас – 2с + с2 ; б) bх + bу – х – у – ах – ау;
5. Бассейн имеет прямоугольную форму. Одна из его сторон на 6 м больше другой. Вокруг него проходит дорожка, ширина которой 0,5 м. Найдите стороны бассейна, если площадь окружающей его дорожки 15 м2 .
Контрольная работа№8 по теме «Преобразования целых выражений»
1 вариант
Преобразуйте в многочлен: а) (у – 2)2 ; в) (5с – 1) (5с + 1); б) (7х + а)2; г) (3а + 2в) (3а – в);
2. Упростите выражение: (а – 9)2 – (81 + 2а)
3. Разложите на множители: а) х2 – 49; б) 25х2 – 10ху + у2;
4. Решите уравнение: (2 – х)2 – х (х +1,5) = 4;
5. Выполните действия: а) (у2 – 2а) (2а + у2); б) (3х3 + х)2 ; в) (2 + с)2 (2 – с)2;
6. Разложите на множители: а) 4х2у2 – 9а4 ; б) 25а2 – (а + 3)2 ; в) 27а3 + в3;
2 вариант
1. Преобразуйте в многочлен: а) (3а + 4)2 ; в) (в + 3) (в – 3); б) (2х – в)2; г) (5у – 2х) (5у + 2х);
2. Упростите выражение: (с + в) (с – в) + 5с2;
3. Разложите на множители: а) 25у2 – а2; б) с2 + 4вс + 4в2;
4. Решите уравнение: 12 – (4 – х)2 = х (3 – х) ;
5. Выполните действия: а) (3х + у2) (3х – у2); б) (а3 – 6а)2 ; в) (а – х)2 (х + а)2;
6. Разложите на множители: а) 100а4 – в2 ; б) 9х2 – (х – 1)2 ; в) х3 + у6;
Контрольная работа№9 по теме « Системы линейных уравнений»
1 вариант
Решите систему уравнений:
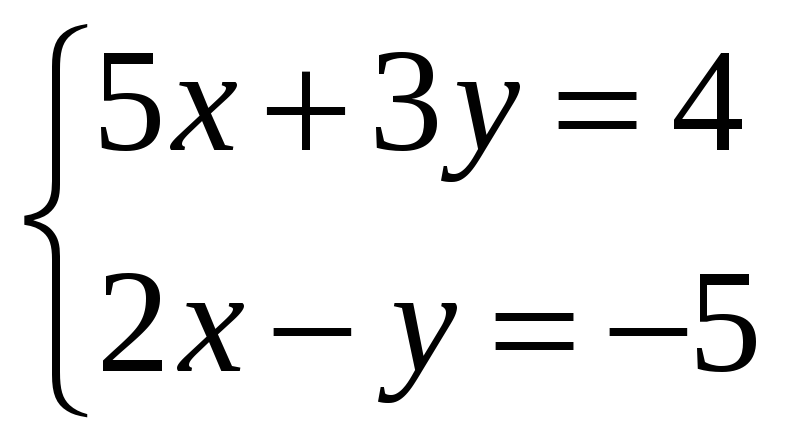 .
.Для седьмого класса купили 30 билетов в театр по 1000 р. И по 1500 р. за билет. За все билеты заплатили 39000 р. Сколько было куплено билетов по 1000 р. И сколько по 1500 р.?
Прямая у = kx + b проходит через точки А (–3; 26) и В (5; –22). Найдите k и b и запишите уравнение этой прямой.
Выясните, имеет ли решения система и сколько:
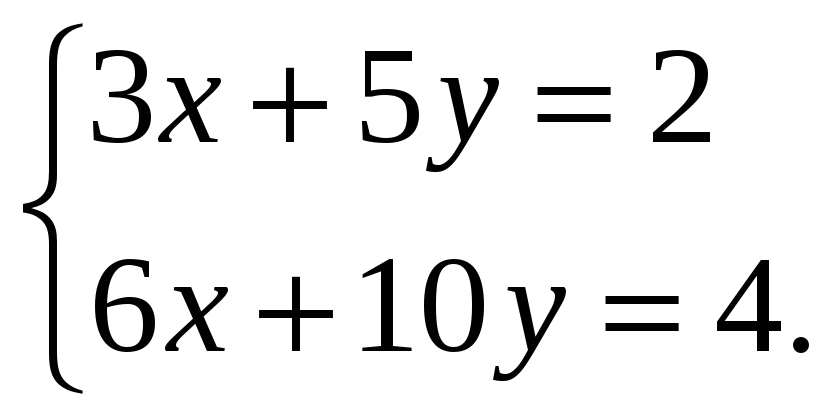
2 вариант
Решите систему уравнений:
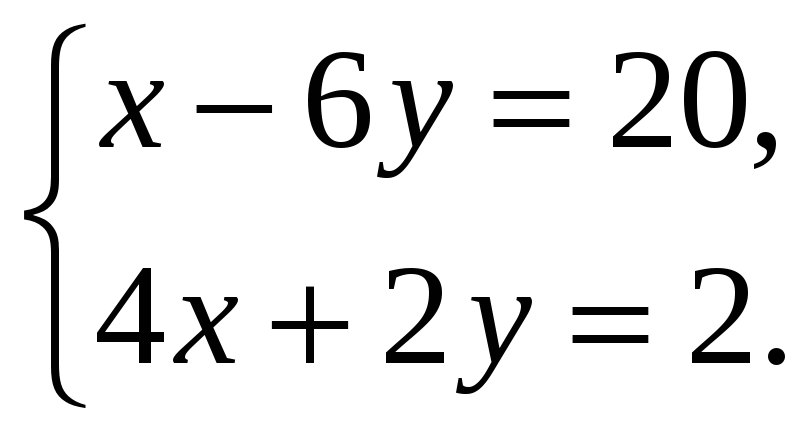
Отряд туристов вышел в поход на 9 байдарках, часть из которых двухместные, а часть – трехместные. Сколько двухместных и сколько трехместных байдарок в походе, если отряд состоит из 23 человек?
Прямая у = kx + b проходит через точки А (6; 7) и В (-2; 11). Найдите k и b и запишите уравнение этой прямой.
Выясните, имеет ли решения система:
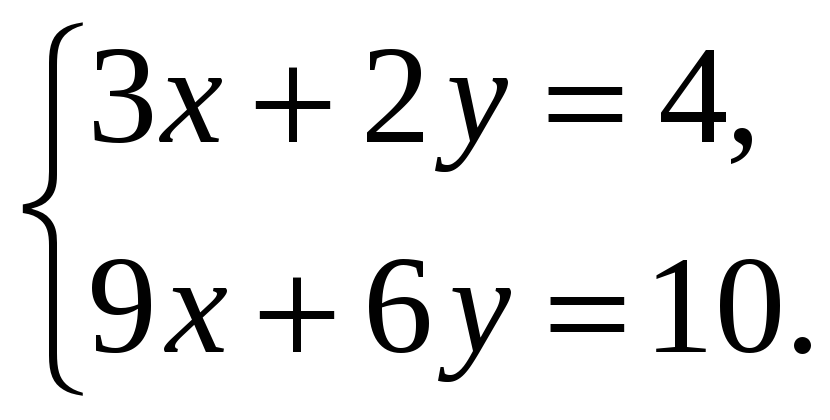
Решите систему уравнений:
Итоговая контрольная работа
1 вариант
1. Найдите значение выражения х3 + 3у2 при х = – 2, у = – 1 .
Решите систему уравнений:
Разложить на множители: а) 2х2 – 8 , б) 3а2 – 3в 2 – а + в .
Велосипедист ехал 2 ч по лесной дороге и 1 ч по шоссе, всего он проехал 40 км. Скорость его на шоссе была на 4 км/ч больше, чем на лесной дороге. С какой скоростью велосипедист ехал по шоссе и с какой скоростью по лесной дороге?
а) Постройте график функции у = 3 – 2х .б) Принадлежит ли графику этой функции точка М (8, – 19) ?
2 вариант
1. Найдите значение выражения а2 + 3в 2 при а = – 3, в = – 2 .
Решите систему уравнений:
Разложить на множители: а) х3 – х , б) х – у – 2х2 + 2у 2 .
Турист ехал 3 ч на автомобиле и 1 ч плыл на лодке, всего он проехал 165 км. Скорость его на автомобиле была на 35 км/ч больше, чем на лодке. С какой скоростью турист ехал на автомобиле и с какой скоростью плыл на лодке?
а) Постройте график функции у = 2 – 3х .б) Принадлежит ли графику этой функции точка А (9, – 25) ?
8

 Получите свидетельство
Получите свидетельство Вход
Вход











 Рабочая программа по алгебре 7 класс (394 KB)
Рабочая программа по алгебре 7 класс (394 KB)
 0
0 887
887 22
22 Нравится
0
Нравится
0





