
по алгебре
среднее общее образование, 10 класс
Учитель. Семенова Елена Николаевна
2016-2017 учебный год
Раздел 1.Пояснительная записка
Данная рабочая образовательная программа ориентирована на учащихся 10 класса (базовый уровень) и реализуется на основе следующих нормативных документов:
Федеральный Закон «Об образовании в Российской Федерации» (от 29.12.2012 №273-ФЗ).
Областной закон от 14.11.2013 № 26-ЗС «Об образовании в Ростовской области» (в ред. от 24.04.2015 № 362-ЗС).
Федеральный компонент государственного стандарта основного общего и среднего (полного) общего образования (Приказ МОиН РФ от 05.03.2004г. № 1089).
Приказ Минобразования России от 09.03.2004 №1312 «Об утверждении федерального базисного учебного плана и примерных учебных планов для образовательных учреждений Российской Федерации, реализующих программы общего образования».
Приказ Минобрнауки России от 31.03.2014 г №253 «Об утверждении федеральных перечней учебников, рекомендованных к использованию при реализации имеющих государственную аккредитацию образовательных программ начального общего, основного общего, среднего общего образования».
Федеральный перечень учебников, рекомендованных Министерством образования и науки Российской Федерации к использованию в образовательном процессе в общеобразовательных учреждениях на 2016/2017 учебный год.
Приказ Министерства общего и профессионального образования Ростовской области № 271 от 18.04.2016 «Об утверждении регионального примерного учебного недельного плана для образовательных организаций, реализующих программы общего образования, расположенных на территории Ростовской области на 2016-2017 учебный год».
Учебный план МБОУ СОШ № 4 г.Новошахтинска на 2016-2017 учебный год
Бурмистрова Т.А. Алгебра и начала математического анализа 10-11 классы. Программы общеобразовательных учреждений. - М: «Просвещение», 2009.
Днепров Э., Аркадьев А. Сборник нормативных документов. -М: Дрофа, 2004
Данная рабочая программа предназначена для работы с УМК Колягина Ю.М, Ткачевой М.В, и др. Алгебра и начала математического анализа. 10 класс. Учебник для общеобразовательных учреждений: базовый и профильный уровни - Москва: «Просвещение», 2011 год и полностью отражает базовый уровень подготовки школьников по разделам программы. Она конкретизирует содержание тем образовательного стандарта и дает примерное распределение учебных часов по разделам курса.
Рабочая программа выполняет две основные функции:
Информационно-методическая функция позволяет всем участникам образовательного процесса получить представление о целях, содержании, общей стратегии обучения, воспитания и развития учащихся средствами данного учебного предмета.
Организационно-планирующая функция предусматривает выделение этапов обучения, структурирование учебного материала, определение его количественных и качественных характеристик на каждом из этапов, в том числе для содержательного наполнения промежуточной аттестации учащихся.
Изучение математики на базовом уровне среднего общего образования направлено на достижение следующих целей:
формирование представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, об идеях и методах математики;
развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне, необходимом для будущей профессиональной деятельности, а также последующего обучения в высшей школе;
овладение математическими знаниями и умениями, необходимыми в повседневной жизни, для изучения школьных естественнонаучных дисциплин на базовом уровне, для получения образования в областях, не требующих углубленной математической подготовки;
воспитание средствами математики культуры личности, понимания значимости математики для научно-технического прогресса, отношения к математике как к части общечеловеческой культуры через знакомство с историей развития математики, эволюцией математических идей.
Целью изучения курса алгебры и начала анализа в 10-11 классах является:
систематическое изучение функций как важнейшего математического объекта средствами алгебры и математического анализа;
раскрытие политехнического и прикладного значения общих методов математики, связанных с исследованием функций;
интеллектуальное развитие, формирование уровня абстрактного и логического мышления и алгоритмической культуры, необходимого для обучения в высшей школе и будущей профессиональной деятельности;
подготовка необходимого аппарата для изучения геометрии и физики.
Общая характеристика предмета
При изучении курса алгебры и начала анализа на базовом уровне продолжаются и получают развитие содержательные линии: «Алгебра», «Функции», «Уравнения и неравенства», «Элементы комбинаторики, теории вероятностей, статистики и логики», вводится линия «Начала математического анализа (11 класс)».
В рамках указанных содержательных линий решаются следующие задачи:
систематизация сведений о числах; изучение новых видов числовых выражений и формул; совершенствование практических навыков и вычислительной культуры, расширение и совершенствование алгебраического аппарата, сформированного в основной школе, и его применение к решению математических и нематематических задач;
расширение и систематизация общих сведений о функциях, пополнение класса изучаемых функций, иллюстрация широты применения функций для описания и изучения реальных зависимостей;
развитие представлений о вероятностно-статистических закономерностях в окружающем мире, совершенствование интеллектуальных и речевых умений путем обогащения математического языка, развития логического мышления.
Место предмета в базисном учебном плане
Согласно Федеральному базисному учебному плану для образовательных учреждений Российской Федерации на изучение алгебры в 10 классе отводится 3 часа в неделю. Продолжительность учебного года составляет 34 учебных недели. Таким образом, курс рассчитан на 102 часа в год, но согласно письму Министерства образования РФ о
рекомендуемых сроках каникул в 2016-2017 учебном году и в соответствии с годовым календарным графиком на 2016-2017 учебный год (учебный год для 10-х классов длится с
1 сентября 2016 по 26 мая 2017г.) будет 101 час (1 четверть – 25 уроков, 2 четверть – 21 урок, 3 четверть – 31 урок, 4 четверть – 24 урока).
Раздел 2. Планируемые результаты освоения предмета «Алгебра и начала анализа» - 10 класс
| Личностные | Метапредметные | ||
| Регулятивные УУД | Познавательные УУД | Коммуникативные УУД | |
|
|
|
|
Предметные
| № п/п | Содержательные линии | Базовый уровень Ученик научится: | Повышенный уровень Ученик получит возможность: |
| 1 | Алгебра |
|
|
| 2 | Функции и графики |
|
|
| 3 | Уравнения и неравенства |
|
|
| 4 | Элементы комбинаторики, статистики и теории вероятности | 1)решать простейшие комбинаторные задачи методом перебора, а также с использованием известных формул; 2)вычислять в простейших случаях вероятности событий на основе подсчета числа исходов; использовать приобретенные знания и умения в практической деятельности и повседневной жизни для анализа реальных числовых данных, представленных в виде диаграмм, графиков; анализа информации статистического характера | 1) овладеть некоторыми специальными приемами решения комбинаторных задач; 2) приобрести опыт проведения случайных экспериментов, интерпретации их результатов |
Раздел 3. Содержание учебного предмета
| № п/п | Название главы (раздела) | Содержание учебного предмета | Основные виды учебной деятельности | Формы организации учебных занятий |
| 1 | Повторение курса алгебры 7-9 классов | Действия с обыкновенными и десятичными дробями. Положительные и отрицательные числа. Модуль числа. Квадратный корень. Разложение многочленов на множители. Алгебраические дроби. Свойства степени с целым показателем. Уравнение с одной переменной. Квадратное уравнение. Рациональное уравнение. Системы уравнений. Неравенства. | Решать линейные, квадратные, алгебраические уравнения; линейные и квадратные неравенства с одной переменной и их системы; описывать свойства изученных функций, строить их графики; применять свойства арифметических квадратных корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни; распознавать арифметические и геометрические прогрессии; решать задачи с применением формулы общего члена и суммы нескольких первых членов |
|
| 2 | Степень с действительным показателем | Целые и рациональные числа. Действительные числа. Бесконечно убывающая геометрическая прогрессия и ее сумма. Корень степени n1 и его свойства. Степень с рациональным показателем и его свойства. Понятие о степени с действительным показателем. Свойства степени с действительным показателем | Иметь представление о расширении множества чисел, свойствах чисел; об обращении периодической десятичной дроби в обыкновенную с помощью бесконечно- убывающей геометрической прогрессии; выполнять арифметические действия с действительными числами; простые преобразования выражений, содержащих арифметический корень; вычислять степень с рациональным и действительным показателем |
|
| 3 | Степенная функция | Функции. Область определения и множество значений. График функции. Построение графиков функций, заданных различными способами. Преобразования графиков: параллельный перенос, симметрия относительно осей координат и симметрия относительно начала координат, симметрия относительно прямой , растяжение и сжатие вдоль осей координат. Свойства функции: монотонность, четность и нечетность, ограниченность. Степенная функция с натуральным показателем, ее свойства и график. Обратная функция. Область определения и область значений обратной функции. График обратной функции. Вертикальные и горизонтальные асимптоты графиков. Графики дробно – линейных функций. Равносильность уравнений и неравенств. Решение иррациональных уравнений | Иметь наглядное представления об основных свойствах функций; изображать графики степенной функции; описывать свойства этих функций, опираясь на график; решать иррациональные уравнения и неравенства, используя стандартный алгоритм их решения |
|
| 4 | Показательная функция | Показательная функция, ее свойства и график. Решение показательных уравнений и неравенств и их систем. Основные приемы решения систем уравнений: подстановка, алгебраическое сложение, введение новых переменных. | Иметь наглядное представления об основных свойствах функций, иллюстрировать их с помощью графических изображений; изображать графики показательной функции; описывать свойства этих функций, опираясь на график; использовать свойства функции для сравнения и оценки ее значений; решать показательные уравнения и неравенства, применяя различные методы их решения. |
|
| 5 | Логарифмическая функция | Логарифм числа. Основное логарифмическое тождество. Логарифм произведения, частного, степени; переход к новому основанию. Десятичный и натуральный логарифмы, число e. Преобразование простейших выражений, включающих арифметические операции, операцию возведение в степень и операцию логарифмирования. Логарифмическая функция, ее свойства и график. Решение логарифмических уравнений и неравенств. | Иметь наглядное представления об основных свойствах логарифмических функций, иллюстрировать их с помощью графических изображений; изображать графики логарифмических функций; описывать свойства этих функций, опираясь на график; использовать свойства логарифмической функции для сравнения и оценки ее значений; решать логарифмические уравнения и неравенства, применяя различные методы их решения. |
|
| 6 | Тригонометрические формулы | Радианная мера угла. Синус, косинус, тангенс, котангенс произвольного угла и числа. Основные тригонометрические тождества. Формулы приведения. Синус, косинус и тангенс суммы и разности двух углов. Синус и косинус двойного угла. Формулы половинного угла. Преобразования суммы тригонометрических функций в произведение и произведения в сумму. Выражение тригонометрических функций через тангенс половинного аргумента. Преобразования простейших тригонометрических выражений. | Находить значения синуса косинуса, тангенса угла на основе определений, с помощью калькулятора и таблиц; выполнять тождественные преобразования тригонометрических выражений; применять тригонометрические формулы в при решении практических задач |
|
| 7 | Тригонометрические уравнения | Простейшие тригонометрические уравнения. Решение тригонометрических уравнений. Простейшие тригонометрические неравенства. Арксинус, арккосинус, арктангенс числа. | Решать простейшие тригонометрические уравнения и неравенства; овладеть некоторыми приемами решения тригонометрических уравнений. |
|
| 8 | Повторение
| Действительные числа. Степенная функция, ее свойства и график. Показательная функция, ее свойства и график. Логарифмическая функция, ее свойства и график.
| Производить вычисления с натуральными, целыми, рациональными, действительными числами; обращать бесконечную периодическую дробь в обыкновенную; выполнять преобразования иррациональных, степенных, логарифмических, тригонометрических выражений; решать алгебраические, иррациональные, показательные, логарифмические, тригонометрические уравнения, неравенства и их системы, применяя различные методы их решений; знать свойства степенной, показательной, логарифмической функций и строить их графики и применять свойства функций при решении различных задач. |
|
Тематическое планирование
| № п/п | Название темы | Количество часов | Оценка планируемых результатов |
| 1 | Повторение курса алгебры 7-9 классов | 7 | Входная к.р. |
| 2 | Степень с действительным показателем | 10 | к.р. № 1 |
| 3 | Степенная функция | 12 | к.р. № 2 |
| 4 | Показательная функция | 11 | к.р. № 3 |
| 5 | Логарифмическая функция | 15 | к.р. № 4 |
| 6 | Тригонометрические формулы | 21 | к.р. № 5 |
| 7 | Тригонометрические уравнения | 17 | к.р. № 6 |
| 8 | Повторение | 7 | Итоговый контроль |
|
| ВСЕГО | 101 час |
|
Календарное планирование
| № п/п | Дата | Тема урока | Количество часов |
|
|
| Повторение курса алгебры 7-9 классов Цель – обобщить и систематизировать знания за курс алгебры 7-9 классов | 7 |
| 1 | 02.09 | Алгебраические выражения. | 1 |
| 2 | 07 | Линейная функция. Линейные уравнения и системы уравнений. | 1 |
| 3 | 07 | Числовые неравенства и неравенства с одним неизвестным | 1 |
| 4 | 09 | Квадратные корни. Квадратные уравнения | 1 |
| 5 | 14 | Квадратичная функция. Квадратные неравенства | 1 |
| 6 | 14 | Свойства и графики функций | 1 |
| 7 | 16 | Прогрессии и сложные проценты. Начала статистики | 1 |
|
|
| Степень с действительным показателем Цель – обобщить и систематизировать знания о действительных числах; сформировать понятие степени с действительным показателем; научить применять определения арифметического корня и степени, а также их свойства при выполнении вычислений и преобразовании выражений | 11 |
| 8 | 21 | Действительные числа | 1 |
| 9 | 21 | Бесконечно убывающая геометрическая прогрессия | 1 |
| 10 | 23 | Входной контроль по текстам администрации | 1 |
| 11 | 28 | Формула суммы бесконечно убывающей геометрической прогрессии. | 1 |
| 12 | 28 | Арифметический корень натуральной степени | 1 |
| 13 | 30 | Арифметический корень натуральной степени | 1 |
| 14 | 05.10 | Арифметический корень натуральной степени | 1 |
| 15 | 05 | Степень с рациональным и действительным показателями | 1 |
| 16 | 07 | Степень с рациональным и действительным показателями | 1 |
| 17 | 12 | Степень с рациональным и действительным показателями | 1 |
| 18 | 12 | Контрольная работа № 1 по теме «Степень с действительным показателем» | 1 |
|
|
| Степенная функция Цель- обобщить и систематизировать известные из курса алгебры основной школы свойства функций; изучить свойства степенных функций и научить применять их при решении уравнений и неравенств; сформировать понятие равносильности уравнений, неравенств, систем уравнений и неравенств. |
11 |
| 19 | 14 | Степенная функция, ее свойства и график | 1 |
| 20 | 19 | Свойства степенной функции при различных показателях степеней | 1 |
| 21 | 19 | Взаимно-обратные функции. Построение графиков взаимно-обратных функций | 1 |
| 22 | 21 | Сложная функция. Нахождение области определения сложных функций. | 1 |
| 23 | 26 | Дробно-линейная функция. | 1 |
| 24 | 26 | Равносильные уравнения и неравенства. | 1 |
| 25 | 28 | Равносильные уравнения и неравенства | 1 |
| 26 | 09.11 | Иррациональные уравнения | 1 |
| 27 | 09 | Иррациональные уравнения | 1 |
| 28 | 11 | Иррациональные неравенства | 1 |
| 29 | 16 | Контрольная работа № 2 по теме «Степенная функция» | 1 |
|
|
| Показательная функция Цель - изучить свойства показательной функции; научить решать показательные уравнения и неравенства, системы показательных уравнений | 11 |
| 30 | 16 | Показательная функция, ее свойства и график | 1 |
| 31 | 18 | Показательная функция, ее свойства и график | 1 |
| 32 | 23 | Показательные уравнения | 1 |
| 33 | 23 | Показательные уравнения | 1 |
| 34 | 25 | Показательные уравнения | 1 |
|
|
| Показательные неравенства | 1 |
| 35 | 30 | Показательные неравенства | 1 |
| 36 | 30 | Показательные неравенства | 1 |
| 37 | 02.12 | Системы показательных уравнений и неравенств | 1 |
| 38 | 07 | Системы показательных уравнений и неравенств | 1 |
| 39 | 07 | Контрольная работа № 3 по теме «Показательная функция» | 1 |
|
|
| Логарифмическая функция Цель- сформировать понятие логарифма числа; научить применять свойства логарифмов при решении уравнений; изучить свойства логарифмической функции; научить применять свойства логарифмической функции при решении логарифмических уравнений и неравенств | 15 |
| 40 | 09 | Логарифмы | 1 |
| 41 | 14 | Логарифмы | 1 |
| 42 | 14 | Свойства логарифмов | 1 |
| 43 | 16 | Свойства логарифмов | 1 |
| 44 | 21 | Десятичные и натуральные логарифмы. Формула перехода | 1 |
| 45 | 21 | Десятичные и натуральные логарифмы. Формула перехода | 1 |
| 46 | 23 | Логарифмическая функция, ее свойства и график | 1 |
| 47 | 11.01 | Логарифмическая функция, ее свойства и график | 1 |
| 48 | 11 | Логарифмические уравнения | 1 |
| 49 | 13 | Логарифмические уравнения | 1 |
| 50 | 18 | Логарифмические уравнения | 1 |
| 51 | 18 | Логарифмические неравенства | 1 |
| 52 | 20 | Логарифмические неравенства | 1 |
| 53 | 25 | Логарифмические неравенства повышенной сложности | 1 |
| 54 | 25 | Контрольная работа № 4 по теме «Логарифмическая функция» | 1 |
|
|
| Тригонометрические формулы Цель- сформировать понятие синуса, косинуса, тангенса, котангенса числа; научить применять формулы тригонометрии для вычисления значений тригонометрических функций и выполнения преобразований тригонометрических выражений; научить решать простейшие тригонометрические уравнения sinx = a, cosx = a при а = 1; -1; 0.
| 21 |
| 55 | 27 | Радианная мера угла
| 1 |
| 56 | 01.02 | Поворот точки вокруг начала координат | 1 |
| 57 | 01 | Поворот точки вокруг начала координат | 1 |
| 58 | 03 | Определение синуса, косинуса, тангенса угла | 1 |
| 59 | 08 | Определение синуса, косинуса, тангенса угла | 1 |
| 60 | 08 | Знаки синуса, косинуса и тангенса | 1 |
| 61 | 10 | Зависимость между синусом, косинусом и тангенсом одного и того же угла | 1 |
| 62 | 15 | Зависимость между синусом, косинусом и тангенсом одного и того же угла | 1 |
| 63 | 15 | Тригонометрические тождества | 1 |
| 64 | 17 | Тригонометрические тождества | 1 |
| 65 | 22 | Синус, косинус и тангенс углов ά и –ά. | 1 |
| 66 | 22 | Формулы сложения | 1 |
| 67 | 24 | Формулы сложения | 1 |
| 68 | 01.03 | Синус, косинус и тангенс двойного угла. | 1 |
| 69 | 01 | Синус, косинус и тангенс половинного угла. | 1 |
| 70 | 03 | Формулы приведения | 1 |
| 71 | 10 | Формулы приведения | 1 |
| 72 | 15 | Сумма и разность синусов. Сумма и разность косинусов | 1 |
| 73 | 15 | Сумма и разность синусов. Сумма и разность косинусов | 1 |
| 74 | 17 | Произведение синусов и косинусов | 1 |
| 75 | 22 | Контрольная работа № 5 по теме «Тригонометрические формулы» | 1 |
|
|
| Тригонометрические уравнения Цель- сформировать умение решать простейшие тригонометрические уравнения; ознакомить с некоторыми приёмами решения тригонометрических уравнений | 17 |
| 76 | 22 | Уравнение cos x = a | 1 |
| 77 | 24 | Уравнение cos x = a | 1 |
| 78 | 05.04 | Уравнение sin x = a | 1 |
| 79 | 05 | Уравнение sin x = a | 1 |
| 80 | 07 | Уравнение tg x = a | 1 |
| 81 | 12 | Уравнение tg x = a | 1 |
| 82 | 12 | Тригонометрические уравнения, сводящиеся к алгебраическим | 1 |
| 83 | 14 | Тригонометрические уравнения, сводящиеся к алгебраическим | 1 |
| 84 | 19 | Однородные и линейные уравнения тригонометрические уравнения | 1 |
| 85 | 19 | Однородные и линейные уравнения тригонометрические уравнения | 1 |
| 86 | 21 | Методы замены неизвестного и разложения на множители | 1 |
| 87 | 26 | Методы замены неизвестного и разложения на множители | 1 |
| 88 | 26 | Метод оценки левой и правой частей тригонометрического уравнения | 1 |
| 89 | 28 | Системы тригонометрических уравнений | 1 |
| 90 | 03.05 | Тригонометрические неравенства | 1 |
| 91 | 03 | Контрольная работа № 6 по теме «Тригонометрические уравнения» | 1 |
| 92 | 05 | Решение тригонометрических уравнений | 1 |
| 93 | 10 | Решение тригонометрических уравнений | 1 |
|
|
| Повторение Цель – обобщить и систематизировать знания учащихся | 8 |
| 94 | 10 | Показательные уравнения и неравенства. | 1 |
| 95 | 12 | Логарифмические уравнения и неравенства | 1 |
| 96 и 97 | 17 и 17 | Итоговая контрольная работа по текстам администрации | 2 |
| 98 | 19 | Логарифмические уравнения и неравенства | 1 |
| 99 | 24 | Тригонометрические формулы | 1 |
| 100 | 24 | Тригонометрические уравнения | 1 |
| 101 | 26 | Тригонометрические уравнения | 1 |
Пропустила в журнале 24 февраля
Раздел 4. Контрольно- измерительные материалы
4.1. График проведения контрольных работ в 10 классе по алгебре и началам анализа 2016-2017 уч.г.
| № п/п | Форма и тема контроля | Дата | |
| план | факт | ||
| 1 | Входная контрольная работа по текстам администрации
|
|
|
| 2 | Контрольная работа № 1 по теме «Степень с действительным показателем» |
|
|
| 3 | Контрольная работа № 2 по теме «Степенная функция» |
|
|
| 4 | Контрольная работа №3 по теме «Показательная функция» |
|
|
| 5 | Контрольная работа № 4 по теме "Логарифмическая функция» |
|
|
| 6 | Контрольная работа №5 по теме "Тригонометрические формулы" |
|
|
| 7 | Контрольная работа №6 по теме «Тригонометрические уравнения» |
|
|
| 8 | Итоговая контрольная работа по текстам администрации |
|
|
4.2. Тексты контрольных работ для 10 класса по алгебре и началам анализа 2016-2017 уч.г.
К
 онтрольная работа № 1 по теме «Степень с действительным показателем» Повышенный уровень
онтрольная работа № 1 по теме «Степень с действительным показателем» Повышенный уровень
Контрольная работа № 2 по теме «Степенная функция»
Повышенный уровень
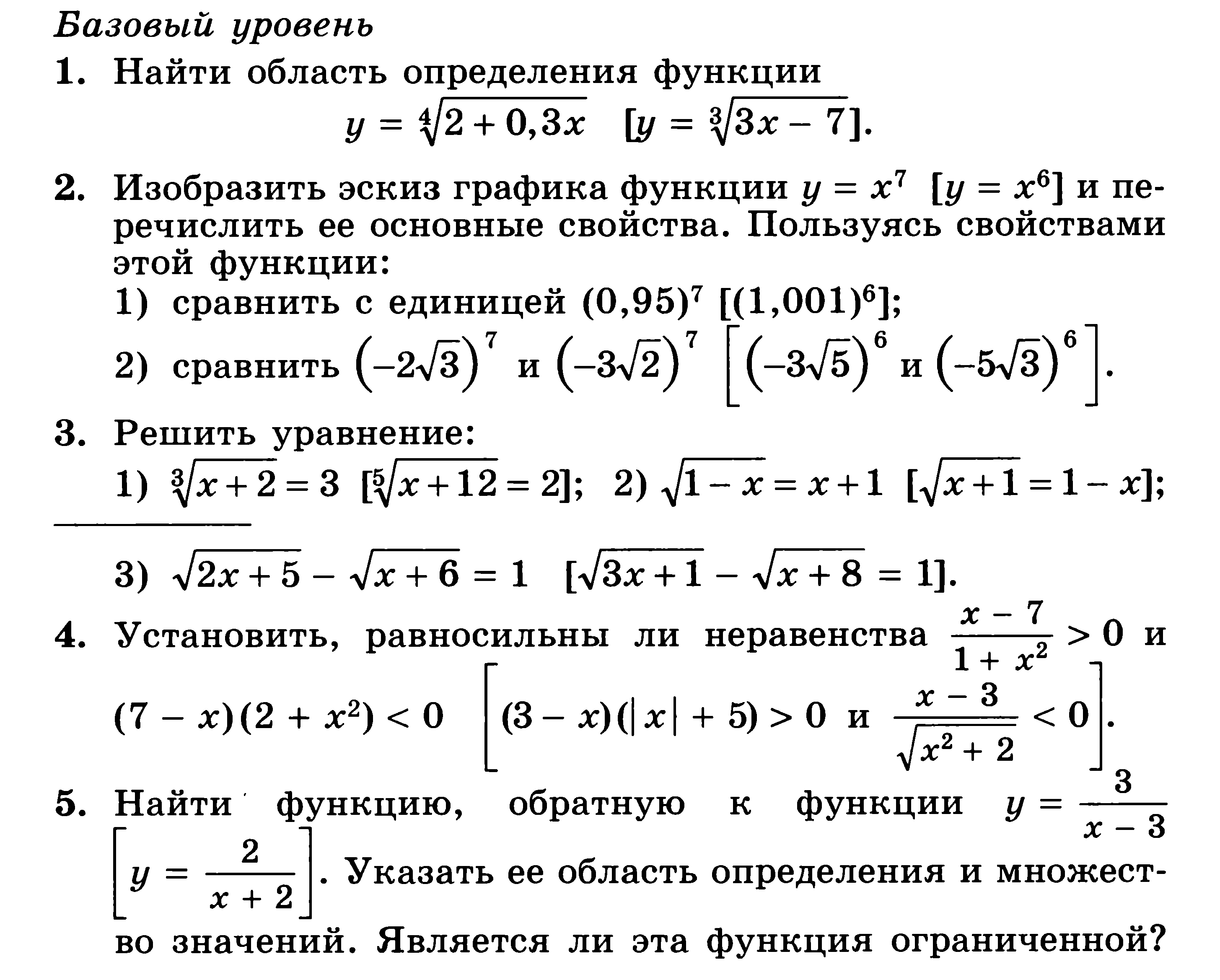

Для 2 варианта задание № 4
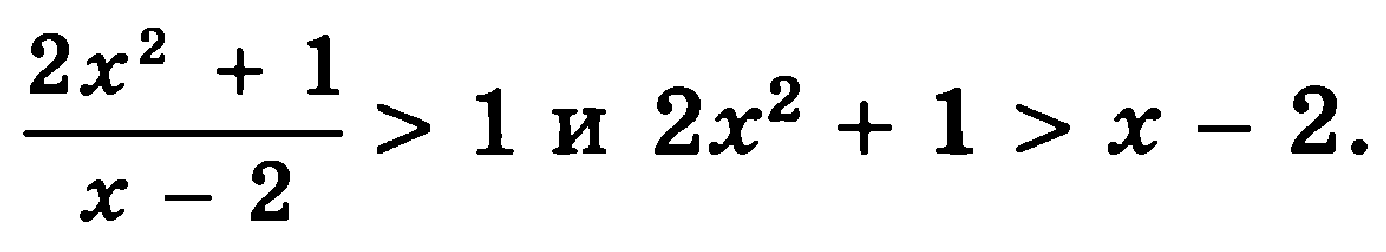
Контрольная работа № 3 по теме «Показательная функция»
Повышенный уровень
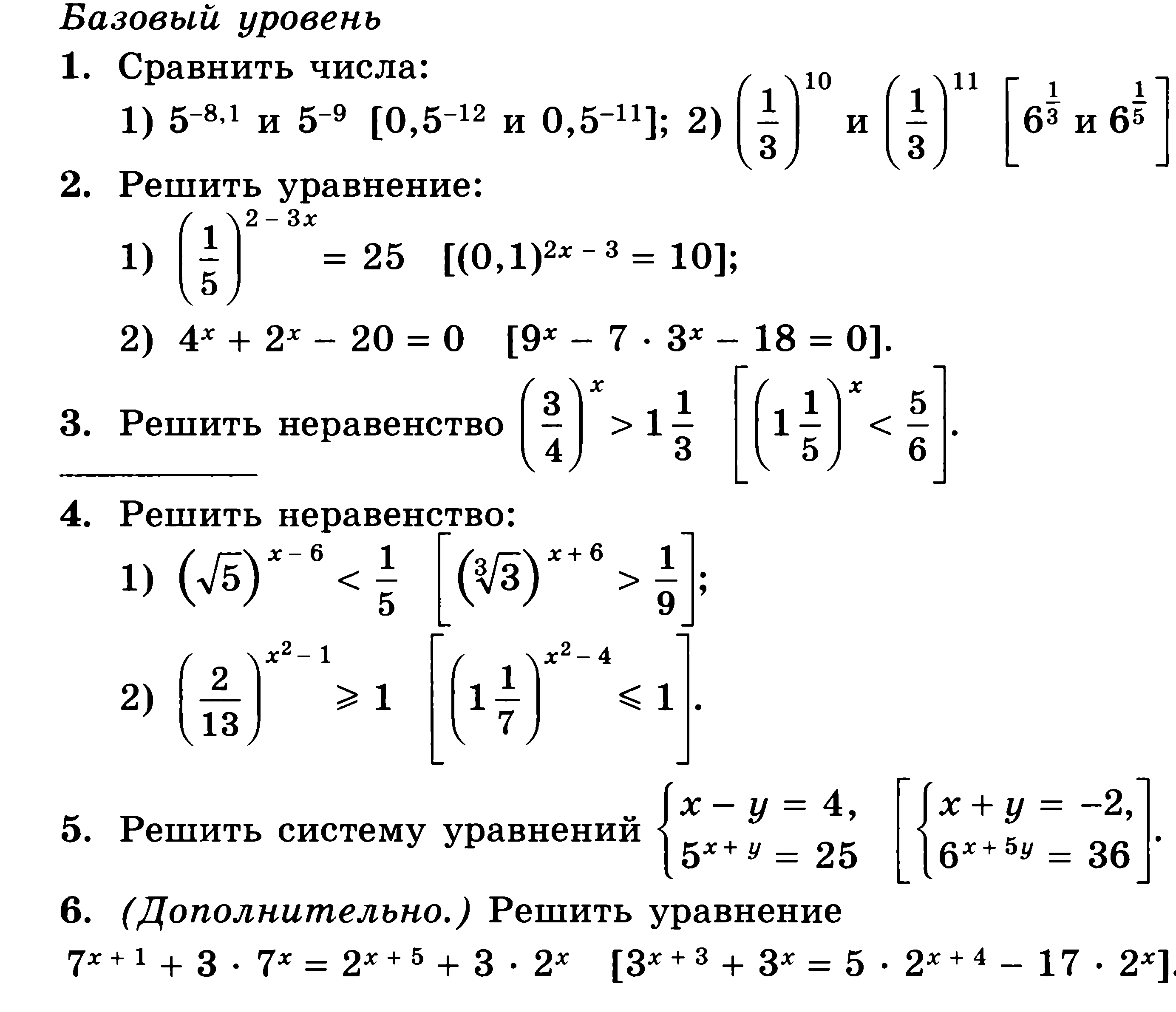

7.(Дополнительно) Решить неравенство
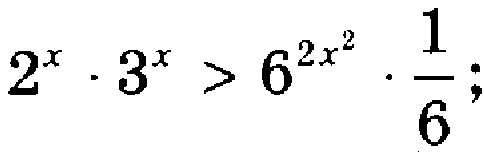
![]() [ ]
[ ]
![]()
Контрольная работа № 4 по теме «Логарифмическая функция»

Повышенный уровень
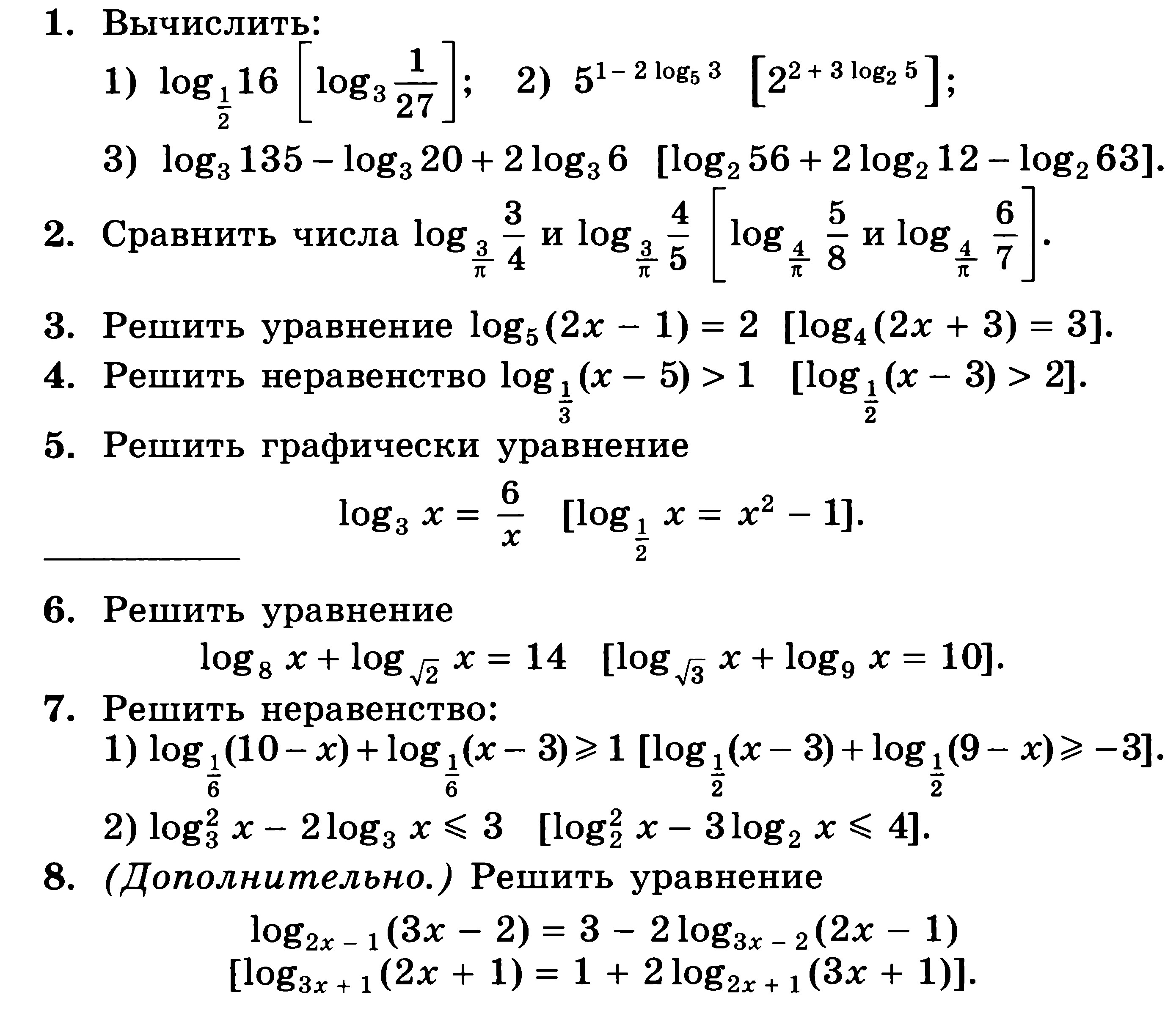
Контрольная работа № 5 по теме «Тригонометрические формулы»
 Повышенный уровень
Повышенный уровень
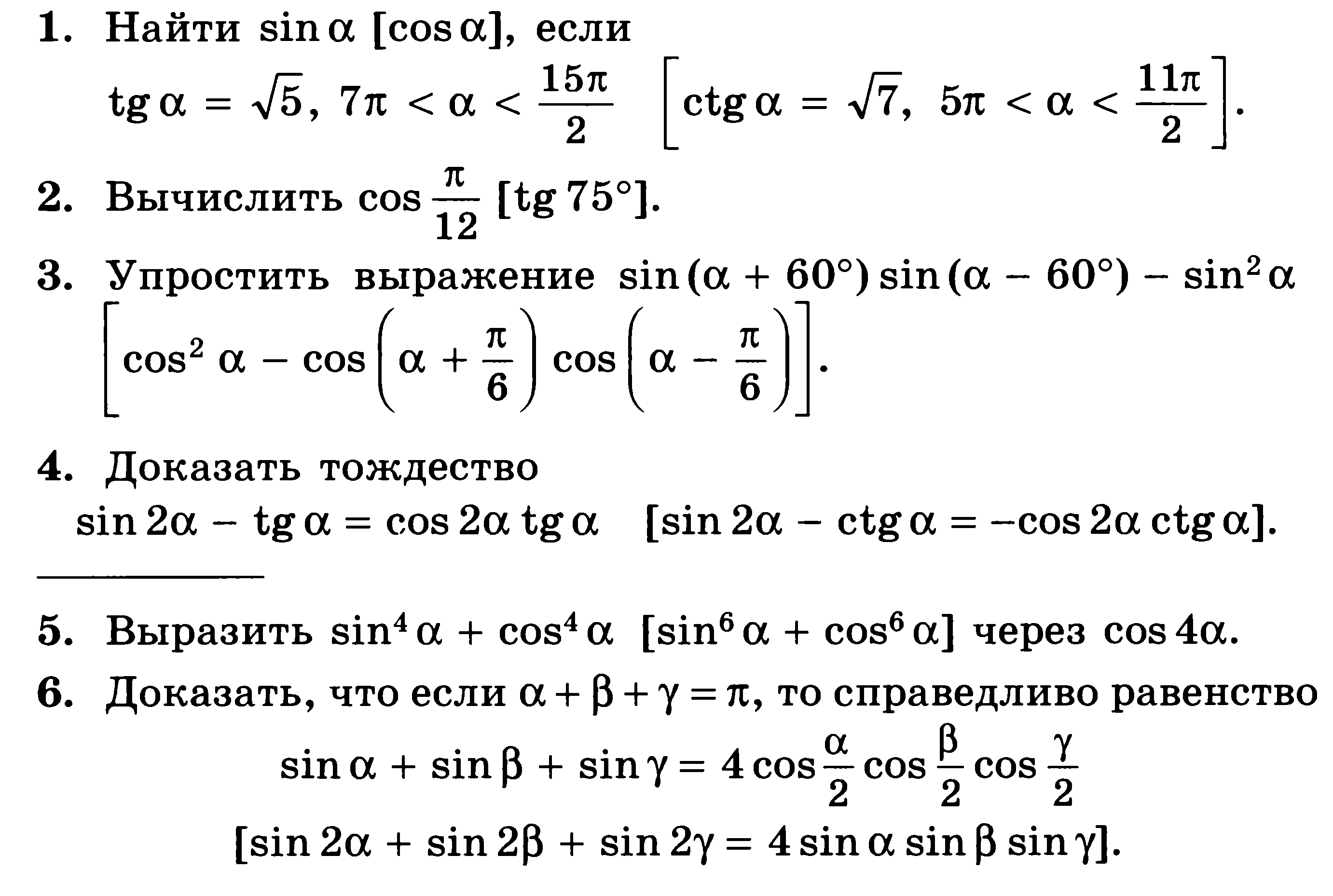
Контрольная работа № 6 по теме «Тригонометрические уравнения»
 Повышенный уровень
Повышенный уровень
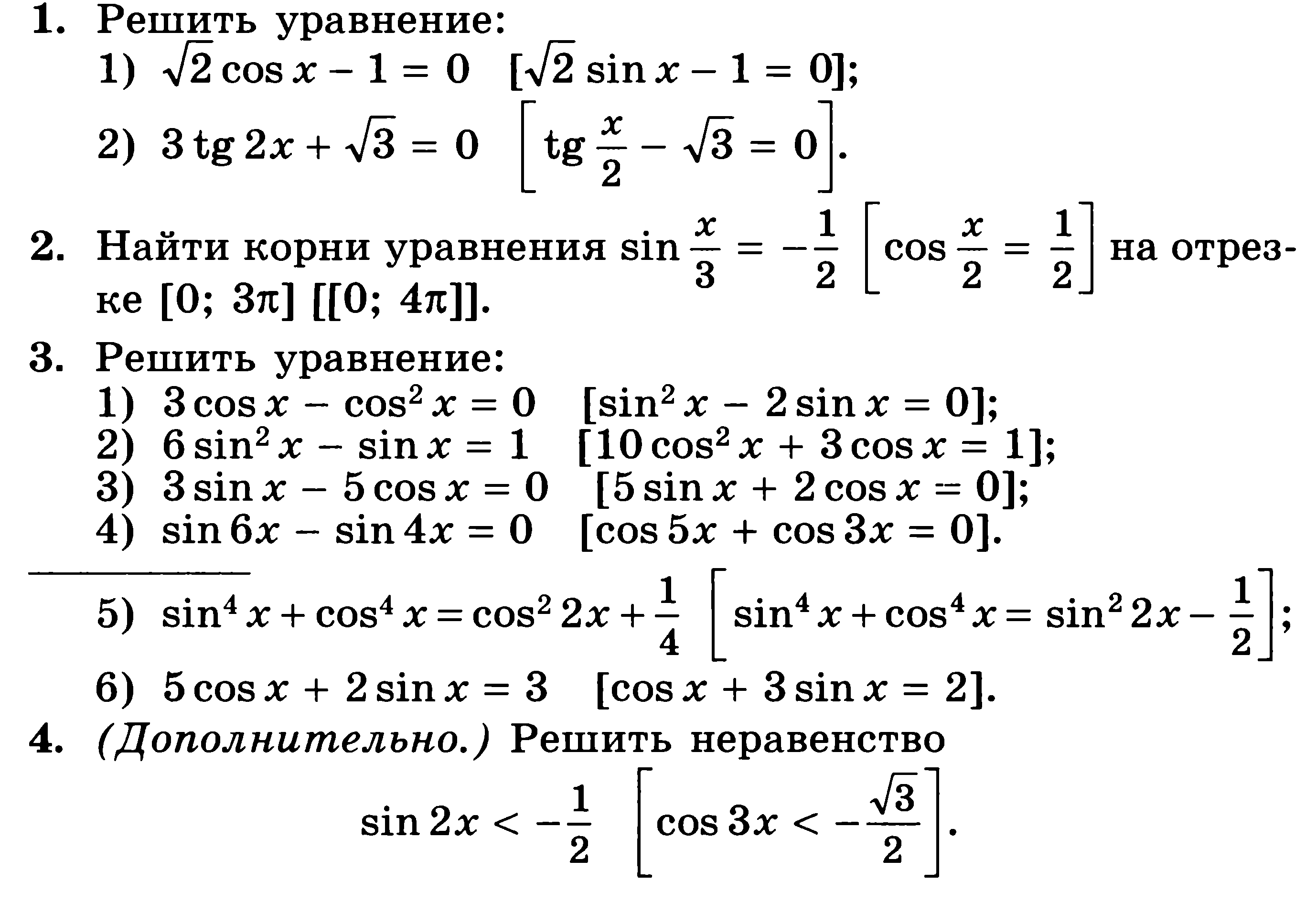
4

 Получите свидетельство
Получите свидетельство Вход
Вход











 Рабочая программа по алгебре 10 класс (1.01 MB)
Рабочая программа по алгебре 10 класс (1.01 MB)
 0
0 5108
5108 585
585 Нравится
2
Нравится
2




