Получите свидетельство
Вход
ПЗ №40 Координатный метод решения задач на многогранники
Дана пирамида с вершиной в точке D(Dx;Dy;Dz), основание которой – треугольник, построенный на векторах АВ и АС. Докажите, что ребро AD перпендикулярно основанию АВС. Найдите площадь боковой поверхности и объем пирамиды, если А(Ax;Ay;Az), B(Bx;By;Bz), C(Cx;Cy;Cz)
Координаты точек приведены в таблице. Номер варианта – номер по списку в журнале.
| N | Ax | Ay | Az | Bx | By | Bz | Cx | Cy | Cz | Dx | Dy | Dz |
| | 4 | 4 | 0 | 6 | 1 | 6 | 6 | 7 | -6 | 4 | 8 | 2 |
| | 3 | 4 | 1 | 5 | 3 | 2 | 5 | 5 | 0 | 3 | 7 | 4 |
| | 1 | 2 | 0 | 3 | -1 | 6 | 3 | 5 | -6 | 1 | 6 | 2 |
| | 2 | 3 | 0 | 4 | 2 | 1 | 4 | 4 | -1 | 2 | 6 | 3 |
| | 4 | 4 | -1 | 6 | 1 | 5 | 6 | 7 | -7 | 4 | 8 | 1 |
| | -1 | 0 | -3 | 1 | -1 | -2 | 1 | 1 | -4 | -1 | 3 | 0 |
| | 4 | -1 | 1 | 6 | -4 | 7 | 6 | 2 | -5 | 4 | 3 | 3 |
| | 2 | 4 | 0 | 4 | 3 | 1 | 4 | 5 | -1 | 2 | 7 | 3 |
| | 1 | 3 | -1 | 3 | 0 | 5 | 3 | 6 | -7 | 1 | 7 | 1 |
| | 3 | 5 | 1 | 5 | 4 | 2 | 5 | 6 | 0 | 3 | 7 | 3 |
| | -1 | 1 | -3 | 1 | -2 | 3 | 1 | 4 | -9 | -1 | 5 | -1 |
| | 2 | 5 | 0 | 4 | 4 | 1 | 4 | 6 | -1 | 2 | 7 | 2 |
| | 1 | 4 | -1 | 3 | 1 | 5 | 3 | 7 | -7 | 1 | 8 | 1 |
| | 3 | 6 | 1 | 5 | 5 | 2 | 5 | 7 | 0 | 3 | 8 | 3 |
| | -1 | 2 | -3 | 1 | -1 | 3 | 1 | 5 | -9 | -1 | 6 | -1 |
| | 1 | 2 | 2 | 3 | 1 | 3 | 3 | 3 | 1 | 1 | 4 | 4 |
| | 2 | 3 | 3 | 4 | 0 | 9 | 4 | 6 | -3 | 2 | 7 | 5 |
| | -2 | -1 | -1 | 0 | -5 | 3 | 0 | 3 | -5 | -2 | 5 | 5 |
| | 1 | 4 | 2 | 3 | 3 | 3 | 3 | 5 | 1 | 1 | 6 | 4 |
| | 2 | 5 | 3 | 4 | 2 | 9 | 4 | 8 | -3 | 2 | 9 | 5 |
| | -1 | 2 | 0 | 1 | -2 | 4 | 1 | 6 | -4 | -1 | 8 | 6 |
| | 3 | 8 | 0 | 5 | 7 | 1 | 5 | 9 | -1 | 3 | 10 | 2 |
| | 2 | 7 | -1 | 4 | 3 | 3 | 4 | 11 | -5 | 2 | 14 | 6 |
Пример. Дана пирамида с вершиной в точке
D(1;10;8), основание которой – треугольник, построенный на векторах АВ и АС. Докажите, что боковое ребро AD перпендикулярно плоскости основания АВС. Найдите площадь боковой поверхности и объем пирамиды, если А(1;2;0), B(3;-2;4), C(3;6;-4)
Решение. Выполним чертеж: D(1;10;8), А(1;2;0), B(3;-2;4), C(3;6;-4)
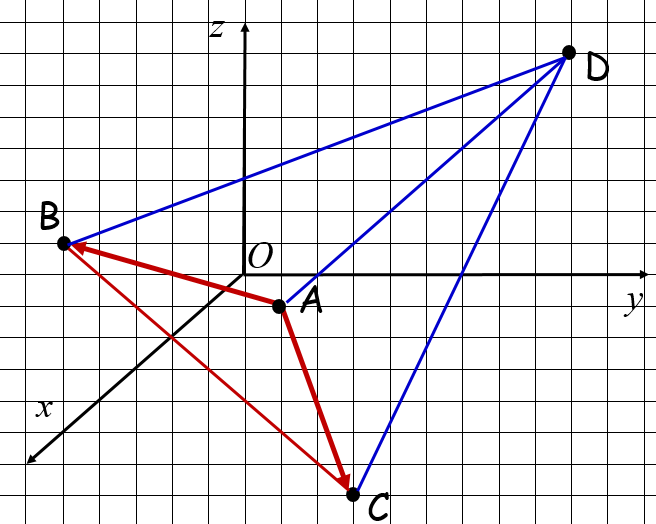
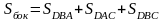. Найдем длины векторов 
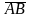и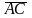 
. Зная координаты вектора, можно найти его длину, как корень квадратный из суммы квадратов его координат, т.е. если 
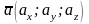, то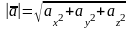 
.
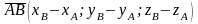
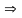
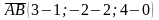
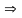
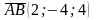, тогда 
.
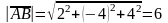Аналогично: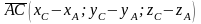 
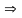
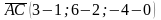
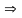
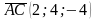, тогда 
.
, 
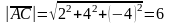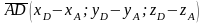
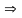
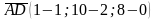
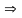
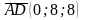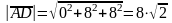
Если прямая АD перпендикулярна плоскости основания АВС, то вектор ФВ ортогонален и вектору АВ и вектору АС, а значит их скалярное произведение равно нулю.
.
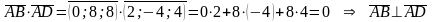
Т.о. действительно боковое ребро AD перпендикулярно АВС.
и 
, т.к. DA – общая, а угол между 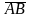и 
равен углу между 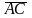и и равен 900.
Тогда .
Найдем площадь боковой грани DBA.
прямоугольный .
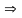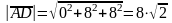. Значит, .
Рассмотрим 
. Для нахождения его площади воспользуемся формулой Герона:
, где
.
Слайд 45
,
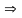
тогда .
,
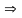
тогда .
,
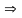
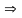
тогда .
Слайд 46
Итак, , 
, 
, 
, следовательно
.
Слайд 47
Итак , , , :
,
,
,
.
Окончательно, т.к. 
, и имеем:
.
Объем пирамиды равен одной трети произведения площади ее основания на высоту. Т.е. . Т.к. боковое ребро AD перпендикулярно плоскости основания АВС, то оно и является высотой пирамиды, т.е. . Значит объем призмы будем искать по формуле , или .
Найдем площадь основания АВС опять по формуле Герона:
, где
.
,
.
,
,
.
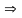
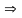
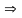
Итак , 
,
.
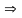
5
ПЗ №40 Координатный метод решения задач на многогранники (165.17 KB)
0
203
107
Нравится
0
