Пояснительная записка
Для жизни в современном обществе важным является формирование математического мышления, проявляющегося в определенных умственных навыках. В процессе математической деятельности в арсенал приемов и методов человеческого мышления естественным образом включается индукция и дедукция, обобщение и конкретизация, анализ и синтез, классификация и систематизация, абстрагирование и аналогия. Объекты математических умозаключений и правила их конструирования вскрывают механизм логических построений, вырабатывают умения формулировать, обосновывать и доказывать суждения, тем самым развивают логическое мышление.
Внеурочная деятельность является важной частью учебно - воспитательной работы в школе. Она способствует углублению знаний учащихся, развитию их дарований, логического мышления, расширяет кругозор. Кроме того, внеурочная деятельность по математике имеет большое воспитательное значение, ибо цель ее не только в том, чтобы осветить какой - либо узкий вопрос, но и в том, чтобы заинтересовать учащихся предметом, вовлечь их в серьезную самостоятельную работу.
Интеллектуальные игры для младних школьников – это самодеятельное объединение учащихся под руководством учителя, в рамках которого проводятся систематические занятия с учащимися во внеурочное время.
Внеурочные занятия по математике являются основной формой внеклассной работы с учащимися в начальных классах по подготовке к участию в олимпиадах по предмету. По целевым установкам и прогнозируемым результатам программа относится к образовательно - воспитательным.
Программа рассчитана на два года обучения. Образование осуществляется в виде теоретических и практических занятий для учащихся первого и второго года обучения – по 1 часу в неделю.
Оптимальная численность группы – 15 человек.
В основе внеурочной деятельности лежит принцип добровольности. Для обучения по программе принимаются все желающие учащиеся вторых классов.
Основная цель программы – развитие творческих способностей, логического мышления, углубление знаний, полученных на уроке, и расширение общего кругозора ребенка в процессе живого и забавного рассмотрения различных практических задач и вопросов, решаемых с помощью одной арифметики или первоначальных понятий об элементарной геометрии, изучения интересных фактов из истории математики.
Достижение этой цели обеспечено посредством решения следующих задач:
привитие интереса учащимся к математике;
углубление и расширение знаний учащихся по математике;
развитие математического кругозора, мышления, исследовательских умений учащихся;
формирование представлений о математике как части общечеловеческой культуры;
воспитание трудолюбия, терпения, настойчивости, инициативы.
Частично данные задачи реализуются и на уроке, но окончательная и полная реализация их переносится на внеклассные занятия.
Основными педагогическими принципами, обеспечивающими реализацию программы, являются:
учет возрастных и индивидуальных особенностей каждого ребенка;
доброжелательный психологический климат на занятиях;
личностно - деятельный подход к организации учебно - воспитательного процесса;
подбор методов занятий соответственно целям и содержанию занятий и эффективности их применения;
оптимальное сочетание форм деятельности;
преемственность, каждая новая тема логически связана с предыдущей;
доступность.
Программа может содержать разные уровни сложности изучаемого материала и позволяет найти оптимальный вариант работы с той или иной группой обучающихся. Данная программа является программой открытого типа, т. е. открыта для расширения, определенных изменений с учетом конкретных педагогических задач, запросов детей.
Ожидаемые результаты
По окончании обучения учащиеся должны знать:
нестандартные методы решения различных математических задач;
логические приемы, применяемые при решении задач;
историю развития математической науки, биографии известных ученых - математиков.
По окончании обучения учащиеся должны уметь:
рассуждать при решении логических задач, задач на смекалку, задач на эрудицию и интуицию;
систематизировать данные в виде таблиц при решении задач, при составлении математических кроссвордов, шарад и ребусов;
применять нестандартные методы при решении программных задач
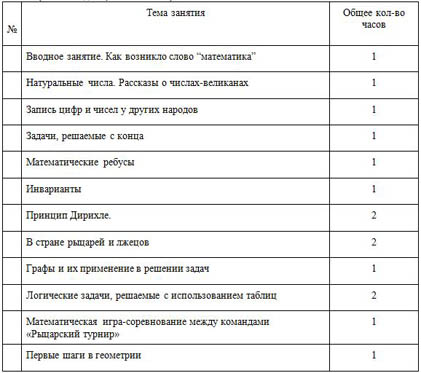
Учебно - тематический план 1 - го года занятий
Весь материал – смотрите документ.

 Получите свидетельство
Получите свидетельство Вход
Вход












 Программа внеурочной деятельности по решению нестандартных задач (32.83 КB)
Программа внеурочной деятельности по решению нестандартных задач (32.83 КB)
 0
0 1015
1015 142
142 Нравится
0
Нравится
0



