
Муниципальное общеобразовательное учреждение многопрофильная гимназия № 12 города Твери
| Согласовано Заместитель директора МОУ гимназии № 12
Шмитова Т.Г.
| Утверждено на заседании педагогического совета гимназии
Протокол № 1
от«30» августа 2012 г.
| Утверждаю Директор МОУ гимназии № 12 г. Твери
Т.В. Слесарева
Приказ № _______
от «___»_________2012 г.
|
РАБОЧАЯ ПРОГРАММА
элективного курса по математике
«Геометрия вокруг нас»
для 4-х классов
Содержание программы соответствует Федеральному государственному образовательному стандарту начального общего образования
Программа составлена учителем
первой квалификационной категории
МОУ гимназии № 12 г.Твери
Вахалиной Т. В.
Тверь
2012 год
Пояснительная записка
В основе построения данного курса лежит идея гуманизации математического образования, соответствующая современным представлениям о целях школьного образования и ставящая в центр внимания личность ученика, его интересы и способности. В основе методов и средств обучения лежит деятельностный подход. Курс позволяет обеспечить требуемый уровень подготовки школьников, предусматриваемый государственным стандартом математического образования, а также позволяет осуществлять при этом такую подготовку, которая является достаточной для углубленного изучения математики.
Начальный курс математики объединяет арифметический, алгебраический и геометрический материалы. При этом вопросы геометрии затрагиваются очень поверхностно, на них выделяется малое количество времени для изучения. Данный дополнительный курс ставит перед собой задачу формирования интереса к предмету геометрии, подготовку дальнейшего углубленного изучения геометрических понятий. Разрезание на части различных фигур, составление из полученных частей новых фигур помогают уяснить инвариантность площади и развить комбинаторные способности. Большое внимание при этом уделяется развитию речи и практических навыков черчения. Дети самостоятельно проверяют истинность высказываний, составляют различные построения из заданных фигур, выполняют действия по образцу, сравнивают, делают выводы.
Цель и задачи курса «Геометрия вокруг нас»
Цель: формирование всесторонне образованной и инициативной личности, владеющей системой математических знаний и умений, идейно-нравственных, культурных и этических принципов, норм поведения, которые
складываются в ходе учебно-воспитательного процесса и готовят её к активной деятельности и непрерывному образованию в современном обществе:
а) обучение деятельности - умению ставить цели, организовать свою деятельность, оценивать результаты своего труда,
б) формирование личностных качеств: ума, воли, чувств, эмоций, творческих способностей, познавательных мотивов деятельности,
в) формирование картины мира.
Задачи:
Обучающие:
ознакомление детей с основными геометрическими понятиями,
обеспечение прочного и сознательного овладения системой математических знаний и умений, необходимых для применения в практической деятельности, для изучения смежных дисциплин,
обеспечение интеллектуального развития, формирование качества мышления, характерные для математической деятельности и необходимые для полноценной жизни в обществе,
формирование умения следовать устным инструкциям, читать и зарисовывать схемы изделий,
обучение различным приемам работы с бумагой,
применение знаний, полученных на уроках окружающего мира, труда, рисования и других, для создания композиций с изделиями, выполненными в технике оригами.
Развивающие:
развитие внимания, памяти, логического и абстрактного мышления, пространственного воображения,
развитие мелкой моторики рук и глазомера,
выявление и развитие математических и творческих способностей.
Воспитательные:
воспитание интереса к предмету «Геометрия»,
расширение коммуникативных способностей детей,
формирование культуры труда и совершенствование трудовых навыков.
Особенности программы
Принципы:
Принципы, которые решают современные образовательные задачи с учётом запросов будущего:
1.Принцип деятельности включает ребёнка в учебно- познавательную деятельность. Самообучение называют деятельностным подходом.
2. Принцип целостного представления о мире в деятельностном подходе тесно связан с дидактическим принципом научности, но глубже по отношению к традиционной системе. Здесь речь идёт и о личностном отношении учащихся к полученным знаниям и умении применять их в своей практической деятельности.
3. Принцип непрерывности означает преемственность между всеми ступенями обучения на уровне методологии, содержания и методики.
4. Принцип минимакса заключается в следующем: учитель должен предложить ученику содержание образования по максимальному уровню, а ученик обязан усвоить это содержание по минимальному уровню.
5. Принцип психологической комфортности предполагает снятие по возможности всех стрессообразующих факторов учебного процесса, создание в классе и на уроке такой атмосферы, которая расковывает учеников, и, в которой они чувствуют себя уверенно.
6. Принцип вариативности предполагает развитие у детей вариативного мышления, т. е. понимания возможности различных вариантов решения задачи и умения осуществлять систематический перебор вариантов. Этот принцип снимает страх перед ошибкой, учит воспринимать неудачу не как трагедию, а как сигнал для её исправления.
7. Принцип творчества (креативности) предполагает максимальную ориентацию на творческое начало в учебной деятельности ученика, приобретение ими собственного опыта творческой деятельности.
8. Принцип системности. Развитие ребёнка - процесс, в котором взаимосвязаны и взаимозависимы все компоненты. Нельзя развивать лишь одну функцию. Необходима системная работа по развитию ребёнка.
9. Соответствие возрастным и индивидуальным особенностям.
10. Адекватность требований и нагрузок.
11. Постепенность.
12. Индивидуализация темпа работы.
13. Повторность материала.
Ценностными ориентирами содержания элективного курса являются:
– формирование умения рассуждать как компонента логической грамотности; освоение эвристических приемов рассуждений;
– формирование интеллектуальных умений, связанных с выбором стратегии решения, анализом ситуации, сопоставлением данных;
– развитие познавательной активности и самостоятельности учащихся;
– формирование способностей наблюдать, сравнивать, обобщать, находить
простейшие закономерности, использовать догадку, строить и проверять
простейшие гипотезы;
– формирование пространственных представлений и пространственного
воображения;
В работе используются следующие методы:
- словесные,
- наглядные,
- практические,
- исследовательские.
Для развития различных сторон мышления в программе предусмотрены разнообразные виды учебных действий, которые разбиты на три большие группы: репродуктивные, продуктивные ( творческие) и контролирующие.
К репродуктивным относятся:
а) исполнительские учебные действия, которые предполагают выполнение заданий по образцу,
б) воспроизводящие учебные действия направлены на формирование вычислительных и графических навыков.
Ко второй группе относятся три вида учебных действий - это обобщающие мыслительные действия, осуществляемые детьми под руководством учителя при объяснении нового материала в связи с выполнением заданий аналитического, сравнительного и обобщающего характера.
Поисковые учебные действия, при применении которых дети осуществляют отдельные шаги самостоятельного поиска новых знаний.
Преобразующие учебные действия, связанные с преобразованием примеров и задач и направленные на формирование диалектических умственных действий.
Контролирующие учебные действия направлены на формирование навыков самоконтроля.
Виды деятельности:
- творческие работы,
- задания на смекалку,
- логические задачи,
- упражнения на распознавание геометрических фигур,
- решение нестандартных задач,
- решение геометрических задач.
Место электива в учебном плане
Содержание электива отвечает требованию к организации внеурочной деятельности: соответствует курсу «Математика», не требует от учащихся дополнительных математических знаний. Тематика задач и заданий отражает реальные познавательные интересы детей, содержит полезную и любопытную информацию, интересные математические факты, способные дать простор воображению.
Занятия по этому курсу включают не только геометрический материал, но и задания конструкторско-практического задания, характера.
В методике проведения занятий учитываются возрастные особенности и возможности детей младшего школьного возраста, часть материала излагается в занимательной форме.
Целесообразно проводить элективный курс 1 раз в неделю учебного года.
Методы и приемы изучения геометрического материала
Одна из важных особенностей курса “Геометрия вокруг нас” - его геометрическая направленность, реализуемая в блоке практической геометрии и направленная на развитие и обогащение геометрических представлений детей и создание базы для развития графической грамотности, конструкторского мышления и конструкторских навыков.
Большое внимание в курсе уделяется поэтапному формированию навыков самостоятельного выполнения заданий, самостоятельному получению свойств геометрических понятий, самостоятельному решению некоторых важных проблемных вопросов, а также выполнению творческих заданий конструкторского плана.
В методике проведения занятий учитываются возрастные особенности детей младшего школьного возраста, и материал представляется в форме интересных заданий, дидактических игр и т.д.
Большое внимание в курсе уделяется развитию познавательных способностей. Термин познавательные способности понимается в курсе так, как его понимают в современной психологии, а именно: познавательные способности –это способности, которые включают в себя сенсорные способности (восприятие предметов и их внешних свойств) и интеллектуальные способности, обеспечивающие продуктивное овладение и оперирование знаниями, их знаковыми системами. Основа развития познавательных способностей детей как сенсорных, так и интеллектуальных - целенаправленное развитие при обучении математике познавательных процессов, среди которых в младшем школьном возрасте выделяются: внимание, воображение, память и мышление.
Общая характеристика элективного курса
Элективный курс «Геометрия вокруг нас» входит во внеурочную
деятельность по направлению общеинтеллектуальное развитие личности.
Программа предусматривает включение задач и заданий трудность которых определяется не столько математическим содержанием, сколько новизной и необычностью математической ситуации. Это способствует появлению желания отказаться от образца, проявить самостоятельность, формированию умений работать в условиях поиска, развитию сообразительности, любознательности.
В процессе выполнения заданий дети учатся видеть сходства и различия,
замечать изменения, выявлять причины и характер этих изменений, на этой основе формулировать выводы. Совместное с учителем движение от вопроса к ответу – это возможность научить ученика рассуждать, сомневаться, задумываться, стараться и самому найти выход – ответ.
Программа
4 класс (17 часов)
Высота. Медиана. Биссектриса.
Треугольники, высота, медиана, биссектриса основание и их построение. Прямоугольный треугольник. Катет и гипотенуза треугольника. Составление из треугольников других фигур.
«Новые» четырехугольники.
Параллелограмм. Ромб. Трапеция. Диагонали их и центр. Сходство этих фигур и различие.
Площадь.
Периметр и площадь. Сравнение. Нахождение площади с помощью палетки. Площадь треугольника. Площадь квадрата. Площадь прямоугольника. Нахождение площади нестандартных фигур с помощью палетки.
Геометрическая фигура.
Геометрическое тело.
Понятие объема. Геометрическое тело. Квадрат и куб. Сходство и различие. Построение пирамиды. Прямоугольник и параллелепипед. Построение параллелепипеда. Сходство и различие.
Круг, прямоугольник, цилиндр. Сходство и различие. Построение цилиндра. Знакомство с другими геометрическими фигурами.
Основные требования к знаниям, умениям и навыкам учащихся
1. Учащиеся должны знать термины: точка, прямая, отрезок, угол, ломаная, треугольник, прямоугольник, квадрат, длина, луч, четырехугольник, диагональ, сантиметр, а также название и назначение инструментов и приспособлений (линейка, треугольник).
2. Иметь представление и узнавать в фигурах и предметах окружающей среды простейшие геометрические фигуры: отрезок, угол, ломаную линию, прямоугольник, квадрат, треугольник.
3. Учащиеся должны уметь: измерить длину отрезка, определить, какой угол на глаз, различать фигуры, строить различные фигуры по заданию учителя.
4. Учащиеся должны владеть терминами, изученными во втором классе. Также учащиеся должны усвоить новые понятия такие как периметр, круг, окружность, овал, многоугольник, циркуль, транспортир, «центр», «радиус», «диаметр».
5. Иметь представление и узнавать в окружающих предметах фигуры, которые изучают в этом курсе.
6. Учащиеся должны уметь с помощью циркуля построить окружность, а также начертить радиус, провести диаметр, делить отрезок на несколько равных частей с помощью циркуля, делить угол пополам с помощью циркуля, знать и применять формулы периметра различных фигур, строить углы заданной величины с помощью транспортира и измерять данные, находить сумму углов треугольника, делить круг на (2, 4, 8), (3, 6, 12) равных частей с помощью циркуля.
7. Учащиеся должны владеть терминами: высота, медиана, биссектриса, основание, прямоугольный треугольник, катет, гипотенуза, параллелограмм, ромб, трапеция, куб, пирамида, параллелепипед, палетка, площадь, цилиндр. Учащиеся должны уметь: строить высоту, медиану, биссектрису треугольника, различные виды треугольников, параллелограмм, трапецию, а также проводить диагонали.
8. Строить ромб, находить центр.
9. Различать и находить сходство: (квадрат, куб, строить куб), (треугольник, параллелепипед, строить параллелепипед), (круг, прямоугольник и цилиндр, строить цилиндр).
Личностные, метапредметные и предметные результаты изучения
элективного курса «Геометрия вокруг нас»
Личностные результаты:
развитие любознательности, сообразительности при выполнении
разнообразных заданий проблемного и эвристического характера;
развитие внимательности, настойчивости, целеустремленности, умения
преодолевать трудности – качеств весьма важных в практической деятельности
любого человека;
воспитание чувства справедливости, ответственности;
развитие самостоятельности суждений, независимости и нестандартности
мышления.
Метапредметные результаты :
Выделять фигуру заданной формы на сложном чертеже.
Составлять фигуры из частей. Определять место заданной детали в конструкции.
Сопоставлять полученный (промежуточный, итоговый) результат с заданным условием.
Объяснять (доказывать) выбор деталей или способа действия при заданном условии.
Анализировать предложенные возможные варианты верного решения.
Моделировать объёмные фигуры из различных материалов (проволока, пластилин и др.) и из развёрток.
Осуществлять развернутые действия контроля и самоконтроля: сравнивать построенную конструкцию с образцом.
Предметные результаты:
таны, уголки, спички). Части фигуры. Место заданной фигуры в конструкции.
Разрезать и составлять фигуры. Делить заданные фигуры на равные по площади части.
Поиск заданных фигур в фигурах сложной конфигурации.
Решать задачи , формирующих геометрическую наблюдательность.
Распознавать (нахождение) окружности на орнаменте. Составлять
(вычерчивание) орнамента с использованием циркуля (по образцу, по собственному замыслу).
Объёмные фигуры: цилиндр, конус, пирамида, шар, куб. Моделировать из проволоки. Создавать объёмные фигуры из разверток: цилиндр, призма шестиугольная, призма треугольная, куб, конус, четырёхугольная пирамида, октаэдр, параллелепипед, усеченный конус, усеченная пирамида, пятиугольная пирамида, икосаэдр.
Универсальные учебные действия:
Сравнивать разные приемы действий, выбирать удобные способы для выполнения конкретного задания.
Моделировать в процессе совместного обсуждения алгоритм решения числового кроссворда; использовать его в ходе самостоятельной работы.
Применять изученные способы учебной работы и приёмы вычислений для работы с числовыми головоломками.
Анализировать правила игры. Действовать в соответствии с заданными правилами.
Включаться в групповую работу. Участвовать в обсуждении проблемных вопросов, высказывать собственное мнение и аргументировать его.
Выполнять пробное учебное действие, фиксировать индивидуальное затруднение в пробном действии.
Аргументировать свою позицию в коммуникации, учитывать разные мнения,
использовать критерии для обоснования своего суждения.
Сопоставлять полученный (промежуточный, итоговый) результат с заданным условием.
Контролировать свою деятельность: обнаруживать и исправлять ошибки.
4 класс (14 часов)
|
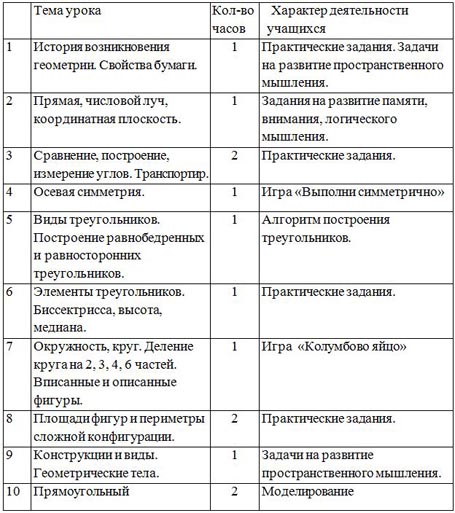
| Тема урока | Кол-во часов | Характер деятельности учащихся |
| 1 | История возникновения геометрии. Свойства бумаги. | 1 | Практические задания. Задачи на развитие пространственного мышления. |
| 2 | Прямая, числовой луч, координатная плоскость. | 1 | Задания на развитие памяти, внимания, логического мышления. |
| 3 | Сравнение, построение, измерение углов. Транспортир. | 2 | Практические задания. |
| 4 | Осевая симметрия. | 1 | Игра «Выполни симметрично» |
| 5 | Виды треугольников. Построение равнобедренных и равносторонних треугольников. | 1 | Алгоритм построения треугольников. |
| 6 | Элементы треугольников. Биссектрисса, высота, медиана. | 1 | Практические задания. |
| 7 | Окружность, круг. Деление круга на 2, 3, 4, 6 частей. Вписанные и описанные фигуры. | 1 | Игра «Колумбово яйцо» |
| 8 | Площади фигур и периметры сложной конфигурации. | 2 | Практические задания. |
| 9 | Конструкции и виды. Геометрические тела. | 1 | Задачи на развитие пространственного мышления. |
| 10 | Прямоугольный параллелепипед. Модель развёртки. | 2 | Моделирование параллелепипеда. Задание на сообразительность. |
| 11 | Цилиндр. | 1 | Задачи на развитие пространственного мышления. |
| 12 | Конус. Цилиндр. | 1 | Зрительный диктант. Загадки. Практическое задание. |
| 13 | Пирамида. Шар. | 1 | Графический диктант. Задание на развитие воображения. «Танграм». |
| 14 | Система старинных мер. Геометрический КВН. | 1 | Проверочные задания на сформированности геометрических понятий. |
| Всего 17 часов |
Оборудование и кадровое обеспечение программы
Для осуществления образовательного процесса по Программе «Геометрия вокруг нас» необходимы следующие принадлежности:
набор геометрических фигур;
компьютер, принтер, сканер, мультмедиапроектор;
Литература для учителя
В. Г. Житомирский, Л. Н. Шеврин «Путешествие по стране геометрии». М., « Педагогика-Пресс», 1994
Т.В. Жильцова, Л.А. Обухова «Поурочные разработки по наглядной геометрии», М., «ВАКО», 2004
Волина В. Праздник числа (Занимательная математика для детей): Книга для учителей и родителей. – М.: Знание, 1994. – 336 с.
Б.П. Никитин «Ступеньки творчества или развивающие игры», М., «Просвещение», 1990
Шадрина И.В. Методические рекомендации к комплекту рабочих тетрадей. 1-4 классы.- М. «Школьная Пресса». 2003
Шадрина И.В. Обучение математике в начальных классах. Пособие для учителей, родителей, студентов педвузов. – М. «Школьная Пресса». 2003
Шадрина И.В. Обучение геометрии в начальных классах. Пособие для учителей, родителей, студентов педвузов. – М. «Школьная Пресса». 2002
Литература для ученика
Волкова С.И., Пчёлкина О.Л. Математика и конструирование. Пособие для учащихся 4 класс.- М. «Просвещение», 2002
Шадрина И.В. Решаем геометрические задачи. 4 класс. Рабочая тетрадь. – М. «Школьная Пресса». 2003

 Получите свидетельство
Получите свидетельство Вход
Вход












 Программа элективного курса "Геометрия вокруг нас" (1.37 MB)
Программа элективного курса "Геометрия вокруг нас" (1.37 MB)
 0
0 776
776 53
53 Нравится
0
Нравится
0


