Получите свидетельство
Вход
Урок геометрии в 7г классе. учитель Кальницкий А. А. 14.12.2018
ПОВТОРЕНИЕ ПО ТЕМЕ: "ПРИЗНАКИ РАВЕНСТВА ТРЕУГОЛЬНИКОВ"
| Цель деятельности учителя | Создать условия для систематизации знаний, умений, навыков учащихся по данной теме; совершенствовать навыки решения задач по теме «Признаки равенства треугольников. Равнобедренный треугольник» | ||||
| Термины и понятия | Признаки равенства треугольников, боковая сторона, основание, медиана, биссектриса, высота, углы при основании | ||||
| Планируемые результаты | |||||
| Предметные умения | Универсальные учебные действия | ||||
| Применяют изученные понятия, результаты, методы для решения задач практического характера | Познавательные: умеют самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач. Регулятивные: умеют осуществлять контроль по результату и по способу действия на уровне произвольного внимания и вносить необходимые коррективы, контролировать процесс и результат учебной математической деятельности. Коммуникативные: умеют работать в сотрудничестве с учителем, находить общее решение и разрешать конфликты на основе согласования позиций и учета интересов. Личностные: осознают важность и необходимость изучения предмета | ||||
| Организация пространства | |||||
| Формы работы | Фронтальная (Ф); парная (П); индивидуальная (И) | ||||
| Образовательныересурсы | • Задания для фронтальной (парной) работы. • Тест | ||||
| I этап. Актуализация опорных знаний учащихся | |||||
| Цель деятельности | Совместная деятельность | ||||
| Устранить пробелы в знаниях учащихся | (Ф/И) Заслушать сочинения учащихся | ||||
| II этап. Тест | |||||
| Цель деятельности | Совместная деятельность | ||||
| Систематизировать теоретические знания учащихся | (И) Учащиеся выполняют тестовые задания (см. Ресурсный материал) | ||||
| III этап. Решение задач по готовым чертежам | |||||
| Цель деятельности | Совместная деятельность | ||||
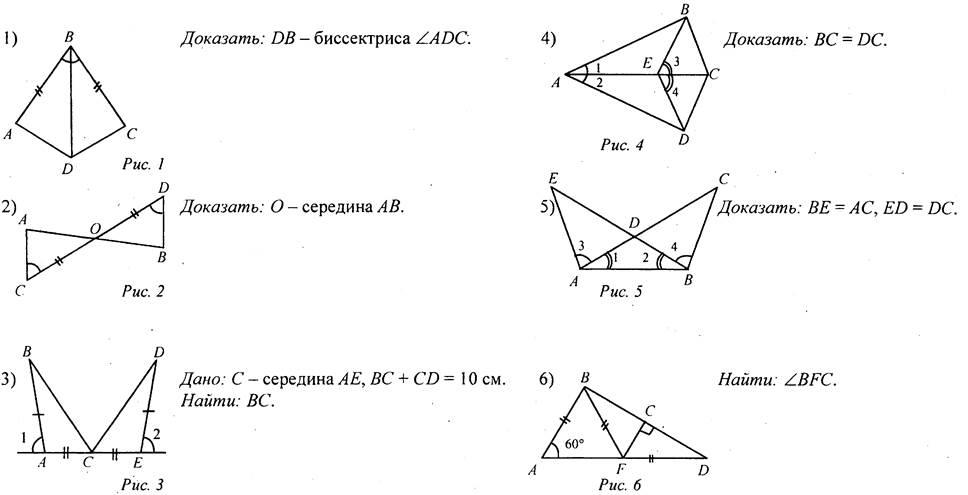
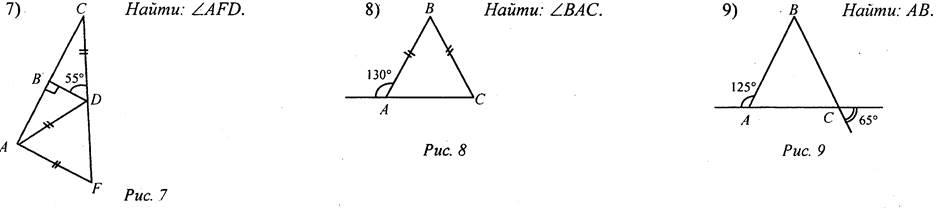
| Совершенствовать навыки решения задач | (Ф/И/П) Записать короткое решение к задачам по готовым чертежам.
| ||||
| IV этап. Итоги урока. Рефлексия | |||||
| Деятельность учителя | Деятельность учащихся | ||||
| - Уточните алгоритм исправления ошибок. - Назовите способы действий, вызвавшие затруднение. - Оцените собственную деятельность на уроке | (И) Домашнее задание: повторить главу III, вопросы 1-15; решить оставшиеся задачи. Дополнительные задачи: № 328-332 на выбор учащихся | ||||
|
|
|
|
|
| |
Ресурсный материал
Тест
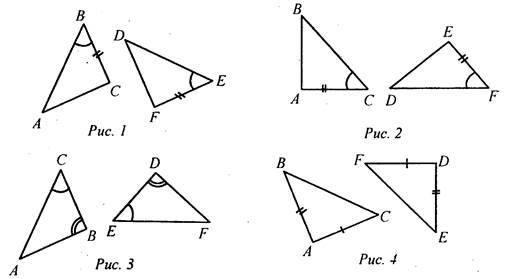
1. Для доказательства равенства ΔАВС и ΔDEF (рис. 1) достаточно доказать, что:
а) АВ = DF;
б) AC = DE;
в) АВ = DE.
2. Для доказательства равенства ΔАВС и ΔEDF (рис. 2) достаточно доказать, что:
a) ∠A = ∠D;
б) ∠B = ∠D;
в) ∠A = ∠E.
3. Из равенства ΔАВС и ΔFDE (рис. 3) следует, что:
a) AB = FD;
б) AC = DF;
в) АВ = EF.
4. Из равенства ΔАВС и ΔDEF (рис. 4) следует, что:
a) ∠B = ∠D;
б) ∠A = ∠E;
в) ∠C = ∠F.
5. В ΔАВС все стороны равны, и в ΔDEF все стороны равны. Чтобы доказать равенство ΔABC и ΔDEF, достаточно доказать, что:
a) ∠B = ∠D;
б) АВ = DE;
в) РАВС = РDEF.
6. «Медиана в равнобедренном треугольнике является биссектрисой и высотой». Это утверждение:
а) всегда верно;
б) всегда неверно;
в) может быть верно.
7. В каком треугольнике только одна его высота делит треугольник на два равных треугольника?
а) в любом;
б) равнобедренном;
в) равностороннем.
8. Если в треугольнике два угла равны, то этот треугольник:
а) равнобедренный;
б) равносторонний;
в) прямоугольный.
9. Если треугольник равносторонний, то:
а) он равнобедренный;
б) все его углы равны;
в) любая его биссектриса является его медианой и высотой.
Ответы: 1 - в; 2 - в; 3 - а; 4 - в; 5 - б, в; 6 - в; 7 - б; 8 - а; 9 - а, б, в.
Признаки равенства треугольников (81.12 KB)
0
353
13
Нравится
0
