1. Найти стационарные точки функции: y=x3-3x2+9
а) X1=3,x2=2;
b) X1=0, x2=2;
с) Х1= 5,х2=-1
2. Найти интервалы возрастания функции:
y= 2/3 х3-х2-4х
а) [-2;+∞]
b) (1/3;+∞)
c) [-1/3;+∞)
3. Найти интервалы убывания функции:
Y=2/x-3;
a) x>2 и х<2;
b) х>0;
c) х<3 и х >3.
4. Найти точки экстремума функции: y= 3x4-5x3
a) X=0 –max, x=5-min;
b) X=5/4- min;
c) Х= 5/4 – max;

5. Найти наибольшее и наименьшее значения функции
f(x)=x4-2x3+4 на отрезке[-2;1]
a) 36- наибольшее; 3- наименьшее;
b) 36-наименьшее; 3- наибольшее;
c) 0 – наибольшее; 3/2- наименьшее.
6. Найти наибольшее значение функции f(x)= x√1-х2 на интервале (0;1)
a) 4;
b) 1/2;
c) 2.
7. Найти вторую производную функции:
f(x) = x5-3x4+ 5x2-2
a) 20x3-36x2+10
b) 20x4-12x3+10x
c) 5x4-3x3+10x.
8. Найти точки перегиба функции: f(x) = x2lnx
a) x= e;
b) x=e- 3/2;
c) x=e2.
Весь материал - в документе.

 Получите свидетельство
Получите свидетельство Вход
Вход



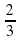 х3-х2-4х
х3-х2-4х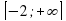
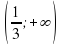
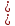 -
-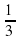 ;
;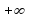 )
)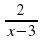 ;
;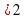 и х
и х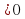 ;
;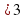 и х
и х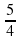 - min;
- min;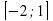
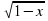 2 на интервале (0;1)
2 на интервале (0;1)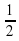 ;
;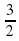 ;
;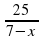 -
- 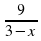 :
: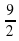 - min.
- min.








 Применение производной к исследованию функций (тест) (16.8 КB)
Применение производной к исследованию функций (тест) (16.8 КB)
 0
0 2151
2151 260
260 Нравится
0
Нравится
0


