Презентация "Выпуклые многоугольники"

ВЫПУКЛЫЕ МНОГОУГОЛЬНИКИ

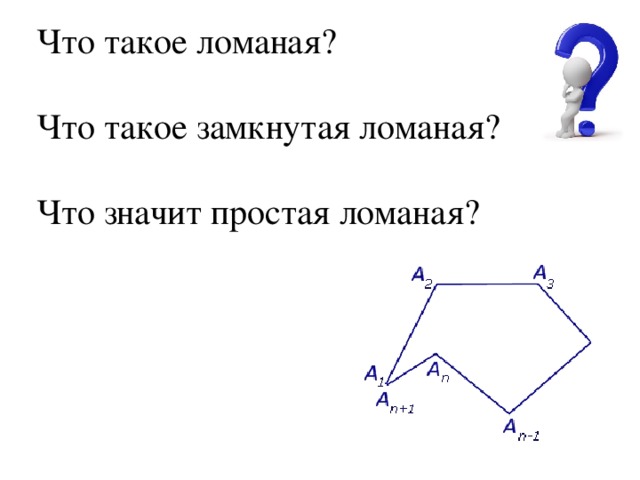
Что такое ломаная?

Что такое замкнутая ломаная?

Что значит простая ломаная?

МНОГОУГОЛЬНИК – простая замкнутая ломаная, соседние звенья которой не лежат на одной прямой.

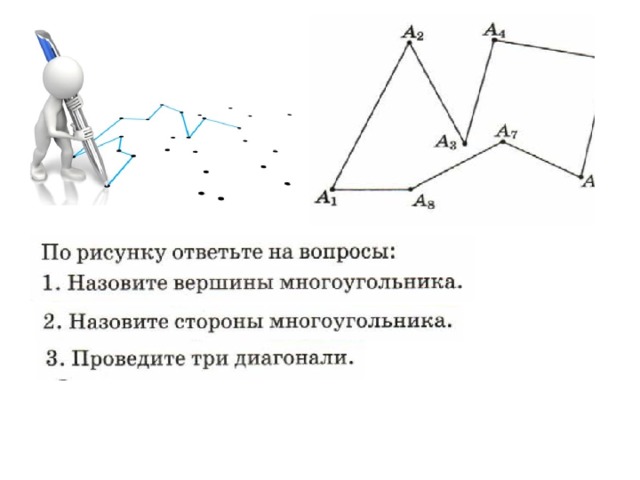
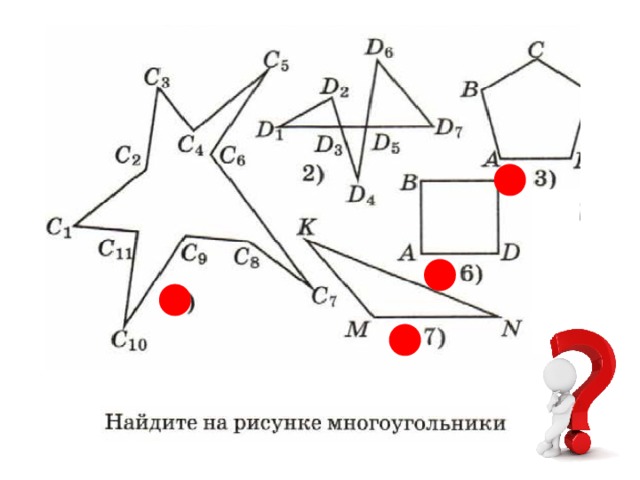
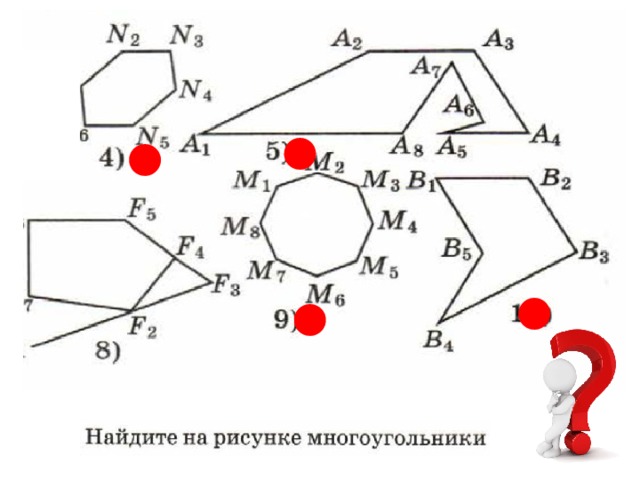
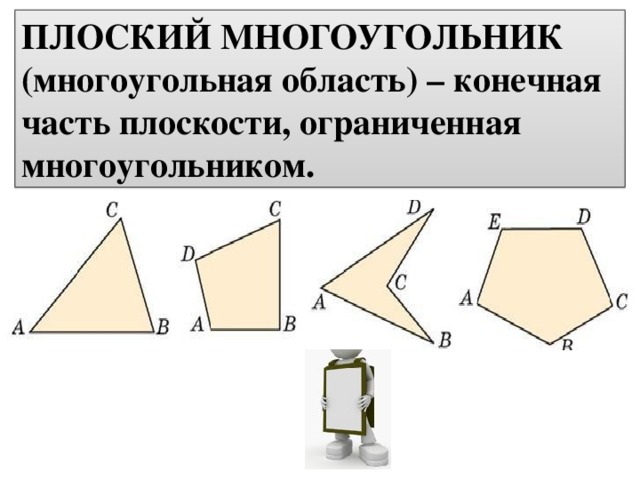
ПЛОСКИЙ МНОГОУГОЛЬНИК (многоугольная область) – конечная часть плоскости, ограниченная многоугольником.

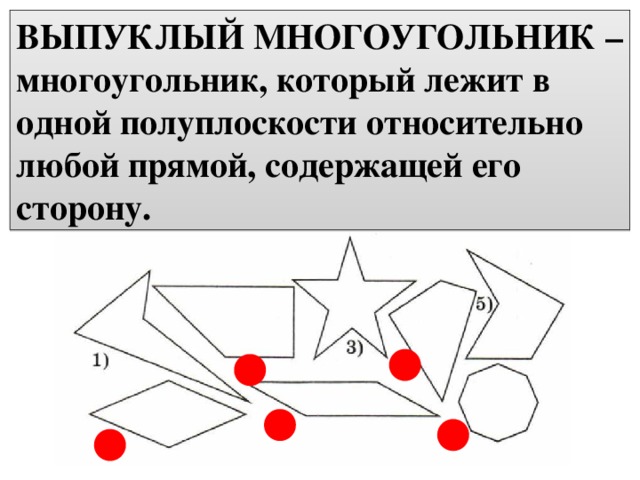
ВЫПУКЛЫЙ МНОГОУГОЛЬНИК – многоугольник, который лежит в одной полуплоскости относительно любой прямой, содержащей его сторону.

Приведите примеры известных четырехугольников, которые являются выпуклыми многоугольниками.

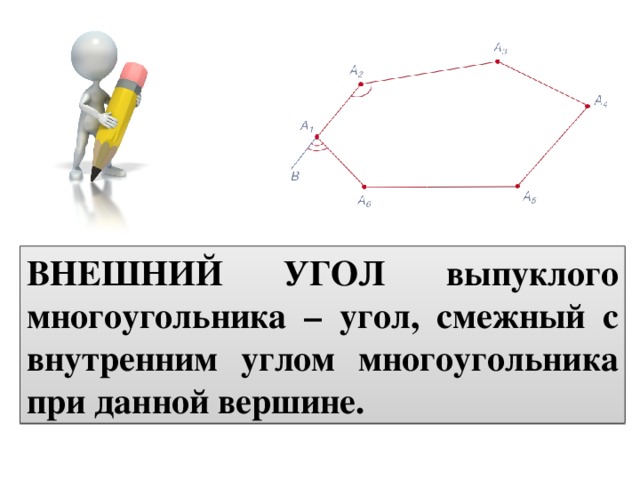
ВНЕШНИЙ УГОЛ выпуклого многоугольника – угол, смежный с внутренним углом многоугольника при данной вершине.

Теорема:

Сумма углов выпуклого

n-угольника равна 180°·(n – 2).

Вычислите сумму углов выпуклого

а) пятиугольника;

б) девятиугольника?

Сколько сторон имеет n-угольник, если сумма его внутренних углов равна:

а) 1260°;

б) 1980°?

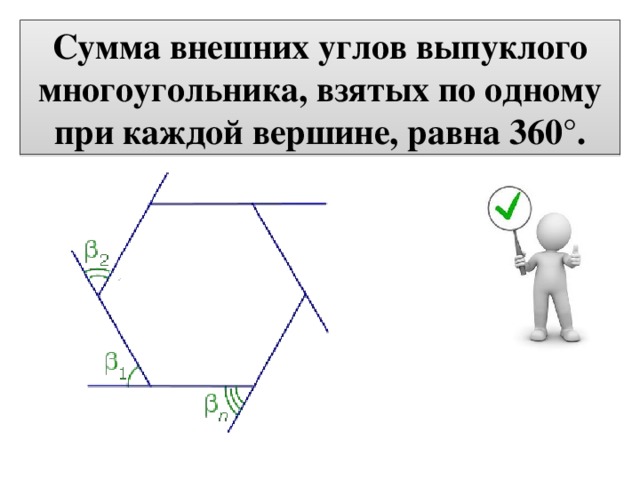
Сумма внешних углов выпуклого многоугольника, взятых по одному при каждой вершине, равна 360°.

Сумма углов выпуклого многоуголь-ника в два раза меньше суммы внешних углов, взятых по одному при каждой вершине. Найдите число сторон этого многоугольника.

Сколько сторон имеет выпуклый многоугольник, если все его внешние углы тупые?

Сколько сторон имеет выпуклый многоугольник, если сумма его внутренних углов с одним из внешних равна 2250°?

ДОМАШНЕЕ ЗАДАНИЕ

п. 115 №10

Повторить п.38-41