Презентация "Применение подобия треугольников"

Применение подобия треугольников

Учитель математики Кайнова Нина Ивановна

Наше настроение перед занятием…

Цель: рассмотреть различные способы нахождения расстояния до недоступной точки; научиться применять подобие треугольников для решения практических задач; показать взаимосвязь теории с практикой

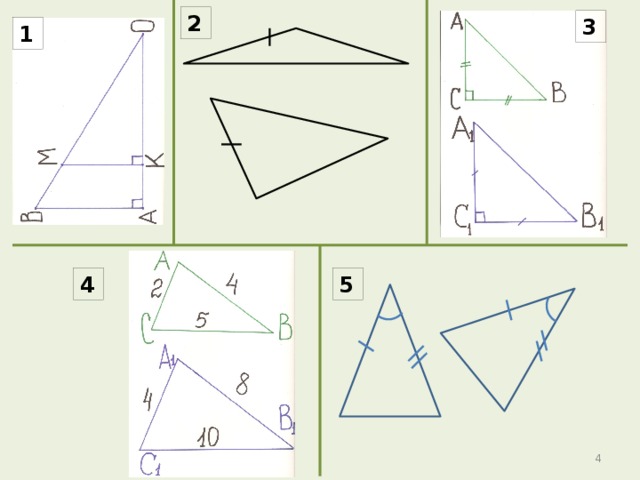
2

3

1

4

5

Задача № 582

Для определения расстояния от точки A до недоступной точки B на местности выбрали точку C и измерили отрезок AC, углы BAC и ACB. Затем построили на бумаге треугольник , подобный треугольнику ABC. Найдите AB, если AC = 42 м, = 6,3 см, = 7,2 см.

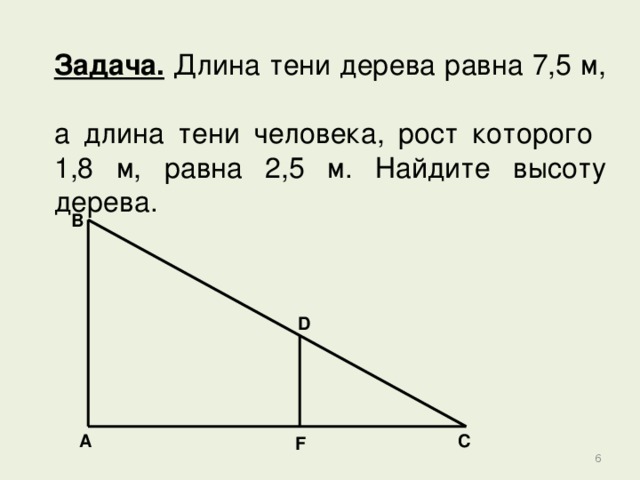
Задача. Длина тени дерева равна 7,5 м, а длина тени человека, рост которого 1,8 м, равна 2,5 м. Найдите высоту дерева.

B

D

A

C

F

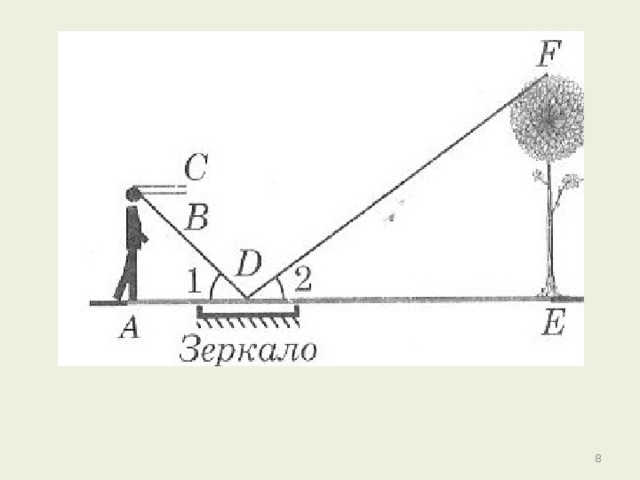
Лучи света в один момент времени падают под одним углом к поверхности Земли.

Каждый человек знает свой рост. Измеряем длину тени человека и длину тени дерева.

Используем подобие треугольников и вычисляем высоту дерева или другого объекта.

6

6

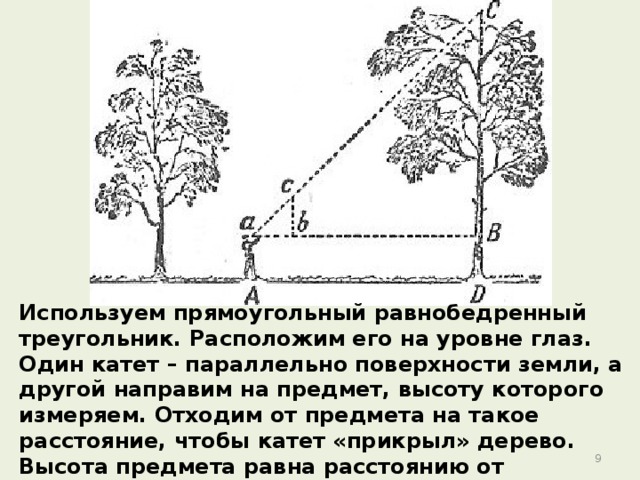
Используем прямоугольный равнобедренный треугольник. Расположим его на уровне глаз. Один катет – параллельно поверхности земли, а другой направим на предмет, высоту которого измеряем. Отходим от предмета на такое расстояние, чтобы катет «прикрыл» дерево. Высота предмета равна расстоянию от человека до основания предмета(прибавив рост человека).

6

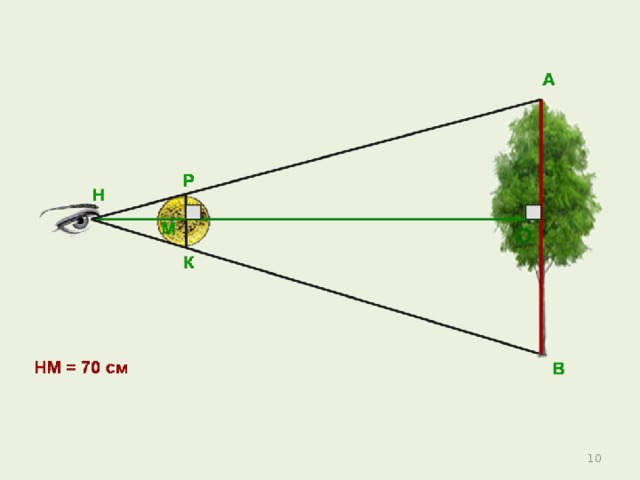
6

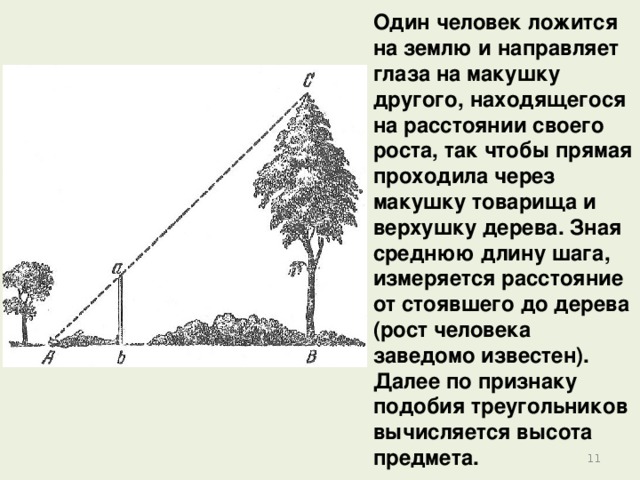
Один человек ложится на землю и направляет глаза на макушку другого, находящегося на расстоянии своего роста, так чтобы прямая проходила через макушку товарища и верхушку дерева. Зная среднюю длину шага, измеряется расстояние от стоявшего до дерева (рост человека заведомо известен). Далее по признаку подобия треугольников вычисляется высота предмета.

6

По способу

Жюля Верна (1828 – 1905)

12

Домашнее задание

К следующему занятию:

1) приготовить сообщение, каким способом Фалес измерил высоту пирамиды;

2) оформить свое сообщение в виде презентации (по желанию)

12

Наше настроение после занятия…

12