Практическое приложение подобия

Цели:

• Показать применение подобия в измерительных работах на местности;
• Совершенствовать навыки решения задач на применение теории подобных треугольников.
• Воспитание познавательной активности, культуры общения, привитие интереса к предмету;
• Развитие сознательного восприятия учебного материала.

Принадлежности: компьютер, экран, проектор, рисунки, магниты, прямоугольники 10х16,  ножницы, карточка ученика.

Ход урока.

1. Организационный момент.

Приветствие. Проверить готовность к уроку. Опрос дежурных об отсутствующих.

- тема нашего урока: практические приложения подобия. 

- цель урока: научиться применять теоретические знания о подобных треугольниках при решении задач.

- эпиграфом урока я выбрала слова Г.Галилея: «Природа формулирует свои законы языком математики».

2. Практические задания.

- Геометрия – это не просто наука о свойствах геометрических фигур. Геометрия – это целый мир, который окружает нас с самого рождения. Ведь всё, что мы видим вокруг, так или иначе относится к геометрии, ничто не ускользает от её внимательного взгляда. Геометрия помогает человеку идти по миру с широко открытыми глазами, учит внимательно смотреть вокруг и видеть красоту обычных вещей, смотреть и думать, думать и делать выводы.

- Постарайтесь сегодня на уроке следовать девизу

 «Смотри – думай – делай выводы», а выводы записывайте на карточку.

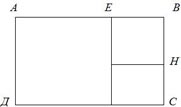
Задание 1.

Возьмите из бумаги прямоугольник со сторонами 10 см  и 16 см. Отрежьте от него квадрат наибольшей площади. Измерьте стороны получившегося прямоугольника. Запишите результат измерений на каждом прямоугольнике.

Затем с этим прямоугольником проделайте ту же операцию.

Найдём отношения сторон каждого из  этих трёх прямоугольников:

- в 1 прямоугольнике АВСД   АВ:ВС=16:10=1,6;

-в 2 прямоугольнике МЕВС  МЕ:ЕВ = 10:6=1,666…;

- в 3 прямоугольнике МФНС   МС:СН = 6:4 =1,5.

Вывод: так вот, ребята, прямоугольники, у которых стороны соотносятся приблизительно как 1,6 : 1, называют «Золотыми».

- Я предлагаю  вам посмотреть компьютерную презентацию.

(Просмотр)

- Математика всегда решала задачи, которые ставила перед ней жизнь, практика.

Послушайте историю о том, как однажды пришелец из далёкой Греции посрамил искусных египетских землемеров.

Случилось это в VI веке до новой эры, а пришельцем был Фалес из Милета.

( просмотреть ролик о Фалесе)

- В те времена греки не занимались геометрией, и Фалес решил познакомиться с египетской наукой. Египтяне задали ему трудную задачу: как найти высоту одной из громадных пирамид?

Фалес нашёл для этой задачи простое и красивое решение (а в математике очень часто простота – признак красоты).

Он воткнул длинную палку вертикально в землю и сказал: «Когда тень от этой палки будет той же длины, что и палка, тень от пирамиды будет иметь ту же длину, что и высота пирамиды»

Задание 2.

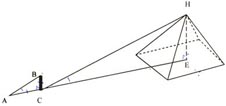
Фалес, вероятно, рассуждал так. Солнце от Земли очень далеко, поэтому идущие от него лучи можно без большой ошибки считать параллельными.

Попробуйте продолжить рассуждения ФАЛЕСА, используя рисунок. ВС – палка, СА – тень от палки, НЕ – высота пирамиды.

К доске желающий, остальные записывают свои рассуждения на карточку.

Задание 3.

- Так или нет рассуждал Фалес, сказать трудно. Но, вернувшись в родной город, он ещё раз удивил всех своим пониманием геометрии. Далеко от берега стоял на якоре корабль. Фалес сумел измерить расстояние от берега до корабля. В точности, как он это сделал, мы не знаем: его труды до нас не дошли. Подумайте и  предложите свой способ решения этой задачи, используя рисунки.

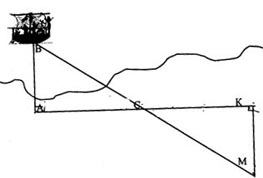
Решение.

     Пусть корабль находится в точке В, а наблюдатель в точке А. Построив в точке А прямой угол, необходимо отложить на берегу два равных отрезка АС=СК. В точке К вновь построить прямой угол, причём наблюдатель должен идти по перпендикуляру до тех пор, пока не дойдёт до точки М, из которой корабль В и точка С были бы видны лежащими на одной прямой. Прямоугольные треугольники АВС и СКМ равны, следовательно, АВ=КМ, а отрезок КМ можно непосредственно измерить.

Этот способ, получивший название метода триангуляции, нашёл применение в астрономии. С его помощью измерялись расстояния до небесных тел. Этот метод состоит из трёх этапов:

1. Выбираем на местности точку С, провешиваем отрезок АС и измеряем углы его. Затем с помощью астролябии измеряем углы  А=α  и С=β.
2. На листе бумаги строим треугольник А'В'С' с углами α и β при вершинах А'  и С' соответственно. Измеряем длины сторон А'В'  и А'С' этого треугольника.
3. Учитывая подобие треугольников АВС,  А'В'С'  и равенство АВ:А'В' = АС : А'С' , по известным длинам отрезков АС,  А'С' и А'В'  нетрудно найти длину отрезка АВ :    АВ=АС ∙ А'В' :  А'С'.

Задание 4 .

На  рисунке показано, как можно определить ширину ВК реки, рассматривая два подобных  треугольника  АВС  и  АМК.

Пояснить способ решения этой задачи на карточке.

Возможный план решения:

1. На местности выбрать точку А  и точку В₁  на берегу реки так, чтобы АВ₁ было перпендикулярно берегу.  В – точка на противоположном берегу.
2. На берегу реки выбрать точку  С, отличную от В₁.
3. Измерить углы  В₁АС  и АСВ.
4. На листе бумаги выполнить рисунок в некотором масштабе и провести прямую  В₁С₁ параллельно В₁В.
5. Вычислить АВ, а затем В₁В.

АВ : АС = АВ₁ : АС₁ =>АВ = АС ∙ АВ₁ : АС₁,  В₁В = АВ – АВ₁

Задание 5.

Однажды сын проходил с отцом по двору. Недавно прошёл дождь, и во дворе было много небольших луж. Посреди двора росло большое дерево. Сын спросил отца: «Чему равна высота этого дерева?» На этот вопрос отец ответил: «Давай не будем гадать, а измерим его высоту …   с помощью лужи. Я знаю свой рост – 180 см. Мне надо знать, ан какой высоте расположены глаза. Думаю, мы не сильно ошибёмся, если будем считать это расстояние равным 170 см. Мой шаг равен 90 см… А впрочем, это не важно. Сейчас я встану так, чтобы я мог видеть в этой луже отражение вершины дерева. Теперь подсчитаем, сколько шагов от меня до лужи. Получилось 3 шага. Так, а чему равно расстояние от лужи до дерева?.. 30 шагов. Значит, высота дерева равна…»

      Чему равна высота дерева? На карточке решите эту задачу.

Решение. 

Луч света ДС, отражаясь от лужи С, попадает  в глаз человеку В. По законам физики угол ДСЕ равен углу ВСЕ. Из подобия треугольников АВС и ЕДС выразим длину отрезка ДЕ:

ДЕ = ЕС ∙ АВ : АС = 30 ∙ 170 : 3 = 1700 см.

Ответ: 17 м.

Подведение итогов урока.  Оценки за урок.

Итак, чему сегодня вы научились на уроке?

- определять высоту предмета;

- определять расстояние до недоступной точки;

- определить ширину реки.

Я надеюсь, что эти знания вам пригодятся в жизни, а для того, чтобы вы закрепили их, запишите домашнее задание.

Сдайте карточки на проверку.

Домашнее задание.

П.64 измерительные работы на местности. №  579, № 581, № 583