Презентация по теме "Подобные слагаемые"

Слагаемые, имеющие одинаковую буквенную часть,

называются подобными слагаемыми.

Примеры:

2 x , - 3 x , 5 x - подобные слагаемые

4 ab , 12 ab , 36 ab - подобные слагаемые

Чтобы привести подобные слагаемые, надо сложить

их коэффициенты и полученный результат умножить

на общую буквенную часть.

В этом примере все слагаемые подобные,

у них одинаковая буквенная часть.

Выполняем действия с коэффициентами и результат

умножаем на буквенную часть.

У коэффициента тот знак, который перед ним стоит.

Пример:

образец оформления задания.

3 a – 6 a +2 a = (3 – 6 +2)∙ a =-1 ∙ a = - a

Бывает, что в выражении присутствует ни одна группа подобных слагаемых.

1)Подчеркиваем первую группу подобных слагаемых одной чертой,

вторую группу подобных слагаемых – двумя чертами,

третью группу подобных слагаемых – двумя пунктирными чертами.

2)Начинаем выполнять действия с коэффициентами

в каждой группе подобных слагаемых.

3)Полученные результаты умножаем на буквенную часть в каждой группе.

Помним, что у коэффициента тот знак, который перед ним стоит.

Пример: ( образец оформления задания )

5 a + 6a + 7b – 2 – 3b – 3a – 6 = (5 + 6 -3 )∙ a + (7 – 3) ∙b + (-2 -6) = 8a + 4 b - 8

Часто в выражении прежде, чем привести подобные слагаемые,

нужно сначала раскрыть скобки.

Правила раскрытия скобок:

 Если перед скобками стоит знак + , то можно опустить скобки и

этот знак + , сохранив знаки слагаемых, стоящих в скобках.

 Если перед скобками стоит знак - , нужно эти скобки опустить,

а знаки у слагаемых, стоящих в скобках поменять на противоположные .

 Применение распределительного закона умножения

a ∙ ( b +c) = a ∙ c + b ∙ c a ∙ ( b −c) = a ∙ c − b ∙ c

Примеры: ( образец оформления задания )

(

− 2 ∙ (5 − 3 y ) + 4 ∙ (3 − 2 y ) = −2∙ 5 −2 ∙ (−3 y ) + 4∙ 3 +

+4∙ (−2 y ) = −10 + 6 y +12 − 8 y = (−10 + 12) + (6 −8)∙ y=

= 2 – 2 y

2

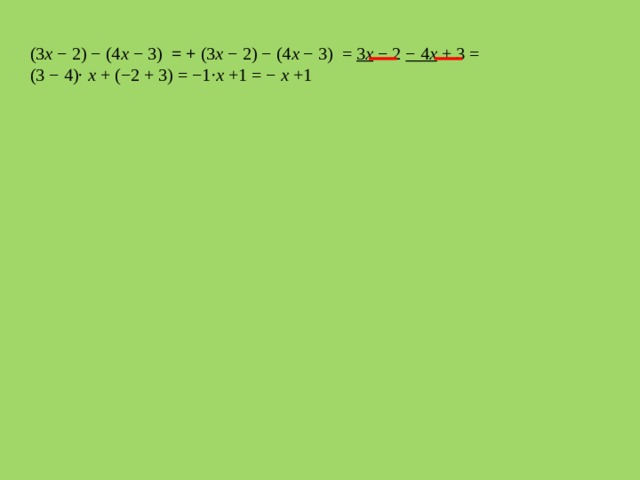
(3 x − 2) − (4 x − 3) = + (3 x − 2) − (4 x − 3) = 3 x − 2 − 4 x + 3 =

(3 − 4)∙ x + (−2 + 3) = −1∙ x +1 = − x +1