Презентация по теме "Логарифмы"

• Логарифмы. Решение логарифмических уравнений.

Логарифмы. Решение логарифмических уравнений и неравенств.

Презентацию подготовил: Маслюкова С.В.,

преподаватель ГАПОУ РС(Я) «МРТК»

филиал «Айхальский»

Понятие логарифма

При любом и степень с произвольным действительным показателем определена и равна некоторому положительному действительному числу : Показатель 𝑝 степени называется логарифмом этой степени с основанием .

Понятие логарифма.

Логарифмом положительного числа по положительному и не равному основанию : называется показатель степени, при возведении в который числа получается .

или

,

тогда

Определение логарифма.

Десятичный логарифм и натуральный логарифм

Десятичным логарифмом называется логарифм, если его основание равно 10 .

Обозначение десятичного логарифма: .

Натуральным логарифмом называется логарифм, если его основание равно числу .

Обозначение натурального логарифма: .

• Методы решения логарифмических уравнений
• 1. Метод потенцирования.
• 2. Функционально-графический метод.
• 3. Метод разложения на множители.
• 4. Метод замены переменной.
• 5. Метод логарифмирования.
• 6.По определению логарифма
• 7.Приведение к одному основанию

Методы решения простейших логарифмических уравнений.

• Решение простейших логарифмических уравнений
• № 1. Метод логарифмирования
• Решите уравнение .
• Решение.
• ; ; ; ; .
• Ответ. .

• № 2. Метод потенцирования
• Решите уравнение .
• Решение.
• ; ; ; .
• Ответ. .

Решение простейших логарифмических уравнений.

№ 3 . Метод замены переменной

Решите уравнение .

Решение.

Область определения уравнения:

.

Преобразуем данное уравнение:

.

Решаем методом замены переменной.

Пусть , тогда уравнение принимает вид:

.

Учитывая, что , получаем уравнение

Обратная замена:

Ответ.

№ 4. Метод разложения на множители

Решите уравнение .

Решение.

Находим область определения уравнения:

.

Преобразовываем данное уравнение

Учитывая область определения уравнения, получаем .

Ответ. .

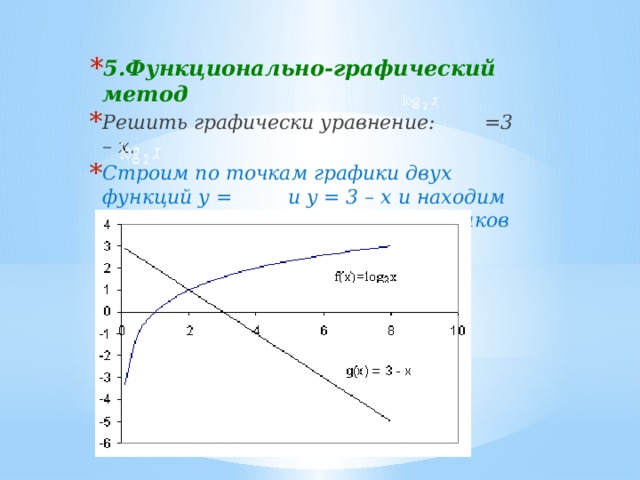
• 5.Функционально-графический метод
• Решить графически уравнение: =3 – x.
• Строим по точкам графики двух функций у = и y = 3 – x и находим абсциссу точек пересечения графиков

0, прологарифмируем обе части уравнения по основанию 10: Применим свойство логарифма степени: (lgx + 3) lgx = lg 10000 (lgx + 3) lgx = 4 Пусть lgx = y, тогда (у + 3)у = 4 , (D 0) корни по теореме Виета: у1 = -4 и у2 = 1. Вернемся к замене, получим: lgx = -4, ; lgx = 1, . Ответ: 0,0001; 10. " width="640"

• 6. Логарифмирование обеих частей уравнения
• Решить уравнение:
• Решение: ОДЗ: х0, прологарифмируем обе части уравнения по основанию 10:
• Применим свойство логарифма степени:
• (lgx + 3) lgx = lg 10000
• (lgx + 3) lgx = 4
• Пусть lgx = y, тогда (у + 3)у = 4
• , (D 0) корни по теореме Виета: у1 = -4 и у2 = 1.
• Вернемся к замене, получим: lgx = -4, ; lgx = 1, .
• Ответ: 0,0001; 10.

0. Перейдем к основанию 3. Ответ : 9. " width="640"

• 7. Приведение к одному основанию

Решите уравнение:

Решение: ОДЗ: х0. Перейдем к основанию 3.

Ответ : 9.

Свойства логарифмов

• 1 ) Если то

• 2) Если то

3)

4)

5)

6)

7 )

8)

9) ;

Свойства логарифмов.

10) , ;

11) , ;

12) , если ;

13) , если –чётное число,

, если –нечётное число.

Свойства логарифмов.

• Примеры с логарифмами
• Найдите значение выражения:
• № 1. ;
• № 2. ;
• № 3. ;
• № 1. ;
• № 2. ;
• № 3. ;
• № 1. ;
• № 2. ;
• № 3. ;

Примеры с логарифмами.

• № 1. ;
• № 2. ;
• № 3. ;
• № 1. ;
• № 2. ;
• № 3. ;
• № 1. ;
• № 2. ;
• № 3. ;
• № 1. ;
• № 2. ;

Примеры с логарифмами.

• № 3. ;
• № 1. ;
• № 2. ;
• № 3.

Примеры с логарифмами.

• Решение примеров с логарифмами
• № 1. .
• Ответ. .
• № 2. .
• Ответ. .
• № 3. .
• Ответ. .
• № 1. .
• Ответ. .
• № 2.
• .
• Ответ. .

Решение примеров с логарифмами.

Решение примеров с логарифмами.

• № 2. .
• Ответ. .
• № 3. .
• Ответ.
• № 1. .
• Ответ. .
• № 2.
• .
• Ответ.

Решение примеров с логарифмами.

• № 3. .
• Ответ.
• № 1. .
• Ответ. .
• № 2. .
• Ответ. .
• № 3 . .
• Ответ. .
• № 1. .
• Ответ. .

Решение примеров с логарифмами.

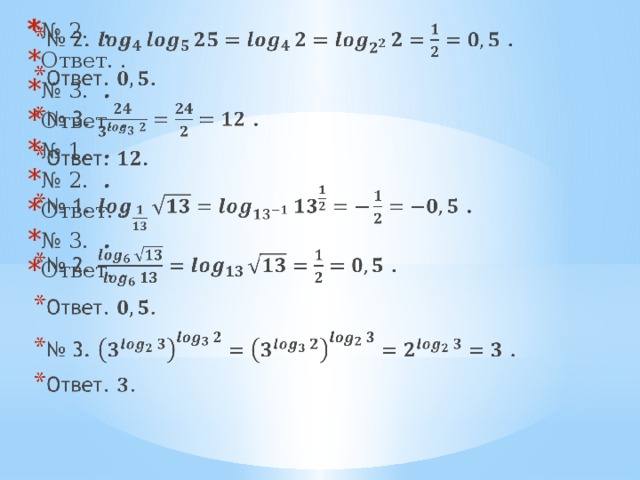
• № 2. .
• Ответ. .
• № 3. .
• Ответ. .
• № 1. .
• № 2. .
• Ответ. .
• № 3. .
• Ответ. .

Решение примеров с логарифмами.

№ 1 Решите уравнение .

• Решение.
• .
• Ответ. .

Решение простейших логарифмических уравнений.

• № 2 Решите уравнение .
• Решение.
• .

• Ответ. .

Решение простейших логарифмических уравнений.

• № 3 Решите уравнение .
• Решение.
• Преобразуем данное уравнение, воспользовавшись свойствами логарифма. Данное уравнение равносильно системе:

Решение логарифмических уравнений.

• Решим первое уравнение системы:
• .
• Учитывая, что и , получаем .
• Ответ. .

Решение логарифмических уравнений.

• Домашнее задание:
• 1.Повторить свойства логарифмов.
• 2.Повторить методы решения логарифмических уравнений.
• 3.Решить логарифмические уравнения.

• СПАСИБО
• ЗА ВНИМАНИЕ!