Презентация по теме "Линейные уравнения с одной переменной"

Линейные уравнения с одной переменной

Выполнила Саранина Р.В.

Равенство,содержащее переменную-называются уравнением с одной переменной. Корнем уравнения называется значение переменной,при котором уравнение обращается в верное равенство. Решить уравнение-значит найти его корни или доказать,что корней нет

Уравнение вида a x= b ,где х-переменная, а и b некоторые числа,называется линейным уравнением.

1. ax=b , x=b/a ,при а≠0имеет один корень. 2. ax=b ,при а=0,не имеет корней. 3. ах=b ,при а=0,b=0 любое значение х является корнем уравнения.

Сколько корней имеют уравнения:

2х=4 6х=0

5х-5х=5 5х-5х=0

0,5х-3=3 3х+4=4

Является ли корнем уравнения х(х-5)=6 число: а)1, б)-1, в)6, г)-6

Алгоритм решения линейных уравнений с одной переменной : 1.Раскрыть скобки. 2.Собрать члены,содержащие переменные,в одной части уравнения,остальные в другой. 3.Привести подобные слагаемые в обеих частях уравнения. 4.Разделить обе части уравнения на коэффициент при неизвестном.

Свойства,которые используют при решении уравнений : - если в уравнении перенести слагаемые из одной части в другую,изменив его знак,то получим уравнение,равносильное данному; -если обе части уравнения умножить или разделитьна одно и то же отличное от нуля число,то получится уравнение ,равносильное данному.

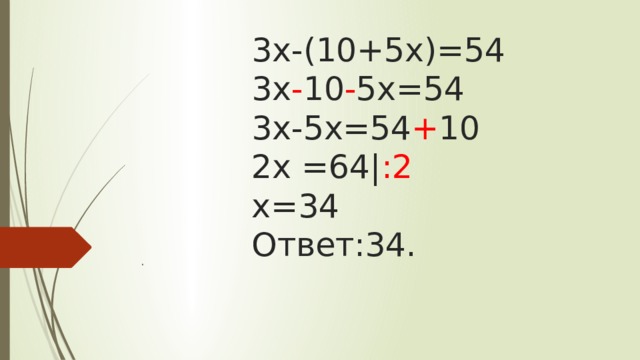
3х-(10+5х)=54 3х - 10 - 5х=54 3х-5х=54 + 10 2х =64| :2 х=34 Ответ:34.

.