Презентация по теме "Конус"

Конус. Площадь поверхности конуса

МБОУ «СОШ №27 им.Т.А.Абатаева»

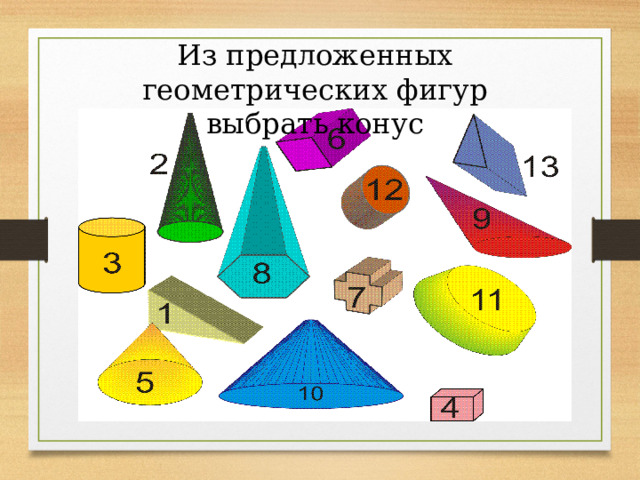
Из предложенных геометрических фигур выбрать конус

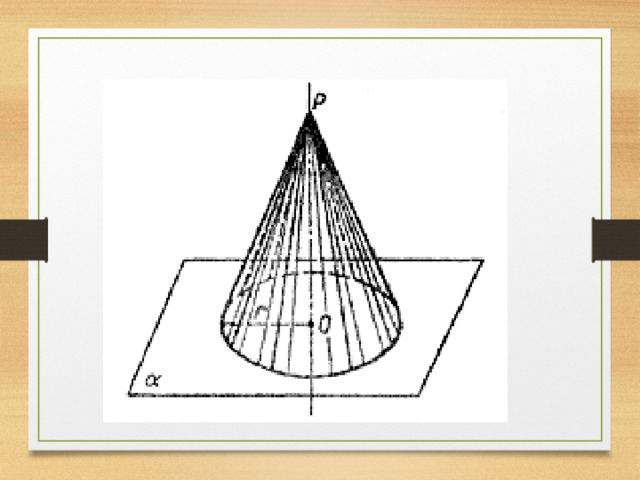
Коническая поверхность

Коническая поверхность

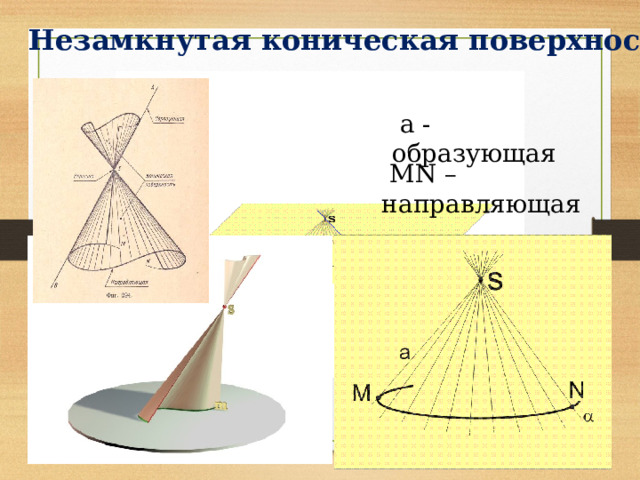
Незамкнутая коническая поверхность

а - образующая

MN – направляющая

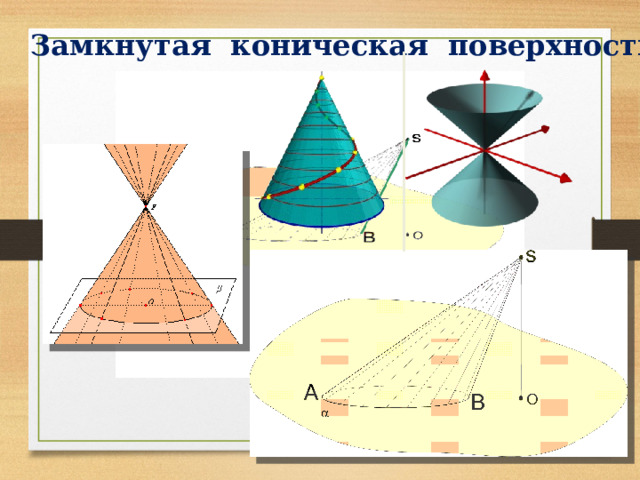
Замкнутая коническая поверхность

Коническая поверхность - поверхность, образованная движением прямой, которая проходит через данную точку и пересекает данную плоскую линию.

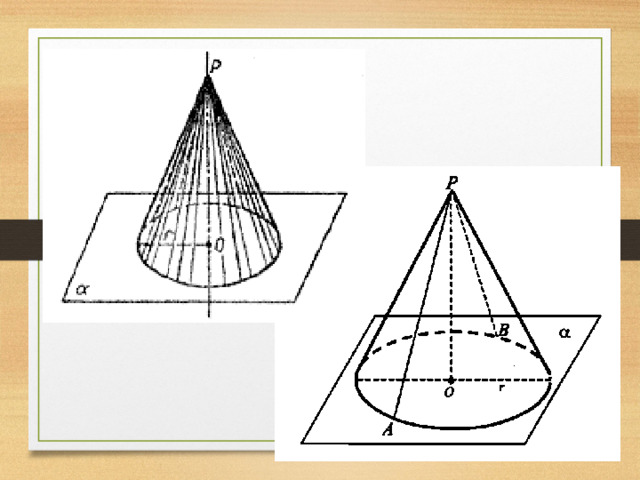
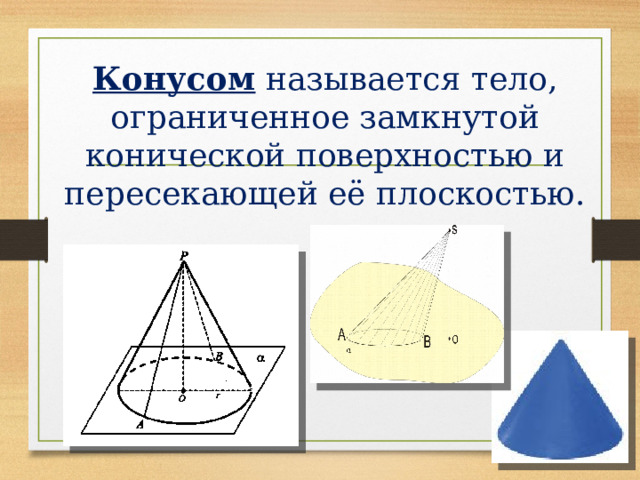
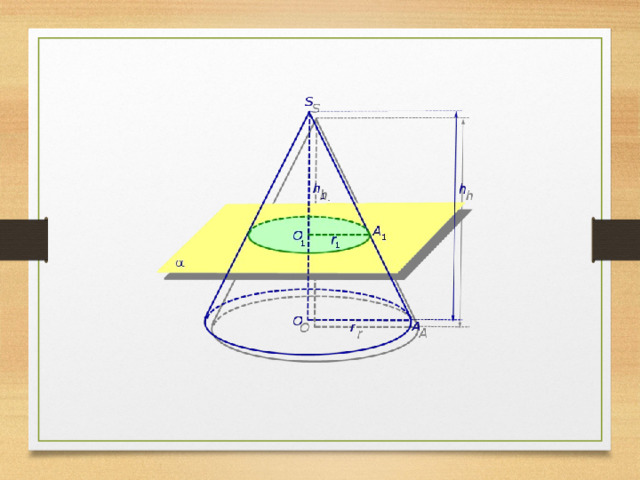
Конусом называется тело, ограниченное замкнутой конической поверхностью и пересекающей её плоскостью.

Конус

SO  (SO=Н, SO=h)

SO-высота конуса

SA-образующая

S-вершина конуса

Кривая ABA- направляющая.

Пусть прямоугольный треугольник SOA вращается вокруг катета SO; при полном обороте гипотенуза AS описывает коническую поверхность, катет OA описывает круг.

Такое тело называется

конусом вращения .

Конусом называется тело, ограниченное замкнутой конической поверхностью и кругом.

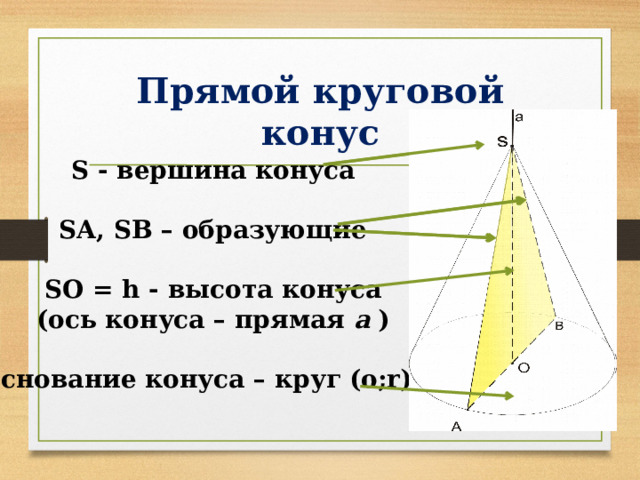
Прямой круговой конус

S - вершина конуса

SA, SB – образующие

SO = h - высота конуса

(ось конуса – прямая а )

Основание конуса – круг (о;r)

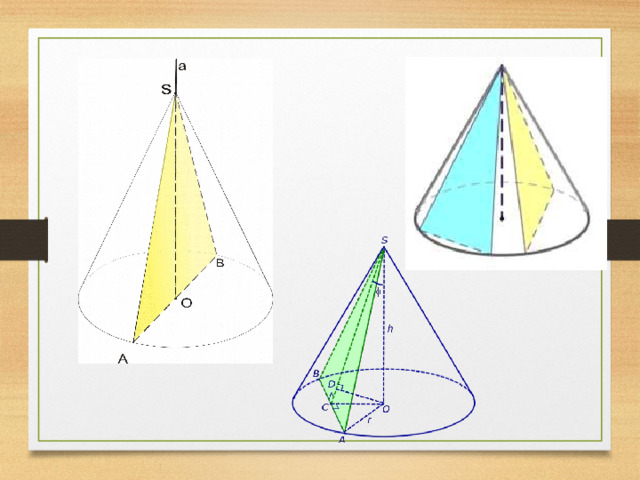
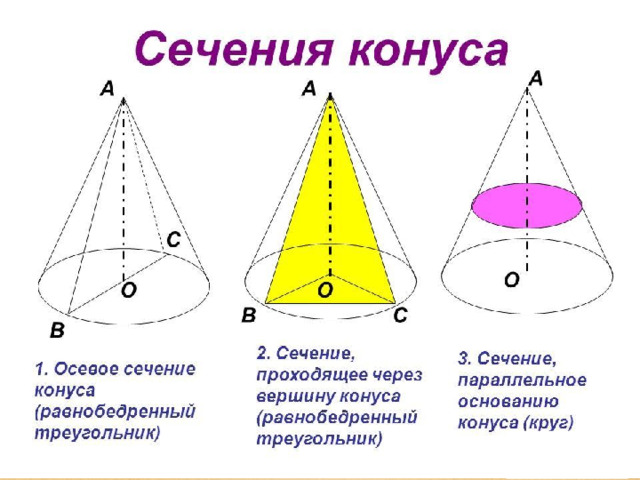
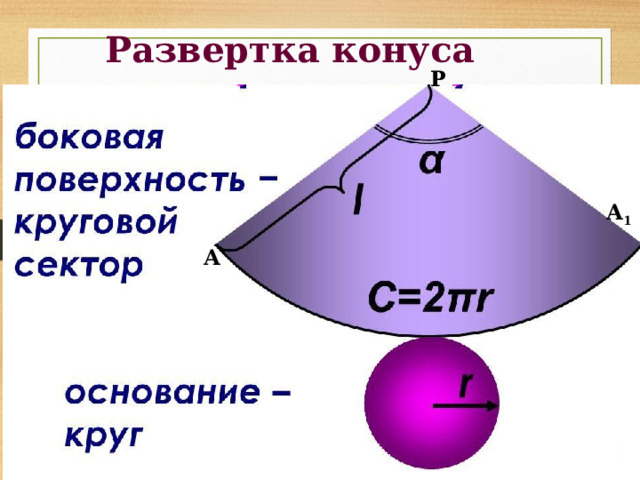
Развертка конуса

Р

А 1

А

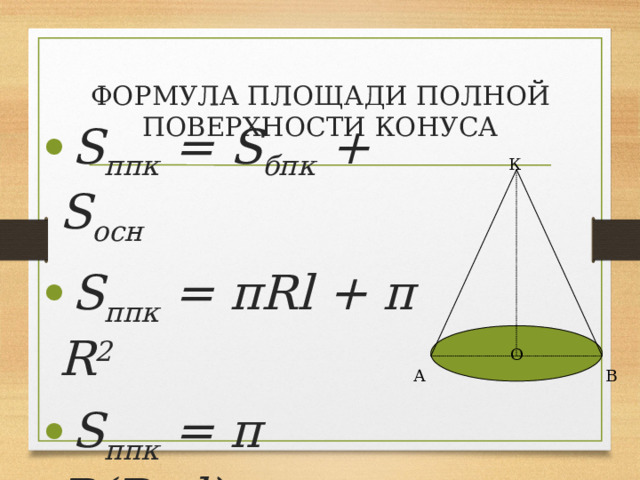
ФОРМУЛА ПЛОЩАДИ ПОЛНОЙ ПОВЕРХНОСТИ КОНУСА

• S ппк = S бпк + S осн
• S ппк = πRl + π R 2
• S ппк = π R(R+l)

К

О

А

В

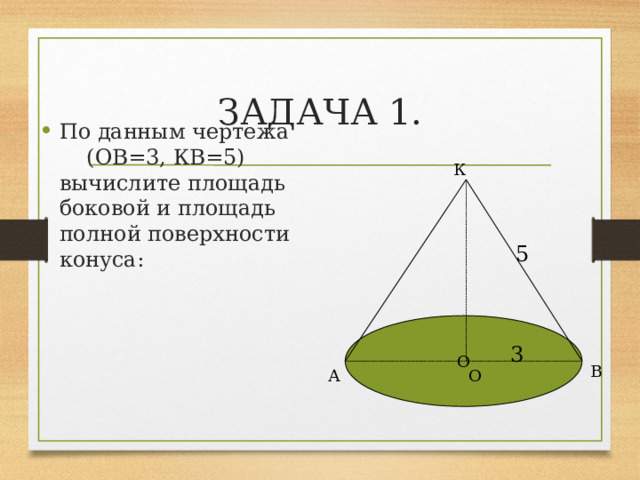
ЗАДАЧА 1.

• По данным чертежа (ОВ=3, КВ=5) вычислите площадь боковой и площадь полной поверхности конуса:

К

5

О

3

В

А

О

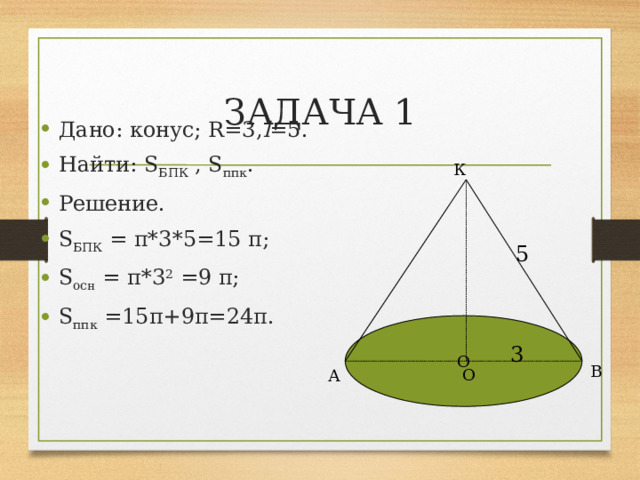
ЗАДАЧА 1

• Дано: конус; R=3, l =5.
• Найти: S БПК , S ппк .
• Решение.
• S БПК = π*3*5=15 π;
• S осн = π*3 2 =9 π;
• S ппк =15π+9π=24π.

К

5

О

3

В

О

А

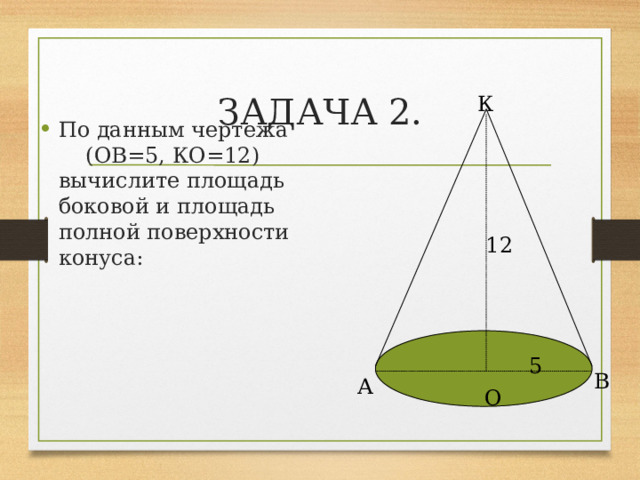
ЗАДАЧА 2.

К

• По данным чертежа (ОВ=5, КО=12) вычислите площадь боковой и площадь полной поверхности конуса:

12

5

В

А

О

ЗАДАЧА 2.

К

• Дано: конус; R=5, h =12.
• Найти: S БПК , S ппк .
• Решение.
• l 2 = 144+25=169 , l= 13;
• S БПК =π*13*5=65 π;
• Sосн = π*5 2 =25 π;
• Sппк =65π+25π;
• Sппк =90π.

12

5

В

А

О

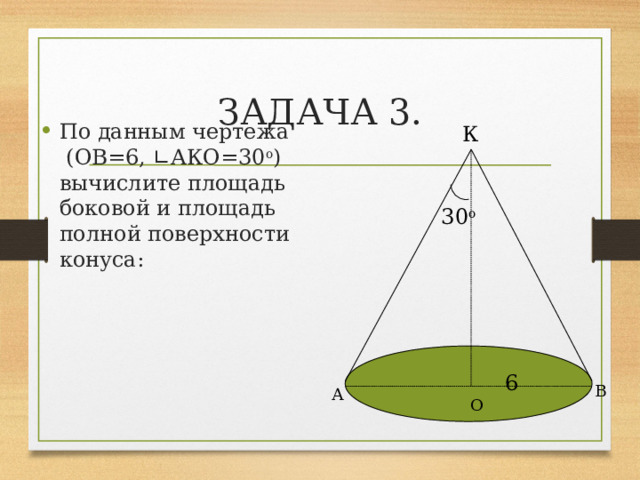
ЗАДАЧА 3.

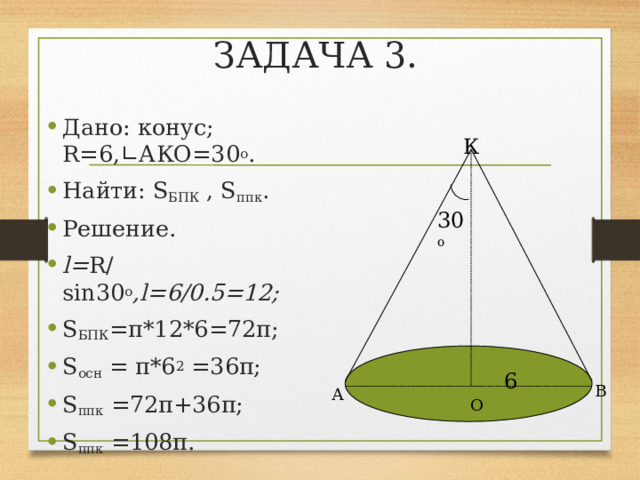
• По данным чертежа (ОВ=6, ∟АКО=30 о ) вычислите площадь боковой и площадь полной поверхности конуса:

К

30 о

6

В

А

О

ЗАДАЧА 3.

• Дано: конус; R=6,∟АКО=30 о .
• Найти: S БПК , S ппк .
• Решение.
• l= R/sin30 о ,l=6/0.5=12;
• S БПК =π*12*6=72π;
• S осн = π*6 2 =36π;
• S ппк =72π+36π;
• S ппк =108π.

К

30 о

6

В

А

О

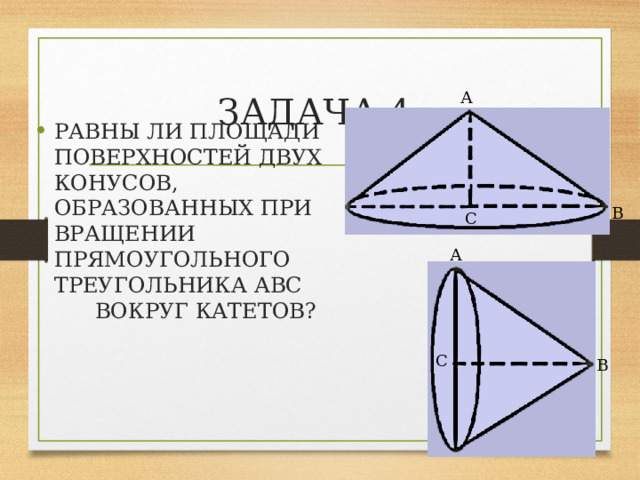
ЗАДАЧА 4.

А

• РАВНЫ ЛИ ПЛОЩАДИ ПОВЕРХНОСТЕЙ ДВУХ КОНУСОВ, ОБРАЗОВАННЫХ ПРИ ВРАЩЕНИИ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА АВС ВОКРУГ КАТЕТОВ?

С

В

С

А

С

С

В

РЕШЕНИЕ ЗАДАЧИ 4

• 1) R=ВС = a ; S ППК 1 = S БПК 1 + S осн1 = π a с+π a 2 = π a (a + с).
• 2) R=АС = b ; S ППК 2 = S БПК 2 + S осн2 = π b с+π b 2 = π b (b + с).
• Если S ППК 1 = S ППК 2 , то a 2 +aс = b 2 +bc, a 2 -b 2 +ac - bc=0, (a-b)(a+b+c)=0. Т.к a,b,c – положительные числа (длины сторон треугольника), то равенство верно только в случае, если a = b.