Презентация на тему : Симметрия 8 класс

Геометрия 8 класс.

Выполнила учитель математики

МКОУ Куминская СОШ

Корзюк Надежда Николаевна.

Содержание

• Симметрия
• Осевая симметрия
• Центральная симметрия
• Задачи
• Симметрия в геометрии, архитектуре, природе
• Заключение

определение

• Симметрия (от греч. Symmetria – соразмерность), в широком смысле – неизменность структуры материального объекта относительно его преобразований. Симметрия играет огромную роль в искусстве и архитектуре. Симметрия встречается в природе, в особенности у кристаллов, у растений и животных. Симметрия встретиться и в других разделах математики, например при построении графиков функций.

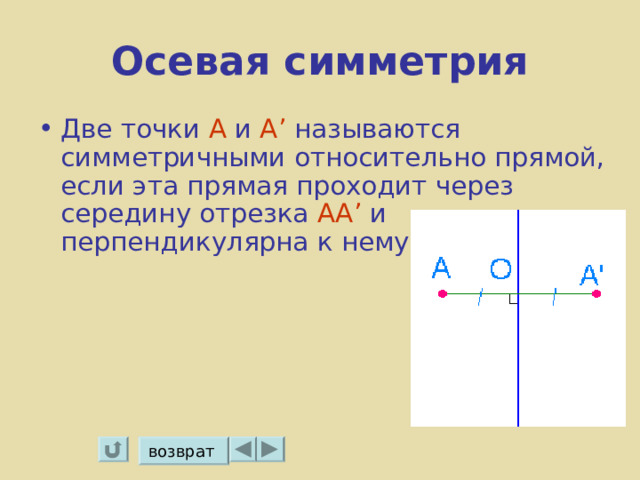
Осевая симметрия

• Две точки А и А ’ называются симметричными относительно прямой, если эта прямая проходит через середину отрезка АА ’ и перпендикулярна к нему.

возврат

• Фигура называется симметричной относительно прямой a , если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре.

а

Центральная симметрия

• Две тоски А и А ’ называются симметричными относительно точки О , если О – середина отрезка АА ’ . Точка О считается симметричной самой себе.

• Фигура называется симметричной относительно точки О , если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре. Точка О называется центром симметрии фигуры.

О

О

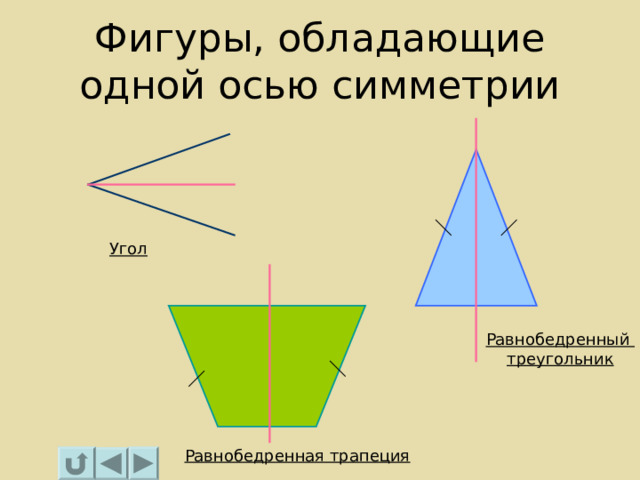
Фигуры, обладающие одной осью симметрии

Угол

Равнобедренный

треугольник

Равнобедренная трапеция

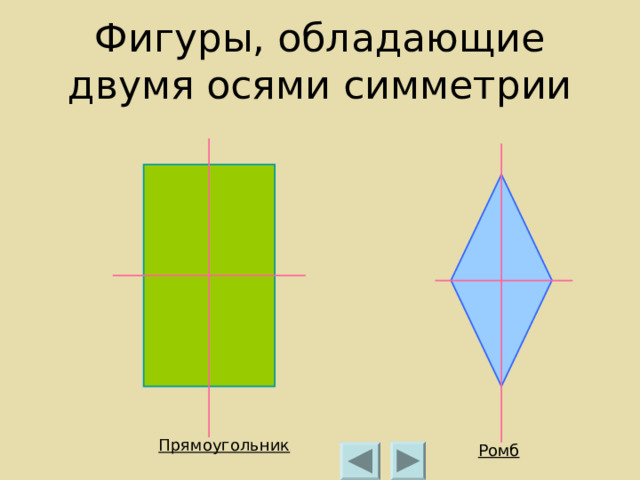
Фигуры, обладающие двумя осями симметрии

Прямоугольник

Ромб

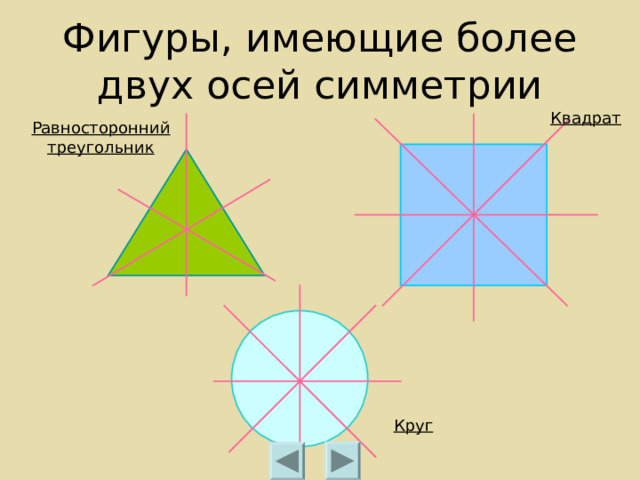
Фигуры, имеющие более двух осей симметрии

Квадрат

Равносторонний треугольник

Круг

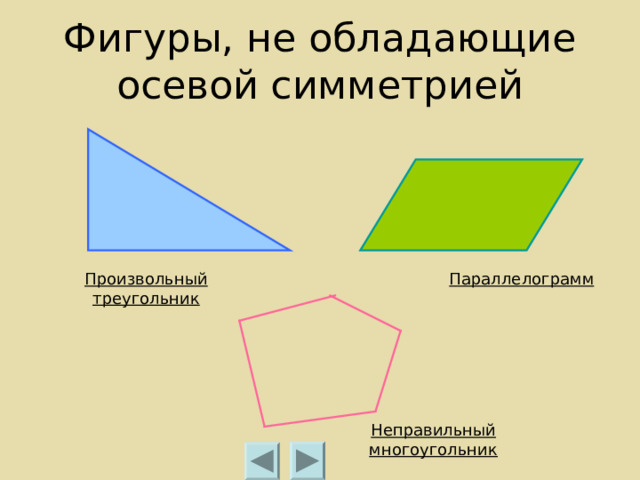
Фигуры, не обладающие осевой симметрией

Произвольный треугольник

Параллелограмм

Неправильный многоугольник

Построение

точки, симметричной данной

отрезка, симметричного данному

треугольника, симметричного данному

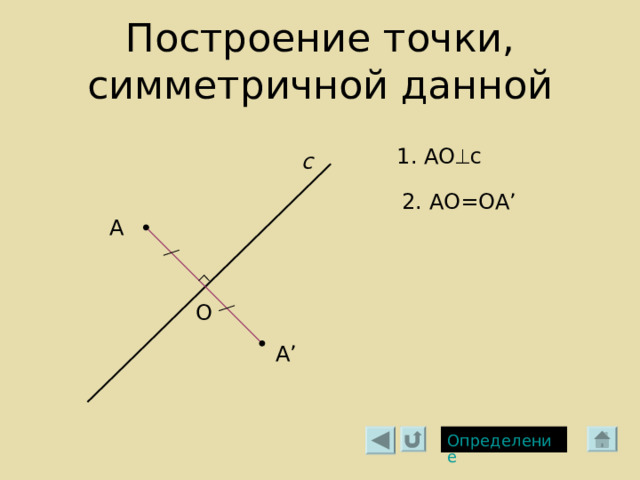
Построение точки, симметричной данной

1 . АО  с

с

2. АО=ОА ’

А

О

А ’

Определение

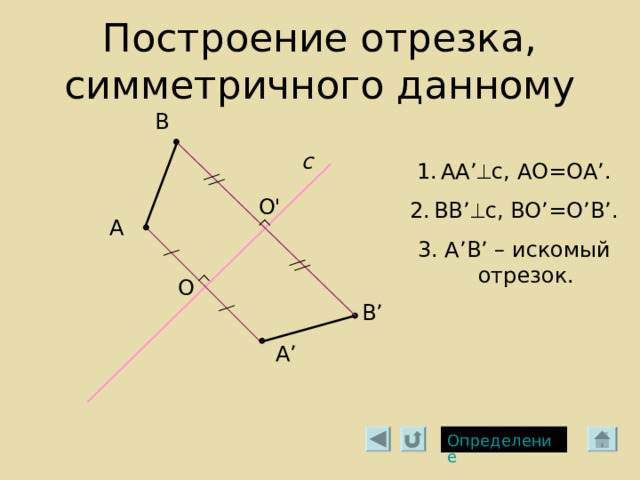
Построение отрезка, симметричного данному

В

с

• АА ’  с, АО=ОА ’ .
• ВВ ’  с, ВО ’ =О ’ В ’ .

3. А ’ В ’ – искомый отрезок.

O'

А

O

В ’

А ’

Определение

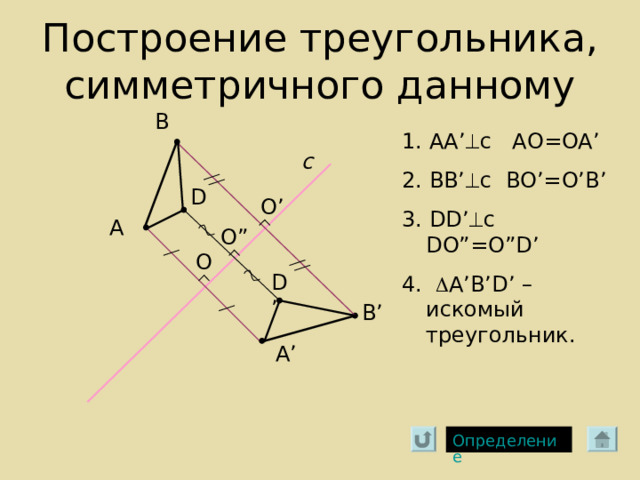
Построение треугольника, симметричного данному

В

1. AA’  c AO=OA’

2. BB’  c BO’=O’B’

3. DD’  c DO”=O”D’

4.  A’B’D’ – искомый треугольник.

с

D

O’

А

O”

O

D’

В ’

А ’

Определение

Задачи

1. Отрезок АВ, перпендикулярный прямой с , пересекает ее в точке О так, что АО≠ОВ. Симметричны ли точки А и В относительно прямой с ?

2. Прямая а пересекает отрезок МК в его середине под углом, отличным от прямого. Симметричны ли точки М и К относительно прямой а ?

3. Точки А и В расположены в различных полуплоскостях с границей р так, что отрезок АВ перпендикулярен прямой р и делится ею пополам. Симметричны ли точки А и В относительно прямой р ?

Задачи

1. Отрезок АВ, перпендикулярный прямой с , пересекает ее в точке О так, что АО≠ОВ. Симметричны ли точки А и В относительно прямой с ?

Ответ: нет

2. Прямая а пересекает отрезок МК в его середине под углом, отличным от прямого. Симметричны ли точки М и К относительно прямой а ?

Ответ: нет

3. Точки А и В расположены в различных полуплоскостях с границей р так, что отрезок АВ перпендикулярен прямой р и делится ею пополам. Симметричны ли точки А и В относительно прямой р ?

Ответ: да

4. Изобразите точку А, лежащую в I четверти

координатной плоскости.

• Точка В симметрична точке А относительно оси y .
• Точка С симметрична точке В относительно оси х.
• Точка D симметрична точке С относительно оси у.

Что вы можете сказать:

• о точках A и D
• о фигуре ABCD
• при каком условии ABCD будет квадратом

Ответ:

• Точки A и D симметричны относительно оси х.
• ABCD – прямоугольник
• Если расстояния от точки А до оси х и у будут равными

возврат

5. Относительно какой из координатных осей симметричны точки М(7;2) и К(-7;2)?

6. Точки А(5;…) и В(…;2) симметричны относительно оси Ох. Запишите их пропущенные координаты.

7. Точка А(-2;3), В - симметричная ей точка относительно оси Ох, точка С – симметричная точке В относительно оси Оу. Найдите координаты точки С.

8. Точка А(3;1), В – симметричная ей точка относительно прямой у = х. Найдите координаты точки В.

• 5. Относительно какой из координатных осей симметричны точки М(7;2) и К(-7;2)? 6. Точки А(5;…) и В(…;2) симметричны относительно оси Ох. Запишите их пропущенные координаты. 7. Точка А(-2;3), В - симметричная ей точка относительно оси Ох, точка С – симметричная точке В относительно оси Оу. Найдите координаты точки С. 8. Точка А(3;1), В – симметричная ей точка относительно прямой у = х. Найдите координаты точки В.
• 5. Относительно какой из координатных осей симметричны точки М(7;2) и К(-7;2)? 6. Точки А(5;…) и В(…;2) симметричны относительно оси Ох. Запишите их пропущенные координаты. 7. Точка А(-2;3), В - симметричная ей точка относительно оси Ох, точка С – симметричная точке В относительно оси Оу. Найдите координаты точки С. 8. Точка А(3;1), В – симметричная ей точка относительно прямой у = х. Найдите координаты точки В.

Проверь себя

Проверь себя

5. Ответ: Оу.

6. Ответ: А(5;-2) и В(5;2).

7. Ответ: С(2;-3).

8. Ответ: В(1;3)

9. Для каждого из случаев, представленных на рисунке, постройте точки А ' и В ' , симметричные точкам А и В относительно прямой с.

А

В

А

В

с

В

А

с

с

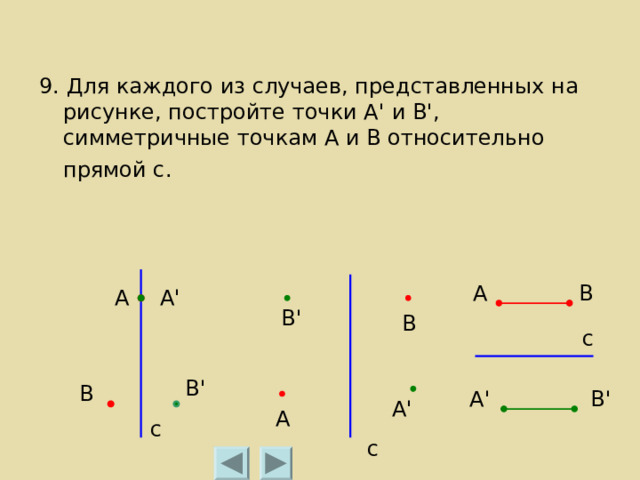
9. Для каждого из случаев, представленных на рисунке, постройте точки А ' и В ' , симметричные точкам А и В относительно прямой с.

В

А

А

А '

В '

В

с

В '

В

В '

А '

А '

А

с

с

10. Постройте треугольники, симметричные данным, относительно прямой с.

с

с

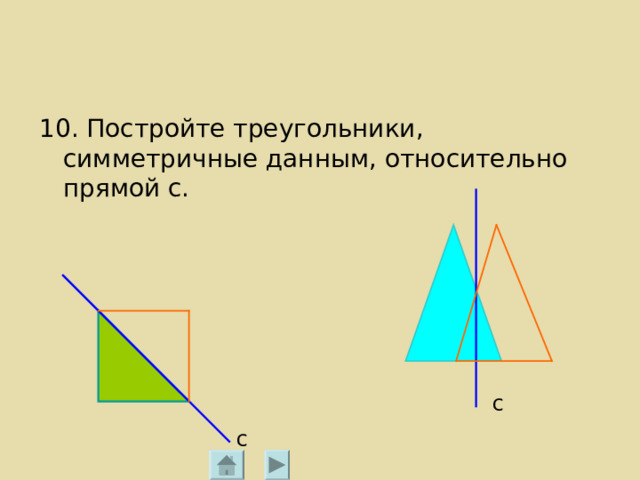
10. Постройте треугольники, симметричные данным, относительно прямой с.

с

с

11. Начертите две прямые а и b и отметьте две точки А и В так, чтобы точка С была симметрична точке А относительно прямой а , а точке В относительно прямой b .

Подсказка

• Для решения задачи рекомендуется сначала отметить точку С, а лишь потом отмечать точки А и В.

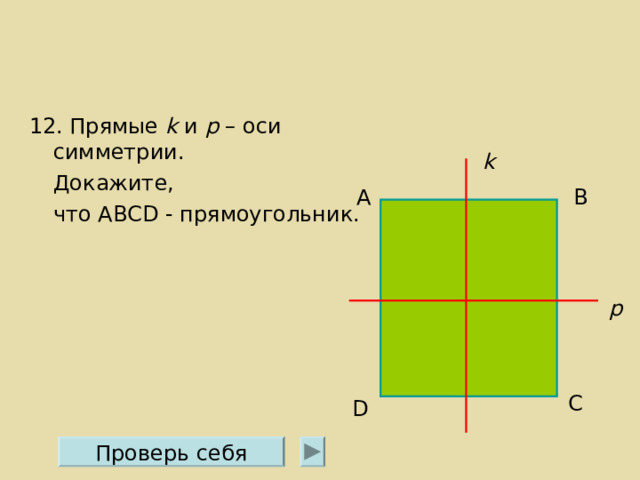
12. Прямые k и р – оси симметрии.

Докажите,

что ABCD - прямоугольник.

k

А

В

р

С

D

Проверь себя

Доказательство:

• Доказательство:
• Доказательство:

Так как k – ось симметрии, то  А=  D ,  В=  С. Так как р – ось симметрии, то  А=  В,  С=  D . Тогда  А=  В=  С=  D =90 ° .

АВС D – прямоугольник.

Симметрия в природе

В архитектуре

Заключение

Симметрию можно обнаружить почти везде, если знать, как ее искать. Многие народы с древнейших времен владели представлением о симметрии в широком смысле – как об уравновешенности и гармонии. Творчество людей во всех своих проявлениях тяготеет к симметрии. Посредством симметрии человек всегда пытался, по словам немецкого математика Германа Вейля, «постичь и создать порядок, красоту и совершенство».