Презентация на тему "Как появилась математика?"

КАКИМИ БЫЛИ ПЕРВЫЕ ЧИСЛА?

• Первые написанные цифры, о которых мы имеем достоверные свидетельства, появились в Египте и Месопотамии около 5000 лет назад. Хотя эти две культуры находились очень далеко одна от другой, их числовые системы очень похожи, как будто представляют один метод: использование засечек на дереве или камне для записи прошедших дней.
• Египетские жрецы писали на папирусе, изготовленном из стеблей определенных сортов тростника, а в Месопотамии – на мягкой глине. Конечно, конкретные формы их цифр были различны, но и в той, и в другой культуре использовали простые черточки для единиц другие метки для десятков и более высоких порядков. Кроме того, в обеих системах писали желаемую цифру, повторяя черточки и метки необходимое число раз.

САМЫЕ ДРЕВНИЕ МАТЕМАТИЧЕСКИЕ ДОКУМЕНТЫ

Найдены два египетских документа, созданных около четырёх тысяч назад, с самыми древними математическими записями из обнаруженных до сих пор.

В них изложены знания древних египтян в области арифметики и геометрии. В этих записях воспроизводятся таблицы умножения, меры площади и объёмов, а также математические задачи и их решения.

КАКИЕ ЦИФРЫ ИСПОЛЬЗОВАЛИ В МЕСОПОТАМИИ .

• Первые образцы письма появились примерно к третьему тысячелетию до рождества Христова и характеризуются использованием стилизованных символов для представления определенных объектов и идей. Постепенно эти знаки приняли более сложные формы.
• В Месопотамии знак

означал единицу и мог повторяться девять раз для изображения чисел от 1 до 9. Знак означал число10 и мог в сочетании с единицами изображать числа от 11 до 59.

• Для изображения числа 60 использовали знак единицы, но в другом положении. Для цифр более 70 использовали знаки, упоминаемые выше, в различных комбинациях.
• В старых вавилонских текстах, датируемых 1700 годом до н.э., не встречается никакого специального знака, обозначающего ноль, для его обозначения там просто оставляли пустое место, более или менее выделенное.

МЕСОПОТАМИЯ – ЦИВИЛИЗАЦИЯ МЕЖДУРЕЧЬЯ.

• Месопотамия – греческое слово, имеющее значение «между двух рек» и означающее цивилизацию, зародившуюся более пяти тысяч лет назад между реками Тигр и Ефрат на Ближнем Востоке. В этом регионе возникли шумерская и вавилонская, или ассирийская, культуры, имевшие огромное значение в истории человечества и осуществившие большой прогресс в области арифметики, письма и астрономии, а также в технике, поскольку именно в Месопотамии было изобретено колесо.

Табличка с матема-

тическим текстом,

Месопотамия

(1800 год до н.э.)

КАКИМИ БЫЛИ ЕГИПЕТСКИЕ ЦИФРЫ?

• Египтяне писали иероглифами, то есть использовали рисунки для отображения какой-либо идеи или объекта. Эти рисунки изображали элементы флоры и фауны реки Нил и домашнюю утварь.
• Цифры они также писали иероглифами. У египтян были знаки для обозначения чисел от 1 до 10 и специальный иероглиф для обозначения десятков, сотен, тысяч, сотен тысяч, миллионов и десятков миллионов.

ЦИВИЛИЗАЦИЯ ЕГИПТА

• Около пяти тысяч лет назад на севере Африки, на берегах Нила, развивалась великая культура. Египтяне благодаря водам Нила развили очень продуктивное сельское хозяйство, построили крупные города и огромные пирамиды, храмы и пантеоны и оставили многочисленные письмена на камнях. Кроме того, они изобрели папирус и различные системы письма, благодаря которым мы открыли часть их знаний. Также огромен их научный вклад в области медицины, геометрии и арифметики.

КАКОЙ БЫЛА РИМСКАЯ СИСТЕМА ИСЧИСЛЕНИЯ ?

• Древние римляне изобрели систему исчисления, основанную на использовании букв для отображения цифр. Они использовали в своей системе следующие буквы: I . \/. L . С. D . М. Каждая буква имела различное значение, каждая цифра соответствовала номеру положения буквы. Для того чтобы прочесть римскую цифру, следует следовать пяти основным правилам:
• 1. Буквы пишутся слева направо, начиная с самого большого значения. Например, Х\/ (15), DLV (555) , МС LI (1 151 ).
• 2. Буквы I . Х. С. и М. могут повторяться до трех раз подряд, например II(2) , ХХХ(30), СС(200), МССХХХ(1230).
• 3. Буквы V. L. D. Не могут повторяться.
• 4. Цифры 4, 9, 40, 90 и 900 следует писать, комбинируя буквы: IV (4), IX (9), XL (40), XC (90), CD (400) , CM (900) . Например, 48 следует писать XLVIII, 449 – CDXLIX. Обратите внимание, что значение левой буквы уменьшает значение правой.
• 5. Горизонтальная линия над буквой у величивает ее з нач ение в 100 0 ра з. Например, V означает 5000 , CIII 103000 и IXDL 9550.

КАКОЙ БЫЛА СИСТЕМА ИСЧИСЛЕНИЯ В ПЛЕМЕНИ МАЙЯ ?

• В Центральной Америке в первом тысячелетии нашей эры майя писали любое число, используя только три знака: точку, линию и эллипс.
• Точка имела значение единицы, линия означала пять. Комбинация точек и линий служила для написания любого числа до девятнадцати. Эллипс под любым из этих чисел увеличивал его в 20 раз.

КАКОЙ БЫЛА СИСТЕМА ИСЧИСЛЕНИЯ У АЦТЕКОВ?

• Цивилизация ацтеков пользовалась системой исчисления, состоящей только из 4 знаков:
• - точка или кружок для обозначения единицы (1);
• - буква « h » для двадцати (20);
• - перо для цифры 400 (20х20);
• - мешок, наполненный зерном, для 8000 (20х20х20).
• Из-за использования малого числа знаков для написания цифры приходилось повторять много раз один и тот же знак, образуя длинный ряд символов. В документах ацтекских чиновников встречаются счета, в которых указываются результаты описи и подсчетов податей, получаемых ацтеками от покоренных городов. В этих документах можно увидеть длинные ряды знаков, похожие на настоящие иероглифы.

КАКИМИ БЫЛИ КИТАЙСКИЕ ЦИФРЫ?

• Происхождение китайской системы счисления более древнее и определяется между 1500 и 1200 годами до нашей эры.
• В конце XIX века крестьяне, возделывающие свои поля, нашли множество черепашьих панцирей и костей животных, исписанных знаками древней китайской системы исчисления. Крестьяне, не знавшие важности этих рисунков, продали эти кости аптекарю, решившему, что они принадлежали дракону и имеют целебные свойства.
• Много лет спустя в другом регионе Китая появилась новая система исчисления. Потребности торговли, управления и науки потребовали развития нового способа написания цифр. Палочками из слоновой кости или бамбука они обозначали цифры от 1 до 9. Цифры от 1 до 5 они обозначали количеством палочек в зависимости от номера. Так, две палочки соответствовали номеру 2. Чтобы указать цифры от 6 до 9, одна горизонтальная палочка помещалась в верхней части цифры.
• Новая система исчисления была отличительной и позиционной: каждая цифра имела определенное значение согласно месту, занимаемому в ряду, выражавшем число.
• Например, номер 2614 изображали следующим образом: две вертикальных палочки, две палочки в форме «Т», одна вертикальная палочка и четыре вертикальные палочки.

ОТКУДА ПРОИЗОШЛИ ИСПОЛЬЗУЕМЫЕ НАМИ ЦИФРЫ?

• Цифры, или символы наших чисел, имеют арабское происхождение, хотя они были заимствованы арабской культурой в Индии.
• Промежуток между VIII и XIII веками стал одним из самых блестящих периодов в истории науки в мусульманском мире. Мусульмане имели тесные связи как с азиатской, так и европейской культурами, и они могли извлечь из них все самое выдающееся. В Индии они заимствовали систему исчисления и некоторые математические методы.
• Современные цифры (1, 2, 3, 4, …) не совсем точно воспроизводят индийские, поскольку арабы их слегка видоизменили, приспосабливая к своему письму. Но исходя из их влияния и авторитета их культуры, современные числовые символы называют арабскими цифрами.

ФИБОНАЧЧИ

• Фибоначчи (1180-1250), известный также под именем Леонардо де Пиза, был итальянским коммерсантом. В сопровождении отца он путешествовал по северу Африки и Ближнему Востоку. Там он занимался изучением индийской математики и арабской системы исчисления. В 1202 году по возвращении в Пизу он написал книгу, в которой познакомил читателей с арабскими цифрами, нулем и позиционной системой исчисления.

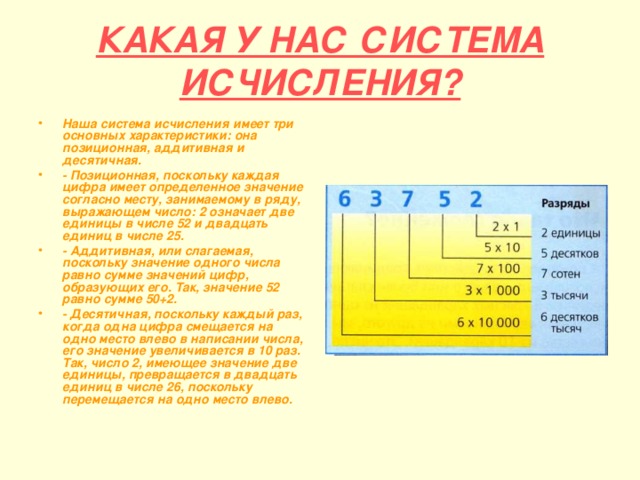
КАКАЯ У НАС СИСТЕМА ИСЧИСЛЕНИЯ?

• Наша система исчисления имеет три основных характеристики: она позиционная, аддитивная и десятичная.
• - Позиционная, поскольку каждая цифра имеет определенное значение согласно месту, занимаемому в ряду, выражающем число: 2 означает две единицы в числе 52 и двадцать единиц в числе 25.
• - Аддитивная, или слагаемая, поскольку значение одного числа равно сумме значений цифр, образующих его. Так, значение 52 равно сумме 50+2.
• - Десятичная, поскольку каждый раз, когда одна цифра смещается на одно место влево в написании числа, его значение увеличивается в 10 раз. Так, число 2, имеющее значение две единицы, превращается в двадцать единиц в числе 26, поскольку перемещается на одно место влево.

КАКИМ БЫЛО ПЕРВОЕ АРИФМЕТИЧЕСКОЕ ДЕЙСТВИЕ?

• Первыми арифметическими действиями были сложение и вычитание. Этими действиями пользовались постоянно в каждодневно жизни. Так добавляли или отнимали определенное количество объектов: «имели 30 овец плюс 4 родились, получилось 34» или «8 коз минус 1 исчезнувшая – получается 7». Для выполнения подобных действий были изобретены простые инструменты, позволяющие складывать и отнимать большие числа. В Европе и Азии использовали счеты, а в Америке инки использовали кипу, делая узелки на разноцветных веревках, которые потом связывали.

КАК ПОЛУЧИТЬ ТАБЛИЦУ СЛОЖЕНИЯ?

• Метод, используемый нами сегодня для сложения, в основном тот же, что и много лет назад. Чтобы получить таблицу сложения, следует начертить сетку с номерами от 0 до 9. В этой таблице можно получить сумму двух номеров. Для этого следует искать результат, следуя по ряду или колонке одного из слагаемых. Результат находится в ячейке пересечения с рядом или колонкой другого слагаемого.

КАК СЧИТАЛИ В ДРЕВНОСТИ КИТАЙЦЫ?

• Для сложения и вычитания китайцы использовали таблицы с колонками. В каждую колонку они вносили цифры, изображенные в виде палочек, соответствующие одному и тому же позиционному значению.

КИТАЙСКОЕ СЛОЖЕНИЕ

Например, сложение 7+8 было выражено

так: первый и второй ряды представляли

7 и 8 соответственно, тогда как третий ряд

отражал их сумму 15.

КИТАЙСКОЕ ВЫЧИТАНИЕ

При вычитании они использовали очень похожую систему. Например, вычитание 15-8 было бы отображено следующим образом: в первом и втором рядах были вписаны 15 и 8

Соответственно, а в третьем ряду результат – остаток 7.

МОЖНО ЛИ ПОМЕНЯТЬ МЕСТАМИ ЧИСЛА ПРИ ВЫЧИТАНИИ?

5 – 4 = 1

4 – 5 = НЕЛЬЗЯ ВЫЧЕСТЬ 5 ИЗ 4.

ОДНАКО

4 – 5 = -1

• Когда мы меняем порядок чисел при вычитании, то это возможно лишь при условии использования отрицательных чисел, то есть меньше нуля.
• Приведем пример: из количества в 8 карандашей можно вычесть 6 и в результате получить 2 карандаша. Но из количества в 6 карандашей мы не можем вычесть 8, так как результат будет меньше нуля, то есть меньше, чем ничего.
• Однако математики используют для обозначения величин меньше нуля знак минус. Поэтому отрицательным числом -1 можно выразить результат вычитания 4-5.

КАК УМНОЖАЛИ В ЖРЕВНЕЙ ИНДИИ?

• В древней Индии применяли два способа умножения: сетки и галеры.
• На первый взгляд они кажутся очень сложными, но если следовать шаг за шагом в предлагаемых упражнениях, это довольно просто.

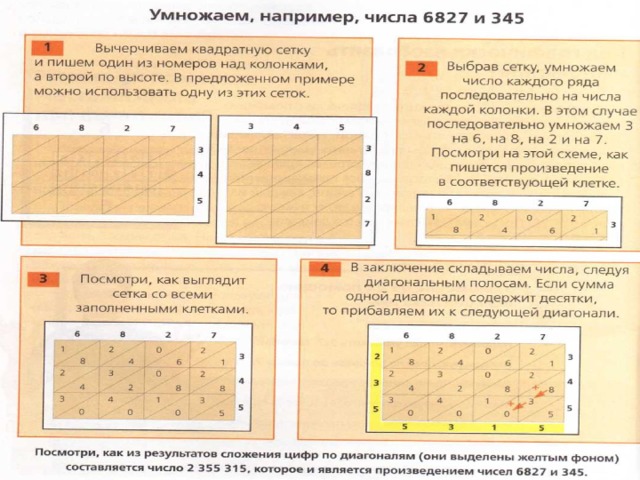
В ЧЕМ СОСТОИТ МЕТОД ГАЛЕРЫ В ИНДИЙСКОМ УМНОЖЕНИИ?

• Для умножения, например, 864 на 248 напишем одно число как множимое и под ним другое как множитель. Чтобы легче ориентироваться. можно использовать сетку (А) как образец.
• Теперь умножаем левую цифру множителя на каждую цифру множимого, то есть, 2х8, 2х6 и 2х4. Полученные произведения пишем в сетку (В), имея в виду следующие правила:
• ПРАВИЛО 1. Единицы первого произведения следует писать в той же колонке, что и множимое, то есть в данном случае под 2.
• ПРАВИЛО 2. последующие произведения надо писать таким образом, чтобы единицы помещались в колонке непосредственно справа от предыдущего произведения.
• Теперь повторим весь процесс с другими цифрами множителя, следуя тем же правилам (С).
• Как можно видеть, мы получаем большой список произведений. Индийцы, имевшие большую практику, писали каждую цифру не в соответствующую колонку, а сверху, насколько это возможно. Затем они складывали цифры в колонках и получали результат ( D ).

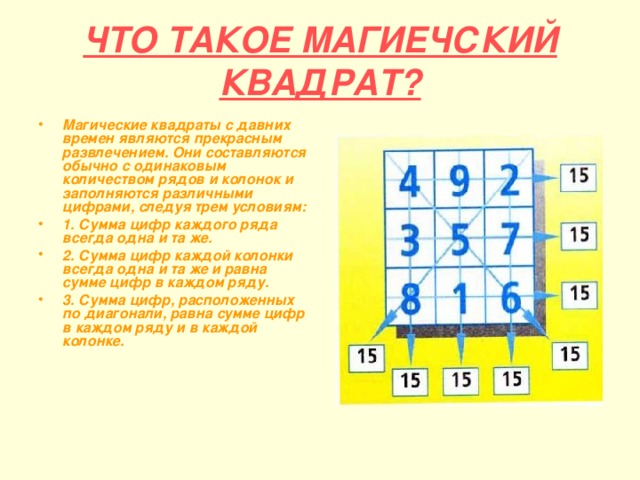
ЧТО ТАКОЕ МАГИЕЧСКИЙ КВАДРАТ?

• Магические квадраты с давних времен являются прекрасным развлечением. Они составляются обычно с одинаковым количеством рядов и колонок и заполняются различными цифрами, следуя трем условиям:
• 1. Сумма цифр каждого ряда всегда одна и та же.
• 2. Сумма цифр каждой колонки всегда одна и та же и равна сумме цифр в каждом ряду.
• 3. Сумма цифр, расположенных по диагонали, равна сумме цифр в каждом ряду и в каждой колонке.

АЛЬБРЕХТ ДЮРЕР

• Альбрехт Дюрер (1471-1528) – известный живописец и график немецкого Возрождения. В одну из своих гравюр, «Меланхолию», он включил магический квадрат. Обратите внимание, что, помимо совпадения сумм в рядах, колонках и диагоналях, совпадают также суммы центрального квадрата и каждого из четырех квадратов, образованных средними линиями.

СУЩЕСТВУЕТ ЛИ ВЗАИМОСВЯЗЬ МЕЖДУ МУЗЫКОЙ И ЧИСЛАМИ?

• В основе музыки лежат мелодия, ритм и гармония. При сочинении мелодии музыканты пишут ноты, имеющие разное значение, то есть каждая нота должна длиться определенное время. Каждая нота имеет свое название согласно своей продолжительности. Самая длинная нота называется целой нотой, за ней следуют половинная, четвертная, или четверть, восьмая, шестнадцатая и другие меньшей продолжительности. Между продолжительностью нот существует взаимосвязь: каждая нота «в два раза более», чем последующая, или составляет «половину» предыдущей. Так, целая нота длится столько же, что и две половинных, а две половинные столько же, что и четыре четвертных, а эти в свою очередь столько же, что восемь восьмушек, а они столько же, что и шестнадцать шестнадцатых, и т.д.
• С другой стороны, ритм, основой которого является четкое следование временным интервалам, как биению сердца, выражается с помощью такта, записывающегося в виде дроби: 2/3, ¾, 4/5, 6/8 … Имеется специальный инструмент, называемый метрономом, служащий для измерения такта, чтобы не потерять ритм.