Презентация к уроку: "Разность квадратов"

• Изучение формулы разности квадратов
• Применение формулы для рационализации вычислений

• Что называется квадратом числа?

a² = a*a

• 1. Вычислить : 2² 8²

3² 10²

5² 11²

• 2. Возведите в степень (2ав)²
• ( - 7с³ d)²
• ( - а²в³с)²
• ( 0,1 а²в³с)²
• ( - 3ху²)²

Что называется многочленом?

Как умножить один многочлен на другой?

• 1. (a + b) (c + d)
• 2. (x + y) (x – 2)
• 3. (х +2)(х -3)
• 4. (2у +1)(у - 4)

• 1. xy + 2y
• 2. x² - xy
• 3. ad² + ad
• 4. a² - b²
• 5. x² - 4

• 1. (х - 3)(х + 3)
• 2. (а + 4)(а -4)
• 3. (у +6)(у – 6)
• 4. (а +1)(а – 1)
• 5. (х -5)(х+5)

• 1. х² -9 2. а² -16 3. у² – 36 4. а² -1 5. х² -25
• 1. х² -9 2. а² -16 3. у² – 36 4. а² -1 5. х² -25
• 1. х² -9
• 2. а² -16
• 3. у² – 36
• 4. а² -1
• 5. х² -25

• (х - 3)(х + 3)= х² -9
• (а + 4)(а -4)= а² -16
• (у +6)(у – 6)= у² – 36
• (а +1)(а – 1)= а² -1
• (х -5)(х+5)= х² -25

• (у + 2)(у – 2)=
• (х +10)(х -10)=
• (а +7)(а – 7)=

• у ² – 4
• х ² – 100
• а ² - 49

Молодцы!

Молодцы! Давайте сделаем вывод, для этого попробуем вывести формулу

(а +в)(а – в)=…

(а + в)(а – в) = а² - в²

Запомни!

Теперь попробуем сформулировать правило.

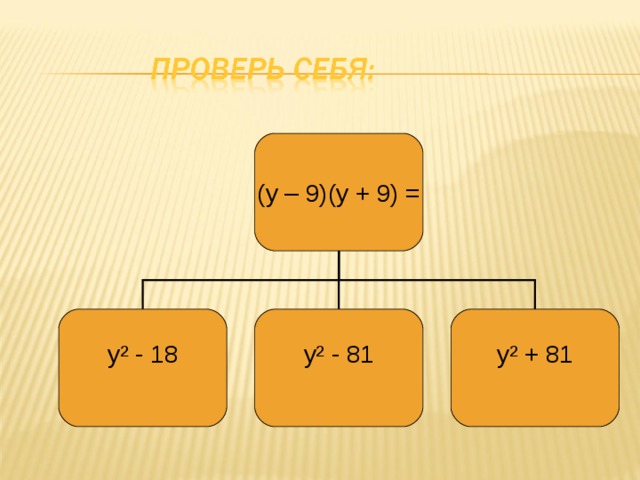
(у – 9)(у + 9) =

у² - 81

у² + 81

у² - 18

Твои ответы:

4-х ²

х²-4

х²-4

4-х ²

4-х ²

х²-4

Решим примеры сложнее,

(2-х)(2+х)

(-2+х)(2+х)

(х-2)(2+х)

(х+2)(2-х)

(2-х)(х+2)

(-2-х)(2-х)

(а – в)(а + в) = а² - в²

Попробуй решить эти примеры устно.

69 · 71

31· 29

89 · 91

99 · 101

(а – в)(а + в) = а² - в²

69 · 71 =

= (70 – 1) (70 + 1) = 70² - 1² = 4900 – 1 = 4899

31· 29 = 899

89 · 91 = 8099

99 · 101 = 9999

Выполни упражнения из учебника

№ 356 (1,3)

№ 357 (1,3)

№ 358 (1,3)

№ 359

Выучи формулу, правило и выполни упражнения из учебника: пар.21

№ 356 (2,4)

№ 357 (2,4)

№ 358 (2,4)

№ 360