Презентация к уроку математики 5 класс "Комбинаторные задачи"

Комбинаторные задачи

УМК: А.Г. Мерзляк и др.

5 класс

Разработано учителем математики МБОУ - Полужская ООШ им.Ф.Е.Стрельца.

Басовой Е.В.

2020 г.

Прозвенел уже звонок,

Встали тихо, замолчали,

Всё, что нужно, вы достали.

Приготовились к уроку,

В нём иначе нету проку.

Здравствуйте, садитесь,

Больше не вертитесь.

Мы урок начнем сейчас,

Интересен он для вас.

Слушай всё внимательно,

Поймешь всё обязательно.

Математика уступает свои крепости лишь сильным и смелым.

(А.П. Конфорович)

Какой рисунок солнышка соответствует твоему настроению на начало урока

3

1

2

Повторение

1. Чему равен объём куба, ребро которого равно 8 дм?

2. Чему равен объём прямоугольного параллелепипеда с с измерениями и 2см, 6 см и 10 см?

3.Вычислите сумму

27 + 16 + 33 + 24.

4. Из цифр 7, 4, 5 составили трёхзначные числа. Сколько чисел получится и какие это числа, если цифры не повторяются?

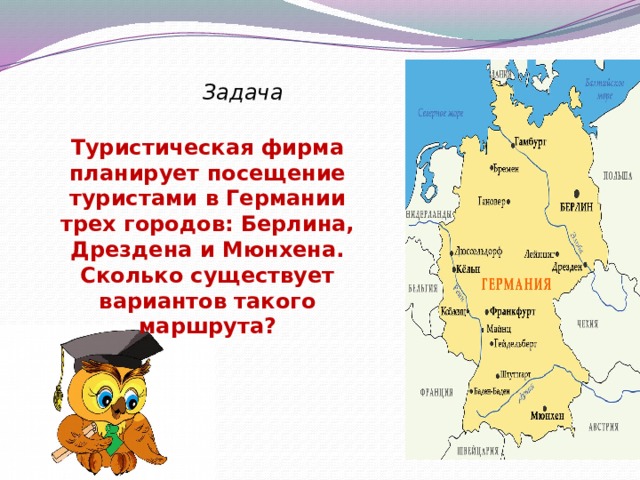
Задача

Туристическая фирма планирует посещение туристами в Германии трех городов: Берлина, Дрездена и Мюнхена. Сколько существует вариантов такого маршрута?

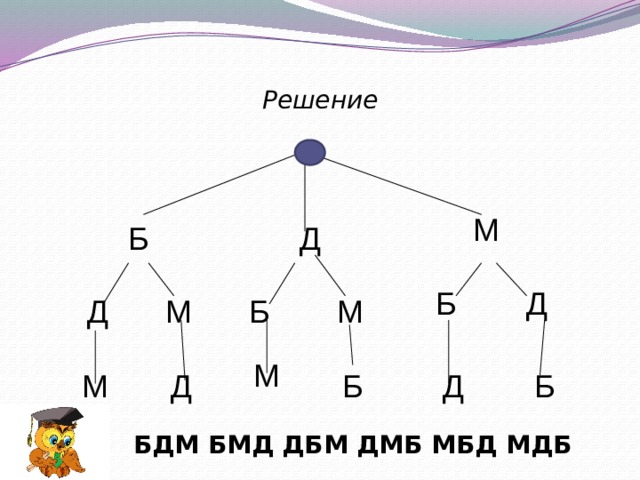
Решение

М

Д

Б

Д

Б

М

Б

М

Д

М

Д

М

Б

Б

Д

БДМ БМД ДБМ ДМБ МБД МДБ

Нередко в повседневной жизни мы встречаемся с задачами, решение которых требует рассмотрения всех возможных случаев, или, как ещё принято говорить, всех возможных комбинаций . Поэтому такие задачи называют комбинаторными

Комбинаторные

задачи

Слово «комбинаторика» происходит от латинского слова «combinare», что в переводе на русский означает – «сочетать», «соединять».

Термин "комбинаторика" был введён знаменитым Готфридом Вильгельмом Лейбницем, - всемирно известным немецким учёным.

Занимался идеями комбинаторного искусства.

Комбинаторика   - раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчинённых тем или иным условиям, можно составить.

Методы решения комбинаторных задач

- Метод перебора вариантов:

если нужных комбинаций не слишком много, то все их можно просто

Перечислить, или, как говорят перебрать все возможности.

-Изображение дерева возможных вариантов: позволяет наглядно представить

все варианты.

• Правило умножения:
• Применяется, когда количество возможных вариантов достаточно велико.

Задача № 1

В 5 классе в пятницу 3 урока: математика, литература, родной язык. Сколько вариантов расписания можно составить?

Задача №2

У Арсения есть три книги: красная, зелёная и фиолетовая. Сколько существует способов расставить эти книги на полку?

Задача № 3

Сколько различных трёхзначных чисел можно составить из цифр 1, 3, 5? (Цифры НЕ могут повторяться!)

Задача № 4

Сколько различных трёхзначных чисел можно составить из цифр 2, 4, 6? (Цифры НЕ могут повторяться!)

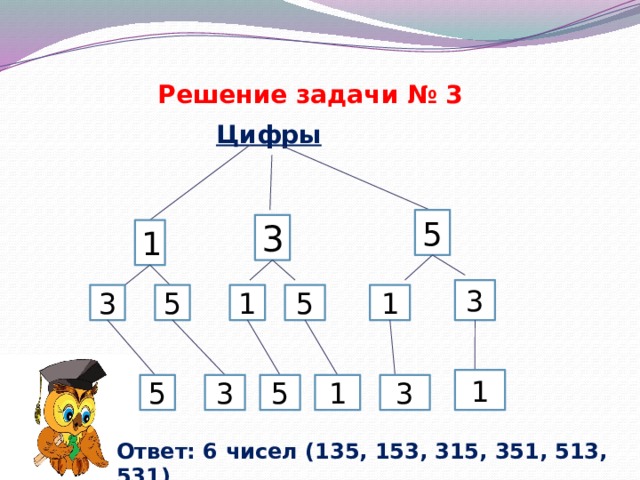
Решение задачи № 3

Цифры

5

3

1

3

5

1

1

5

3

1

5

1

3

5

3

Ответ: 6 чисел (135, 153, 315, 351, 513, 531)

Физкультминутка

• Потрудились – отдохнем.
• Встанем, глубоко вздохнем.
• Руки в стороны, вперед,
• Влево, вправо поворот.
• Три наклона, прямо встать,
• Руки вниз и вверх поднять.
• Руки плавно опустили,
• Всем улыбки подарили .

Задача № 5

Сколько различных завтраков, состоящих из 1 напитка и 1 вида выпечки, можно составить из чая, кофе, бутерброда, печенья и вафель?

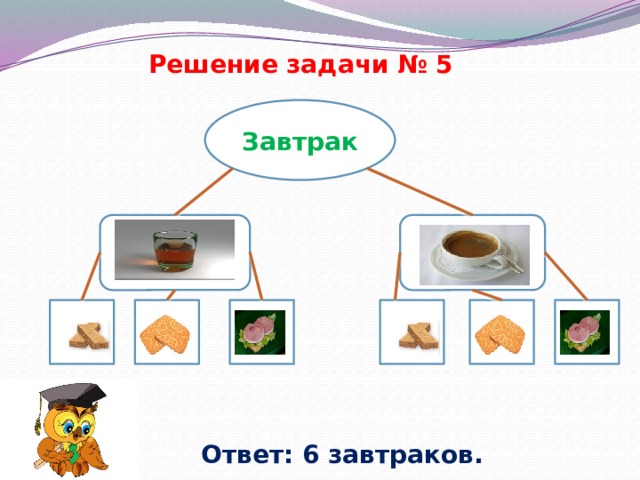
Решение задачи № 5

Завтрак

Ответ: 6 завтраков.

Задача № 6

У ослика Иа-Иа есть три надувных шарика: красный, зелёный и жёлтый. Он хочет подарить их Винни-Пуху, Пятачку и Кролику. Сколько у ослика есть вариантов сделать подарки своим друзьям?

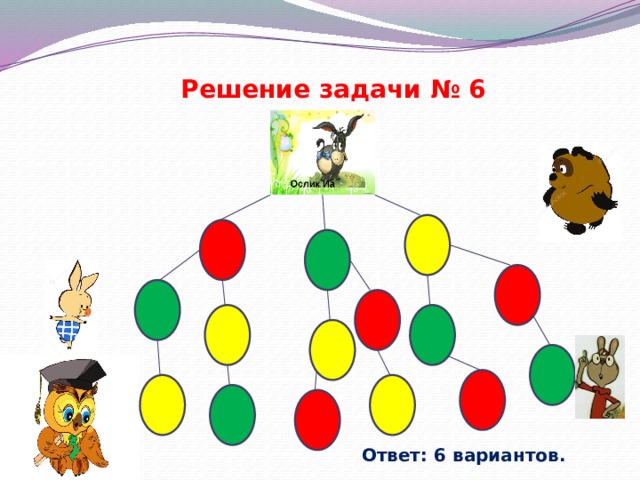
Решение задачи № 6

Ответ: 6 вариантов.

Проблемный вопрос:

Может ли нам комбинаторика помочь в реальной жизни?

Области

применения

комбинаторики:

ГИА

Домашнее задание

Прочитать параграф 24(стр.160-163)

№ 646, 648,652, 662, 4(стр163)

Рефлексия

Мне было интересно. Я доволен своей работой на уроке

На уроке я работал неплохо, но не всё было понятно

На уроке мне было трудно