Элементы комбинаторики, теории вероятностей и логики на уроках математики

Презентация к уроку математики в 5 классе дает представление о решении комбинаторных задач деревом возможных вариантов и по правилу произведения. Подборка задач позволит учащимся решать подобные задания устно. теория вероятности представлена событиями, изучая которые учащиеся учатся различать невозможные, достоверные и случайные события. Для решения логических задач на уроке предусмотрен тренажер "решение логических задач."

Элементы комбинаторики, теории вероятностей и логики на уроках математики

Учитель математики

МОУ СОШ № 20

Суворова Л.В.

п. Железнодорожный

2008 г.

раздел математики, в котором исследуются задачи выбора элементов из исходного конечного множества и способы расположения их в некоторой комбинации.

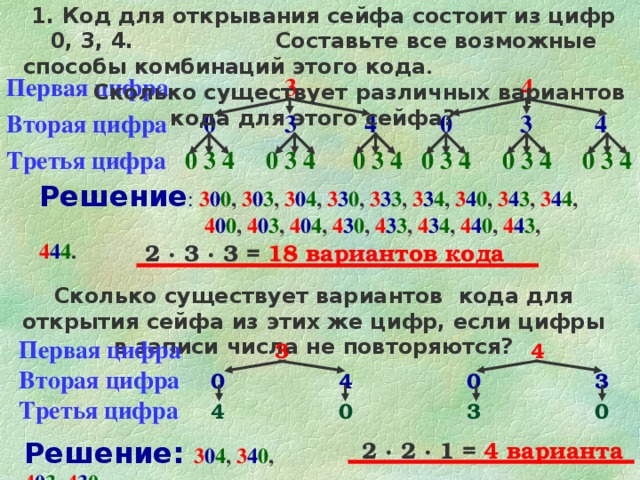
1. Код для открывания сейфа состоит из цифр 0, 3, 4. Составьте все возможные способы комбинаций этого кода . Сколько существует различных вариантов кода для этого сейфа?

Первая цифра

Вторая цифра

3

Третья цифра

0 3 4

4

0 3 4 0 3 4 0 3 4

0 3 4

0 3 4 0 3 4 0 3 4

Решение : 3 0 0 , 3 0 3 , 3 0 4 , 3 3 0 , 3 3 3 , 3 3 4 , 3 4 0 , 3 4 3 , 3 4 4 , 4 0 0 , 4 0 3 , 4 0 4 , 4 3 0 , 4 3 3 , 4 3 4 , 4 4 0 , 4 4 3 , 4 4 4 .

2 · 3 · 3 = 18 вариантов кода

Сколько существует вариантов кода для открытия сейфа из этих же цифр, если цифры в записи числа не повторяются?

Первая цифра 3 4

Вторая цифра 0 4 0 3

Третья цифра 4 0 3 0

Решение: 3 0 4 , 3 4 0 , 4 0 3 , 4 3 0 .

2 · 2 · 1 = 4 варианта

2. Сколько трехзначных чисел можно составить из цифр 1, 3, 5?

Решение: 3 · 3 · 3 = 27 чисел

3. Сколько четырехзначных чисел, в которых цифры не повторяются, можно составить из цифр 0, 2, 4, 6?

Решение : 3 · 3 · 2 · 1 = 18 чисел

4. В кафе имеются три первых блюда, пять вторых блюд и два третьих. Сколькими способами можно заказать обед, состоящий из первого, второго и третьего блюд?

Решение: 3 · 5 · 2 = 30 способов

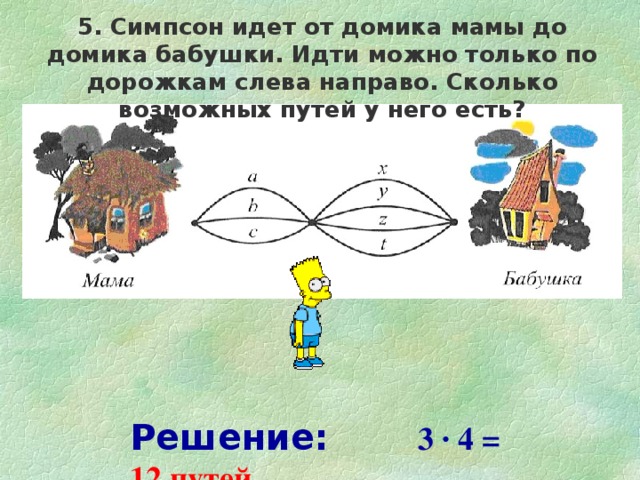
5. Симпсон идет от домика мамы до домика бабушки. Идти можно только по дорожкам слева направо. Сколько возможных путей у него есть?

Решение: 3 · 4 = 12 путей

6. В футбольной команде 5 класса 11 человек. Сколькими способами можно выбрать капитана и вратаря команды?

Решение: 11 · 10 = 110 способов

7. Сколькими способами можно разместить 4 кролика в клетке, состоящей из четырех отделов?

Решение: 4 · 3 · 2 · 1 = 24 способа

Событие – любое явление, которое происходит или не происходит. Событиями являются результаты испытаний (опытов), наблюдений и измерений.

Невозможное событие – в данных условиях произойти не может.

30 февраля

Достоверное событие – в данных условиях обязательно произойдет.

31 декабря

Случайное событие – в данных условиях может произойти, а может и не произойти.

СПАСИБО ЗА УРОК!