Презентация "Интегралы"

ИНТЕГРАЛЫ

Что такое интеграл?

Интеграл - одно из наиболее важных и распространенных понятий в высшей математике, которое появилось из-за необходимости измерять объёмы, площади, работу нескольких сил за конкретный промежуток времени, длины дуг и т.д. Термин «интеграл» (от лат. integer — целый, то есть целая, вся — площадь) был предложен в 1696 г. Иоганном Бернулли. 

Ученый, создавший интеграл

Евдокс Книдский (ок. 408-355 гг. до н.э.) – древнегреческий учёный. Дал полное доказательство теоремы об объёме пирамиды; теоремы о том, что площади двух кругов относятся как квадраты их радиусов. При доказательстве он применил так называемый метод «исчерпывания», который нашёл своё использование (с некоторыми изменениями) в трудах его последователей. Через две тысячи лет метод «исчерпывания» был преобразован в метод интегрирования, с помощью которого удалось объединить самые разные задачи – вычисление площади, объёма, массы, работы, давления, электрического заряда, светового потока и многие, многие другие.

Вслед за Евдоксом метод «исчерпывания» и его варианты для вычисления объёмов и площадей применял древний учёный Архимед . Успешно развивая идеи своих предшественников, он определил длину окружности, площадь круга, объём и поверхность шара. Он показал, что определение объёмов шара, эллипсоида, гиперболоида и параболоида вращения сводится к определению объёма цилиндра. Выражаясь современным языком, Архимед определил интегралы

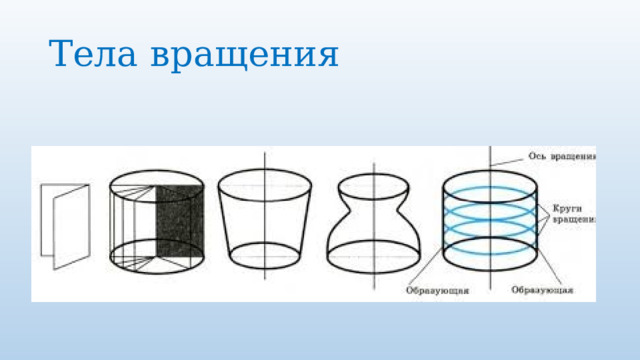
Тела вращения

Иллюстрация интегрирования

Предположим, что нам надо вычислить объём лимона, имеющего неправильную форму, и поэтому применить какую-либо известную формулу объёма нельзя. С помощью взвешивания найти объём также трудно, так как плотность лимона в разных частях его разная. Поступим следующим образом.

Разрежем лимон на тонкие дольки. Каждую дольку приближённо можно считать цилиндриком, радиус основания, которого можно измерить. Объём такого цилиндра вычислить легко по готовой формуле. Сложив объёмы маленьких цилиндров, мы получим приближенное значение объёма всего лимона. Приближение будет тем точнее, чем на более тонкие части мы сможем разрезать лимон.

Развитие понятия интеграла

Первые значительные попытки развития интеграционных методов Архимеда, увенчавшиеся успехом, были предприняты в XVII в., когда, с одной стороны, были достигнуты значительные успехи в области алгебры, а с другой – все более интенсивно развивались экономика, естествознание и техника, требовавшие более общих и мощных математических методов изучения и вычисления величин .

Одним из первых видных ученых XVII в., стремившихся к возрождению и развитию интеграционных метода Архимеда, был Иоганн Кеплер (1571-1630), открывший законы движения планет. Кеплер вычислял площади плоских фигур и поверхностей , объемы тел, основываясь на идее разложения фигур и тел на бесконечное число бесконечно малых частей, которые он называл «тончайшими кружочками» или «частями крайней малой ширины»; из этих мельчайших частиц, суммированных им, он составляет фигуру, эквивалентную первоначальной, но площадь или объем которой ему известен.

1612 г. был для жителей австрийского города Линца, в котором жил тогда Кеплер, и его окрестностей исключительно урожайным, особенно изобиловал виноград. Люди заготовляли винные бочки и хотели знать, как практически определять их объемы. Этот вопрос как раз и входил в круг идей, которыми интересовался Кеплер. Так родилась его «Новая стереометрия винных бочек», вышедшая в свет в 1615г.

Самыми видными учеными, подготавливавшими в XVII в., создание интегрального и дифференциального исчисления, завершенное Ньютоном и Лейбницем, были Дж. Валлис., П. Ферма и Б. Паскаль.

П. Ферма (1601-1665).

Он впервые разбил фигуру

под кривой на малые полоски,

которые можно принять

за прямоугольники.

Ньютон к основным понятиям и к алгоритму исчисления бесконечно малых пришел в середине 60-х годов XVII в., когда двадцатилетний Лейбниц был студентом юридического факультета и математикой еще не занимался.

1646-1716 1643-1727

Ньютон и Лейбниц, самостоятельно, каждый своими математическими выкладками пришли к понятию определенного интеграла и вывели формулу Это и есть так называемая теперь «Формула Ньютона - Лейбница», которая носит название «основной формулы интегрального исчисления». Она позволяет сводить довольно сложное вычисление определенных интегралов, т.е. нахождение предела интегральных сумм, к сравнительно более простой операции отыскивания первообразных.

Обозначение

Современное обозначение неопределенного интеграла было введено Лейбницем в 1675 году. Он адаптировал интегральный символ , образованный из буквы S — сокращения слова лат.  summa (сумма).

Современное обозначение

определенного интеграла,

с ограничениями над и под

знаком интеграла, были впервые

использованы Жаном Батистом Жозефом Фурье в 1819-20.

Формула Ньютона-Лейбница

Бернхард Риман формализовал понятие интеграла, разработанное Ньютоном и Лейбницем, как площади подграфика (фигуры, заключенной между графиком функции и осью абсцисс).

Для этого он рассмотрел фигуры, состоящие из некоторого количества вертикальных прямоугольников, основания которых составляют вместе отрезок интегрирования и получаются при разбиении отрезка (см. рисунки) на соответствующее количество маленьких отрезков. Площадь S такой фигуры при конкретном разбиении на отрезки длинами Δ x i будет интегральной суммой

Разные интегралы

Одно из главных правил интегрального исчисления определяет, что любая непрерывная функция f(x) имеет неопределённый интеграл.

Жан Гастон Дарбу (1842-1917)

Интеграл Лебега – это обобщение интеграла Римана на более широкий класс функций. Идея интеграла Лебега состоит в том, что вместо разбиения на части по оси Х разбивают интервалы по оси У, что позволяет находить интегралы для объектов, имеющих разную плотность, разрывы, вообще для неоднородных объектов.

Сверху интегрирование по Риману,

снизу по Лебегу

Анри Леон Лебег

1875-1941

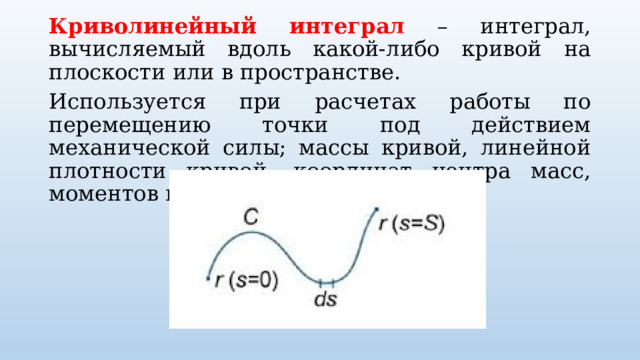
Криволинейный интеграл – интеграл, вычисляемый вдоль какой-либо кривой на плоскости или в пространстве.

Используется при расчетах работы по перемещению точки под действием механической силы; массы кривой, линейной плотности кривой, координат центра масс, моментов инерции кривой.

Двойные и тройные интегралы

Кратные интегралы «устроены» принципиально так же, как обычные, они отличаются только областью интегрирования: у двойных интегралов– это не отрезок, а плоская фигура, у тройных - пространственное тело.

Геометрический смысл двойного интеграла

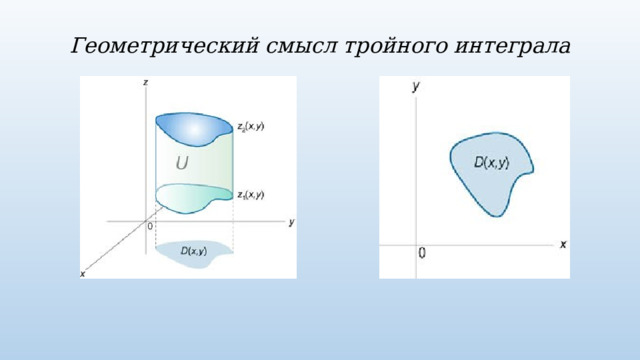
Геометрический смысл тройного интеграла

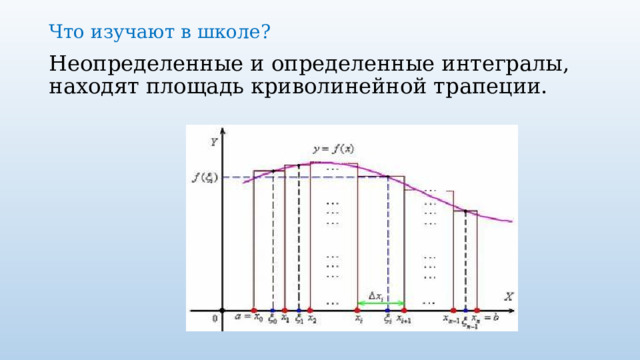
Что изучают в школе?

Неопределенные и определенные интегралы, находят площадь криволинейной трапеции.

Классическая схема интегрального исчисления

– отрезок  [a; b] дробится на части; – составляется интегральная сумма, которая равна площади ступенчатой фигуры; – и, наконец, количество отрезков разбиения устремляется к бесконечности – в результате чего эта фигура превращается в криволинейную трапецию площади